2.武汉大学资源与环境科学学院,湖北武汉430079
2.School of Resources and Environment Science,Wuhan University,Wuhan 430079, China
1 引言
随着城市化发展和人口的增加,人地矛盾日益突出,土地资源的立体化利用成为破解这一矛盾的有效手段。《物权法》规定土地使用权可以在地表、地上、地下分别设立,为土地的立体化应用提供了法律保障。立体化利用对传统的二维地籍形成挑战,必须将二维宗地拓展为三维产权体,构建三维地籍。三维产权体是封闭的真三维几何体,通过土地管理过程中基于测量的界址点、线和面来表达。因此,三维地籍中的一个核心问题是以点、线、面为基础数据,构建具有完全拓扑关系的三维数据模型,以表达三维地籍产权体及其相互关系,实现对其进行高效管理。
当前3D GIS的研究主要包括三维模型的拓扑分析[1, 2]和“数字城市”,后者往往侧重于其对城市景观逼真的视觉表现,重视外在表面的可视化表达,还没有触及地籍和房产单元。目前三维城市建模的研究,一方面多集中在三维建筑模型的创建,或者如何加工生产三维数据方面,如基于体和影像方法的城市三维建筑物建模[3, 4]、矢量拔高生成建筑物模型[5, 6, 7, 8],该类方法有两个弱点:① 多要求底面和顶面图形完全相同,且相互平行,侧立面必须垂直于底面和顶面;②虽称之为三维模型,但该模型仅具有三维空间坐标,本质上该模型还是离散的面片,不具有严格的几何和拓扑上三维体的概念,同时也缺乏体和面片的组织关系,三维体的空间关系亦无从谈起,更无法论及三维体的计算及相关分析。另一方面,现在的3D系统并不能真正地识别三维对象,因为它们没有真正的三维体要素来模型化[9]。因此无法真正地做到三维产权体的建立和管理。OGC GML和CityGML[10]也提及并应用三维体的概念,却回避三维体从何而来以及如何维护。有关研究[2, 9, 11, 12, 13]和部分软件(如SketchUp、Oracle Spatial)可实现对简单三维体个体的有效性验证,而其存在的问题是:① 它是预先假设“三维体”已存在,然后去“事后”验证其有效性;② 其有效性验证严重依赖其假设的“三维体”的数据,并再次对其进行几何数据重构,是单向的,同时造成数据冗余,无法返回到数据库中;③ 只对简单孤立的单体而论,不支持非流形的奇异体,没有体与体之间的关系,无法识别复合体或者体集合。
相关文献详细描述了三维地籍的概念模型、三维房产语义模型和面向行政管理的地籍管理模型[14, 15, 16],本文着重于三维地籍中产权体的几何拓扑模型。对三维地籍来说,三维产权空间是主体对象,其定界和表达是管理的基础和关键。三维地籍要求管理的对象是三维产权体,它是具有一定语义的、封闭的真三维几何体,满足空间的几何和拓扑的一致性,并支持体积计算等基本的计算及分析。同时由于测量和管理的需要,原始的数据采集上都基于界址点、线和面,通过它们来构建三维产权体成为关键技术问题。本文认为用来表达地籍产权体的有效三维体满足:由面片构造和围成的;封闭的区域; 体内部是连通的。
现有技术表明,在二维空间,根据已有的线段可自动构造多边形及其拓扑关系[17],但在三维空间自动构造封闭体及其关系要复杂得多,文献[18]提出了基于面片的法向来搜索正/负侧体的基本思想,但没有具体讨论算法实施的过程。本文将基于提出的三维空间拓扑构造模型,论述初始构体的几何约束,详细描述自动构造三维空间的最小三维体的关键环节:面片排序和面片连接,提出自动构建最小三维体的基本思路,并就最小三维体的有效性、凸凹及带洞等奇异性进行讨论。 2 三维体自动构建
根据土地权属的要求,地籍产权体之间没有重复、交叠和渗透,空间的邻接和相离是产权体的基本关系[18, 19, 20] 。这一特征在2D空间中表现为宗地地块之间共享界址边/点;在3D空间中表现为产权体之间共享界址面/边/点。建立面/体、体/体的拓扑关系成为三维地籍建模的基础。本节先给出三维构体的拓扑模型,以及基本的原始数据约束,进而论述构体过程中两个重要环节:基于共享边的离散面片排序和最邻近面片的确定与连接,从而给出基于给定离散面片集合构造有效三维体的过程。 2.1 拓扑模型
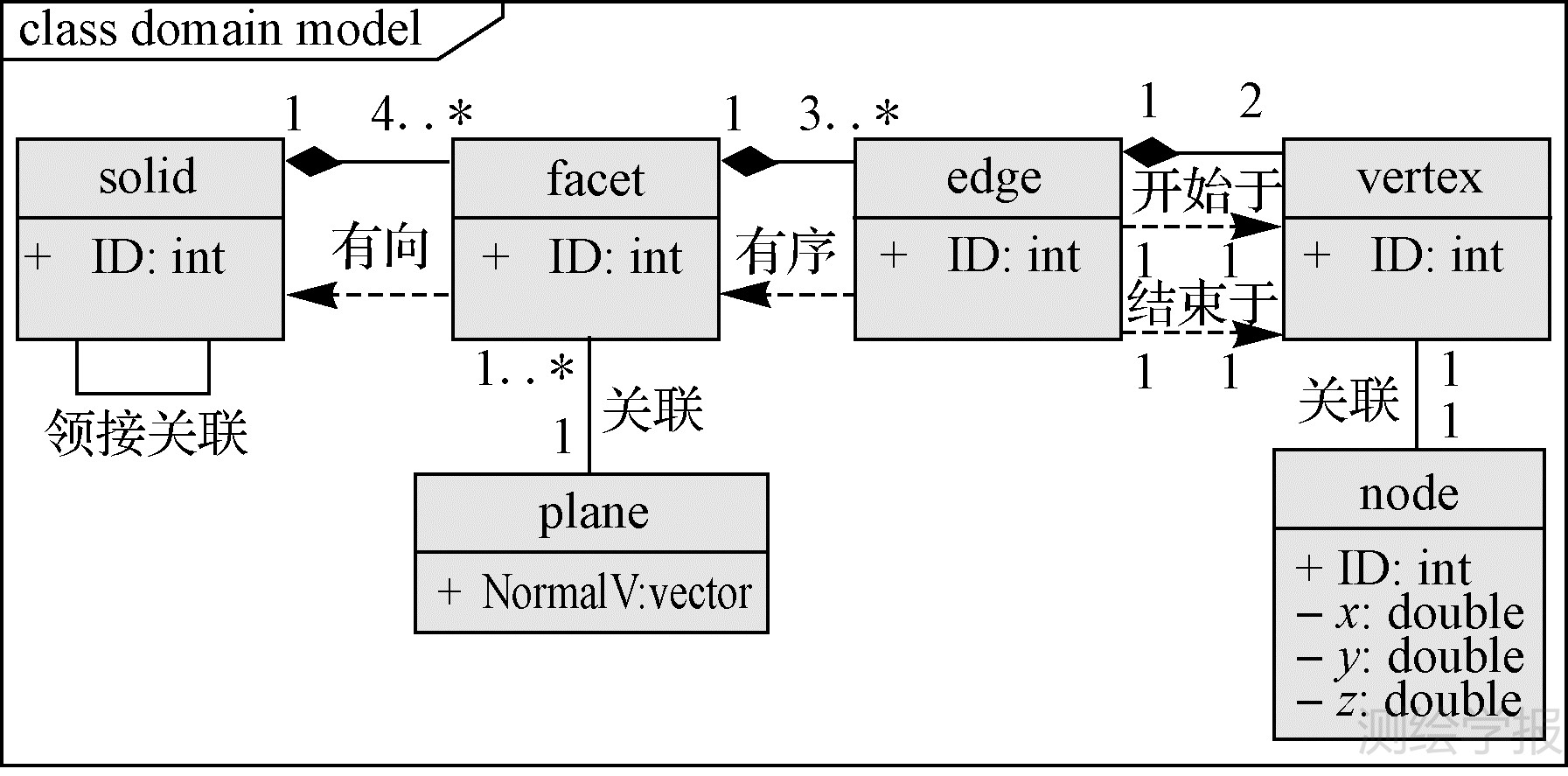
针对三维地籍要求产权体封闭的需求,采用图 1所示的三维空间拓扑模型。三维空间坐标仅存储在节点(node)上,其他采用ID关联指针。一个拓扑边(edge)由两个顶点(vertex)确定,可以根据初始数据采集的顺序指定为首末顶点,其实际的几何数据可以由内部形点来构成折线;一个面片(facet)是平面的,至少由3个拓扑边构成,并按照一定的顺序组织,其法向在构体时才能确定;一个三维封闭体(solid)由至少4个具有特定法向的面片封闭围成。这种n维几何元素由n-1维几何元素构造的原则,有效地避免了几何数据重复,同时保持了拓扑一致性。
|
| 图 1 三维体的拓扑关系构建模型 Fig. 1 3D topological model |
需要特别指出的是,面片是在三维空间中表达和描述的,其法方向在没有三维体的参照下,是不确定的,具有二向性,这也是三维空间中基于面片构建三维产权体的难点。只有当三维体确定时,才能确定构成体的面片的法向特征。这也是图 1中突出强调面片所处的平面(plane)、并围成三维体的原因,并且每个三维体对其构造面片都是有向的。 2.2 空间约束
三维空间中的离散面片作为基本的输入数据,要具有一致的空间分割,形成对三维空间的最大切割,或最详细切割,避免后期构造的体产生互斥。文献[2, 21]对构体约束条件讨论时指出多边形面片具有简单性和方向性,但其对面片方向性的确定已经先验地决定了体的存在。考虑到点、线、面数据是在地籍测绘中由测量师测定和处理,本文构体的空间几何约束如下:点数据咬合、无孤立点;边由多个顶点连续构成,互不相交重叠,无自相交;多边形面片为二维平面多边形(简称平多边形);三维曲面需分割成多个平多边形;多边形封闭,并允许具有内部环;多边形边界无自相交;多边形的内环不能与多边形边界相交;无孤立边和悬挂边;已构建基本的顶点、边和面片之间的拓扑关系 (不包括2D洞或环的信息,3D洞或环的信息是在构体后产生的)。
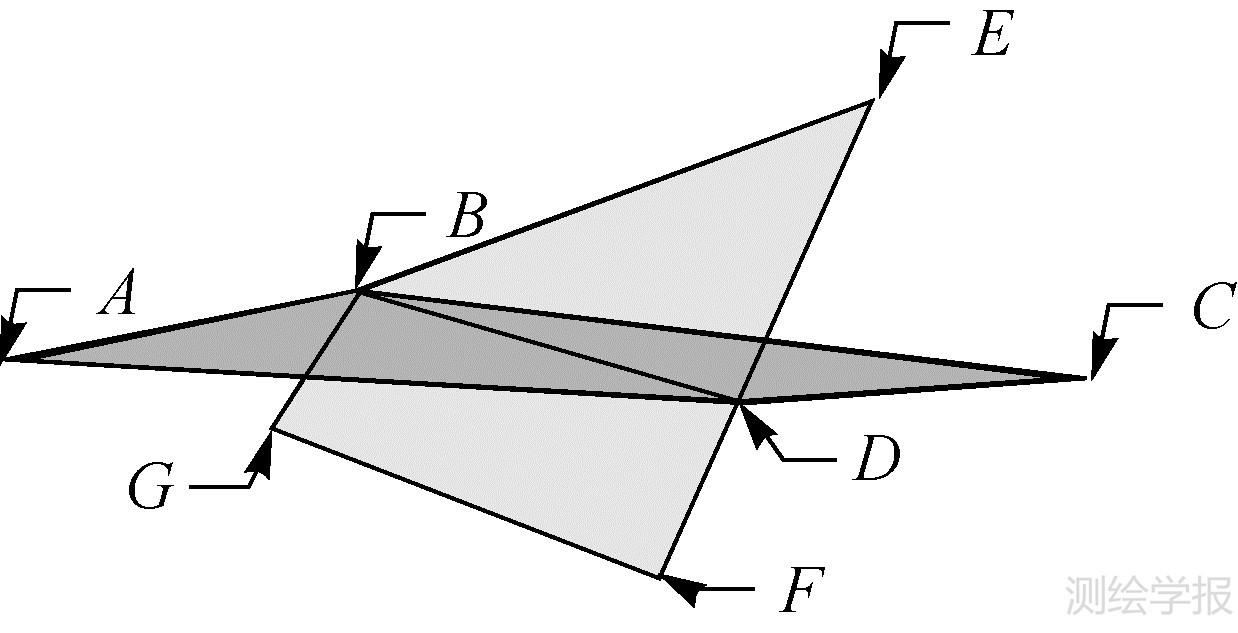
三维空间输入的面片经最大化分割后,三维空间中的多边形只共边、不相交,不存在多边形立体相交。如图 2,两个平多边形面片ABCD和BEFG相交于DB,此时的离散面片集合应为4个面片:ABD,BCD,BED和BDFG。三维空间中这种面片的最大分割,在支持奇异体和保障拓扑一致性的同时,还可以有效地避免体的穿越以及自我冲突的拓扑不一致。
|
| 图 2 三维中面片的最大分割图 Fig. 2 Maximal facet segmentation |
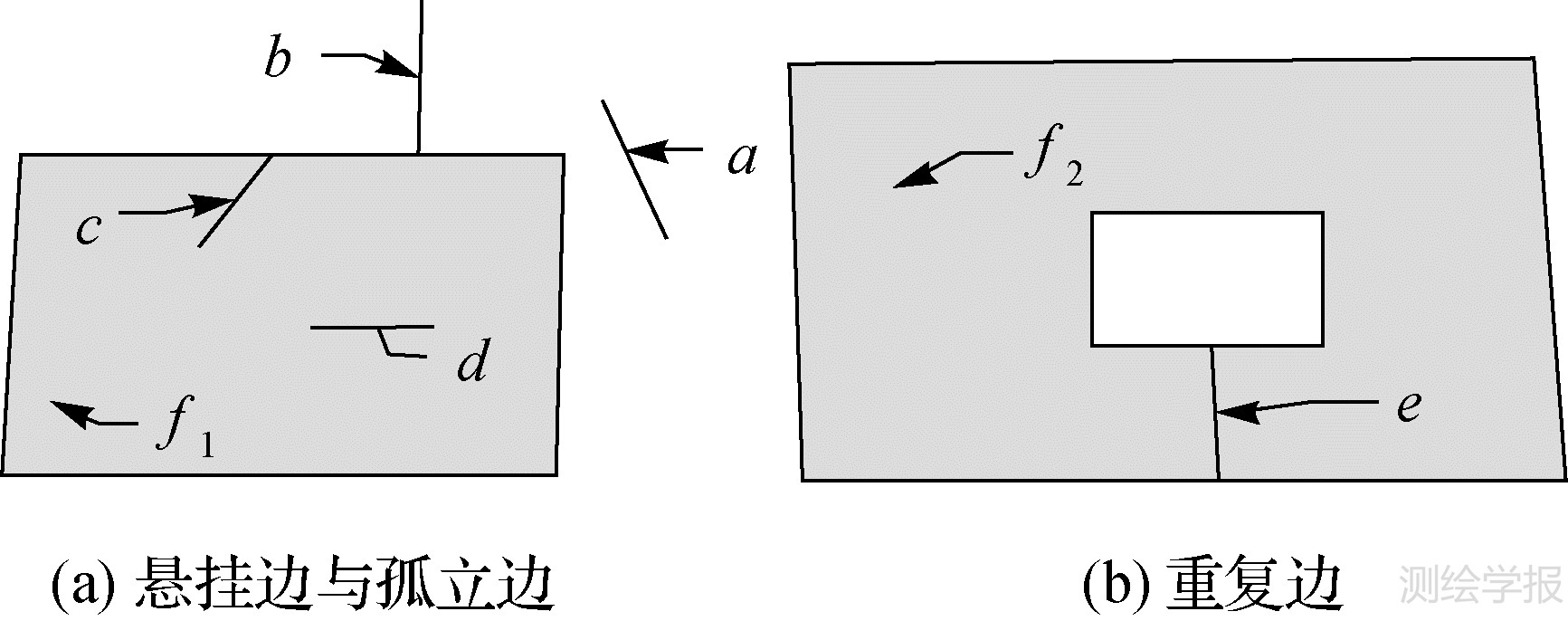
对最大分割后的面片进行拓扑构建,要求所有边都参与构建多边形。对图 3(a)的二维多边形来说,a和d分别为多边形外部和内部的孤立边、b和c为多边形外部和内部的悬挂边、图 3(b)中的边e为重复边,对本图多边形无意义,需删除;但是三维空间中它们可能是其他面片的最大化分割形成,允许参与其他多边形的构建(以支持3.2节中的奇异性)。
|
| 图 3 几何约束 Fig. 3 Geometric constraints |
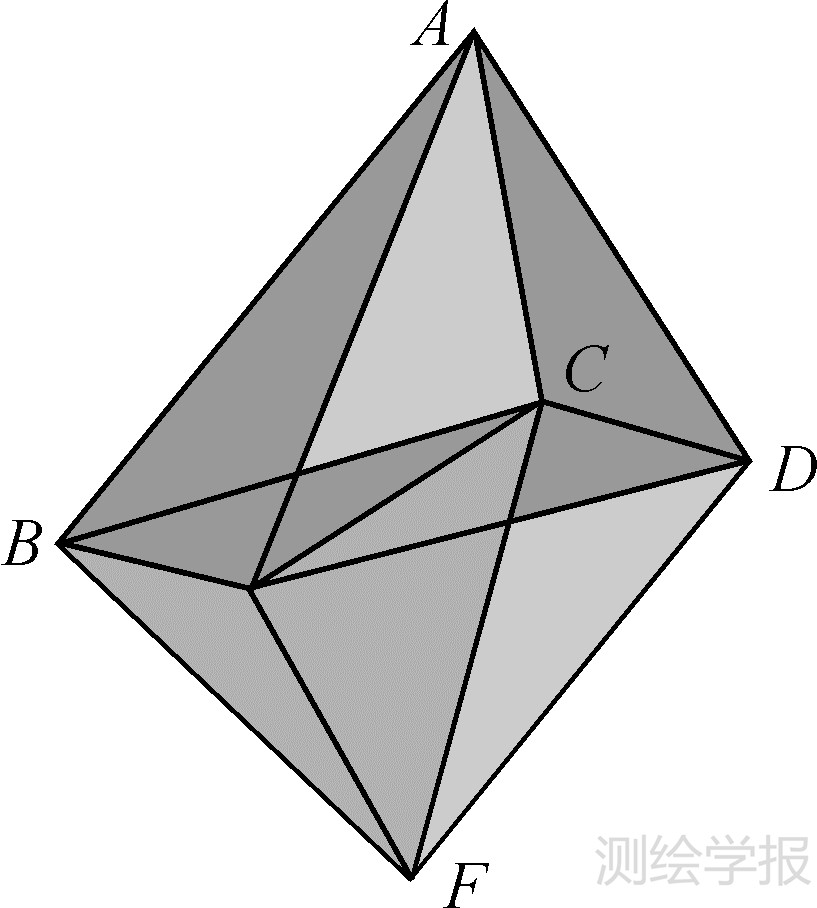
需要指出,在三维空间已知节点和边的关系不足以生成确定的体,若图 4下方已存在两个体BCEF和CDEF时,上部是存在两个体(ABCE和ACDE)还是只存在一个体(ABCDE)依赖于面ACE是否存在。面片的给定性是构体的前提,只有这种面的给定性才能保证三维构体的确定性和唯一性[18]且面片的给定性在地籍和房产测量中可以充分保证,这也是本文以面片为输入基本数据来构造三维体的原因。另外,本文中作为输入的已知面片本身不具有方向性;如果指定面片的方向时潜在确定三维体,那么和本文的出发点相悖。
|
| 图 4 三维中面片的给定性 Fig. 4 Certainty of the facets in 3D space |
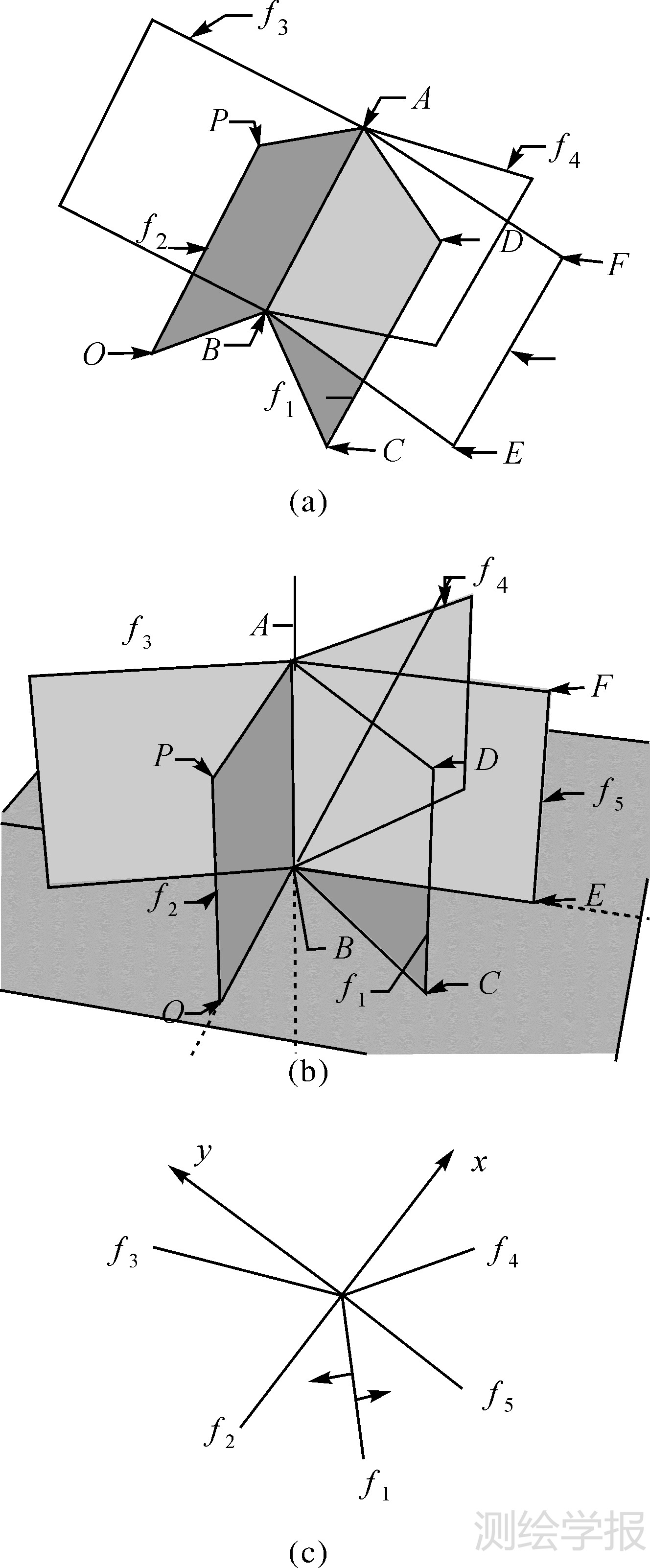
三维空间中面片之间的关系通过共享边来分析。称与某个边关联的面片个数为该边的度,显然,与度为1的边关联的面片是孤立面片或悬挂面片:若该面片的其他边的度都为1,则其是孤立面片;否则是悬挂面片。对度为2的边,说明其关联的两个面片在此边处产生“转折连接”;而对度大于2的边,说明必有至少两个潜在的三维体在该边处邻接。由于在三维空间中面片之间的位置关系难以明确地描述和界定,确定面片的相互关系和连接它们以形成三维体成为三维构体的关键,为此本文基于共享边的面片排序,把三维位置问题转化到二维空间,以确定它们的位置关系,作为本文构造三维体的基础。如图 5(a)所示,空间中共享边AB的面片束包含f1、f2、f3、f4、f5 5个面片,构造以AB为法向的垂面(图 5(b)),将面片集投影到该垂面上,可得到该平面内过一点的直线束(图 5(c));在该平面中,计算直线束中各直线之间的夹角,对该直线束中的各个直线进行顺/逆时针排序,进而得到共享边AB的面片集的序列;序列中两个相邻的面片之间必然是不包夹着其他面片,从而可以确定当前面片的邻近面片。设f1为当前面片,f5 和f2为其两个邻近面片,按照逆时针排序后,f5是下(后)一个最邻近面片,而f2为上(前)一个最邻近面片(图 5(c))。
|
| 图 5 基于共享边的面片集合的变换 Fig. 5 Spatial transformation of the facet sets sharing one common edge |
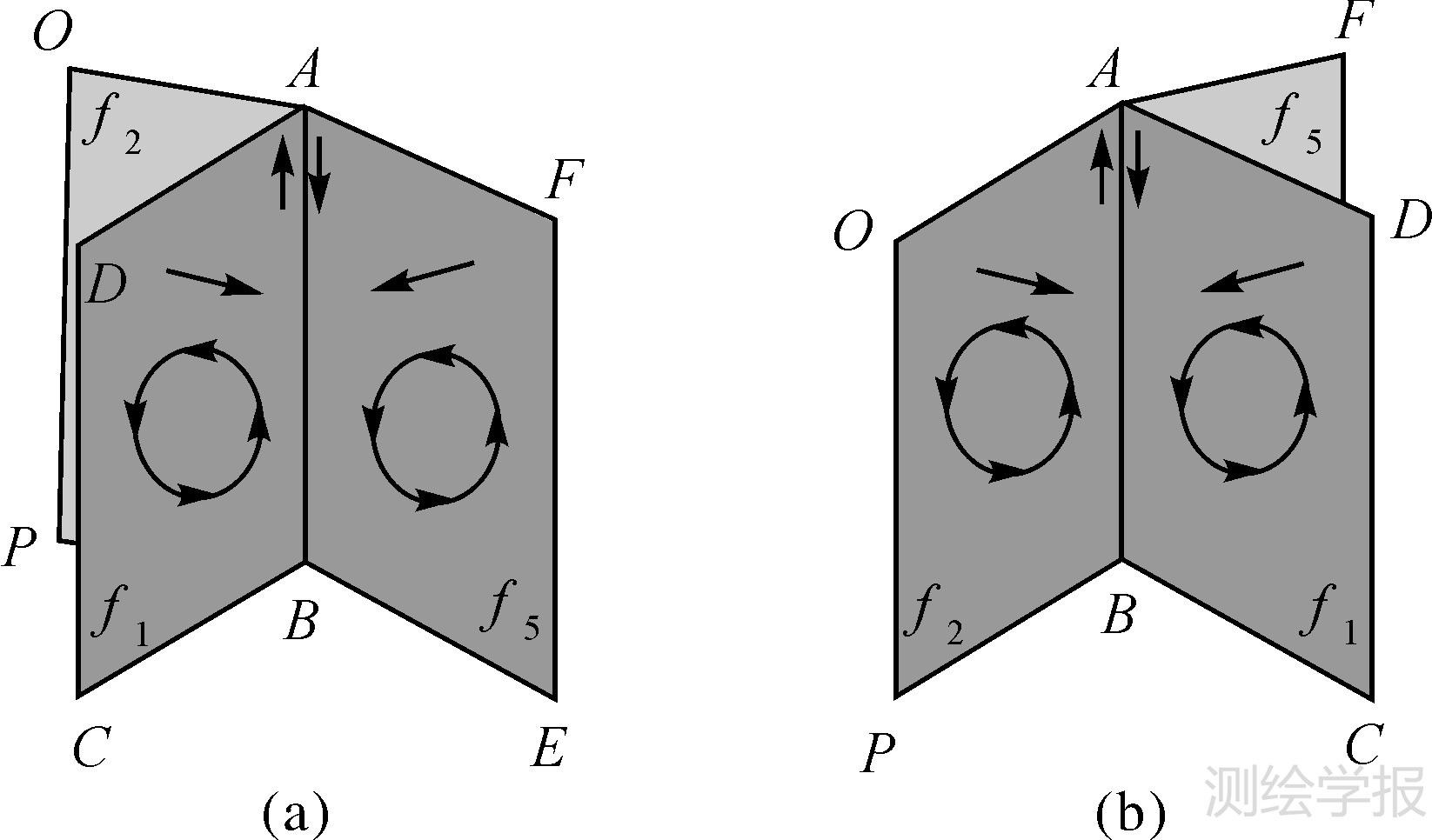
如前所述,三维空间中离散面片的法向不能预先统一的;只有在构体(或完成)时面片的法向才与三维体产生关系。这意味着2.3节中面片排序中确定的每个面的两个邻近面片都可能是构体时的候选后续面片,如果这样构体复杂度按照2的幂级增加。因此需在构体过程中通过某种逻辑判断从两个相邻面片中选择一个最邻近面片,以降低计算复杂度。由于构体时总会从某个面片的某一侧面(法向)出发,一方面决定了面片束排序时的方向及最邻近面片的确定,另一方面潜在确定了候选体的位置。如图 6(a)所示,指定当前面片f1的初始法向为向右,则其最邻近面片为f5;同时传递了潜在体的信息:面片f5的法向需朝向f1。而这种法向的传递可以通过多边形构造的边组织顺序来实现,如图 6(a)面片f1的法向指向右,其多边形边组织为BADCB,共享边AB的方向为从B到A,那么邻近面片f5的多边形边组织中AB的方向与其相反(从A到B)。因此得到f5的多边形组织顺序为ABEFA,所以其法向也指向f1(如图 6(a)所示)。类似的,从面片f1的法向反方向出发,f2为其最邻近面片,多边形的组织顺序如图 6(b)。
|
| 图 6 面片的法向传递和最邻近面片的确定 Fig. 6 The transitivity of the normal direction between two facets and the definition of the nearest neighbor facet |
该最邻近面片的确定和多边形组织的约束关系传递,逐步连接和缝合三维空间中面片,促成了三维体构建的可能性,并进一步保证三维构体的最小性。 2.5 最小三维体的自动构建
显然构体时在共享边处选择不同的面片来连接,构造的三维体是不同的。构建最小三维体,一是与真实的地籍产权体对应;二是能保证三维体的唯一存在性和构体结果唯一性,满足三维地籍建模中以产权体为管理单元的要求。最小三维体是由面片包围的一个单一且连续的三维封闭区域,并具有体积。最小体的复合、叠加或集群可形成复合体,这对群集三维产权体(如公寓)是十分重要的。在前述基于共享边的面片集合排序的条件下,面片根据“左右”邻近性选择最邻近的面片,逐步连接“缝合”成一个封闭体。最邻近面的传递使得最终构造的三维体是三维空间的最小体分割。
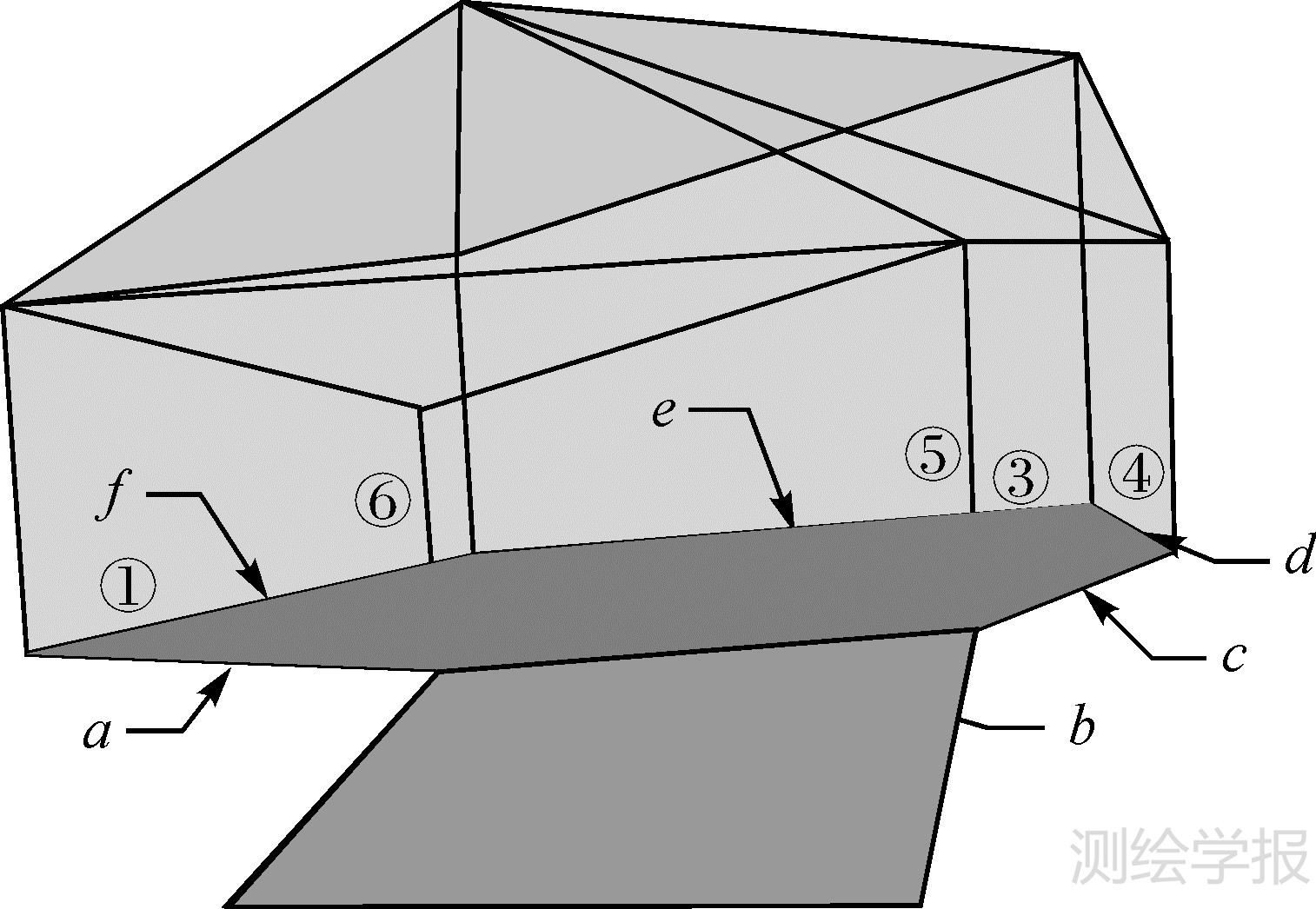
考虑到实际应用中二维宗地和三维产权体共存的情形,在构造三维体时需先标记和剔除出那些不参与构体的面片,因此需要对三维空间中的离散面片集合进行初始处理,包括:计算每个边的度;标记并剔除度为1的边关联的面片,用来排除孤立面片和悬挂面片(如图 7中面片FT);更新边的度,循环判断,直至没有度为1的面片;对边的度大于1的面片集合进行排序。
|
| 图 7 三维体搜索过程 Fig. 7 Workflow of solid construction |
然后,基于面片集合的三维最小体构建流程为:从任一面片和其任一侧面出发,通过面片的每一个边作为“桥梁”,基于此共享边的面片排序,确定面片左右最邻近的面片并连接记录,并以此传递下去,直到所有的面片都被访问,便能构造出三维空间所有的最小封闭体,及其存在的边/体和面/体的关联关系和体/体的邻接关系。由于面片二面性,具体实现时会遍历面片的两个侧面分别实施,保证全部潜在的三维体都被构建。图 7中指定初始面片OF和向上的法向,并创建一个数组来记录三维体的构成面片。通过初始面片OF的关联边(a、b、c、d、e、f)来搜索后续面片(①、②、③、④、⑤、⑥),并迭代搜索,直到体记录中没有新的面片加入,得到所构造的三维体的所有面片组,其有效性下节讨论。构建完成的每个三维体,再辅以产权等语义属性,以三维产权体目标入库。
在构体的过程中,已显性地获取了面片对三维体的拓扑构造:一是基于共享边的面片排序、最邻近面片确定以及构体过程,建立了三维体内部的线/面片、面片/体之间的拓扑关联关系;二是通过同一面片的二面性可以获得关联此面片的两个三维体,进而可建立共享面片的三维体之间的拓扑邻接关系,较为适宜三维地籍中群集三维体的建模。 3 讨论与实现 3.1 讨论
本方法充分满足了最小三维体的有效性验证。文献[9]指出在三维建模中要考虑三维实体的有效性确认问题,文献[13]结合Oracle分析了简单/复杂的面片和三维实体的有效性和无效性,但是其有效性的判断回避了一个关键问题:它们是假设“体”已存在,然后再按照类似2.2节的约束条件来判断其有效性。本文方法构建的三维体具有面片包围构造性和体的封闭性。首先,体的面片构造性是显而易见的。考虑到二维三维的并存,本文在构体前先识别出孤立和悬挂的面片,保证后续能够构造出三维体。算法终止的条件是所有的面片(及其所有的边)都参与了遍历,构建的三维体全部由面片围成,从拓扑角度确保了构建体的封闭性。通过共享边连接其最邻近面片,由于相邻面片不包夹其他任何片面[18] ,使得面片连接具有唯一性;而且这种连接具有传递性,从而使最后得到的三维体是最小的、唯一的和内连通的。
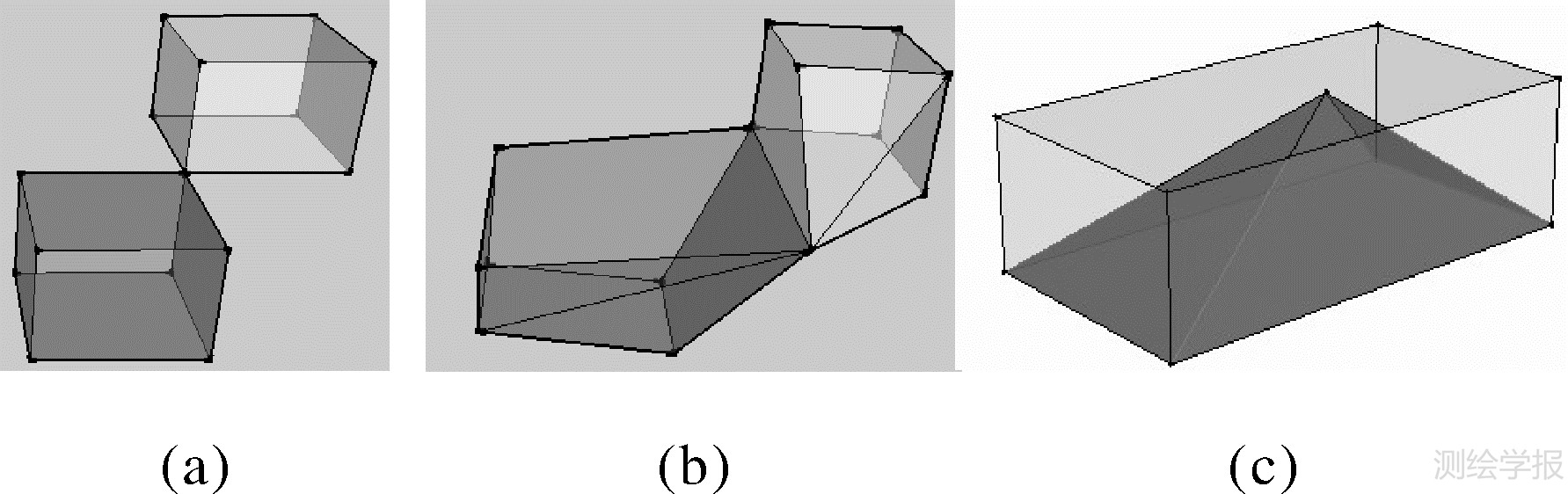
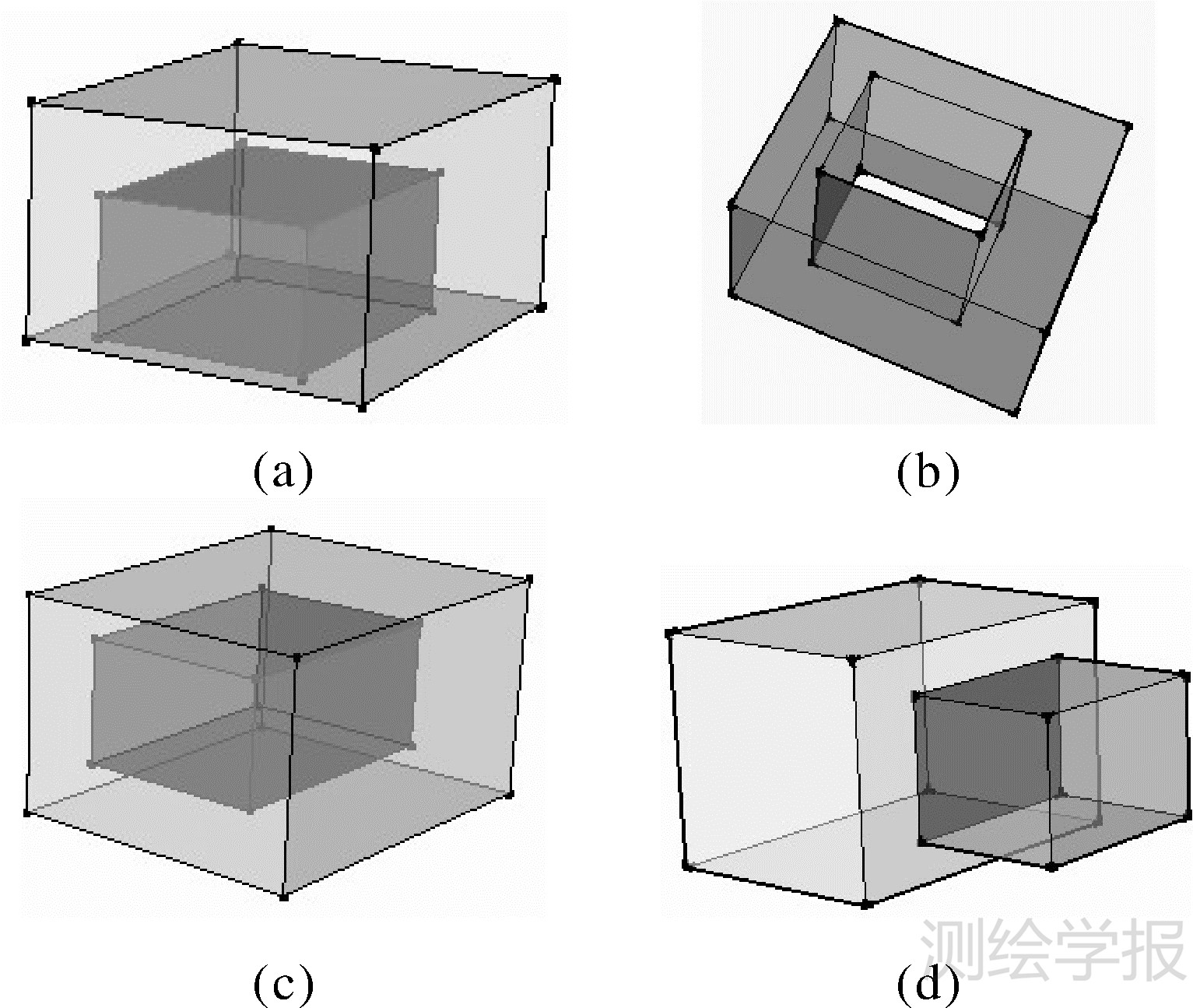
本方法严格遵循按维递增的拓扑构造原则,拓扑构造在相邻维度空间中进行,不是在跨维空间中进行,这使得跨维拓扑元素之间的关系不影响本算法的执行,如线不参与构造体。该过程一方面能有效地克服一些非流形的形体,构造后的三维体可具有各种奇异性,且支持三维体的凸凹性、包含性,可以用来建模表达三维地籍中客观存在的复杂产权体对象;另一方面能表达出产权体间的拓扑和位置关系。图 8中各体都属非流形,算法将它们构造为两个相互邻接或关联的三维体,且它们共享顶点、线或面,这是文献[9, 11, 13]“事后”验证方法所不能做到的。同时,基于面片的连接性的构体方法,一是实现了三维封闭多面体的内部无异常,不会出现低维的元素(线、面片);二是充分支持复杂带洞的多面体,二维洞的概念不适宜于三维中,其是否为“洞”是在三维体构建时才确定的,如图 9(a)和(d)中两个共享面中洞的不同,这也是2.2节中约束条件中未限制,因此算法准确建立具有面片连接的“空洞”的三维体如图 9(a)中底面带“洞”的外围体和图 9(b)的 “环”状体,对图 9(c)中的相互完全包含的两个体分别建立,但是它们之间的空间包含关系需要另外判断。
|
| 图 8 三维体的奇异性 Fig. 8 Singularity of the solids |
|
| 图 9 带“洞”的三维体 Fig. 9 Holes in 3D solids and 2D planes |
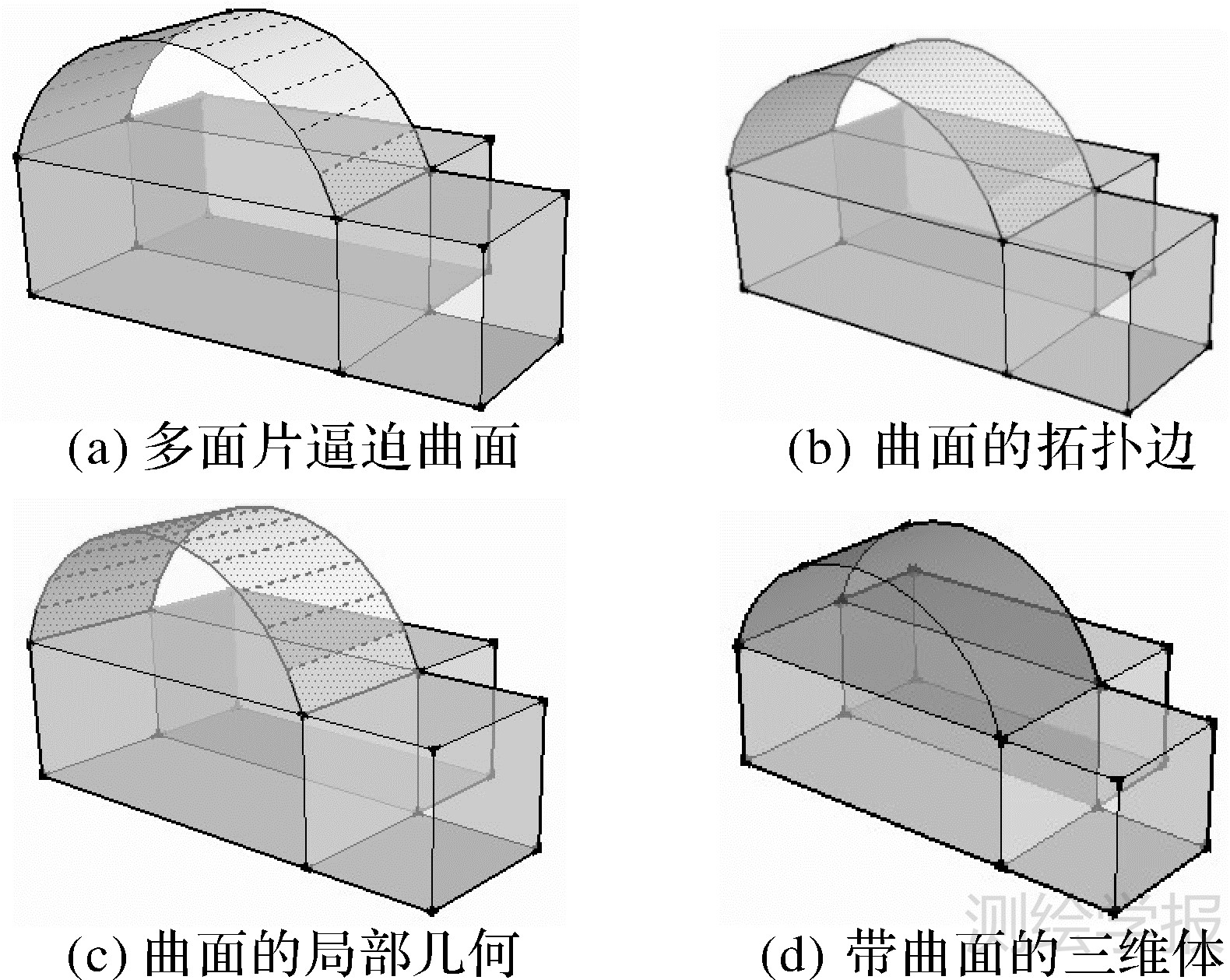
本方法是基于共享边的面片连接,“面片”和拓扑“度”的概念可以进一步扩展,面片可以是多样的:一是可通过连续的平多边形面片来逼近曲面,此时每个面片都参与拓构建扑(图 10(a)的曲面);二是拓扑面片可扩展为整个曲面面片(图 10(b)),其具有自身的几何多边形(可以为曲面)(图 10(c)),但是在实施面片排序时,只需以其拓扑边所在的局部几何多边形(图 10(a)中的矩形)来代表整个拓扑面片,参与计算实施最小体构建(图 10(d)),从而实现面片数据在组织上的拓扑和几何一致性。
|
| 图 10 面片的扩展 Fig. 10 Scalability of the curve facet with consistent geometry and topology |
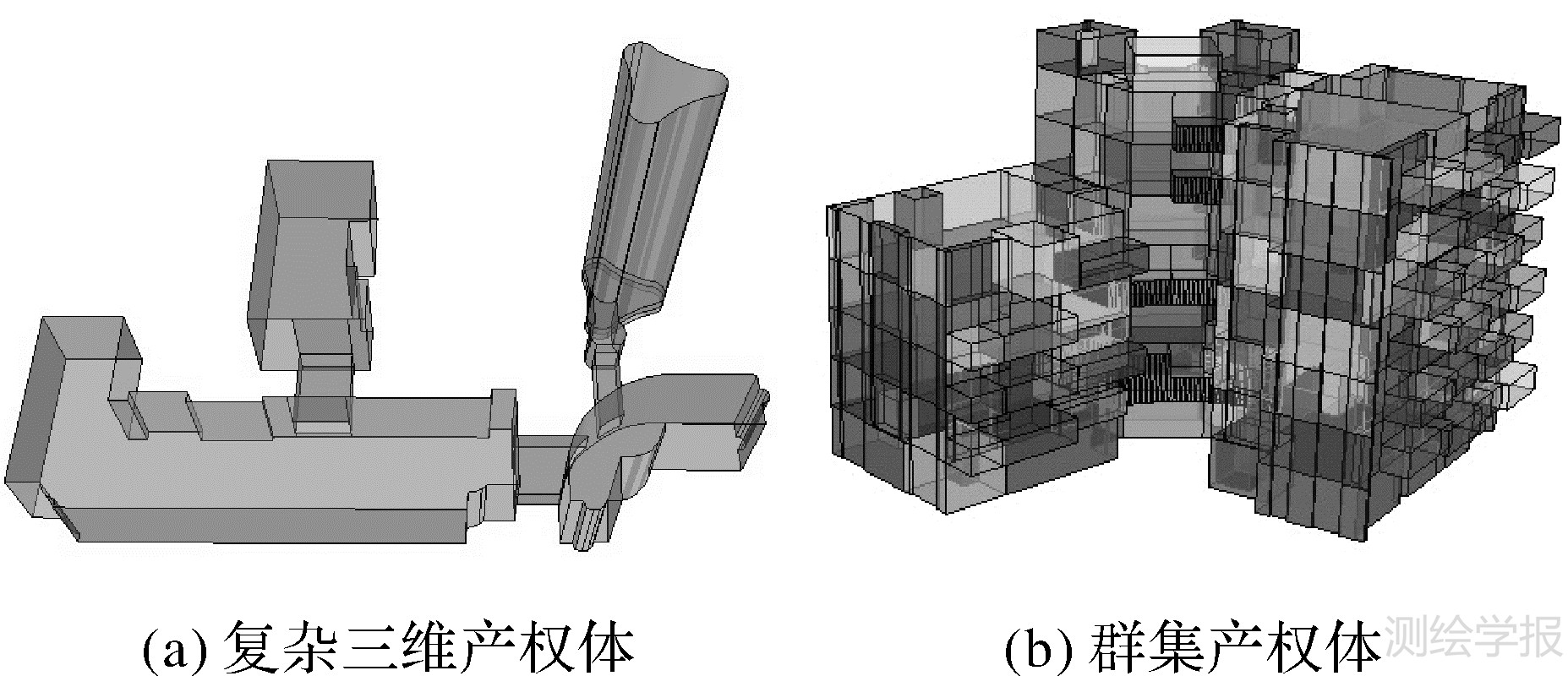
三维空间中的离散面片数据可以通过各种三维软件(如SketchUp,AutoCAD)来制作,针对三维地籍来说,三维面片数据是由测量师通过测量绘图来实现的指定面片,具有确定地分割性和给定性。基于文中自动构体方法,在Google SketchUp平台上,利用Ruby 开发语言,笔者实现了基于离散面片集合的三维产权体模型的自动构建和拓扑维护,完成三维地籍的建模和入库。图 11(a)展现了一个由4栋联体建筑和3个过街通道构成的建筑群的建筑空间,输入数据为892个面片数据,利用文中算法构造成一个封闭体;图 11(b)则以真实的三维房产数据为例,共有6584个面片,基于本文方法逐一识别,并构建其中的每个体产权体(共246个),最终形成邻接的群集三维产权体。
|
| 图 11 复杂和群集三维产权体案例 Fig. 11 Cases of the construction of the 3D cadastral object and its assembly |
本文从三维地籍的需求出发,在测量师能充分提供界址点、线、面的情况下,提出了一种正面直接构建三维几何封闭体的方法,利用三维空间中的离散面片集合,在未知任何三维体信息及不修改数据的情况下,通过面片的排序和连接来构造唯一的最小三维体,并建立三维体的面/体、体/体之间的拓扑关系;同时支持凸凹、带洞等奇异体,从而支持三维产权体的自动构建和表达。本文限于构造最小体,它是三维地籍管理的最小单位,最小体的不同组合结果各不相同,具有很强的不确定性;三维体的群集集合在拓扑构建和产权体群集(图 11(b))管理上具有明确的意义。最大三维体是文中方法构建结果的一个特例:对孤立的三维体来说,最大体和最小体几何边界上重合,方向相反;对最小体群集来说,最大体几何上是它们的最小外包(方向相反)。另外本文重点在最小体的构建方法和原理上进行探讨,有关具体实现的数据结构以及数据重组和维护等问题,有待进一步研究。
致 谢:感谢赵志刚、虞昌斌在有关细节问题上的探讨和建议。
| [1] | GUO Wei, CHEN Jun. The Formal Description of Topological Spatial Relationship in 3D Based on Point Set Topology[J]. Acta Geodaetica et Cartographica Sinica, 1997, 26(2):122-127.(郭薇, 陈军.基于点集拓扑学的三维拓扑空间关系形式化描述[J].测绘学报, 1997, 26(2):122-127. ) |
| [2] | KHUAN C, ABDUL RAHMAN A, ZLATANOVA S. 3D Solids and Their Management in DBMS[C]//Proceedings of Advances in 3D Geoinformation Systems.Heidelberg: Springer, 2008:279-313. |
| [3] | YANG Bisheng, JIANG Shaobo. Generating Levels of Detail of 3D Building Models Based on Cutting Loops Decomposition[J]. Acta Geodaetica et Cartographica Sinica, 2011, 40(5):575-581.(杨必胜, 姜少波.基于切割环分解的三维建筑物细节层次模型构造[J].测绘学报, 2011, 40(5):575-581. ) |
| [4] | SUN Xuan, YANG Bisheng, LI Qingquan. Structural Segmentation Method for 3D Building Models Based on Voxel Analysis[J]. Acta Geodaetica et Cartographica Sinica, 2011, 40(5):532-537.(孙轩, 杨必胜, 李清泉.基于体元分析的三维建筑物模型结构化分割方法[J].测绘学报, 2011, 40(5):532-537.) |
| [5] | LEDOUX H, MEIJERS M. Extruding Building Footprints to Create Topologically Consistent 3D City Models[C] Boca Rotan: CRC Press, 2009:39-48. | //Proceedings of Urban and Regional Data Management (UDMS 2009).
| [6] | LEDOUX H, MEIJERS M. Topologically Consistent 3D City Models Obtained by Extrusion[J]. International Journal of Geographical Information Science, 2011, 25(4): 557-574. |
| [7] | YING Shen, LI Lin, GUO Renzhong. Building 3D Cadastral System Based on 2D Surveying Plans with SketchUp[J]. Geo-Spatial Information Science, 2011, 14(2):129-136. |
| [8] | HORNA S, MENEVEAUX D, DAMIAND G, et al. Consistency Constraints and 3D Building Reconstruction[J]. Computer-Aided Design, 2009, 41(1): 13-27. |
| [9] | ARENS C, STOTER J, VAN OOSTEROM P. Modelling 3D Spatial Objects in a Geo-DBMS Using a 3D Primitive[J]. Computers & Geosciences, 2005, 31(2):165-177. |
| [10] | City Geography Markup Language (CityGML) Encoding Standard[EB/OL]. [2011-5-8]. . |
| [11] | VAN OOSTEROM P, QUAK W, TIJSSEN T. About Invalid, Valid and Clean Polygons[C]//Proceedings of Developments in Spatial Data Handling. New York: Springer-Verlag, 2004. 1-16. |
| [12] | THOMPSON R, VAN OOSTEROM P. Modelling and Validation of 3D Cadastral Object[C] //Proceedings of Urban and Regional Data Management:UDMS Annual.London: Taylor & Francis Group, 2011: 7-23. |
| [13] | KAZAR BM, KOTHURI R, VAN OOSTEROM P, et al. On Valid and Invalid Three-Dimensional Geometries[C]//Proceedings of Advances in 3D Geoinformation Systems. Heidelberg: Springer, 2008:19-46. |
| [14] | LIN Henggui, GUO Renzhong. Design of 3D Cadastrae Conceptual Model[J]. Geomatics and Information Science of Wuhan University, 2006, 31(7):643-645. (林亨贵, 郭仁忠.三维地籍概念模型的设计研究[J].武汉大学学报:信息科学版, 2006, 31(7):643-645.) |
| [15] | ZHU qing, HU Mingyuan, Semantics-based LOD Models of 3D House Property[J], Acta Geodaetica et Cartographica Sinica, 2008, 37(4):514-520. (朱庆, 胡明远.基于语义的多细节层次3维房产模型[J].测绘学报, 2008, 37(4):514-520.) |
| [16] | ISO/DIS 19152 (2012) ISO/TC 211 Geographic Information - Land Administration Domain Model (LADM)[EB/OL].[2011-5-8] . |
| [17] | YAN Haowen, YANG Weifang, CHEN Quangong, et al. A Fast Algorithm of Topological Polygon Auto-Construction Based on Azimuth Calculation[J]. Journal of Image and Graphics, 2000, 5A(7):563-567. (闫浩文, 杨维芳, 陈全功, 等.基于方位角计算的拓扑多边形自动构建快速算法[J].中国图象图形学报, 2000, 5A(7):563-567.) |
| [18] | GUO Renzhong, YING Shen. Three Dimensional Cadaster Analysis and Data Delivery[J]. China Land Science, 2010, 24 (12): 45-51. (郭仁忠, 应申.三维地籍形态分析与数据表达[J].中国土地科学, 2010, 24 (12): 45-51.) |
| [19] | STOTER J E. 3D Cadastre[D]. Delft: Delft University of Technology, 2004. |
| [20] | STOTER J E, VAN OOSTEROM P. Technological Aspects of a Full 3D Cadastral Registration[J]. International Journal of Geographical Information Science, 2005, 19(6): 669-696. |
| [21] | CHANDRA N, GOVARDHAN A. Design and Implementation of Polyhedron as a Primitive to Represent 3D Spatial Objects[J]. Journal of Theoretical and Applied Information Technology, 2008, 4(3):212-218. |



