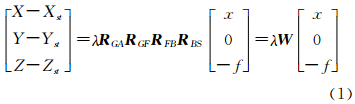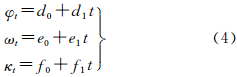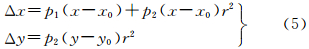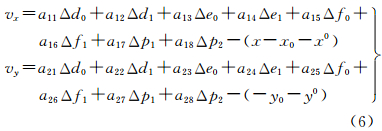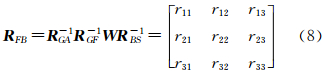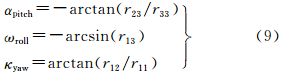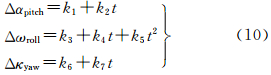自1999年美国首颗高分辨率遥感卫星IKONOS发射升空以后,国际商用遥感卫星不断出现,IKONOS以其最高0.82 m的空间分辨率影像满足了很多行业的应用需求。2001年美国又发射了QuickBird遥感卫星,更是将影像空间分辨率提高到了0.61 m。其他的如SPOT-5、EROS A1以及CBERS-02B等卫星遥感影像的空间分辨率都达到了米级[1]。
虽然国产卫星遥感影像的空间分辨率在不断提高,但与国外同等分辨率的卫星遥感影像相比,几何处理精度要低1~2个数量级,难以满足国民经济建设的应用需求,严重降低了卫星遥感影像的使用效率。研究表明,高分辨率卫星遥感影像的姿态角误差是制约其对地目标定位精度的主要因素[2]。文献[3]提出可以通过一个广义的偏置矩阵来校正这些误差所引起的成像偏差;文献[4]详细分析了偏置角对目标定位精度的影响,分别求解偏置角,改进了求解偏置矩阵的方法;类似的,文献[5]对CBERS-02B影像进行了几何检校,利用多景影像求解出一个总体的偏置矩阵进而完成了影像的几何校正。由于偏置矩阵本身并没有严格的物理意义,因此不能确切地表达影像姿态角的系统误差。文献[6]根据CCD的拼接和排列误差提出了相应的系统误差检校模型,将IRS-1C卫星遥感影像的直接对地目标定位精度从±50 GSD提高到了±2 GSD的水平,但此模型因未顾及姿态角的系统误差而不能直接用于国产高分辨率卫星遥感影像。文献[7]对机载三线阵传感器ADS40进行了几何检校,提出了比较稳健的检校方案,但其模型无法直接用于高分辨率卫星遥感影像的几何检校。文献[8]提出了影像姿态角常差检校模型,利用单个地面控制点检校出的常差值对卫星遥感影像的角元素进行系统误差补偿后,能够将影像对地目标定位的精度提高到±4像素的水平。本文从卫星遥感影像严格几何处理模型出发,研究影像姿态角系统误差检校模型和方法,通过对法国SPOT-5卫星和国产CBERS-02B卫星遥感影像的试验,并与影像姿态角常差检校方法[8]进行对比,以验证本文所提出的姿态角系统误差检校方法的有效性和优越性。
1 卫星遥感影像姿态角系统误差检校原理由于卫星遥感平台携带的星像仪、陀螺仪等测姿系统测定的传感器姿态角通常含有系统误差,国产遥感卫星尤其如此,在影像几何处理之前应予以改正[9]。尽管当今的定轨技术所测定的传感器位置参数也带有一定的误差,但其精度相对于姿态角要高得多,对影像直接对地目标定位结果的影响几乎可以忽略不计[8, 9]。因此,传感器姿态角误差是影响目标定位精度的主要因素。本文的影像姿态角系统误差检校方法是在不考虑传感器位置误差的前提下,对扩展共线条件方程中角元素随成像时刻线性变化、并辅之合适的像平面坐标系统误差改正而进行影像定向,将所获得的“精确”影像姿态角与传感器姿态测量数据进行比较,以求得传感器姿态角的系统误差补偿参数,从而实现对影像姿态角的系统误差检校。
1.1 卫星遥感影像严格几何处理模型一般的,高分辨率光学卫星遥感影像为线阵推扫式成像,在t时刻获取的任一像点坐标(x,0)与其对应的物方空间坐标(X,Y,Z)存在如下严格关系[10, 11]
式中,λ为尺度因子;f为传感器主距;(Xst,Yst,Zst)为地面点成像时刻卫星在地心直角坐标系下的三维空间坐标
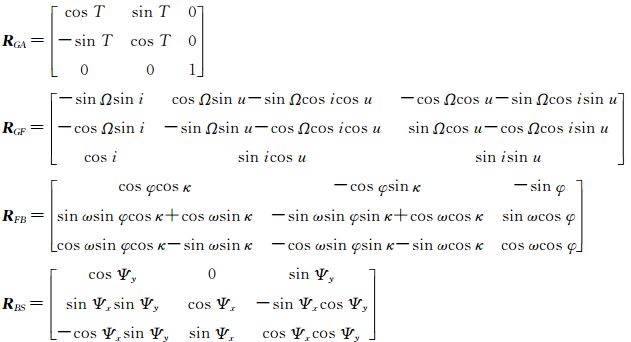
这里,T=99.089 927 4+0.985 612 286d+360.895 612T/86 400为春分点的格林尼治恒星时,d为从1950-1-1零时到成像时刻之间的整数日,T为当前时刻;Ψx、Ψy为传感器在扫描线方向和卫星运行方向的侧视角;i为卫星轨道倾角;Ω为卫星轨道面的升交点赤径;u=ωp+c,其中ωP为卫星轨道近地点角距,c为轨道真近点角;φ、ω、k为扫描行影像的航向倾角(pitch)、旁向倾角(roll)和像片旋角(yaw)[12, 13]。
1.2 影像姿态角严格计算模型由式(1)可以导出附加系统误差改正项的推扫式成像扩展共线条件方程
式中,(x0,y0)为像主点坐标;a1~c3为t时刻对应扫描行影像坐标系与物方空间坐标系间的旋转角(φt,ωt,κt)所构成的正交变换矩阵W中的9个方向余弦,具体数值为
一般说来,卫星遥感平台运行比较平稳,实际处理中通常是将每一扫描行的6个外方位元素表示为成像时刻t的多项式函数,这里将3个外方位角元素表示成t的线性函数[14]
式中,d0、d1、e0、e1、f0、f1为线性变换系数。
且将式(2)中的像点坐标系统误差改正项(Δx,Δy)表示为
式中,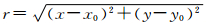 为像点的向径;p1主要用于改正由于传感器主距的变化而产生的误差[6];p2为改正传感器物镜径向畸变差的参数[15, 16]。
为像点的向径;p1主要用于改正由于传感器主距的变化而产生的误差[6];p2为改正传感器物镜径向畸变差的参数[15, 16]。
将像点坐标当做观测值、式(4)和式(5)中的系数视为未知数,对式(2)线性化得误差方程的一般形式为
式中,(vx,vy)为像点坐标观测值的残差;(x0,y0)为用未知数近似值代入式(2)求得的像点坐标值;a11~a28为相应的偏导数值[17, 18]
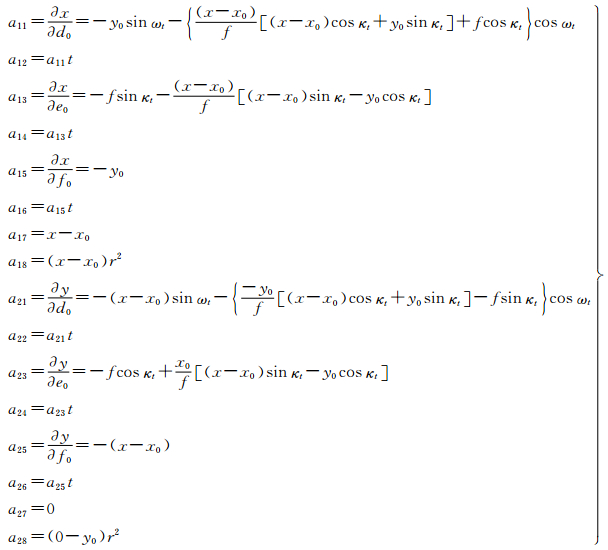
式(6)的矩阵形式为
式中
V=[vxvy]T
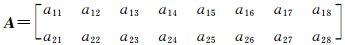
x=[Δd0 Δd1 Δe0 Δe1 Δf0 Δf1 Δp1 Δp2]T
l=[x-x0-x0-y0-y0]T
若在影像上量测了n个像点,假设像点坐标观测值等精度不相关,则根据最小二乘平差原理就可解得所有未知数的最或是值,将其代入式(4)便可得到影像的“精确”外方位角元素φt、ωt和κt,由式(3)可计算出旋转矩阵W,由式(1)便可反算出卫星本体坐标系到卫星轨道坐标系的正交变换矩阵RFB,即
进而可以得到传感器姿态角pitch、roll和yaw
1.4 影像姿态角系统误差检校模型研究表明,影像姿态角常差检校是补偿影像姿态角误差的一种行之有效的方法[8]。但其所求解的3个角度常差值实质上是式(4)中的d0、e0和f0,即高分辨率卫星遥感影像的广义外方位角元素值,正是这3个外方位角元素的余弦值构成了式(1)中的矩阵W。事实上,矩阵W是由一系列坐标正交变换矩阵相乘所得到的,不但包含了传感器姿态角pitch、roll和yaw所构成的旋转矩阵RFB,而且也包含了由卫星轨道参数所决定的旋转矩阵RGA和RGF。由于这两个正交变换矩阵实际上反映的是影像外方位线元素及传感器的速度矢量[5],考虑到通常情况下卫星测轨精度远优于定姿精度的实际,如果只是按照姿态角常差检校理论来改正上述3个广义上的影像外方位角元素误差,事实上也将影像外方位线元素的误差一并改正了。换言之,影像姿态角常差检校并不能直接反映卫星遥感影像的姿态角误差的变化规律,只有通过式(9)计算出影像姿态角的精确值才能直观表达高分辨率卫星遥感影像姿态角误差的真正变化规律,这正是本文提出影像姿态角系统误差检校模型的理论依据。
文献[19]指出,在卫星运行不太长的一段时期内,传感器姿态角中的pitch和yaw的误差几乎是随着影像行坐标而呈线性变化的。对于线阵推扫式卫星遥感影像而言,行坐标是扫描时刻t的函数,因此这两个角的误差可以用成像时刻t的一次函数来模拟。此外,文献[20]指出,高分辨率遥感卫星中HR相机的TDI CCD行积分时间调整具有同步性。卫星平台大约每隔十几秒对行积分时间会产生约0.000 667 ms的跳变,在行积分时间跳变的一个周期内,片间垂直偏移量将产生一个整体的变化,且存在一个线性过渡阶段[21]。这部分误差反映到传感器姿态角上就是roll的误差。
综合考虑上述各种因素,在一定的成像时间段内,卫星遥感影像姿态角的系统误差可以用成像时刻t的函数来模拟,从而得到本文的姿态角系统误差补偿模型
2 试验及其结果分析 2.1 试验设计本文选用SPOT-5和CBERS-02B卫星各两景一级影像(仅实施基本的辐射和简单的几何改正)进行试验。其中,两景SPOT-5影像于2004年10月拍摄于河北迁西地区,时间相隔3天,地面分辨率为5 m,采用超分辨率技术处理后可达到2.5 m,像幅大小为12 000×12 000 像素,覆盖区域的最大高差约为20 m;两景CBERS-02B影像分别于2008年1月拍摄于河北迁西地区和12月拍摄于河南嵩山地区,地面分辨率为2.6 m,像幅大小为4096×15 000像素。在SPOT-5影像上采用人工判读方法量测了75个均匀分布的地面控制点,在CBERS-02B影像上采用同样方法量测了50个均匀分布的地面控制点。迁西地区的地面控制点坐标为利用该区域1∶60 000航摄影像经WuCAPS系统采用GPS辅助光束法区域网平差方法[22]加密得到,平面位置精度为±2.5 m,高程精度为±2.0 m;嵩山地区地面控制点坐标利用该区域0.5 m GSD的ADS40影像通过ORIMA软件进行空中三角测量获到[23],其平面位置和高程精度均优于±0.45 m,完全可以满足作为卫星影像控制点和检查点的需要。所有地面控制点均为明显地物点,如道路交叉口、房屋拐角点等,通过人工比对卫星遥感影像间以及卫星遥感影像与航摄影像之间的同名特征点而获得。
2.2 直接对地目标定位误差分析首先根据式(1)分别对SPOT-5和CBERS-02B影像进行直接对地目标定位,由地面检查点计算得到的地面坐标残差列于表 1和表 2。
| m | ||||||||
| 影像 | 检查点数 | 最大残差 | 最小残差 | 中误差 | ||||
| X | Y | X | Y | X | Y | 平面 | ||
| 左 | 75 | 1.17 | 7.01 | 33.44 | 38.59 | 15.29 | 18.12 | 23.71 |
| 右 | 75 | 0.13 | 2.24 | 19.93 | 23.22 | 6.12 | 11.98 | 13.45 |
| m | ||||||||
| 影像 | 检查点数 | 最大残差 | 最小残差 | 中误差 | ||||
| X | Y | X | Y | X | Y | 平面 | ||
| 迁西 | 50 | 1 000.12 | 4 923.17 | 11 411.57 | 8 553.01 | 7 205.40 | 6 670.00 | 9 818.69 |
| 嵩山 | 50 | 130.54 | 1 466.13 | 9 858.09 | 6 223.35 | 3 156.94 | 5 662.43 | 6 483.00 |
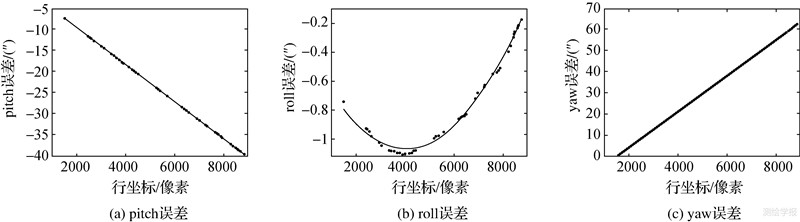
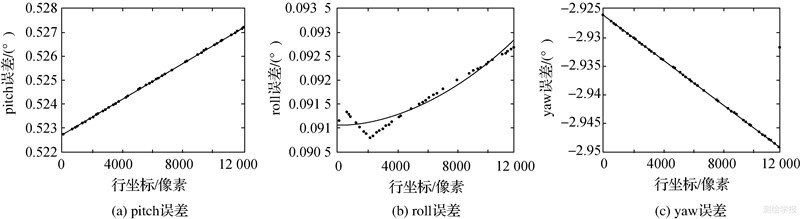
比较表 1和表 2发现,SPOT-5影像的直接对地目标定位精度远远高于CBERS-02B影像的对地目标定位精度。这是因为二者定轨精度存在一定的差距:SPOT-5的DORIS定轨精度可以达到分米级,而CBERS-02B的定轨精度仅为±30 m[9];而且影像直接对地目标定位精度受姿态测量误差影响最大。图 1和图 2示意了由式(9)计算出的影像姿态角值与其测量值的差值随影像行坐标的变化情况(图上的·点),经采用最小二乘拟合法对各离散点进行线性拟合可以获得3个角度差值的变化趋势(图中的实线)。
|
| 图 1 SPOT-5影像姿态角误差随影像行坐标的变化趋势图 Fig. 1 Change tendency of SPOT-5 image attitude errors with line coordinates |
|
| 图 2 CBERS-02B影像姿态角误差随影像行坐标的变化趋势图 Fig. 2 Change tendency of CBERS-02B image attitude errors with line coordinates |
从图 1和图 2可以看出,pitch和yaw的误差随着影像行坐标而线性变化,而roll的误差则随着影像行坐标呈抛物线变化,这说明本文中的姿态角系统误差模型是合适的。
比较图 1(b)与图 2(b)可知,相对于CBERS-02B影像,SPOT-5影像的行积分跳变要平缓得多。当用t的二次函数来拟合此项误差时,SPOT-5影像比CBERS-02B影像可获得更好的效果。
2.3 影像姿态角误差补偿后的直接对地目标定位误差分析对SPOT-5和CBERS-02B影像分别在影像4个角点和中心区域各布设一个平高地面控制点,利用本文中的影像姿态角系统误差模型进行检校,最终可求得式(10)中的7个参数,依据这7个参数补偿影像姿态角误差后的直接对地目标定位结果列于表 3和表 4,表中同时给出了利用影像姿态角常差检校模型补偿后的直接对地目标定位结果。
| m | |||||||||
| 影像 | 检校方法 | 检查点数 | 最大残差 | 最小残差 | 中误差 | ||||
| X | Y | X | Y | X | Y | 平面 | |||
| 左 | 本文方法 | 70 | 0.04 | 0.02 | 18.43 | 23.12 | 5.90 | 4.27 | 7.28 |
| 左 | 常差检校法 | 70 | 0.07 | 0.02 | 27.42 | 23.01 | 10.05 | 4.42 | 10.98 |
| 右 | 本文方法 | 70 | 0.09 | 0.01 | 16.25 | 11.12 | 5.55 | 3.10 | 6.36 |
| 右 | 常差检校法 | 70 | 0.12 | 0.01 | 17.21 | 12.09 | 5.60 | 3.16 | 6.43 |
| m | |||||||||
| 影像 | 检校方法 | 检查点数 | 最大残差 | 最小残差 | 中误差 | ||||
| X | Y | X | Y | X | Y | 平面 | |||
| 迁西 | 本文方法 | 45 | 0.01 | 0.00 | 9.66 | 5.36 | 3.92 | 1.64 | 4.25 |
| 迁西 | 常差检校法 | 45 | 0.01 | 0.01 | 12.17 | 16.55 | 4.76 | 4.74 | 6.72 |
| 嵩山 | 本文方法 | 45 | 0.19 | 0.26 | 26.95 | 5.39 | 7.33 | 2.30 | 7.68 |
| 嵩山 | 常差检校法 | 45 | 0.44 | 0.15 | 40.43 | 19.04 | 10.59 | 9.25 | 14.06 |
综合分析以上各试验结果可以得出如下结论:
(1) 比较表 1与表 3、表 2与表 4可以看出,采用本文提出的姿态角误差模型补偿后,SPOT-5影像的直接对地目标定位精度几乎达到了像素级水平,而CBERS-02B影像的直接对地目标定位精度由几千米跃升到了几米。两颗卫星遥感影像的直接对地目标定位精度均有了大幅度地提高,这说明本文提出的姿态角系统误差检校方法是有效的,且具有一定的普适性。
(2) 比较图 1与图 2可以发现,无论是SPOT-5影像还是CBERS-02B影像,本文提出的姿态角系统误差检校模型均能较好地拟合其姿态角误差的变化趋势,且yaw的误差相对较大,pitch的误差次之,roll的误差最小。
(3) 比较表 3中本文方法与姿态角常差检校方法的结果可以发现,即使是对于直接对地目标定位精度很高的SPOT-5影像,本文方法比姿态角常差检校方法更能提高对地目标定位的精度,其最大提高幅度达到了33.7%=(10.98-7.28)/10.98,并且使直接对地目标定位精度提高到了±1.3 像素的水平。
(4) 比较表 4中本文方法与姿态角常差检校方法的效果发现,对于姿态角测控误差较大的CBERS-02B影像而言,本文方法比姿态角常差检校方法提升直接对地目标定位精度的幅度最高可达45.4%=(14.06-7.68)/14.68,绝对定位精度优于±3.5像素。
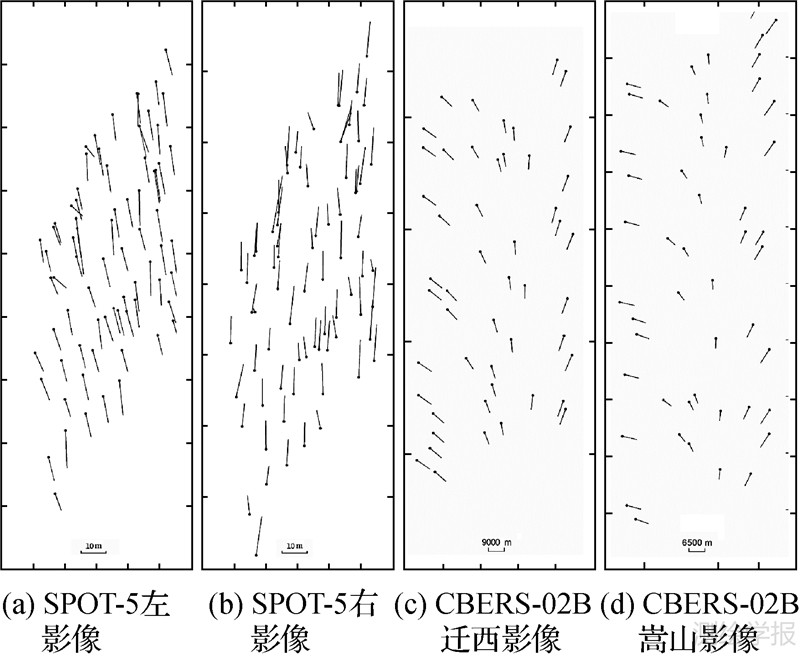
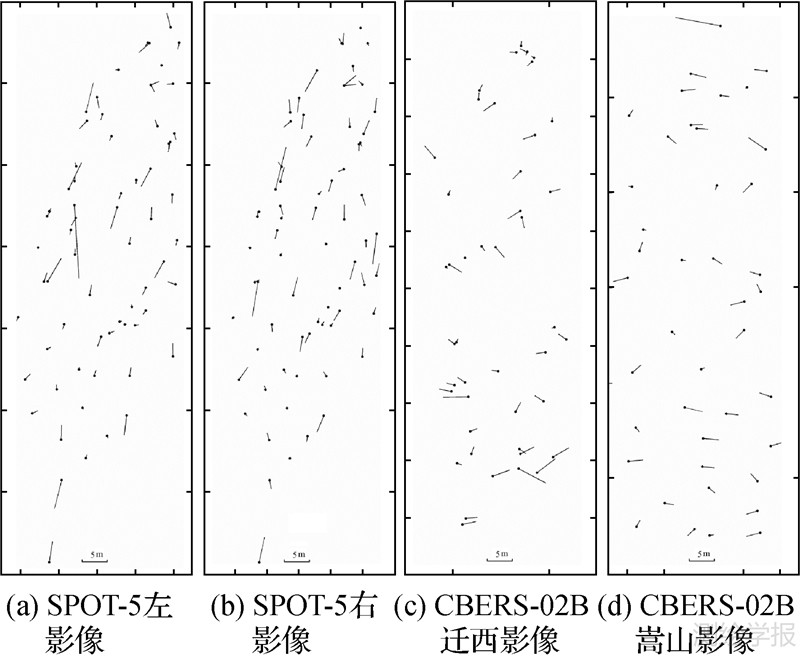
(5) 图 3和图 4分别示意了SPOT-5和CBERS-02B影像利用本文方法进行姿态角系统误差补偿前、后的直接对地目标定位检查点坐标残差分布图。比较图 3和图 4可以发现,利用本文方法进行姿态角系统误差补偿后,两种卫星遥感影像的直接对地目标定位结果已不再存在系统误差了,但CBERS-02B影像的目标定位残差存在少许的跳变现象,这主要是由于TDI CCD的行积分时间跳变所引起的,通过成像时刻t的二次函数就能很好地予以拟合。当有对应的传感器内部CCD排列参数时,还可用分段仿射变换模型来逐步改正。
|
| 图 3 影像姿态角系统误差补偿前直接对地目标定位的检查点坐标残差分布图 Fig. 3 Distribution of residuals of check points in direct positioning before attitude calibration |
|
| 图 4 影像姿态角系统误差补偿后直接对地目标定位的检查点坐标残差分布图 Fig. 4 Distribution of residuals of check points in direct positioning after attitude calibration |
本文提出的影像姿态角误差检校方法比姿态角常差检校方法理论更加严密,充分顾及了传感器运行过程中姿态角误差随成像时刻呈线性变化的特点,这对于高分辨率卫星遥感影像内在几何精度的改善及影像的外推定位是有益的。由于卫星定轨系统测定的是卫星平台的质心位置,其与传感器的投影中心存在相对固定的空间偏移,这一偏移量常常是未知的;而且由于高分辨率卫星遥感成像存在很多物理意义上的几何变形,为了提高影像的直接对地目标定位精度还需要引入更多的几何校正参数,需要很好地解决参数间的相关性,进一步的研究还在继续中。
| [1] | ZHANG Yongsheng, GONG Danchao, LIU Jun. Application of High-resolution Remote Sensing Satellite [M]. Beijing: Science Press, 2004. (张永生, 巩丹超,刘军. 高分辨率遥感卫星应用[M]. 北京:科学出版社, 2004.) |
| [2] | WANG Renxiang. EFP Aerial Triangulation of Satellite Borne Three-line Array CCD Image (Ⅱ) [J]. Science of Surveying and Mapping, 2002 (1):1-7. (王任享. 卫星摄影三线阵CCD影像的EFP法空中三角测量(Ⅱ)[J]. 测绘科学, 2002(1):1-7.) |
| [3] | XU Jianyan, HOU Minghui, YU Jin, et al. Study of CBERS CCD Camera Bias Matrix Calculation and Its Application [J]. Spacecraft Recovery and Remote Sensing, 2004(4):25-29 .(徐建艳, 侯明辉, 于晋, 等. 利用偏移矩阵提高CBERS 图像预处理几何定位精度的方法研究[J]. 航天返回与遥感, 2004(4):25-29.) |
| [4] | ZHANG Guo. Rectification for High Resolution Remote Sensing Image Under Lack of Ground Control Points[D].Wuhan:Wuhan University, 2005.(张过. 缺少控制点的高分辨率卫星遥感影像几何纠正[D]. 武汉:武汉大学, 2005.) |
| [5] | ZHU Xiaoyong, ZHANG Guo, TANG Xinmin. Research and Application of CBRS02B Image Geometric Exterior Calibration [J].Geography and Geo-Information Science, 2009(5):16-18. (祝小勇, 张过, 唐新民. 资源一号02B卫星影像几何外检校研究及应用[J]. 地理与地理信息科学, 2009 (5):16-18.) |
| [6] | JACOBSEN K. Calibration of IRS-1C PAN-camera [C]//Proceedings of ISPRS Workshop on Sensors and Mapping from Space.Hannover:[s.n.], 1997. |
| [7] | TU Xinru, XU Miaozhong, LIU Li. The Geometric Calibration of Airborne Three-line-scanner ADS40 [J]. Acta Geodaetica et Cartographica Sinica, 2011, 40(1):78-83.(涂辛茹, 许妙忠, 刘丽. 机载三线阵传感器ADS40的几何检校[J]. 测绘学报, 2011, 40(1):78-83.) |
| [8] | YUAN Xiuxiao, YU Junpeng. Calibration of Constant Angular Error for High Resolution Remotely Sensed Imagery [J]. Acta Geodaetica et Cartographica Sinica, 2008, 37(1):36-41. (袁修孝, 余俊鹏. 高分辨率卫星遥感影像的姿态角常差检校[J]. 测绘学报, 2008, 37(1):36-41.) |
| [9] | YU Junpeng. Accurate Geometric Positioning of High Re-solution Satellite Remote Sensing Imagery [D]. Wuhan: Wuhan University, 2009. (余俊鹏. 高分辨率卫星遥感影像的精确几何定位[D]. 武汉:武汉大学, 2009.) |
| [10] | POLI D. Orientation of Satellite and Airborne Imagery from Multi-line Pushbroom Sensors with a Rigorous Sensor Model [J]. International Archives of Photogrammetry and Remote Sensing, 2004, 35(B1):130-135. |
| [11] | POLI D. General Model for Airborne and Spaceborne Linear Array Sensors [J]. International Archives of Photogrammetry and Remote Sensing, 2002, 34(B1):177-182. |
| [12] | TOUTIN T. Geometric Processing of Remote Sensing Images: Models, Algorithms and Methods [J]. International Journal of Remote Sensing, 2004, 25(10):1893-1924. |
| [13] | SPOT Satellite Geometry Handbook [DB/OL] [2007-05-10]. http://www.spotimage.fr. |
| [14] | SONG Weidong, WANG Weixi, HU Xinghua. Precise Acquisition of SPOT-5 Exterior Orientation Elements Using Metadata Data File [J]. Bulletin of Surveying and Mapping, 2003(12):29-31.(宋伟东, 王伟玺, 胡行华. 利用Metadata数据文件精确获取SPOT-5外方位元素[J]. 测绘通报, 2003(12):29-31.) |
| [15] | LEI Yutang, LUO Hui, MA Juan. Inherent Errors of the CCD Camera and Their Testing Methods [J]. Optics and Optoelectronic Technology, 2004, 2(4):48-50. (雷玉堂, 罗辉, 马娟. CCD摄像机的误差及其检校[J]. 光学与光电技术, 2004, 2(4):48-50.) |
| [16] | TAO Chuang, LIN Zongjian, LU Jian. Two Dimensional Geometric Calibrations of CCD Cameras [J]. Journal of Wuhan Technical University of Surveying and Mapping, 1993, 18(4):48-55. (陶闯, 林宗坚, 卢健. CCD相机二维几何检校[J]. 武汉测绘科技大学学报, 1993, 18(4):48-55.) |
| [17] | WANG Zhizhuo. Principles of Photogrammetry [M]. Beijing: Publishing House of Surveying and Mapping, 1979. (王之卓. 摄影测量原理[M]. 北京:测绘出版社, 1979.) |
| [18] | ZHANG Jianqing, PAN Li, WANG Shugen. Photogrammetry [M]. 2nd ed. Wuhan: Wuhan University Press, 2010. (张剑清, 潘励, 王树根. 摄影测量学 [M]. 2版. 武汉:武汉大学出版社, 2010. |
| [19] | YU Xiang, YUAN Xiuxiao. Calibration Method of Systematic Errors for CBERS-02B Imagery [C]//Proceedings of the First Symposium on High Resolution Remote Sensing Data Processing and Applications.Xi’an:[s.n.], 2011:76-81. (余翔, 袁修孝. CBERS-02B影像的系统误差检校方法[C]//第一届全国高分辨率遥感数据处理与应用研讨会论文集.西安:[s.n.],2011:76-81.) |
| [20] | HU Fen. Research on Inner FOV Stitching Theories and Algorithms for Sub-images of Three Non-collinear TDI CCD Chips [D]. Wuhan: Wuhan University, 2010. (胡芬. 三片非共线TDI CCD成像数据内视场拼接理论与算法研究[D].武汉:武汉大学, 2010.) |
| [21] | YANG Bingxin. Application of TDICCD in Space Image Sensor [J]. Spacecraft Recovery and Remote Sensing, 1997, 18(3):15-18. (杨秉新. TDICCD在航天遥感器中的应用[J]. 航天返回与遥感, 1997, 18(3):15-18.) |
| [22] | YUAN Xiuxiao. A Novel Method of Systematic Error Compensation for a Position and Orientation System [J]. Progress in Natural Science, 2008, 18(8):953-963. |
| [23] | XU Miaozhong, LIU Li, TU Xinru. Geometric Accuracy Assessment of ADS40 Imagery Using ORIMA [J]. Journal of Geomatics Science and Technology, 2010, 27(5):341-344. (许妙忠, 刘丽, 涂辛茹. 基于ORIMA的ADS40几何精度评估[J]. 测绘科学技术学报, 2010, 27(5):341-344.) |