嫦娥一号探测器(Chang’E-1,CE-1)是中国发射的第一颗环绕月球的探测器,其首要的科学探测目标是获取月球三维影像,制作1∶250万、等高距500m的全月球数字地形图。2007年10月24日18时05分长征三号甲运载火箭将嫦娥一号探测器成功送入太空,拉开了我国深空探测的序幕。CE-1经历了6天环绕地球的调相轨道飞行,于2007年10月31日进入奔月轨道,2007年11月5日被月球重力场捕获,成功进入环绕月球的轨道。北京时间2007年11月20日16时49分,CE-1上的三线阵CCD立体相机开机工作,成功获取了我国第一轨月面图像,2008年7月1日,实现了全月球可见光影像数据的完全覆盖[1, 2, 3]。
2008年7月底,探月工程地面应用系统(由中国科学院国家天文台承建)利用CE-1的CCD立体相机获取的正视影像数据,制作了全月球影像图,并于2008年11月12日正式发布[2, 3]。2009年底,地面应用系统使用CE-1激光高度计获得了912万个激光测高数据,处理得到了空间分辨率为3km的全月球数字高程模型(DEM)[4]。
2009年9月底,地面应用系统利用CCD立体相机获取的三线阵影像数据,制作了全月球数字地形图,并组织召开了评审会,测绘专家、遥感专家、工程技术专家等对该成果进行了鉴定,一致认为该成果在数据覆盖和完整性、平面定位精度、高程精度和空间分辨率均明显好于国际现有全月球数字地形数据,达到了国际领先水平。
CE-1搭载的CCD立体相机能够获得任一月面目标前视、正视和后视3个视角的影像数据,采用卫星三线阵摄影测量的理论和方法[5, 6, 7],可以解算得到月面目标的平面位置和高程信息,从而构建全月球DEM。由于CCD数据的空间分辨率约为120m,远远高于激光高度计测点的密度,采用三线阵摄影测量获得的DEM数据,在数据覆盖、数据精度和分辨率上要远远高于激光高度计获得的地形数据。本论文重点描述了CCD立体相机图像数据摄影测量处理的方法,全月数字地形图的制作过程以及数据结果。
2 CCD立体相机及其图像数据获取CE-1搭载的CCD立体相机由中国科学院西安光学精密机械研究所研制,采用一组光学镜头,探测器为面阵CCD,在面阵上读取沿垂直于飞行方向上的第11行、第512行和第1013行,分别作为前视、正视和后视3个不同视角的影像阵列,相邻线阵之间视角差均为16.7°,每行线阵的像元数为512列,成像谱段为0.5~0.75μm。CE-1的轨道高度约为200km,轨道倾角接近90°,以线阵推扫方式成像,空间分辨率约为120m,幅宽约为60km,在卫星飞行方向上的重叠度为100%,在垂直于飞行方向上,赤道附近相邻轨影像的重叠度约为41%,随纬度的增加,轨间重叠度增大,为月表三维地形几何重建提供了足够的影像信息[8, 9]。表 1列出了CCD立体相机的主要技术和性能参数。
| 指标名称 | 参数值 |
| 帧频帧/s | 11.89 |
| 光谱范围/μm | 0.5~0.75 |
| 光学通道数 | 1 |
| 量化等级/bit | 8 |
| 焦距/mm | 23.33 |
| 线阵像元数 | 512 |
| 像元尺寸 | 14μm×14μm |
| 增益 | 4档可选择(G=1,1.5,3,3.5) |
| 曝光时间 | 4档(3.2ms,7ms,20ms和84ms) |
| MTF | ≥0.2 |
| S/N(ρ=0.2 θ=60°) | ≥100 |
CE-1轨道回归周期为2个月,图像数据的全月面覆盖周期约为28个地球天。由于卫星飞行轨道姿态维持、成像条件的限制和技术试验等统筹安排的原因,在CE-1在轨运行的一年多时间里,CCD立体相机是分阶段开机工作。2007-11-20—2008-05-12陆续完成了月球南北纬70°范围内的图像数据获取,2008-01-04—2008-07-01,完成了月球两极的图像拍摄工作,共获取1000多轨图像数据,实现了图像数据的全月覆盖[1, 2, 3, 4]。
3 三线阵图像数据的摄影测量处理方法地面站接收到卫星信号后,进行解码、解扰和同步处理,得到原始成帧数据,数据传送到数据预处理系统后,经信道处理、辐射校正、几何校正和光度校正等数据预处理,生成二级标准数据产品[3]。通过数据预处理,消除了由于仪器光、机、电等造成的CCD探测器像元响应不一致的误差,给图像数据添加了月面地理信息,将所有图像数据归一化到相同的成像条件下(太阳入射角i为30°,出射角e为0°,相位角为30°)[3],便于数据的摄影测量处理和全月地形图的制作。
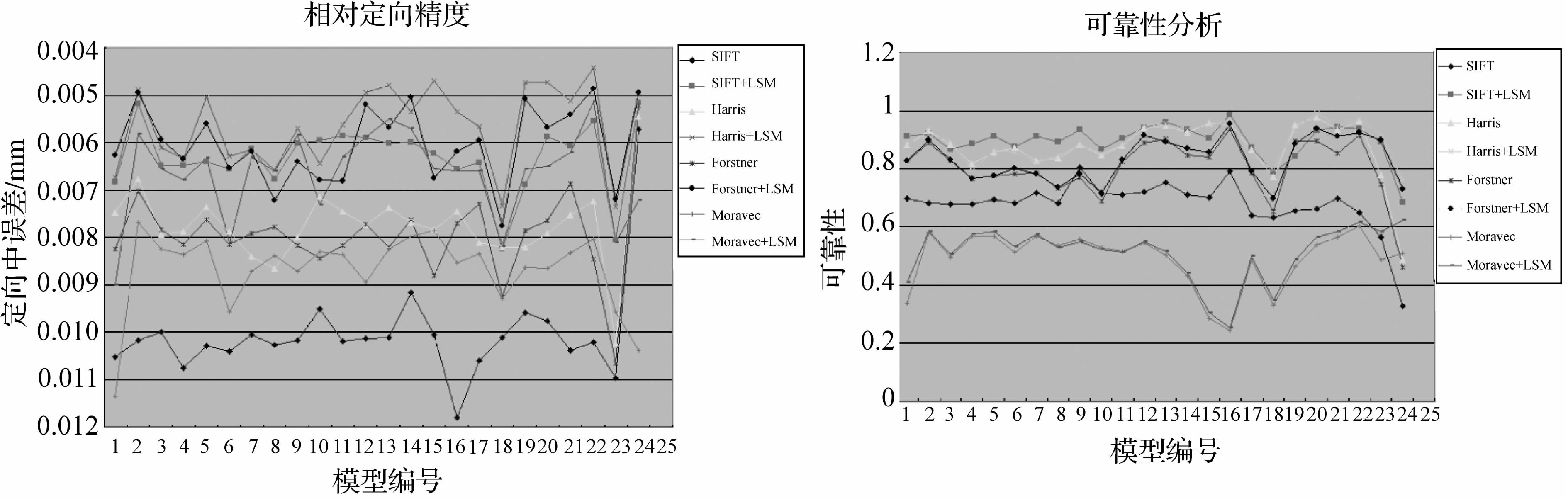
3.1 同名像点的图像匹配处理CE-1三线阵影像的质量情况存在明显的地域性特征,高地图像的亮度、对比度、图像层次和清晰程度等都明显好于月海图像;高纬地区图像清晰、层次丰富,月表地物界限明显,而在低纬与赤道区域,图像质量相对较差[10]。在选取图像匹配算法时,需要充分考虑这种地域性特征。笔者采用24个像对进行了匹配试验,对SIFT、SIFT+LSM、Harris、Harris+LSM、Forstner、Forstner+LSM、Moravec、Moravec+LSM等[11, 12, 13, 14, 15]匹配算法的相对定向精度和可靠性指标进行了比较(见图 1)。
|
| 图 1 各种图像匹配算法对CE-1月球图像的匹配效果比较 Fig. 1 The comparison among CE-1 lunar imagematching effects with different algorithms |
匹配试验表明,Harris+LSM(先使用Harris进行粗匹配,再使用最小二乘进行精匹配)的相对定向精度最好,SIFT+LSM次之。但在可靠性指标上,SIFT+LSM最好,Harris+LSM次之。SIFT特征匹配不仅对图像的尺度变化和旋转具有不变性,对光照的变化和图像变形也具有较强的适应性。因此,笔者选择SIFT+LSM用于CE-1三线阵图像的匹配处理,既保证了同名像点的精度,又减少了误匹配发生的概率。为了保证在月海、充填型撞击坑底部、中低纬度高地等纹理信息匮乏、对比度低的区域获取足够数量的同名像点,采用Canny算子进行加密匹配。对全球202个制图测区进行统计,本文采用的图像匹配算法精度约为0.3个像元。
3.2 三线阵平差处理方法在传统的框幅式像片摄影测量处理中,每张像片上所有像素的外方位元素都是一致的,在两张像片上提取均匀分布的6个或更多的同名像点,利用空间后方交会的方法便可以解算外方位元素[13, 14, 15, 16]。而在CE-1三线阵摄影测量中,用于解算每条线阵外方位元素的这6个同名像点不可能位于同一条扫描行上,从几何条件上无法满足该扫描行外方位元素的解算条件。对于卫星摄影成像,平台较平稳,外方位元素变化不大,文献[5—6,16—17]提出适当增加扫描行的数量,组合成定向片,将航线模型离散化,可以近似地表达航线模型和外方位元素。笔者借鉴定向片法和等效像片(equivalent frame photo,EFP)[5, 6, 7]法的原理,基于独立模型法区域网平差的理论与方法,提出了适用于CE-1三线阵影像数据的平差处理算法。算法原理与步骤如下。
(1) 定向片划分:在正视影像条带上沿着卫星飞行方向每隔50行选择一个定向时刻,以此为中心前后各取80行构成一个定向片,相邻定向片之间重叠率为37.5%。前视、后视图像上相应的定向片边界由图像匹配来界定。定向片上每条扫描行的外方位元素根据相邻定向时刻的外方位元素,通过拉格朗日插值算法计算得到。在平差处理中,定向片被视为近似的面阵影像。
式中,x、y是像平面坐标值(单位为mm);dx为定向片中x方向的图像坐标值(单位为像素);xp、yp为原始图像行、列号;ds=14μm为探测器像元大小;x0=0.8050,y0=-0.7990为像主点的像平面坐标值(单位为像素);L0为扫描线在CCD面阵中的位置(前视L0=11;正视L0=512,后视L0=1013);Li为定向片中心扫描行在影像条带中的行号。通过像片内定向处理,将原始像点的图像坐标值转换为以像主点为坐标原点的像平面坐标值,该坐标值将作为模型相对定向处理的输入数据。(3) 模型相对定向:对构成独立模型的定向片对,通过共面条件建立误差方程,求解每个独立模型的相对定向元素[8, 9],误差方程为
式中,vr为像点残差;F0为根据相对定向元素近似值计算得到的初值;Δφ、Δφ′、Δω′、Δκ、Δκ′为相对定向元素φ、κ、φ′、ω、κ′(ω=0)的改正数;(x,y),(x′,y′)为左右像点的像平面坐标,根据式(1)计算得到;f为相机的焦距。考虑到定向片是一种近似处理,为了提高精度,每个独立模型上选择了约150个均匀分布的同名像点,根据式(2)构建误差方程,按最小二乘原理解算相对定向参数。(4) 模型坐标计算:在相对定向以后,左右定向片对的旋转矩阵R(φ、ω、κ)和R′(φ′、ω′、κ′)基线长度B均为已知,据此可以计算模型点在模型坐标系下的坐标值[8, 9]。模型坐标将作为绝对定向处理的输入数据。
(5) 区域网平差:将相对定向得到的独立模型作为一个整体进行缩放、平移和旋转,并考虑相邻模型之间的连接情况和月面控制点,通过区域网平差,实现独立模型的绝对定向,绝对定向采用七参数变换法[8, 9]。平差试验表明,独立模型在X方向存在明显的线性系统误差。为解决这个问题,笔者在平差算法中对七参数变换公式中的X进行了线性误差修正,增加了修正因子a(式(3))。平差方程如下
式中,a、λ、Φ、Ω、Κ、Xt、Yt、Zt为平差待解算的未知数;Δa、Δλ、ΔΦ、ΔΩ、ΔΚ、ΔXt、ΔYt、ΔZt为其改正数;(X,Y,Z)为模型点的月面摄测坐标,即以测区中心位置为原点的切面坐标系;(U,V,W)为模型点的模型坐标;R(Φ、Ω、Κ)为旋转矩阵;(VX,VY,VZ)为月面坐标残差,[X]、[Y]、[Z]为月面坐标初始值。通过图像匹配确定一定数量均匀分布的相邻定向片的连接点,计算连接点的模型坐标,作为相邻独立模型的连接条件,然后代入误差方程(4),采用最小二乘的方法可解算出绝对定向参数Xt、Yt、Zt、Φ、Ω、Κ、λ和模型坐标改正系数a;式(4)是式(3)线性化的结果。
(6) 测区平差和全球平差处理:本文最终要实现全球所有数据的绝对定向和“无缝”镶嵌,将全月划分为若干区块(即测区),先进行测区平差,再进行全球平差。测区平差和全球平差均采用上述独立模型法区域网平差的方法,唯一的区别是,前者的独立模型是由划分的定向片对构建的地面模型,后者是整个测区对应的地面模型。另外,平差处理必须在控制点的支持下进行[8, 9, 18]。目前存在的月面控制网主要有:阿波罗月面控制网、1994联合控制网(ULCN1994)、Clementine控制网(CLCN1997)、2005联合控制网(ULCN2005)等[19]。这些控制网提供的控制点数据存在很大的缺陷,实际处理中无法使用。因此,处理中平面控制点的初始坐标使用卫星的轨道和姿态数据通过直接前方交会计算求得;高程控制点的高程值从CE1激光高度计制作的空间分辨率为3km的全球DEM数据获取。控制点的精度取决于CE1轨道测量精度[3, 4]。
4 全月地形数据处理与制图
在确定了平差方法后,对CE-1三线阵图像数据进行摄影测量处理,并提取全月球的地形数据。地形数据处理的步骤包括数据组织、图像匹配、测区平差和全球平差等。
4.1 数据组织
CE-1三线阵CCD立体相机总共获得了1000多轨图像数据,筛选其中的628轨,用于全球地形数据的建立。将月球表面划分成若干测区,测区的大小和形状由投影方式、软件处理能力、处理精度、数据覆盖情况等因素决定。全月球表面分为中低纬度(70°S~70°N),南极地区(70°S~90°S)和北极地区(70°N~90°N)3个制图区,每个制图区再划分为若干测区,全球共划分为202个测区,每个测区大约包括20条航带影像。为了保证测区之间的连接条件,裁剪数据时相邻测区在沿经度方向重叠约4°,沿纬度方向重叠约2°。
4.2 匹配处理采用3.1节中的图像匹配算法,提取平差处理和DEM制作中需要的同名像点。共提取了34606761个同名像点用于测区平差处理,23766同名像点用于全球平差处理,291211774个同名像点用于DEM制作。这些同名像点均在数字摄影测量工作站提供的立体环境下进行了人工检查与编辑。相对定向处理结果表明匹配精度约为0.3个像元。
4.3 平差处理按照3.2节中的方法,在相对定向的基础上,先进行测区平差处理,再进行全球平差。平差中用到的相对定向点、模型连接点、航带连接点、测区连接点等,均由图像自动匹配获得。测区平差和全球平差是在月面控制点的约束下进行的。每个测区均匀布设了9个平高点用于测区平差,分别位于在第一轨、中间轨和最后一轨的第一个模型、中间模型和最后一个模型上。全球平差中共选择了211个控制点,其中9个平高控制点均匀分布于全球范围,202个高程控制点分别位于每个测区的中央位置;另外,为了保证相邻测区之间的连接条件,在测区重叠区选择了约23766个连接点。
笔者统计了全球202个测区共约1090800个独立模型相对定向的中误差,最大值为156m,最小值为11m,平均值为42m,中误差超过120m的独立模型个数仅占0.04%,为后续测区平差处理提供了可靠的输入保障;测区平差连接点中误差以测区为单位进行统计,其中误差在X、Y和高程方向的最大值分别为41m(约0.3个像素)、40m(0.3个像素)和110m,实现了测区内所有数据的像素级镶嵌精度,而控制点中误差在X、Y和高程方向的最大值分别为544m(约4.5个像素)、963m(8.0个像素)和472m,可见平差后控制点的位移较大,这主要是由于控制点的位置精度较低造成的;全球平差精度情况见表 2。
| m | ||||||
| 连接点情况 | 控制点情况 | |||||
| X方向 | Y方向 | 高程 | X方向 | Y方向 | 高程 | |
| 最大误差 | 688 | 713 | 462 | 3555 | 3880 | 1727 |
| 最小误差 | 0 | 0 | 0 | 78 | 3 | 2 |
| 平均误差 | 98 | 100 | 93 | 1367 | 1147 | 290 |
| 中误差 | 134 | 137 | 120 | 889 | 1163 | 386 |
| 总点数 | 23766 | 211 | ||||
从表 2可以看出,全球平差连接点的平面中误差为192m(其中,X方向中误差为134m;Y方向中误差为137m),高程中误差为120m;控制点平面中误差为1464m(其中,X方向中误差为889m;Y方向中误差为1163m),高程中误差为386m。另外,相邻测区连接点在X、Y和高程方向的误差最大值分别为688m(约5.7个像素)、713m(5.9个像素)和462m,因此为了实现测区数据之间的像素级镶嵌精度,这些连接点数据还需要进一步处理。
4.4 DEM和DOM制作首先通过图像匹配,在原始图像格网内平均每6像素×6像素提取1个高程点,全球共提取了291、211、774个高程点。然后,利用平差处理得到的相对定向参数、绝对定向参数等,解算每个高程点的月面三维坐标(平面位置与高程值),高程值参考基准面选用半径为1737.4km的正球体表面[20]。最后,采用TIN插值算法,对这些高程点进行插值处理,制作规则格网的DEM数据[21],并利用DEM数据对原始图像进行正射纠正处理,制作DOM数据,DEM和DOM的空间分辨率分别为500m和120m。测区DEM和DOM是以单航带为单位进行处理的,镶嵌处理后得到整个测区的数据,相邻航带接边精度优于240m。
4.5 全球数据镶嵌
由于我国没有小比例尺制图的标准,更没有行星制图的技术规范,因此本文根据美国地质调查局的地图精度标准[22],制作1∶250万、等高距500m的月球数字地形图的平面位置精度要求为850m(1σ),高程精度要求为170m(1σ)。另外,根据CE-1平面制图经验[3],正射影像航带接边、测区接边误差要优于240m(2个像素)的像素级镶嵌精度。
根据表 4和表 5,平面和高程中误差均能满足1∶250万制图要求,但是平面位置最大误差为713m,表明在局部区域正摄影像镶嵌时,仍然会出现3~6个像元的错切,无法达到像素级的镶嵌精度。为了保证正射影像的“无缝”镶嵌,利用全球平差的连接点作为控制点,对每个测区镶嵌后的数据进行了仿射变换,最终镶嵌精度优于240m(两个像素)。数字等高线是利用ArcMap 3D分析工具包提供的等高线提取工具,从全月DEM数据中自动提取,进行人工编辑处理,等高距设定为500m。
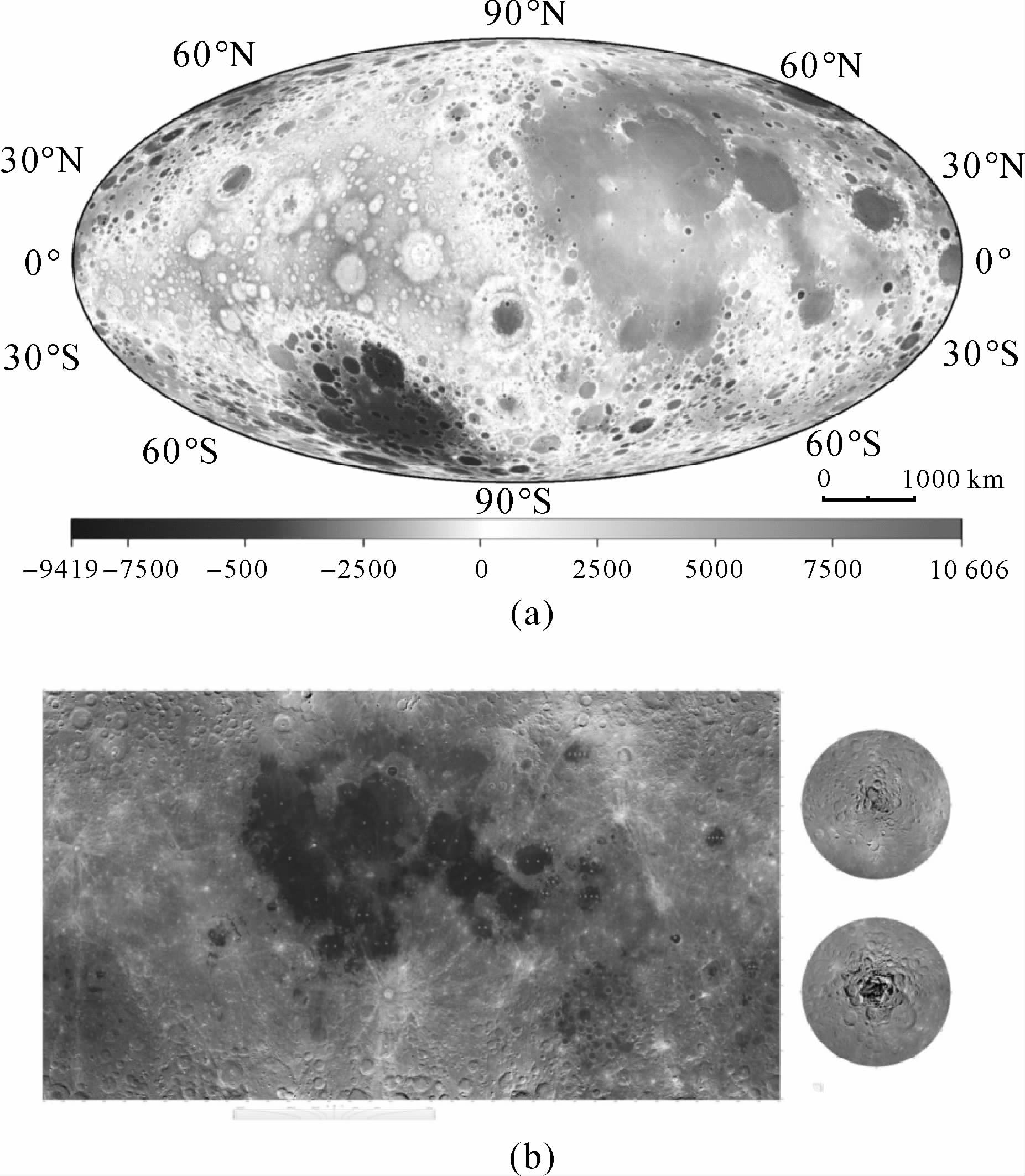
笔者最终完成了比例尺1∶250万、等高距500m的全月球数字地形图的制作,地图的类型包括月球正射影像图(DOM)、月球数字高程模型图(DEM)和月球数字等高线图等,结果见图 2 (a)和图 2 (b)。从图中可以看出,月表地形细节表达层次分明、清晰可辨,能清晰分辨出撞击坑底部、撞击坑或山脉侧壁、月海平面等月面地形特征的详细细节。
图 2 (a)为利用DEM数据制作的彩色晕渲图,空间分辨率为500m,投影方式采用摩尔维德等面积伪圆柱投影,中央经线采用西经270°,左半部为月球背面,右半部为月球正面。图(b)为正射影像图,空间分辨率为120m,图幅左侧为南北纬70°之间的数据,投影方式采用正轴等角割35°墨卡托投影,中央经线采用0°,图幅右侧为月球南极(下部)、北极(上部)区数据,包括南、北纬60°到90°区域,采用等角割70°方位投影。
|
| 图 2 利用嫦娥一号三线阵CCD数据制作的全月球数字地形图 Fig. 2 The lunar global digital topographicmap based on Chang’E-1 data |
为了检验全月球数字地形数据的平面位置和高程的数据精度,一方面,笔者将三线阵平差结果与直接前方交会结果进行了比对,评估平差算法的效果;另一方面,与克莱门汀基础地图(2.0版)[23, 24]、ULCN 2005月面控制网提供的DEM数据(ULCN-DEM)[19]、CE-1激光高度计DEM数据(LAM-DEM)[4, 25]等进行了比较,对地形图平面位置和高程精度进行初步评价。
5.1 与直接前方交会结果的比较在全球范围内相邻航带的重叠区选择了438767个均匀分布的同名检查点,采用直接前方交会和平差的方法分别解算每个检查点的月面坐标,比较同一种方法计算结果的较差。统计结果表明,同名检查点X方向偏差的中误差平差前为265m,平差后为52m,精度提高了约5倍;Y方向偏差的中误差平差前为337m,平差后为50m,提高了约6倍;高程偏差的中误差平差前为267m,平差后为118m,提高了约两倍。由此可见,平差处理使得相邻航带之间数据的连接精度得到了明显改善。
5.2 全月地形图初步评价
要进行绝对定位精度的评价,必须要有可靠、高精度的月面控制点,由于目前没有可靠的月面控制点数据,绝对定位精度的准确评价很难做到。本文选择了目前公开发表的同类数据进行比对,相对、定性地对全月球地形数据作初步评价。
5.2.1 平面位置精度评价使用CE-1全月正射影像图和克莱门汀基础地图(2.0版)[23, 24],在全球均匀地选取1100个检查点,在两幅影像数据上分别量算这些同名检查点的平面位置,计算两者的平面位置偏差(即平面距离)。统计结果表明,CE-1正射影像图相对于克莱门汀基础地图的平面位置偏差最大值为7285m,最小值为217m,平均值为2644m,中误差为2008m。
克莱门汀基础地图(2.0版)是文献[23, 24]以ULCN 2005月面控制网为基础,对Clementine 紫外—可见光相机的图像进行重新定位纠正的结果。ULCN 2005月面控制网发布的平面位置精度约为100m到几千米[19],影像数据的空间分辨率为100m,未经地形校正。根据全球平差结果,CE-1正射影像图的平面位置中误差为192m,空间分辨率为120m,镶嵌误差优于240m(两个像素),经过了严格的地形校正。因此,CE-1正射影像图的月面绝对位置与克莱门汀基础地图存在较大偏差,但相对位置精度明显优于克莱门汀基础地图,并且对月面地形起伏引起的图像几何变形进行了严格纠正。
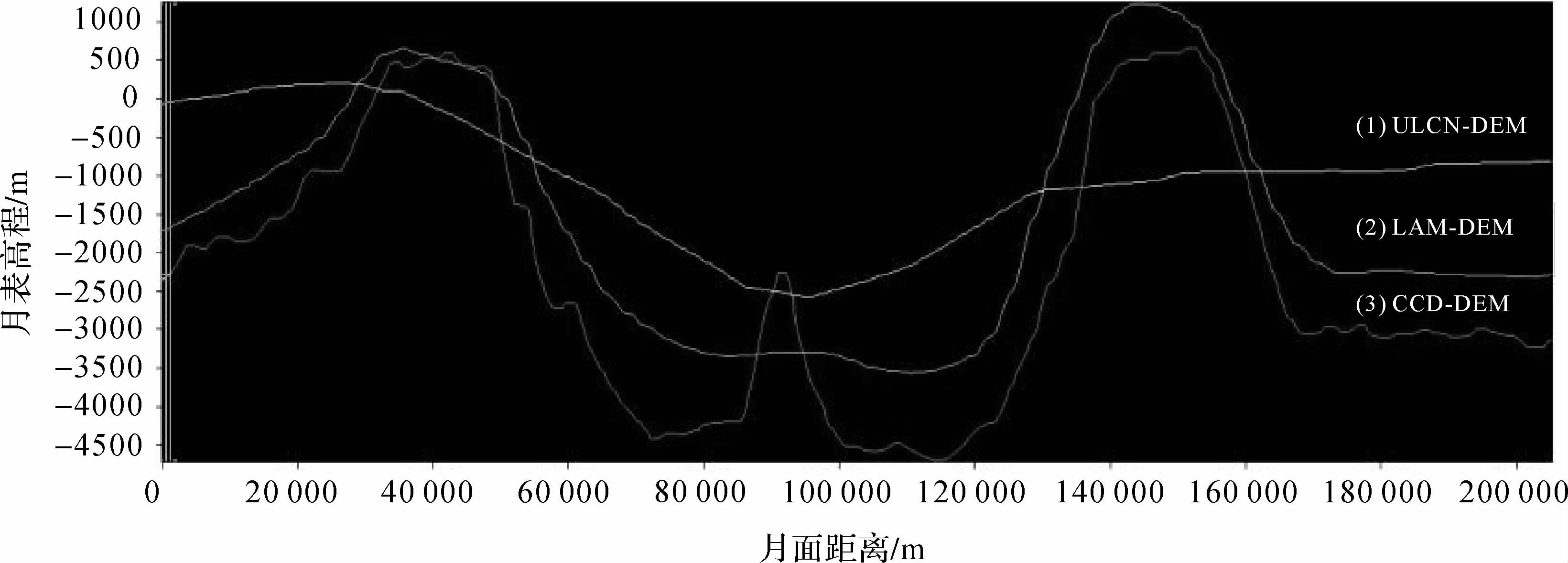
5.2.2高程精度评价分别使用LAM-DEM[4]、ULCN-DEM[19]和全月DEM数据(CCD-DEM),在全球范围内均匀地选择了200个检查点。DEM数据的地形纹理信息的辨别不如图像纹理信息,为了避免DEM检查点位置的人为识别错误,检查点尽量选择在月表平坦地区,如月海地区、撞击坑底部等。在以上3种DEM数据上分别量算同名点的高程信息,计算高程偏差(表 3)。另外,选择了第谷坑、危海、艾特肯盆地东侧等几个典型地貌单元,根据CCD-DEM、LAM-DEM和ULCN-DEM高程数据分别绘制地形剖面线,对月表地形细节表达方面进行对比(图 3)。
| m | |||
| CCD-DEM与 ULCN-DEM 较差 | CCD-DEM与 LAM-DEM 较差 | LAM-DEM与 ULCN-DEM 较差 | |
| 最大值 | 2020 | 1027 | 2061 |
| 最小值 | -2856 | -1126 | -2422 |
| 平均值 | -468 | -193 | -223 |
| 中误差 | 801 | 263 | 470 |
|
| 图 3 第谷坑CCD-DEM、LAM-DEM、ULCN-DEM高程数据地形剖面线对比 Fig. 3 Elevation data topographic line of section plane comparison |
图 3中横轴为相对于左下点的月面距离,纵轴为月面高程,单位为m,高程参考面为半径为1737.4km的月球正球体表面;CCD-DEM对第谷坑中央锥可以明显识别。
LAM-DEM的空间分辨率为3km,高程精度约为60m(1σ)[4];ULCN-DEM空间分辨率为1.895km,高程精度约为100m(1σ)[19];本文制作的CCD-DEM的空间分辨率为500m,高程精度约为120m(1σ)。CCD-DEM的高程值同LAM-DEM的偏差最小,中误差仅为263m,与ULCN-DEM的偏差最大,中误差达801m。从地形剖面上也可以看出高程偏差存在明显的系统性,CCD-DEM相对于LAM-DEM表达的月表地形略偏低,相对于ULCN-DEM明显偏低。CCD-DEM对月表地形细节的分辨能力最强,能明显分辨出撞击坑底部中央锥、月海与撞击坑底部的细节等月面地形特征,由此可见CCD-DEM的地形分辨精度最高。
6 结 论(1) 本文采用摄影测量的理论与方法,利用CE-1CCD立体相机三线阵图像数据制作了比例尺1∶250万、等高距500m的月球数字地形图,地形数据覆盖了全月球范围,平面位置和高程精度分别为192m(1σ)和120m(1σ)。
(2) 全月数字地形图产品主要包括月球正射影像图(DOM)、月球数字高程模型图(DEM)和月球数字等高线图等。正射影像图的空间分辨率为120m,数据完整,色调一致,图像清晰,层次丰富;数字高程模型图的空间分辨率为500m,数字等高线图等高距为500m,地形细节表达层次分明、清晰可辨,能清晰分辨撞击坑、山脉、月海平面等地形特征的细节。
(3) 月球三线阵影像数据的匹配算法采用SIFT特征匹配和最小二乘匹配相结合的算法,有效地解决了月表图像特别是月海和赤道附近月表图像纹理匮乏、反照率低、对比度低而引起的同名像点匹配差的问题,匹配精度约为0.3个像元。
(4) 平差算法采用三线阵独立模型区域网平差的方法,按照一定的原则将全月球表面划分成202个测区,先进行测区平差,测区内平面位置X方向中误差优于41m,Y方向中误差优于40m,高程中误差优于110m;测区平差后再进行全球平差,平差结果平面中误差为192m,高程中误差为120m。平差后相邻航带数据连接精度得到了显著提高,平面位置精度提高约5倍,高程精度提高约两倍。
(5) 平差处理过程中引入控制点改正误差方程参与平差计算,高程控制信息从CE-1激光计DEM数据上获取,解决了月面上没有高精度月面控制点的问题。
(6) 利用全球平差结果建立了月面控制网,对每个测区镶嵌后的数据进行仿射变换,实现了相邻测区之间的无缝镶嵌,测区之间的平面位置接边误差优于240m。
(7) 全月球数字地形数据在数据覆盖和完整性、平面位置精度、高程精度、空间分辨率、地形细节表达等方面均明显好于国际现有全月球数字地形数据。
| [1] | Lunar and Planetary Research Center, National Astronomical Observatories, CAS. Farewell “Chang’E-1”[J]. Chinese National Astronomy, 2009, 23(04):13-21. (国家天文台月球与深空探测科学应用中心. 送别”嫦娥一号”[J].中国国家天文, 2009, 23(4):13-21.) |
| [2] | OUYANG Ziyuan, LI Chunlai, ZOU Yongliao, et al. The Primary Science Result from the Chang’E-1 Probe[J].Scientia Sinica Terrae, 2010,40(3): 261-280. (欧阳自远,李春来,邹永廖,等. 绕月探测工程的初步科学成果. 中国科学: 地球科学, 2010, 40(3): 261-280.) |
| [3] | LI Chunlai, LIU Jianjun, REN Xin, et al. The Global Image of the Moon by the Chang’E-1: Data Processing and Lunar Cartography[J]. Scientia Sinica Terrae, 2010, 40(3): 294-306. (李春来,刘建军,任鑫,等. 嫦娥一号图像数据处理与全月球影像制图. 中国科学: 地球科学, 2010, 40(3): 294-306.) |
| [4] | LI Chunlai, REN Xin, LIU Jianjun, et al. Laser Altimetry Data of Chang’E-1 and the Global Lunar DEM Model[J]. Scientia Sinica Terrae, 2010, 40(3): 281-293. (李春来,任鑫,刘建军,等. 嫦娥一号激光测距数据及全月球DEM模型. 中国科学: 地球科学, 2010, 40(3): 281-293.) |
| [5] | WANG Renxiang. Satellite Photogrammetric Principle for Three-Line-Array CCD Imagery [M]. Beijing: Surveying and Mapping Press,2006. (王任享. 三线阵CCD影像卫星摄影测量原理[M]. 北京:测绘出版社, 2006.) |
| [6] | HOFMANN O, NAVE P, EBNER H. DPS-A Digital Photogrammetric System for Producing Digital Elevation Models(DEM) and Orthophotos by Means of Linear Array Scanner Imagery [J]. International Archives of Photogrammetry and Remote Sensing, 1982, 24(B3):216-227. |
| [7] | LIU Jun, ZHANG Yongsheng, FAN Yonghong. The Photogrammetric Processing and Applications of The ADS40 Airborne Digital Sensor[J]. Journal of Institute of Surveying and Mapping,2002, 19(3):186-188. (刘军,张永生,范永弘. ADS40机载数字传感器的摄影测量处理与应用[J]. 测绘学院学报,2002, 19(3):186-188.) |
| [8] | ZHANG Zuxun, ZHANG Jianqing. Digital Photogrammetry[M]. Wuhan: Wuhan University Press, 2002. (张祖勋,张剑清. 数字摄影测量学[M]. 武汉:武汉大学出版社,2002.) |
| [9] | WANG Zhizhuo. Principle of Photogrammetry[M]. Wuhan: Wuhan University Press, 2007. (王之卓. 摄影测量原理[M]. 武汉:武汉大学出版社, 2007.) |
| [10] | OUYANG Ziyuan. Introduction to Lunar Science[M]. Beijing: China Astronautic Publishing House, 2005. (欧阳自远.月球科学概论[M]. 北京:中国宇航出版社, 2005.) |
| [11] | HIPKE C, SCHMIDT R, BRAND R, et al. Performance of Automatic Tie Point Extraction Using HRSC Imagery of the Mars Express Mission[J]. International Archives of Photogrammetry and Remote Sensing, 2004,35(B4):846-851. |
| [12] | HARRIS C, STEPHENS M.A Combined Corner and Edge Detection[J]. Proceedings of ISPRS Intercommission Conference on Fast Processing of Photogrammetric Data,1987: 281-305. |
| [13] | FORSTNER W, GULCH E. A Fast Operator for Detection and Precise Location of Distinct Points, Corners and Centres of Circular Features[J]. Proceedings of the Fourth Alvey Vision Conference ,1988: 147-151. |
| [14] | LI Jian, LIU Fengde, ZHAO Liping, et al. Best Feature Point Matching Method Research and Application in Automatic Relative Orientation[J]. Science of Surveying and Mapping, 2010, 35(4):84-86. (李健, 刘凤德, 赵利平, 等. 相对定向中最优特征点匹配算法的研究与应用[J],测绘科学, 2010, 35(4):84-86.) |
| [15] | DAVID G L. Distinctive Image Features from Scale-invariant Keypoints[J]. International Journal of Computer Vision, 2004,60 (2): 91-110. |
| [16] | ALBERTZ J, ATTWENGER M, BARRETT J, et al.HRSC on MarsExpress—Photogrammetric and Cartographic Research[J]. Photogrammetric Engineering and Remote Sensing, 2005,71(10):1153-1166. |
| [17] | LI Deren, ZHAO Shuangming, LU Yuhong, et al. Combined Block Adjustment for Airborne Three-line CCD ScannerImages[J].Acta Geodaetica et Cartographica Sinica, 2007,36 (3): 245-250. (李德仁,赵双明,陆宇红,等. 机载三线阵传感器影像区域网联合平差[J],测绘学报,2007,36 (3): 245-250) |
| [18] | XING Shuai, XU Qing, LIU Jun, et al. Bundle Block Adjustment with Multi-source Satellite Remote Sensing Images[J].Acta Geodaetica et Cartographica Sinica,2009,38 (2): 125-130. (邢帅, 徐青, 刘军,等. 多源卫星遥感影像的光束法区域网平差[J].测绘学报,2009,38 (2): 125-130.) |
| [19] | DAVIES M E, COLVIN T R, MEYER D L, et al. The Unified Lunar Control Network: 1994 Version[J]. Journal of Geophysical Research,1994, 99(E11):23211-23214. |
| [20] | SEIDELMANN P K, ABALAKIN V K, BURSA M, et al. Report of the IAU/IAG Working Group on Cartographic Coordinates and Rotational Elements of the Planets and Satellites: 2000[R].[S.l.]: Celestial Mechanics and Dynamical Astronomy, 2002, 82:83-110. |
| [21] | ZHOU Qiming, LIU Xuejun. Digital Terrain Analysis[M]. Beijing: Science Press, 2006. (周启鸣,刘学军.数字地形分析[M].北京:科学出版社, 2006.) |
| [22] | ESTES J E, DOYLE F J. The Remote Sensing Manual:6[M]. Beijing: National Defense Industry Press, 1983. (约翰·E.埃斯蒂斯,弗雷德里克·J.多伊尔.遥感手册:第六分册[M].北京:国防工业出版社,1983.) |
| [23] | HARE T M, ARCHINAL B A, BECKER T L, et al. Clementine Mosaics Warped to ULCN 2005 Network[R].39th Lunar and Planetary Science Conference. Huston: Lunar and Planetary Institute,2008. |
| [24] | LEE E M, GADDIS L R, WELLER L, et al. A New Clementine Basemap of the Moon[R]. 40th Lunar and Planetary Science Conference. Huston: Lunar and Planetary Institute, 2009. |
| [25] | ZHAO Shuangming, LI Deren, MU Lingli. Inconsistency Analysis of CE-1 Stereo Camera Images and Laser Altimeter Data[J]. Acta Geodaetica et Cartographica Sinica, 2011,40(6): 751-755. (赵双明,李德仁,牟伶俐. CE-1立体相机影像与激光高度计数据不一致性分析[J].测绘学报, 2011, 40(6): 751-755.) |