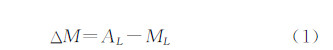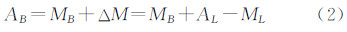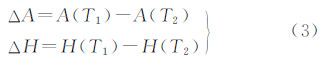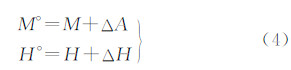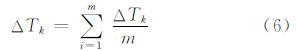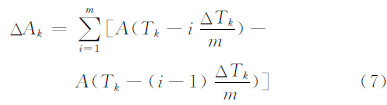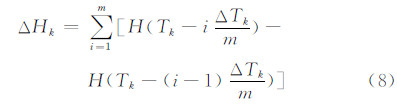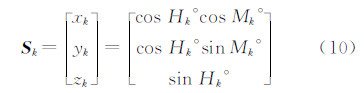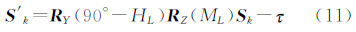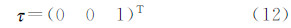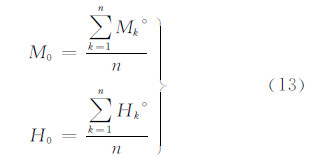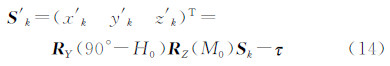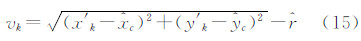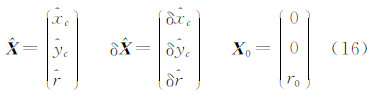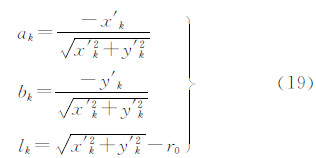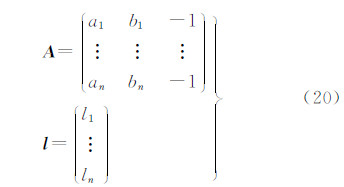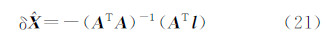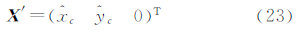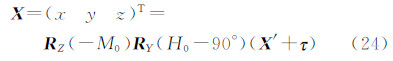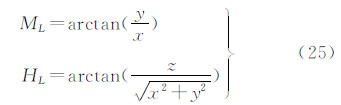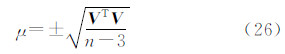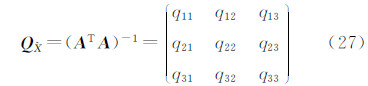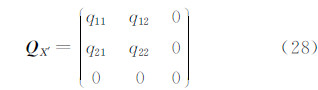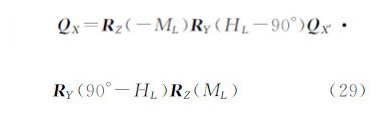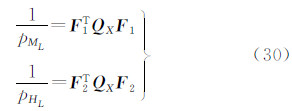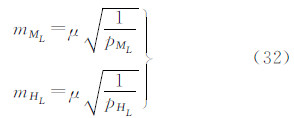2．92003部队，广东 湛江 524037
2. 92003 Troop, Zhanjiang 524037, China
1 引 言
天文定向是依靠天空中的自然天体测定真北方向的一种技术，因其精度较高且是一种绝对定向手段，常用于测定大地网中起始边的拉普拉斯方位角，以控制角度观测误差的累积和传播[1, 2]。又因其具有隐蔽性好、不易受干扰和独立性强等优点，可为航天器发射、远程火炮精确打击、陀螺标校等提供真北基准[3, 4, 5]。目前，夜间天文定向多采用观测恒星进行，但在云雾天气下恒星的可见性极低，往往无法完成定向[6]。月球是天空中除太阳之外最亮的自然天体，可见度要远远高于恒星，是很好的天文定位定向观测目标。
由于视太阳是一个完整的正圆，目前国内已有学者提出利用电子经纬仪观测太阳前后沿进行快速定向，并在实际应用中取得了较好的定向结果[7]。但国内国外尚未有人提出基于电子经纬仪的测月定向理论和方法。这是因为月球有月相的变化，它在绝大部分时间呈现的是一个圆缺面，测日定向的方法无法适用于测月定向。因此，如何利用电子经纬仪确定月球视面中心是定向的关键。基于电子经纬仪对月球边沿观测采样，笔者提出月球视面中心拟合算法，很好地解决了月球视面中心的确定问题，并在实际应用中取得了较高精度的定向结果。
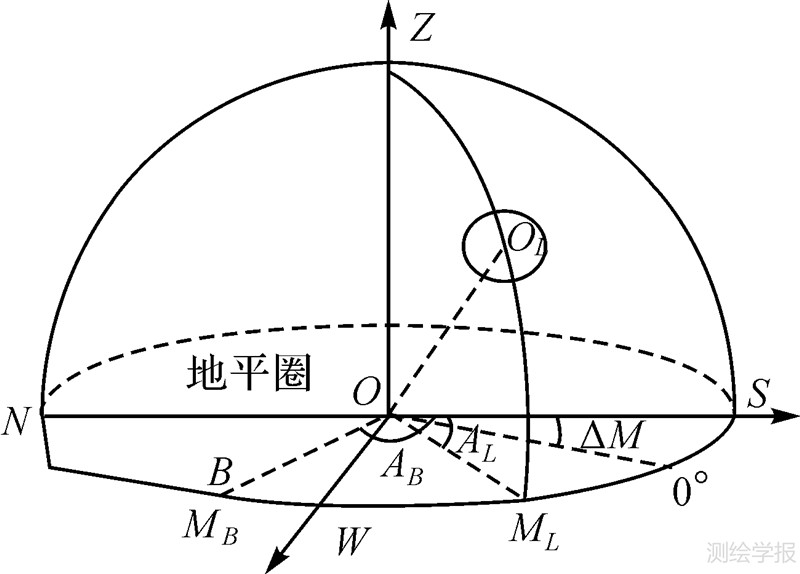
2 测月定向原理 `如图 1所示，O为测站中心，OL为月球视面中心。地面目标B的天文方位角AB是从南点S按顺时针量取至目标的水平角，范围为0°～360°。设在某概略坐标已知的测站，采用电子经纬仪观测地面目标B得到水平度盘值为MB，观测月球视面中心OL得到水平度盘值为ML，同时记录下测瞬时刻T，并用AL表示T时刻月球视面中心的真实方位角。则只需解算出经纬仪水平度盘0°方向与南点S的水平夹角ΔM即可完成定向，即
|
| 图 1 利用月球进行天文定向原理图 Fig. 1 Principle of orientation by observing the moon |
AL需要以观测历元T为引数并借助太阳系天体历表计算得到。IAU 2000年第24届大会推荐太阳系大天体基本历表采用美国喷气推进实验室编制的数值历表DE405，岁差-章动模型采用IAU 2000A模型[8]。为了缩短计算时间，可以采用美国海军天文台提供的NOVAS 2000K岁差-章动模型(488项)代替精确的IAU 2000A模型(1365项)。此时月球视位置计算精度优于3.5mas，完全能满足天文定向的需要[9]。
事实上，月球视面中心无法直接照准观测，即ML不能直接获取，需要一定的观测方法及算法来实现。
3 月球视面中心的确定月球的几何平均扁率约为0.002，目前建立的月球空间参考系中通常将月球看做正球体。由于地月距离较远，可认为地球上观测到的月球是一个很小的圆面，圆面半径约为15′，且圆面中心与月球的质心重合[10, 11, 12, 13]。若利用电子经纬仪对月球明亮边沿进行观测采样，则可获取月球视面的几何信息，利用一定的算法即可解算其中心位置。
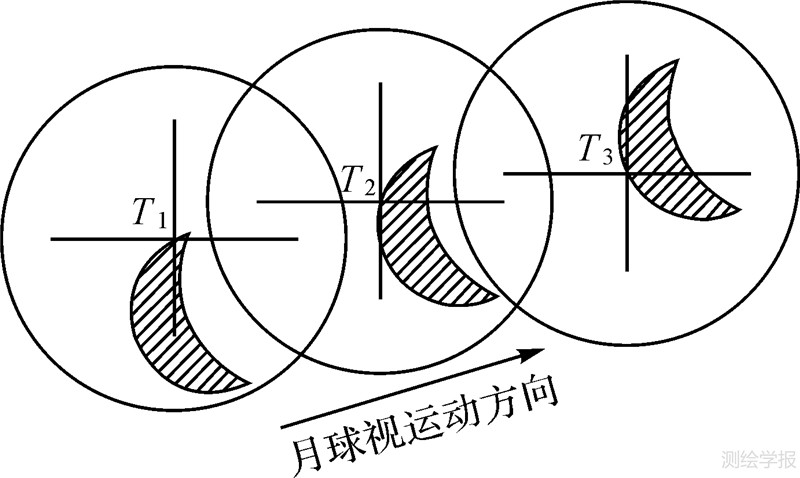
3.1 月球边沿点采样如图 2所示，按照由上至下的顺序，用电子经纬仪望远镜的十字丝中心对月球视面的边沿进行多次均匀采样，记录下每次采样的时刻Tk，水平度盘值Mk和垂直度盘值Hk[14]。确定一个圆，需要知道其圆心坐标及半径，即有3个未知参数，因此至少需要3次采样才能确定月球视面。
|
| 图 2 月球边沿点采样图 Fig. 2 Observing and sampling of the moon edge |
上述采样是在不同历元下进行的，需要将观测数据归算到同一历元。
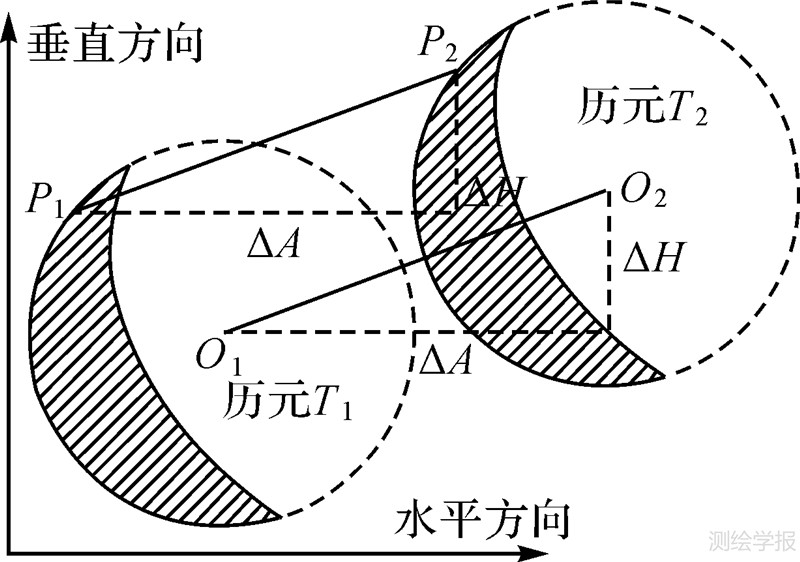
如图 3所示，从历元T1到T2，月球视面中心的位置从O1运动到O2，某采样点的位置从P1运动到P2。如果T1和T2足够接近，可以认为月球在这一时间段内作线性运动，则月球视面中心和采样点的地平坐标变化(ΔA，ΔH)是相同的，可按如下公式计算
|
| 图 3 历元归算原理图 Fig. 3 Principle of epoch unification |
现将第k次采样数据(Mk，Hk)归算到第1次采样历元T1，先令
ΔTk表示第k次采样和第1次采样之间的时间间隔，一般较大，不妨划分为m个等间隔。
显然，只要m足够大，即可认为月球在每一个划分时间间隔内的运动为线性运动，则ΔAk和ΔHk可按如下公式计算。
第k次采样数据归算到历元T1后为
采用此方法，可将所有采样点的观测数据归算到同一历元。归算后的采样点序列可清晰反映月球视面的几何特征。
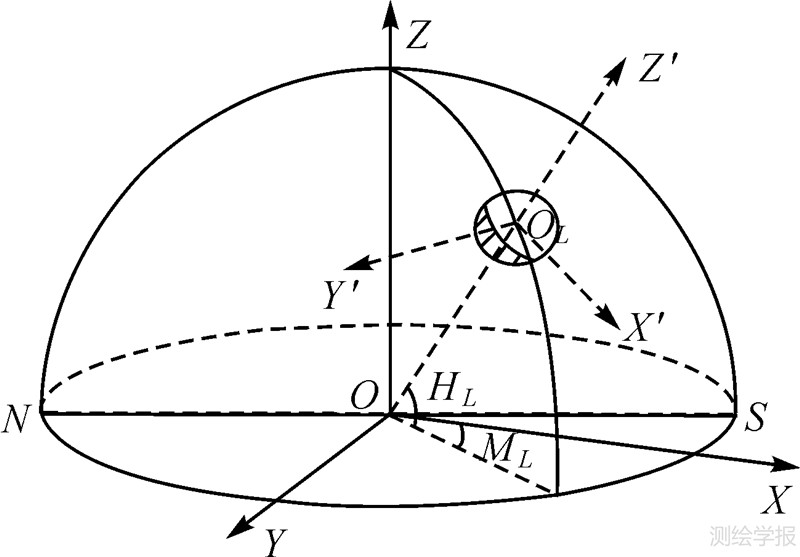
3.3 月面坐标系的建立及转换历元归算后得到的采样数据(Mk °，Hk °)为球面三维坐标，需要转换到月球视面所在的平面直角坐标系下才能进行圆的拟合(图 4)。
|
| 图 4 坐标转换原理图 Fig. 4 Principle of coordinate transformation |
如图 4所示，月球视面中心的水平角ML和高度角HL为待拟合参数。建立坐标系OL-X′Y′Z′，坐标原点OL为月球视面中心，Z′轴在OOL方向上指向天顶，X′轴在垂直面OZOL内与Z′轴垂直且指向天底，Y′轴按左手定则确定，称该坐标系为月面坐标系。再建立OXYZ直角坐标系，坐标原点O设在观测仪器的中心，X轴在水平面上指向水平读盘0°方向，Z轴指向天顶，Y轴按左手定则确定，称该坐标系为仪器坐标系。则(Mk °，Hk °)在OXYZ下的坐标表示形式为
将仪器坐标系转换到月面坐标系，需要先绕Z轴顺时针旋转ML角，再绕Y轴顺时针旋转90°－HL角，最后沿Z轴正向平移1个单位长度即可，用等式表示为[15]
ML和HL 为需要求解的未知参数，但其近似值可通过对采样数据取平均得到，并作为初值。
式(11)变为
(x′k,y′k,z′k)即为月面坐标系下月球视面边沿点的三维坐标。由于月球视面很小，可看做平面，即z′k≈0。因此，只需在OLX′Y′平面内作圆的拟合，即可确定中心。
3.4 最小二乘拟合月面中心假设离散边沿点序列为(x′1,y′1)、(x′2,y′2)、…、(x′n,y′n)，圆心坐标为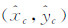
，半径为
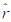，依据几何距离最小的原则，误差方程为[16]
由式(25)计算出的(ML,HL)要比初始值(M0,H0)精确得多，替换初始值，再次进行坐标转换及最小二乘拟合，依此迭代，直至相邻2次计算结果相差较小时为止。实际计算表明，这一迭代过程收敛极快，一般只需2次迭代即可使结果收敛到0.1″以内。
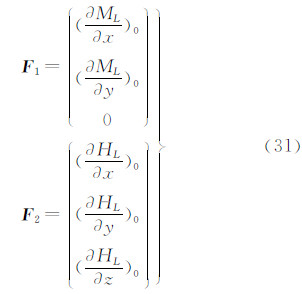
3.5 精度估计单位权中误差μ及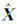
的权逆阵
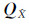表示为
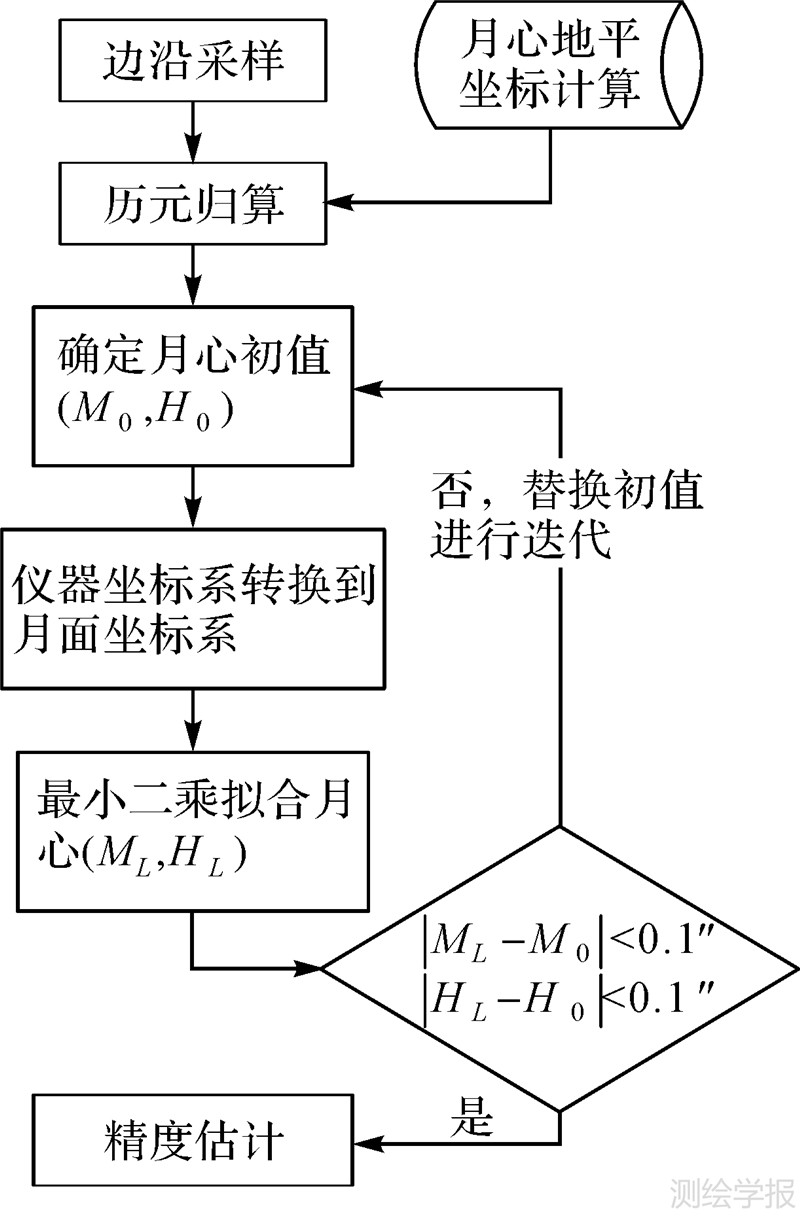
月球视面中心的确定流程如图 5所示。
|
| 图 5 月面中心拟合算法流程图 Fig. 5 Flow chart of the fitting algorithm |
为验证第3节所介绍的月球视面中心拟合算法的可靠性，制定以下试验方案：
(1) 采用北极星任意时角法精确测定经纬仪水平度盘0°方向与南点的水平夹角，作为真值记为ΔM0。
(2) 采用本文介绍的测月方法再次测定上述夹角记为ΔM，以及月球视面中心高度角HL。
(3) 计算水平角的拟合值与真值之差dML=ΔM－ΔM0，高度角的拟合值与真值之差dHL=HL－HL0。dML、dHL可反映月心拟合的外符合精度，内符合精度可按式(32)计算。
(4) 重复步骤(2)、(3)，进行多个时段的观测、计算和比较。
2011年7月16日夜晚，在中国华北地区，月球明亮且光滑的边沿大约只有半个圆周。在某固定测站(天文坐标λ=7h34m29.8s，φ=34°44′22.7″)，采用TM5100电子经纬仪按照上述试验方案进行了多次观测试验，表 1列出了某次测量结果。
| 时段 | dML(″) | mML(″) | dHL(″) | mHL(″) |
| 1 | 1.3 | 2.7 | -4.8 | 1.0 |
| 2 | -0.3 | 2.7 | -3.4 | 1.0 |
| 3 | -0.6 | 3.0 | -1.9 | 1.1 |
| 4 | 1.7 | 1.6 | -2.0 | 0.6 |
| 5 | 1.1 | 2.5 | -3.9 | 0.9 |
| 6 | 4.0 | 3.1 | -4.4 | 1.1 |
| 平均值 | 1.2 | 1.1 | -3.4 | 0.4 |
上述每个时段对月球边沿的采样次数均为12次，拟合得到的月球视面中心的水平角ML与真实值最大偏差为4.0″，最小偏差为-0.3″，平均偏差为1.2″，拟合中误差为±1.1″；拟合得到的月球视面中心的高度角HL与真实值最大偏差为-4.8″，最小偏差为-1.9″，平均偏差为-3.4″，拟合中误差为±0.4″。
高度角偏差普遍较大，这可能是采用标准大气折射改正模型时，没有考虑实际观测时的温度、气压、湿度等因素的影响，造成高度角的改正存在系统差；水平角中误差明显高于高度角中误差，这是因为采样时月球只有左侧边沿明亮且光滑，采样点大致在水平方向上对称分布[18]。总体来看，采用本文介绍的月心拟合算法可较精确地确定月面中心。
5 实际应用参照北极星任意时角法定向的观测方法，制定一个时段内的测月定向观测纲要为[19]：
(1) 观测地面目标。用望远镜的纵丝连续照准地面目标3次，每次照准后记录下水平度盘读数。
(2) 观测月球。对月球视面明亮且光滑的边沿进行顺序采样，采样点要尽量分布平均，采样次数依边沿的长短而定，一般不少于10次。
(3) 纵转望远镜。再观测月球，观测要求同(2)。
(4) 观测地面目标，观测要求同(1)。
重复上述步骤，进行多个时段的观测。各个时段地面目标天文方位角的解算方法和精度估计方法可参照北极星任意时角法定向，这里不再赘述。2011年10月7日在华北地区某固定天文基线(方位角AB=332°58′45.7″，基线长度l=110 m)，进行了5个时段的测月定向试验，结果如表 2所示。
| 时段 | 天文方位角 | 中误差 | 与准确值之差 |
| 1 | 332°58′46.8″ | ±2.0″ | +1.1″ |
| 2 | 332°58′48.2″ | ±2.3″ | +2.5″ |
| 3 | 332°58′48.9″ | ±2.2″ | +3.2″ |
| 4 | 332°58′46.6″ | ±2.1″ | +0.9″ |
| 5 | 332°58′46.9″ | ±2.7″ | +1.2″ |
| 均值 | 332°58′47.5″ | ±1.0″ | +1.8″ |
各时段所测地面目标天文方位角的最大中误差为±2.7″，最大互差为2.3″，与准确值最大偏差为+3.2″；5个时段天文方位角平均值为332°58′47.5″，中误差为±1.0″，与准确值偏差+1.8″。可见利用测月进行天文定向可得到较高精度的测量结果。
6 结 论(1) 本文提出的基于最小二乘的月心拟合算法很好地解决了月球视面中心的确定问题，多个时段的拟合精度可优于2.0″。
(2) 将此算法应用于天文定向，观测5个时段耗时约15 min，内符合和外符合精度均优于2.0″，可满足快速定向的需要。
(3) 由于太阳视面也是正圆，且太阳质心与视面中心重合[20]，因此本文介绍的测月定向方法同样适用于测日定向。
| [1] | WEI Ziqing, HUANG Weibin, YANG Jiezhong, et al.Combined Adjustment of Nationwide Astro-geodetic and Space-geodetic Networks[J].Acta Geodatica et Cartographia Sinica, 2000, 29(4): 284-286. (魏子卿, 黄维彬, 杨捷中, 等.全国天文大地网与空间大地网联合平差[J].测绘学报, 2000, 29(4): 284-286.) |
| [2] | CHEN Junyong, YANG Yuanxi, WANG Ming, et al. Establishment of 2000 National Geodetic Control Network of China and It’s Technological Progress[J]. Acta Geodatica et Cartographia Sinica, 2007, 36(1):1-8. (陈俊勇,杨元喜,王敏,等.2000国家大地控制网的构建和它的技术进步[J].测绘学报, 2007, 36(1):1-8.) |
| [3] | ZHANG Hanwei,XU Houze,WANG Aisheng.The Basic Principle of Mensurating Astronomical Longitude, Latitude and Azimuth Angle[J].Science of Surveying and Mapping,2006,31(4):157-160.(张捍卫,许厚泽,王爱生.天文经纬度和天文方位角测定的基本原理[J].测绘科学,2006,31(4):157-160.) |
| [4] | WANG Anguo.Celestial Navigation Technique in the Background of Navigation War[J].Progress in Astronomy,2001,19(2):326-330.(王安国.导航战背景下的天文导航技术[J] .天文学进展,2001,19(2):326-330.) |
| [5] | FANG Jiancheng,NING Xiaolin.Principle and Application of Celestial Navigation[M].Beijing:Beihang University Press,2006:4-9.(房建成,宁晓琳.天文导航原理及应用[M].北京:北京航空航天大学出版社,2006:4-9.) |
| [6] | ZHANG Chao, ZHENG Yong, LI Changhui.Research of Astronomy Orientation by Using the Random Star[J].Science of Surveying and Mapping,2005,30(4): 30-32. (张超,郑勇,李长会.用任意星进行天文定向的研究[J]. 测绘科学, 2005, 30(4): 30-32.) |
| [7] | ZHANG Chao.System-level Development and Application Research on Astronomic Surveying System Based on Electronic Theodolites[D]. Zhengzhou: Information Engineering University, 2009: 151-155. (张超.基于电子经纬仪的天文测量系统及应用研究[D]. 郑州: 信息工程大学, 2009: 151-155.) |
| [8] | XIA Yifei,JIN Wenjing. Impacts of the New Reference System on Astrometry[J]. Progress in Astronomy, 2004, 22(3): 200-207. (夏一飞,金文敬. 新参考系的引入对天体测量学的影响[J].天文学进展, 2004, 22(3): 200-207.) |
| [9] | BANGERT J, PUATUA W, KAPLAN G, et al. User’s Guide to NOVAS Version C3.0[M]. Washington: USA Naval Observatory, 2009: 31-32. |
| [10] | OUYANG Ziyuan.Introduction to Lunar Science[M]. Beijing: China Astronautic Publishing House, 2005:223-225. (欧阳自远. 月球科学概论[M]. 北京: 中国宇航出版社, 2005: 223-225.) |
| [11] | CHEN Junyong, ZHANG Chuanyin, DANG Yamin. Lunar Spatial Exploration, Surveying and Mapping[J]. Acta Geodatica et Cartographia Sinica, 2005, 34(3): 191-192. (陈俊勇, 章传银, 党亚民. 月球航天探测和月球测绘[J]. 测绘学报, 2005, 34(3): 191-192.) |
| [12] | CHEN Junyong. Progress in Lunar Geodesy[J]. Journal of Geodesy and Geodynamics, 2004, 24(3): 1-6. (陈俊勇.月球大地测量学的进展[J] .大地测量与地球动力学, 2004, 24(3):1-6.) |
| [13] | KONG Xiangyuan,LI Jiancheng,GUO Jiming,et al.Determination of Gravitational Constants for Earth and Moon and Geometric Center and Mass Center of Moon[J].Journal of Geodesy and Geodynamics,2006,26(2): 109-114. (孔祥元,李建成,郭际明,等. 地心和月心引力常数及月球形心与质心的确定[J].大地测量与地球动力学, 2006, 26(2): 109-114.) |
| [14] | XIA Zhiguo,ZHANG Chao,ZHENG Yong,et al. An Astronomical Azimuth Measurement System Aided with an Automatic Gyro Total Station[C]// Third International Symposium on Precision Mechanical Measurements: 2. Urumqi:The International Society for Optical Engineering, 2006: 1400-1405. |
| [15] | XU Qifeng.Space Geodesy[M].Beijing:PLA Press,2001:18-23.(许其凤.空间大地测量学[M].北京:解放军出版社,2001:18-23.) |
| [16] | GANDER W, GOLUB G H, STREBEL R. Least-Square Fitting of Circles and Ellipses[J].BIT Numerical Mathematics,1994,34(4): 558-578. |
| [17] | HUANG Weibin.Principles and Applications of the Contemporary Adjustment[M].Beijing:PLA Press,1992:23-27. (黄维彬.近代平差理论及其应用[M].北京:解放军出版社,1992:23-27.) |
| [18] | AHN S J, RAUH W, WARNECKE H J.Least-squares Orthogonal Distances Fitting of Circle, Sphere, Ellipse, Hyperbola and Parabola[J].Pattern Recognition, 2001,34:2283-2303. |
| [19] | State Bureau of Quality and Technical Supervision. GB/T 17943-2000 Specifications for the Geodetic Astronomy[S]. Beijing: Standards Press of China, 2000.(国家质量技术监督局.GB/T 17943-2000大地天文测量规范[S].北京:中国标准出版社, 2000) |
| [20] | ZHANG Chao,ZHENG Yong,MENG Fanyu.Realizing Astronomy Orientation Fast by Surveying the Sun[J].Journal of Geomatics Science and Technology,2007:24(5):344-345.(张超,郑勇,孟凡玉.利用测日实现快速天文定向[J].测绘科学技术学报,2007,24(5):344-345.) |