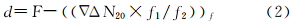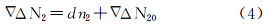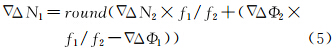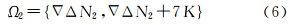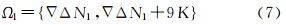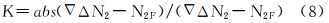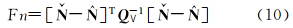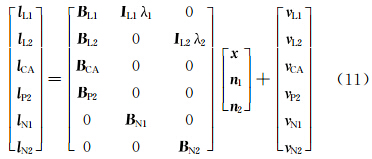Corresponding author: HUANG Dingfa, E-mail: dfhuang@swjtu.edu.cn
1 引 言
整周模糊度的在航解算(OTF)一直以来是国内外GNSS研究的热点问题,受到了广泛关注[1, 2, 3]。文献[4—5]提出LAMBDA算法,能在短时间内完成整周模糊度的分解,实现模糊度的高效搜索。但它对模糊度浮点解的精度有一定的要求,在浮点解精度较差的情况下,LAMBDA固定模糊度所需要的时间会大大增加,甚至导致错误结果。若能提高浮点解的精度,则其固定模糊度所需的观测历元数还可进一步缩减,甚至只利用单历元的观测数据即可固定整周模糊度[6, 7]。为此,不少学者将各类可用的先验约束信息应用到浮点模糊度的解算过程中[8, 9, 10],如姿态确定或定向中,基线长度信息可事先已知[11],某些载体运动轨迹可事先确定[12],或是在形变监测中较为精确的基线信息可由前期的测量得到[13, 14]。基于经验模态分解的基线解算方法在小变形精密形变监测中取得了很好的效果[15]。但这些方法有较强的针对性,使用范围受到较大限制。
文献[16]用双频相位观测值的约束关系进行动态周跳探测修复,对于小周跳有较好的修复效果。基于类似的思想,在可以忽略电离层影响的情况下,本文提出的FirCAR算法可快速解算出高高度角卫星的模糊度。将FirCAR解算的整周模糊度作为已知值重新计算模糊度的浮点解,这类似于增加了毫米级的伪距观测值,模糊度浮点解的精度将会得到改善,且FirCAR解算的模糊度越多,浮点解精度越高,对整体模糊度的固定越有利。本文将FirCAR和常规模糊度搜索算法相结合,充分发挥两者各自模糊度解算的优点,实现在无需其他约束信息的条件下快速初始化定位。最后通过静态和动态情况下的GPS数据验证方法的正确性,分析方法在不同测试环境情况下的有效性,以及FirCAR解算的模糊度个数对基线固定解的初始化时间的影响。
2 GNSS频率间整周关系约束模糊度算法(FirCAR) 2.1 算法基本思想FirCAR充分利用GNSS双频载波相位观测值之间的约束关系,实现高高度角卫星整周模糊度的快速解算。双频观测值可构建如下关系
式中,Φ为相位观测值;f为载波频率;N为整周模糊度;ε∇Δ为双差观测噪声;∇ΔN20为L2载波相位模糊度近似整数值;dn2为∇ΔN20的改正数;e=0或1;下标i代表不同的频率;∇Δ代表双差运算;(x)f代表取x小数部分的运算;round代表四舍五入运算。
FirCAR无需测站位置信息,逐颗卫星进行解算,适用于动态情况下的实时模糊度解算。该方法对高高度角卫星的整周模糊度解算有较高的正确率。以GPS的L1和L2频率为例,当初始模糊度的精度较差时,计算出的GPS整周模糊度可能会在L2上有7周的偏差(从而导致L1上9周的偏差)。另外,FirCAR解算错误的整周模糊度亦会对后面的解算带来负面的影响。采用FirCAR方法进行单历元模糊度解算,卫星截止高度角与解算结果关系如图 1所示,基线1和基线2的长度分别约为3.7km和12.3km。卫星截止高度角越高,由于电离层和多路径的影响减小,解算结果的正确率越高,错误率越低。基线1的解算结果优于基线2,卫星截止高度角大于30°时,基线2解算的错误率才接近于0,其原因在于较长基线的观测值受电离层残差影响更大。
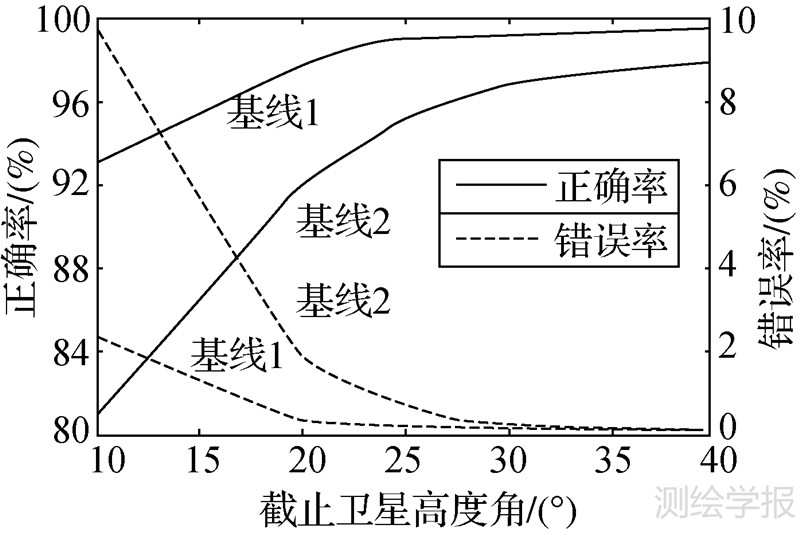
|
| 图 1 截止高度角与解算结果的关系 Fig. 1 Relationship between cutoff angle and resolution |
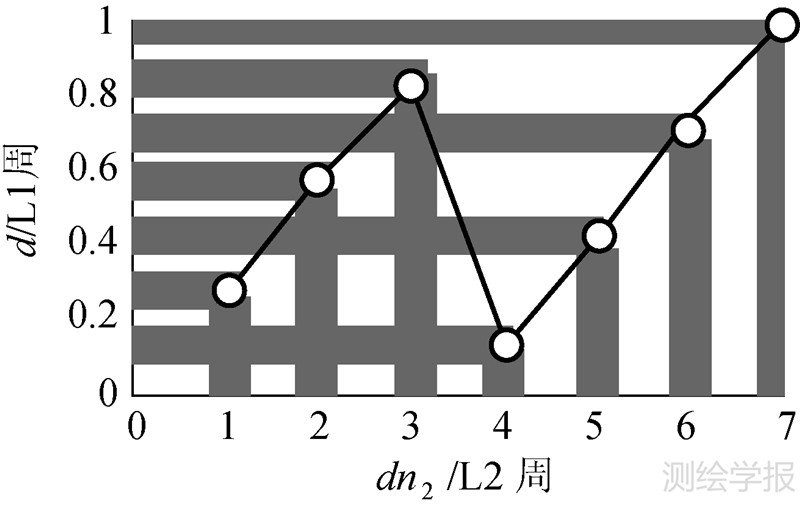
|
| 图 2 模糊度浮点解N2F值精度与dn2候选值个数的关系 Fig. 2 Relationship between the precision of float ambiguity N2F and the number of dn2 candidates |
根据式(3)计算出的dn2值只能是在一个局部的周期内,其周期对应的波长因不同的频率组合而异。表 1列出了几种GNSS频率组合的dn2值局部范围的近似周期关系。
| 星座 | 频率组合 | 近似比例 | 近似周期 |
| GPS | L1/ L2 | 9/7 | 7个L2 cycle |
| L1/L5 | 4/3 | 3个L2 cycle | |
| Galileo | E1/ E6 | 11/9 | 9个E6 cycle |
| E1/ E5a | 4/3 | 3个E5a cycle | |
| GLONASS | G1/ G2 | 9/7 | 7个G2 cycle |
GLONASS卫星G1和G2频率间的比例是9∶7,对应dn2值的周期为G2的7倍。而Galileo的E1和E6频率的近似关系使得对应dn2值局部近似周期为E6的9倍,波长约2.11m。GPS的L1和L2组合的dn2值近似周期为L2的7倍,约1.71m。以GPS的L1和L2频率为例,图 2表示假定L2整周模糊度真值为0时,不同精度的模糊度浮点解N2F所产生的dn2候选值个数的不同。在此不考虑更大的近似周期,因为更大的近似周期将会使得相邻d值的间隔太小而不易区分,见图 3。
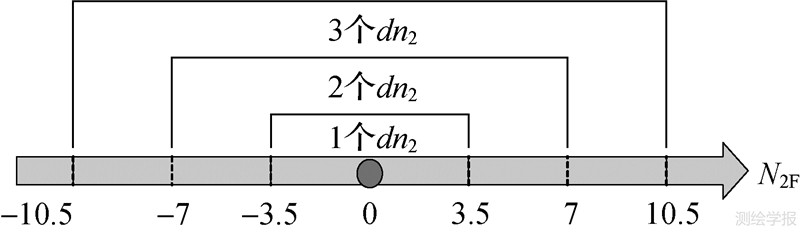
|
| 图 3 一个周期内dn2在d上的投影分布 Fig. 3 dn2 projection distribution on d within a cycle |
若N2F值的误差小于3.5周时,则FirCAR可直接计算出L2和L1的模糊度值,对应模糊度的候选值只有一个,即Ω2={∇ΔN2},Ω1={∇ΔN1}。
若N2F值的误差小于7周,则FirCAR解算的模糊度的搜索空间有两个值,即
若N2F值的误差小于10.5周,为包含正确的模糊度,FirCAR解算的每个模糊度将有3个候选值,每个L2模糊度搜索空间Ω2={∇ΔN2-7,∇ΔN2,∇ΔN2+7},对应L1的模糊度搜索空间Ω1={∇ΔN1-9,∇ΔN1,∇ΔN1+9}。
针对双频GPS接收机,在短基线的情况下,假定L2模糊度初始值N2F的精度优于7周是较合适的,双频GPS接收机一般含有P2观测值,且FirCAR针对的是高高度角卫星的模糊度,观测数据质量相对较好。因此FirCAR方法解算出的n个模糊度(L1的模糊度不需包含在内)的搜索空间有2n个模糊度组合。当观测的卫星数较多时,甚至可认为N2F的误差小于3.5周,此时FirCAR的解算结果只有一个候选值。
特别的,当基线较短且FirCAR解算的整周模糊度大于3个时,亦可根据模糊度之间的内符合精度来判断所解算的模糊度是否正确。此时由于只有流动站的三维测站坐标未知,FirCAR解算出的模糊度个数大于3时,可解算出坐标参数,以及残差或中误差信息。由于各L1和L2模糊度候选值相差9周和7周,在所有的模糊度组合中,可认为中误差最小的一组为正确的模糊度组合。
2.3 错误模糊度剔除方法FirCAR解算结果有较高的正确率,但错误的解算结果无法完全避免。图 1显示了GPS卫星截止高度角与错误解算结果的关系,卫星截止高度角越高,模糊度解算错误的概率越小,高度角大于30°时,错误率接近于0。因此,当判断有错误的模糊度时,可直接剔除FirCAR解算结果中对应卫星高度角最低的模糊度。
图 3显示了一个近似周期内根据d值计算dn2的对应关系,由于相邻的d值对应的dn2相差3周或4周。因此常见的错误是由于计算得到的d值偏离到了其真值所在区间的相邻区间内,从而导致解算错误的模糊度的两个候选值与其真值相差一般为3周和4周。可见解算错误的模糊度的两个候选值偏离真值的大小相近,而解算正确的模糊度的两个候选值却和真值的偏离相对较大,可视为0周和7周,对每颗卫星的模糊度构造如式(9)的检验指标T
式中,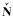 为初始模糊度向量,对应的协因数阵为Q∨;
为初始模糊度向量,对应的协因数阵为Q∨; 为将该卫星的候选模糊度视为已知值重新计算后得到的模糊度浮点解。Fnsec和Fnmin分别表示根据该卫星模糊度候选值和式(10)计算出的Fn值的次小值和最小值。T值越小表明该模糊度的两个候选模糊度精度越接近,它们是解算错误的模糊度的概率就越大。因此,当判断有错误的模糊度时,可视对应T值最小的卫星的模糊度为解算错误的模糊度,将其从FirCAR的解算结果中剔除。
为将该卫星的候选模糊度视为已知值重新计算后得到的模糊度浮点解。Fnsec和Fnmin分别表示根据该卫星模糊度候选值和式(10)计算出的Fn值的次小值和最小值。T值越小表明该模糊度的两个候选模糊度精度越接近,它们是解算错误的模糊度的概率就越大。因此,当判断有错误的模糊度时,可视对应T值最小的卫星的模糊度为解算错误的模糊度,将其从FirCAR的解算结果中剔除。
使用各种约束条件来提高模糊度浮点解的精度是实现OTF快速固定模糊度的一种有效手段,FirCAR所解算出的高高度角卫星模糊度亦是其中的一类约束条件。将成功解算的模糊度视为已知值,等同于观测到了毫米级的伪距观测值,将其增加到观测方程组中,再重新进行解算无疑会提高模糊度浮点解的精度。以常见的双频接收机观测值为例,一个历元的观测数据的观测方程如式(11)
式中,B为对应观测值的系数矩阵;I为单位阵,维数与对应观测值的个数相同;x为基线向量;n1、n2分别为L1和L2模糊度向量;v为对应观测值的改正数;lN1和lN2为虚拟观测值,代表FirCAR方法解算的整周模糊度。采用卫星高度角定权的方式来定权[17],码与相位之间的权比可根据它们之间的标称精度确定,lN1和lN2赋予一个相对较大的权,且远大于其他观测值的权。由最小二乘法可求出模糊度浮点解n和Qn。再结合模糊度搜索方法完成模糊度解算。最后通过ratio指标判断解算结果的正确性,其值常设置为2。
若ratio指标检验失败,则认为FirCAR解算结果含有错误的值,此时根据1.3节的方法剔除FirCAR中错误的模糊度,重新进行模糊度解算。直到FirCAR解算结果中无模糊度,且ratio指标检验失败时,则结合下一个历元的观测数据重新进行解算。算法流程图如图 4。
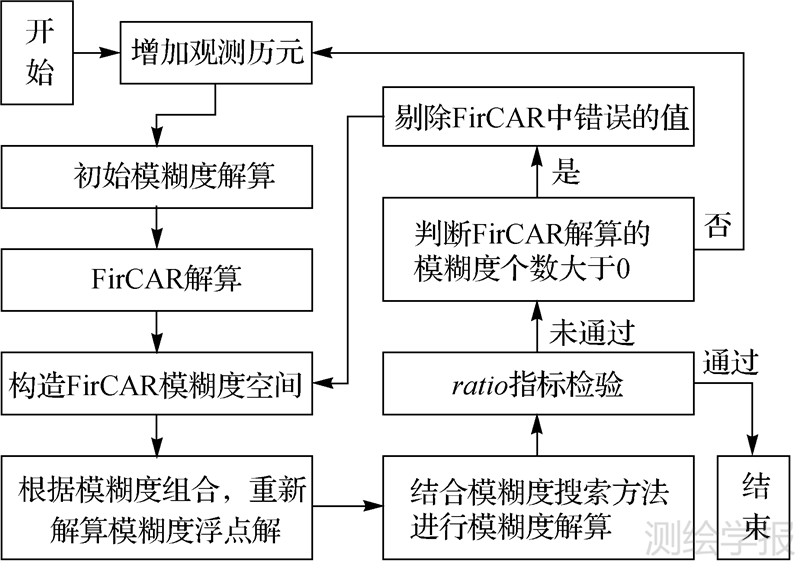
|
| 图 4 算法流程图 Fig. 4 Flow diagram of the proposed algorithm |
试验数据选用IGS上两个相距约3.8km的CORS站的GPS观测数据,数据采样间隔为15s,观测时间长约14h,去掉卫星数小于等于4的观测历元,卫星截止高度角为10°,FirCAR中设置卫星截止高度角为25°。图 5显示了各历元的双差个数和FirCAR解算个数。
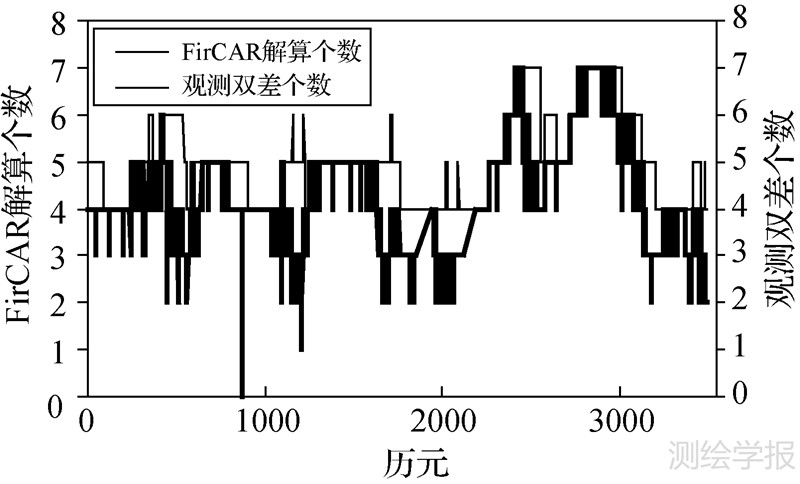
|
| 图 5 FirCAR解算个数和双差观测值数序列 Fig. 5 Series of FirCAR resolved number and numbers of double-difference observation |
针对FirCAR解算个数的不同,设计了6组试验方案,方案1用常规的LAMBDA算法进行模糊度解算,后5组方案采用FirCAR辅助算法,并设置FirCAR解算的模糊度个数最大值分别为1、2、3、4和不限。由于基线较短且其分量信息可事先算得,因此可根据精确的基线信息反算模糊度的值来检验FirCAR辅助算法的正确性。
采用动态模式进行模糊度解算,流程见图 4。模糊度固定后,后续的历元再重复该过程,直到最后。试验统计不同方案中模糊度固定解解算正确和错误的次数,每次模糊度固定所用的观测历元数,以及平均观测历元数等。试验数据总历元数为3334,统计结果见表 2。
| 方案 | 名称 | 正确次数 | 错误次数 | 平均历元数 |
| 1 | 常规算法 | 1919 | 2 | 1.71 |
| 2 | FirCAR辅助算法a | 2348 | 4 | 1.41 |
| 3 | FirCAR辅助算法b | 2588 | 6 | 1.29 |
| 4 | FirCAR辅助算法c | 3035 | 11 | 1.09 |
| 5 | FirCAR辅助算法d | 3197 | 7 | 1.04 |
| 6 | FirCAR辅助算法e | 3198 | 7 | 1.04 |
表 2可以看出,FirCAR算法可减少模糊度固定所用的平均历元数,FirCAR辅助算法(方案6)的平均历元数为1.04,与常规算法相比(方案1)平均历元数减少了约39%,可见FirCAR可提高模糊度浮点解的精度。但模糊度解算错误的个数也有所增加,表 3列出了解算错误的模糊度信息,可以看出错误的解算都发生在只有5颗卫星数的历元内,且只用了1个或几个历元的数据,其他方案也有类似的结论。其原因在于当可用卫星较少时,由于单历元解算多余观测信息少,解算结果的可靠性会降低。因此在卫星观测数较少时,有必要适当增加观测值来验证解算结果的正确性。
| 序列 | 历元 | 卫星数 | 历元数 |
| 1 | 1764 | 5 | 1 |
| 2 | 2050 | 5 | 1 |
| 3 | 2074 | 5 | 3 |
| 4 | 2075 | 5 | 1 |
| 5 | 2118 | 5 | 1 |
| 6 | 3484 | 5 | 1 |
| 7 | 3497 | 5 | 1 |
图 6显示了常规算法(方案1)和FirCAR辅助算法(方案6)模糊度固定所用历元数的频率分布。与常规算法相比,FirCAR辅助算法的模糊度初始化时间更短,其分布的范围小,且分布在1个历元上的频率大。统计结果表明常规算法和FirCAR辅助算法两者模糊度固定所用历元数的最大值分别为25和11,用1、2和3个历元固定模糊度的次数为分别为1276、384、123和3113、72、14,占各自总固定次数的比例分别为66.3%、19.9%、6.4%和97.1%、2.2%、0.4%。
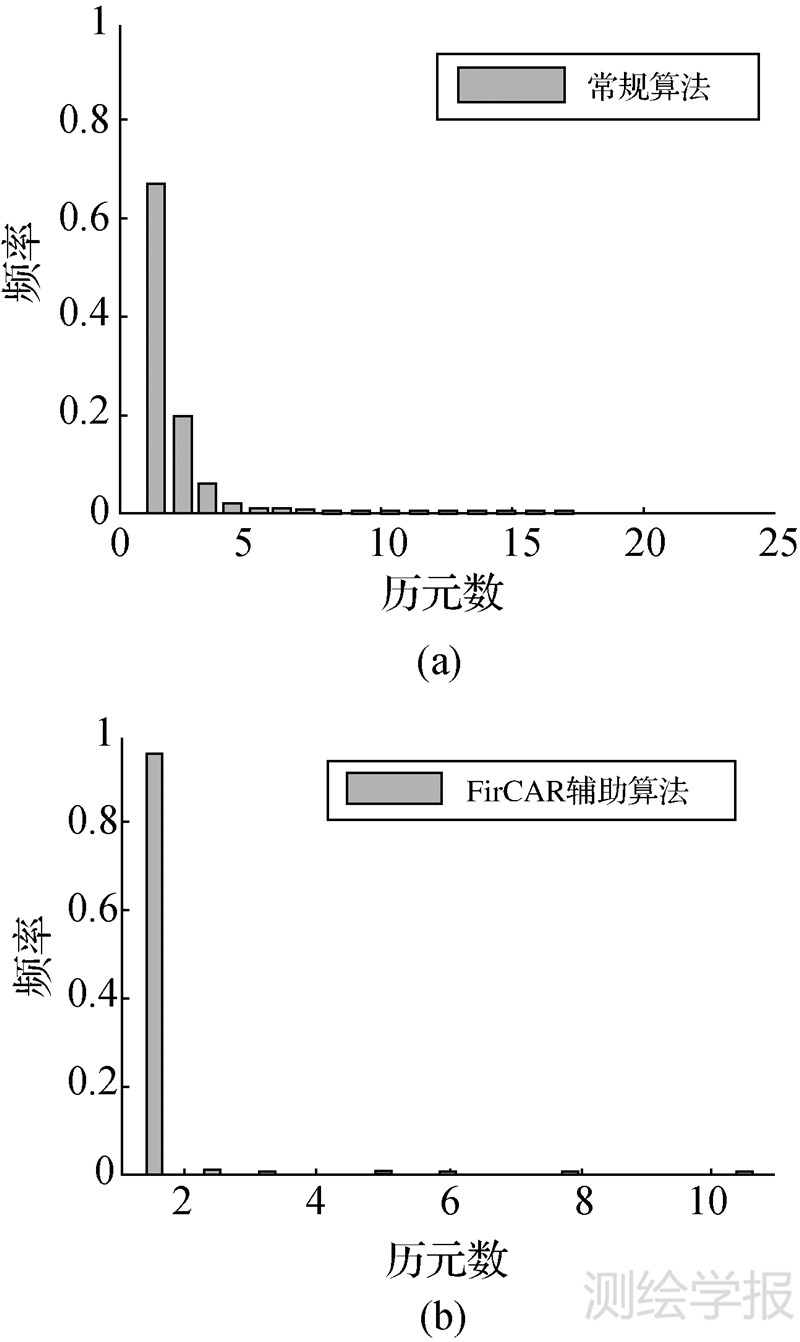
|
| 图 6 模糊度固定所用观测历元数的频率分布 Fig. 6 Frequency distribution of numbers of epochs required to fix ambiguities |
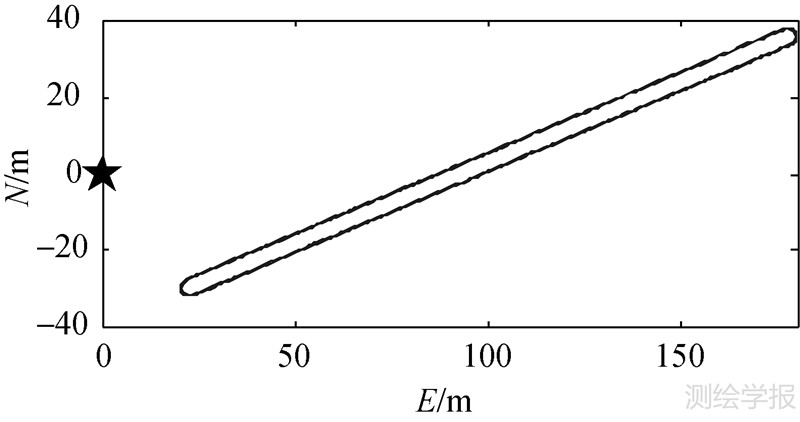
动态试验地点选择在校园内的一个花坛旁边,周边环境相对比较开阔,使用价格较为便宜的双频GPS接收机。采集数据时,参考站接收机放置在旁边,手持流动站GPS接收机围绕花坛行走5周,采用率为1s,卫星截止高度角为10°,总采集约1300个历元,观测到的卫星数保持在7~8颗,参考站位置和流动站的平面运动轨迹如图 7。数据处理过程中,设置FirCAR中卫星截止高度角为25°,且不限制其模糊度解算个数。
|
| 图 7 参考站位置与流动站运动轨迹 Fig. 7 Position of the base station and the rover’s trace |
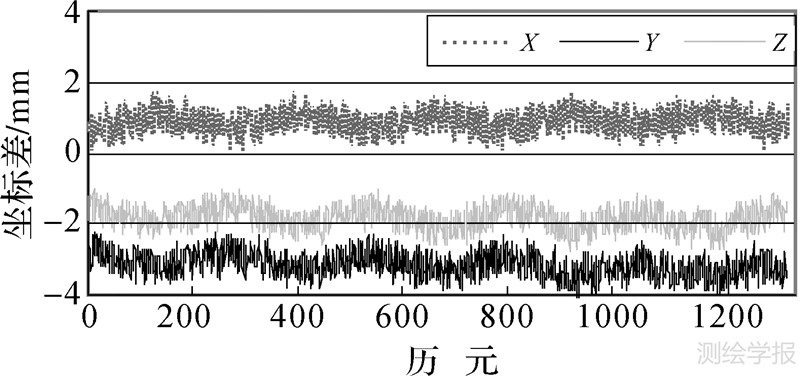
为检验解算结果的正确性,将FirCAR辅助算法的解算结果与GAMIT中TRACK模块[18]解算结果进行比较,空间直角坐标X、Y、Z 3个分量的差值见图 8。可见两种方法计算出的结果的差值均在几毫米范围内,可见本文算法解算的模糊度都是正确的。图 8同时也反映出有系统性偏差,主要是由于两种算法之间的模型不完全相同所造成。
|
| 图 8 与TRACK解算结果的差值 Fig. 8 Differences compared with the solution obtained from TRACK |
图 9对比了FirCAR辅助算法与常规算法模糊度固定所用的历元数,同时还给出了对应历元FirCAR解算的模糊度个数。FirCAR辅助算法与常规算法模糊度固定在最坏情况下所需的历元数分别为11和32,平均所用的历元数为1.10和1.35,固定速度提高了18.5%,两者单历元解算个数分别为1138和808,占各自总数的94%和82.2%。结合FirCAR解算的模糊度个数可看出,当FirCAR的解算个数越大,模糊度固定所需的观测历元数减少越明显。
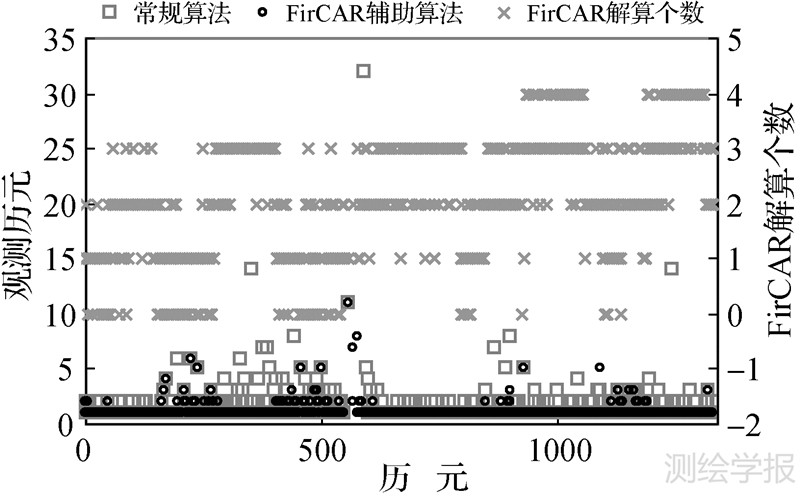
|
| 图 9 2种方法模糊度固定所用的观测历元数 Fig. 9 Numbers of epochs required to fix ambiguities for the two methods |
与图 5的情况相比,动态试验中FirCAR解算个数不如静态试验中的好,一方面在于动态环境中的观测噪声较大,另外,价格较为便宜的接收机观测值质量可能会较差,也可能会影响FirCAR方法。FirCAR可加快模糊度OTF解算的速度,但效果改善程度要比静态的弱。
静态和动态试验结果表明,FirCAR可减少模糊度固定所需的观测历元数,且FirCAR解算出的模糊度越多,后续的模糊度固定所用的观测历元数越少,即模糊度固定的速度越快。
5 结 论(1) FirCAR与LAMBDA算法结合,实现了一种GNSS快速OTF定位方法。静态和动态观测环境下的实测GPS数据的试验结果证明,两种环境下FirCAR辅助算法模糊度初始化所用的平均观测历元分别为1.04和1.10,模糊度固定速度分别提高了约39%和18.5%,实现单历元模糊度固定的比例分别为97.1%和94%,显著提高了OTF模糊度固定的速度。
(2) 静态和动态环境试验结果表明,模糊度固定所用的最长观测历元数,常规算法分别为25和32,而FirCAR辅助算法都为11。可见当模糊度浮点解精度较差时,使用FirCAR方法可明显改善模糊度浮点解的精度,减少模糊度固定所需的观测历元数。
(3) FirCAR解算出的模糊度个数是影响解算速度的重要原因之一,因此当有更多的GNSS卫星可用时,FirCAR的效果将会得到进一步改善。一方面由于模糊度初始解精度的提高可减少FirCAR的搜索空间,另一方面,更多的GNSS卫星还会使得FirCAR解算结果的个数增加。
需要注意的是FirCAR受电离层残差的影响显著,当基线长度为12km时,卫星截止高度角需设置为30°以保证FirCAR有较低的错误率,对于更长基线的模糊度解算FirCAR方法将会受到更大的限制。因此如何通过多频数据来削弱电离层对FirCAR方法的影响将是下一步需要研究的内容。
| [1] | FREI,BEUTLER E G.Rapid Static Positioning Based on the Fast Ambiguity Function Algorithm[J].Journal of Geodesy,1990,15(4):325-356. |
| [2] | CHEN D,LACHAPELLE G.A Comparison of the FASF and Least-square Search Algorithm for on the Fly Ambiguity Resolution[J].Navigation,1995,42(2):371-390. |
| [3] | REN Chao,OU Jikun,YUAN Yunbin.A New Method for GPS Ambiguity Resolution on-the-Fly Using Integer Whitening Filer Search[J].Geomatics and Information Science of Wuhan University,2004,29(11):960-963.(任超,欧吉坤,袁运斌.一种用于GPS整周模糊度OTF求解的整数白化滤波改进算法[J].武汉大学学报:信息科学版,2004,29(11):P960-963.) |
| [4] | TEUNISSEN P J G.The Least-squares Ambiguity Decorrelation Adjustment:A Method for Fast GPS Integer Ambiguity Estimation[J].Journal of Geodesy,1995,70(1):65-82. |
| [5] | TEUNISSEN P J G.The Invertible GPS Ambiguity Transformation[J].Manuscripta Geodetic,1995,20(6):489-497. |
| [6] | QIU Lei,HUA Xianghong,CAI Hua,et al.Direct Calculation of Ambiguity Resolution in GPS Short Baseline[J].Geomatics and Information Science of Wuhan University,2009,34(01):98-104.(邱蕾,花向红,蔡华,等.GPS短基线整周模糊度的直接解法[J].武汉大学学报:信息科学版,2009,34(01):98-104.) |
| [7] | HUANG Dingfa,ZHOU Letao,LI Chenggang,et al.Theory of GPS Augmentation Reference Station Network[M].Beijing:Science Press,2011:98-108.(黄丁发,周乐韬,李成钢,等.GPS增强参考站网络理论[M].北京:科学出版社,2011:98-108.) |
| [8] | PARK C,KIM I,LEE J G,et al.Efficient Ambiguity Resolution Using Constraint Equation[C]//1996:Position Location and Navigation Simposium.Atlanta:IEEE,1996:277-284. |
| [9] | HAN Baomin,OU Jikun.A GPS Single Epoch Phase Processing Algorithm with Constraints for Single-frequency Receiver[J].Acta Geodaetica et Cartographica Sinica,2002,31(4):300-304.(韩保民,欧吉坤.一种附约束的单频单历元GPS双差相位解算方法[J].测绘学报,2002,31(4):300-304.) |
| [10] | LI Bofeng,SHEN Yunzhong.Prior Baseline Information Based Fast GPS Ambiguity Resolution[J].Acta Geodaetica et Cartographica Sinica,2008,37(4):423-427.(李博峰,沈云中.顾及基线先验信息的GPS模糊度快速解算[J].测绘学报,2008,37(4):423-427.) |
| [11] | TANG Weiming,SUN Hongxing,LIU Jingnan.Ambiguity Resolution of Single Epoch Single Frequency Data with Baseline Length Constraint Using LAMBDA Algorithm[J].Geomatics and Information Science of Wuhan University,2005,30(5):444-446.(唐卫明,孙红星,刘经南.附有基线长度约束的单频数据单历元LAMBDA方法整周模糊度确定[J].武汉大学学报:信息科学版,2005,30(5):444-446.) |
| [12] | YUAN Wei,XIONG Yongliang,HUANG Dingfa.A Fast Ambiguity Resolution Algorithm with Track Constraints on Moving Platform[J].Geomatics and Information Science of Wuhan University,2009,34(11):1316-1319.(袁伟,熊永良,黄丁发.附有运动轨迹约束条件的整周模糊度快速分解算法[J].武汉大学学报:信息科学版,2009,34(11):1316-1319.) |
| [13] | XIONG Yongliang,HUANG Dingfa,ZHANG Xianzhou.A Reliable GPS Single Epoch Processing Algorithm with Known Deformation Interval Constraints[J].Geomatics and Information Science of Wuhan University,2001,26(1):51-57.(熊永良,黄丁发,张献洲.一和可靠的含约束条件的GPS变形监测单历元求解算法[J].武汉大学学报:信息科学版,2001,26(1):51-57.) |
| [14] | YU Xuexiang,XU shaoquan,LV Weicai.The Research of Single Epoch Algorithm for the GPS Deformation Monitor Information[J].Acta Geodaetica et Cartographica Sinica,2002,31(2):123-127.(余学祥,徐绍铨,吕伟才.GPS变形监测信息的单历元解算方法研究[J].测绘学报,2002,31(2):123-127.) |
| [15] | WANG Jian,GAO Jingxiang,Wang Jinling.GPS Baseline Solution Based on Empirical Mode Decomposition[J].Acta Geodaetica et Cartographica Sinica,2008,37(1):10-14.(王坚,高井祥,王金岭.基于经验模态分解的GPS基线解算模型[J].测绘学报,2008,37(1):10-14.) |
| [16] | DONG Xinggan,HUANG Dingfa,FENG Wei.Real-time Cycle Slip Detecting and Repairing for Single Station Observation[C]//Proceedings of CPGPS 2010 Navigation and Location Services.Shanghai:[s.n.],2010. |
| [17] | HAN S.Quality-control Issues Relating to Instantaneous Ambiguity Resolution for Real-time GPS Kinematic Positioning[J].Journal of Geodesy,1997,71(7):351-361. |
| [18] | SU Xiaoning,MENG Guojie,HU Congwei.Single Epoch GPS Positioning Based on TRACK Module[J].Journal of Geodesy and Geodynamics,2009,29(3):100-103.(苏小宁,孟国杰,胡丛玮,等.基于TRACK进行GPS单历元定位[J].大地测量与地球动力学,2009,29(3):100-103.) |