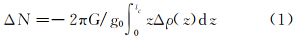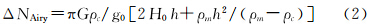2. 武汉大学 地球空间环境与大地测量教育部重点实验室,湖北 武汉 430079
2. Key Laboratory of Geospace Environment and Geodesy of Ministry of Education, Wuhan University, Wuhan 430079, China
1 引 言
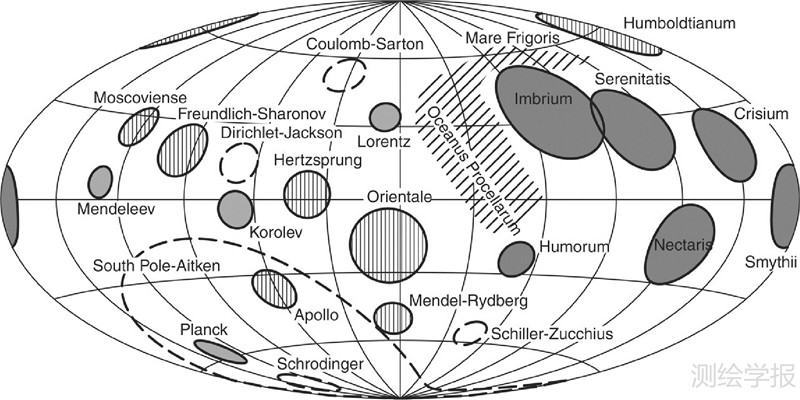
月球的内部构造对于研究月球起源和演化有重要意义。当前确定月球内部结构的方法主要有月震观测[1, 2, 3, 4, 5]和月球重力场反演[6, 7, 8, 9, 10, 11, 12, 13]。根据Apollo月震数据分析结果,月球的内部结构与地球和其他类地行星相似,可以划分为月壳、月幔和月核。不足是测震仪集中在月球正面,无法构建覆盖全球的观测网,而且得到的月壳厚度只能是那些发生月震的有限的离散点。重力异常和地形变化是月球内部密度不均匀和各个界面起伏变化的体现,因此利用重力和地形数据可推定月球岩石圈厚度。文献[6]用Apollo时期近月面的重力与地形数据,引入Airy均衡作为约束条件,利用最小二乘计算了主要撞击盆地的月壳和上月幔模型。文献[7]用Clementine任务数据不考虑玄武岩填充的影响,把布格异常认为仅由月壳厚度变化引起,向下延拓至64km深处的质量薄片,得到一个初步的月壳厚度模型。文献[8]采用文献[7]的方法,并用Parker地形改正快速算法进一步对玄武岩填充对重力的影响作了改正。文献[9]沿用了上述思想,只是在作地形改正和玄武岩填充改正时用了球面坐标公式。文献[10]用日本探月任务更新的重力场和地形模型,采用文献[9]方法,重新计算了月壳厚度模型。以上研究工作把所有的重力异常归因于月壳厚度或密度变化,无疑会使得结果系统性偏大。同时在求取莫霍面起伏时用到了向下延拓,由于其不稳定性,布格异常向下延拓至壳幔边界时,误差成指数增长。文献[11]用100km高处的自由空气重力异常与地形作频谱相关,将其区分为与地形相关和与地形无关两部分。前者和地形重力影响之差就是所谓的均衡地形效应,对应于莫霍面起伏,后者则被认为与月壳下的其他圈层密度异常有关。这种方法顾及了壳下其他圈层的异常效应。
以上研究存在的一个共同的问题是,在计算时引入Apollo 12/14登月点的月震数据得到的60km[1]或55km[2]月壳厚度作为约束,给出一个参考月壳厚度。但近来的重新研究发现Apollo月震网地区的月壳厚度可能更薄:45±5km[3],38±3km[4]以及30±2.5km[5]。而利用水准面与地形之比GTR(geoid to topography ratio)求月壳厚度的一个优点就是不用假设参考月壳厚度。文献[12]用该技术研究了月球高地的均衡和月壳厚度,但没有包括正面的月海区,因为在这些地区重力与地形的导纳为负,求得的补偿厚度将是不合理的负值。文献[13]为避免这个问题,在计算月球Airy均衡厚度之前先去除了质量瘤的影响,但却在南极艾肯盆地(South Pole-Aitken,位置如后文图 3所示,下同)和风暴洋区(Oceanus Procellanum)得到过大的补偿厚度,而在湿海(Mare Humorum)和风暴洋上边缘依然出现了超过100km的负补偿深度,同时在其他月盆地区也没能得出与其他技术相符合的厚度变化趋势。因此,本文旨在用新的更高精度和分辨率的重力场模型SGM100h[14]和地形模型STM359_grid-02[15],去除月海武岩填充,并把与均衡补偿无关的长波和超短波部分(分别对应深层质量异常和表面小尺度地形)剔除,然后再用GTR技术,计算得到一个更符合近来月震研究结果的月壳厚度,为进一步计算岩石圈粘性厚度、月球内部应力分析以及月球演化形成历史研究等提供参考依据。
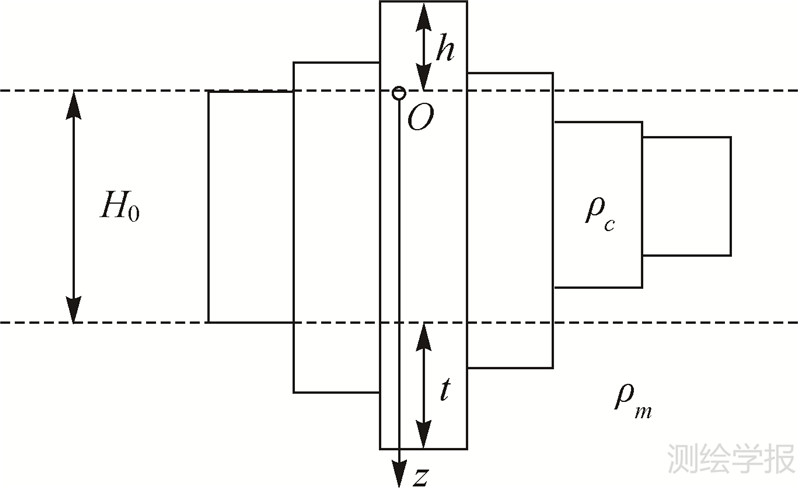
2 均衡补偿模型与月壳厚度目前研究月壳均衡和月壳厚度主要采用的有Airy均衡假说和Pratt均衡假说。文献[16]结合Apollo测高和月球化学数据推测月球近似满足Pratt均衡机制,可以很好地解释月球高地的高度变化,但对于撞击盆地则不适用。文献[12]研究表明月球高地的组成和密度与高度并无明显的关系,认为Pratt均衡不那么重要。因此Airy均衡假说应用更多。在Airy均衡模型中,假设月壳的密度不变,而厚度不同,高地的下面是厚月壳,而月海下则由于月幔的隆升,月壳较薄,如图 1所示:表面地形h对应的“山根”厚度t=ρch/ρm-ρc,其中,ρc是月壳密度;ρm为月幔密度。需要指出的是,在月壳的研究中通常要先去除玄武岩填充,即认为月海玄武岩填充前已处于Airy均衡状态,后来的填充载荷由弹性岩石圈支撑[6]。实际计算表明,去除玄武岩填充后,正面大部分地区均衡度在80%以上,表明可以采用Airy均衡模型。
|
| 图 1 Airy均衡模型 Fig. 1 Airy compensation model |
水准面异常主要是由于内部的密度不均匀和各个界面的起伏变化所造成的。如果表面地形满足均衡补偿,由局部密度异常Δρ引起的大地水准面异常表达式[17]
式中,G为万有引力常数;g0是表面正常重力;tc是异常物质的厚度;z是垂直坐标(向下为正)。令参考月壳厚度为H0,并取其上表面为z轴原点(如图 1所示)。此时异常物质包括两部分:在月球表面,异常物质即是均衡地形h,Δρ=ρc,积分区间 [-h,0];在莫霍面处,异常物质即是山根t,Δρ=ρc-ρm,积分区间 [H0,H0+t]。将其代入式(1)即得由于月壳厚度的变化引起的月球水准面异常
需要指出的是,上述结果只有当表面地形的尺度比月壳厚度要大时才适用。由后文知30阶以内的谐系数与均衡补偿有关,对应的半波长约180km,而平均月壳厚度约40km,最大也不过110km。因此上述公式可用于研究月壳厚度,需要解决的问题是如何提取与均衡有关的重力场和地形信息,将在后文3.2部分论述。
由已知的ΔN、h拟合曲线ΔN=c0+c1h+c2h2。注意到系数c1即是需要的GTR,从而得到GTR与参考月壳厚度H0的关系
表面地形和莫霍面起伏之间的部分就是要求的月壳厚度,即:TT=h*+t+H0。此处h*表示完全的表面地形,与上述均衡地形h有所区别。
3 数据分析与处理 3.1 新的重力场和地形模型月球重力场确定的一个难题是由于月球自转和公转周期相同且同向,从而导致其一直是一面朝向地球,尽管由于月球的天平动和绕月卫星有一定的轨道高度而使得观测覆盖大于一半,但依然有约1/3的背面没有直接跟踪数据。日本Kaguya计划就是为了能得到背面跟踪数据而设计采用高低卫星跟踪卫星模式。同时,其携带的LALT激光高度计可获取覆盖全月面的地形测量数据。由其观测数据得到重力场模型SGM100h和地形模型STM359_grid-02。SGM100h由于有了背面直接观测数据,精度有质的提高。最新给出的经嫦娥一号绕月卫星优化的重力场模型CEGM02[18]在5阶内精度比SGM100h提高约2倍,但在本文研究用到的中短波长范围内差别不大,所以依然采用了SGM100h模型。
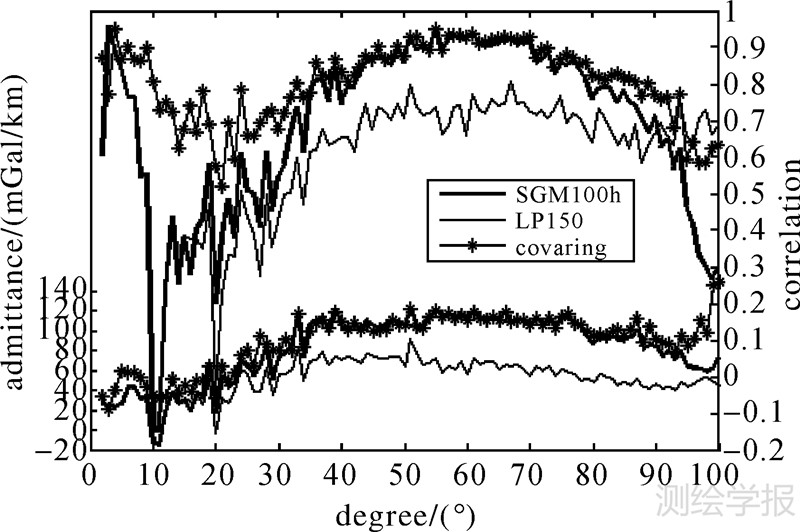
图 2中给出了重力场模型LP150[19]和SGM100h与地形模型STM359_grid-02的导纳和相关性。由图可见:在阶数小于10的部分,地形和重力有较好的相关性,这与艾肯盆地及其周围的高地有关,雨海(Mare Imbrium)和澄海(Mare Serenitatis)也有部分贡献;10、11阶则呈现负相关性,这与月球正面主要的质量瘤有关[20];在17阶后,SGM100h的相关系数明显比LP150更高,尤其LP150在20阶附近的负相关系数在SGM100h中甚至已经为正,这是由于四程多普勒跟踪技术的应用,补充了背面重力场信号。
|
| 图 2 LP150和SGM00h与STM359_grid-02的导纳和相关性 Fig. 2 Admittance and correlation spectra of LP150/SGM00h and STM359_grid-02 |
月球上一个很重要的现象就是质量瘤的存在[21],即通常中间存在大的正异常峰值,而其周围却被负的重力异常所环绕,地形很低且呈盆地状。研究表明质量瘤是地幔高密度物质的沉积和盆地最后的玄武岩填充的共同结果,但究竟主要是哪一部分引起仍需要进一步研究。文献[13]指出,如果不去除质量瘤影响,将使得月海区存在很大的负补偿深度。本文用文献[9]采用的月海玄武岩环形质量薄片模型,对重力场和地形模型施加改正,以消除其影响。文献[20]曾指出:用所有的球谐系数得到的Airy均衡厚度是无意义的,因为Airy模型只是在重力场和地形系数的阶次相关性为正(即所谓的covaring harmonics)时才适用。所以,本文在去掉月海玄武岩填充影响的基础上,剔除那些阶次相关性为负的系数,重新计算其导纳和相关性(图 2带星号曲线)。可看出在40阶以内,特别是在10、11阶本来突然为负的部分,得到明显改善。实际上经过去除玄武岩填充后,已很好地改善了相关性,再剔除相关性为负的系数作用不大。这并不是说Arkani-Hamed的结论不正确,他是在未进行玄武岩填充改正而直接进行的剔除。应该说,这两种方法都很好的起到了质量瘤改正的作用。
地球动力学研究表明:水准面的长波部分很大一部分与地幔内的动力学过程有关,而短波部分才与地形的均衡补偿有关,中长波部分则是二者共同作用的结果,更短波长特征则与弹性支撑有关。因此在利用均衡理论研究月壳厚度时需要去除那些不相关的部分。文献[22]在研究月球表面地形荷载时认为低于17阶的部分主要由薄膜应力作用支撑,而大于17阶的部分由弯曲应力支撑。文献[23]经过重力场频谱分析认为2~5阶部分主要与月幔密度异常有关,6~13阶可能与月壳厚度变化有关,而高于30阶的部分则解释为由弹性岩石圈支撑的非均衡地形引起。考虑到直接的截断可能引起吉布斯振荡,所以设计平滑带通滤波器。该滤波器完全去除5阶及以下部分,6~20阶采用高通滤波,在9阶时滤去60%的信号;20阶以后采用低通滤波,考虑30阶重力场模型对应的半波长约为182km,同时文中研究到的半径最小的席勒坑,半径约165km,所以取平滑半径150km。
将上述处理过的N、h取20°、30°、35°和40°的拟合半径,用最小二乘线性拟合得到实测GTR。当拟合半径较小时,GTR变化较大,当取至30°时,已相当稳定,考虑到向两极格网边长的减小,采用40°的数据。再由式(3)得到H0,从而得到月壳厚度TT。
4 结果分析依据上述分析过程,计算得到滤波前后2个不同月壳厚度模型。在滤波前的Airy均衡月壳厚度图(记为模型1,未给出示意图)中,湿海和劳伦茨坑(Lorentz)之间的风暴洋区出现了比其周围要低的补偿深度,拟合半径较小时甚至为负;上部风暴洋和雨海则出现了达240km的厚度。实际上如果不去除玄武岩填充的影响,月海区域却是更大的负补偿厚度。其在雨海存在过大的正补偿深度,可推断它的高重力异常主要是由月幔抬升引起,所以仅去除玄武岩填充的方法失效。相应的,其他效果较好的月海则可认为其高重力异常与玄武岩填充有关。
在采用了上文所述的滤波策略后,得到一个新的模型——模型2(如图 4),该模型计算得到月壳厚度最薄不到4km,在史密斯海(Mare Smythii)内,最厚106km,在科罗列夫坑(Korolev)北缘。由图可看出,背面月壳厚度明显比正面要厚,在各月盆则存在着中间较薄,四周逐渐增厚的趋势。统计表明:该模型平均厚度36.9km,与Wieczorek等综合给出的49±16km[25]一致;背面平均厚度43.7km,正面平均厚度30.2km,两者相差13.5km,比文献[8—9,11]的12km左右相当;赤道地区40.4km,两极33.5km,相差6.9km,在文献[9]的单/双层的11.8/4.9km之间。
据推测月球在形成初期,表面大部分地区被岩浆洋覆盖;在岩浆洋结晶过程中,Al、Ca、Th和U等元素主要分隔于月壳内[26]。因此平均月壳厚度是推测月球构成成分的一个重要参数。以U元素为例:由Apollo热流量数据分析得到的U含量约19 ppb[27];如果采用平均月壳厚度70km,由其他研究者给出的Th含量间接计算的U含量约39 ppb[5];而如果采用本文结果36.9km,经简单换算,U含量约20 ppb,与上述热流量数据计算结果相当。

|
| 图 4 月壳Airy均衡厚度图(模型2) Fig. 4 Airy isostasy crustal thickness map (model 2) |
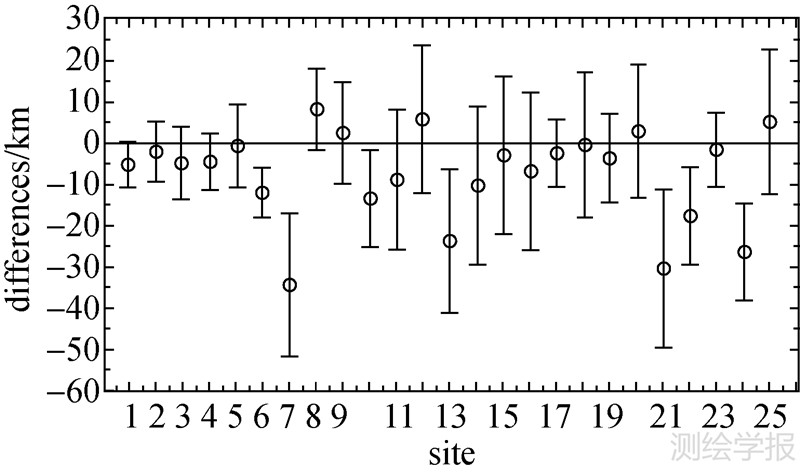
Apollo登陆点安装有月球测震仪,是月球上速度模型确定最精确的区域。本文得到Apollo12/14登陆点的月壳厚度分别是28.3km和29.1km,与新近月震数据重新分析结果30±2.5km[5]一致。文献[26]采用Markov链Monte-Carlo算法反演月震观测数据得到月壳厚度横向变化。图 5给出了本文结果与文献[26]在25个点上月壳厚度的比较。由图可见,除7、13、21、22和24等5个点外,其他各点在不确定范围内与月震数据分析结果较为接近。月震反演得到的上述5个点的月壳厚度较厚,比如点7:61±17km,点24:66±11km,同文给出的重力反演结果本别是30~43km和32~44km。而本文的结果分别是26km和40km。试算显示:如果增加月壳的阻抗比(Vp/Vs=2.0),点7的厚度将降低为40±20km,而其他点几乎没有变化[26]。在厚度图上比对它们的位置将发现:这些点大都位于月幔隆起的边缘,此处月壳厚度由薄到厚的转变较为剧烈,些许的位置变化将导致很大的厚度值改变。而Apollo测震仪集中在月球正面,无法构建覆盖全球的观测网,使得月震发生位置的确定不够精确。所以图中的差异较大各点可归因于位置误差。
如果严格比对二者的差异,由图 5可看出,本文结果较月震分析得到的结果偏薄。可能的原因是使用了简单的Airy补偿模型,去除了过多的“山根”部分,以及在求取水准面高和对应高程时用到的低通滤波以及低阶项的截取,滤掉了过多的信号。库尔特·拉姆贝克曾指出:分层地壳中间不连续面确定很好的情况下使用简单的Airy模型,将使平均补偿深度估计不足[28]。因此,本文得到的较薄模型,并不一定表示Airy均衡假设不成立,它可能只是由于月壳结构随深度的变化比模型中假设的更为复杂。因此,需要在以后的工作中对其均衡状态作进一步更有针对性的分析研究,以及其准确合理的滤波范围,即到底哪些频段的水准面高和地形高程对应于月壳内部不同圈层深度结构变化。
5 结 论本文采用GTR技术,利用新的月球重力场模型SGM100h和地形模型STM359_grid-02,同时尽可能剔除表面月海玄武岩填充和深层的异常质量影响,对月壳厚度作了重新研究。GTR技术的一个优点是不需要先验假设参考月壳厚度,避免了由于参考月壳厚度的强制约束带来的系统偏差。经统计分析与比较,与其他技术手段(比如月震数据或者直接的重力反演等)得到的各量有不同程度的符合,表明该方法的可用性。在各月盆则存在着中间较薄,四周逐渐增厚的趋势。这些结果又反过来印证了Airy均衡假说在月球上的适用性。
由于重力场精度和分辨率的限制,还无法精确区分月球内部各圈层的异常密度在表面重力场中所占成分,仅仅将其归因于月壳或粗略的系数截取与滤波所得到的分析结果存在不确定性。模型1中,雨海月壳补偿厚度过大,认为其下部存在高密度物质,仅去除玄武岩填充无法消除其影响,从而推断了它们中心质量瘤的存在主要由月幔抬升引起。即便本文截去了与深层构造相关的低阶项系数,但同时也丢失了部分与均衡补偿有关的信号。同时,限于重力场的精度和分辨率,目前的研究集中在月壳和上月幔,对月核的存在及其物质状态还有待进一步确认,随着GRAIL (Gravity Recovery and Interior Laboratory)计划[29]的实施以及表面地形数据处理的改进[30],对月球重力场和内部从月壳到月核的认识将有一个质的飞跃。
本文所得的平均月壳厚度还可用于进一步计算岩石圈粘性厚度、月球内部应力分析等,综合其他地球物理和地球化学约束,为研究月球演化形成历史提供参考依据。
| [1] | TOKSOZ M,DAINTY A,SOLOMON S,et al.Structure of the Moon[J].Reviews of Geophysics and Space Physics,1974,12:539-567. |
| [2] | NAKAMURA Y,LATHAM G,DORMAN H,et al.Shallow Moonquakes:Depth,Distribution and Implications as to the Present State of the Lunar Interior[C]//Proceedings of Lunar and Planetary Science Conference.New York:Pergamon Press,1979:2299-2309. |
| [3] | KHAN A,MOSEGAARD K,RASMUSSEN K.A New Seismic Velocity Model for the Moon from a Monte Carlo Inversion of the Apollo Lunar Seismic Data[J].Geophysical Research Letter,2000,27(11):1591-1594. |
| [4] | KHAN A,MOSEGAARD K.An Inquiry into the Lunar Interior:a Non-linear Inversion of the Apollo Lunar Seismic Data[J].Journal of Geophysical Research,2002,107(E6):19-44. |
| [5] | LOGNONNE P H,GAGNEPAIN-BEYNEIX J,CHENET H.A New Seismic Model of the Moon:Implication for Structure,Thermal Evolution and Formation of the Moon[J].Earth and Planetary Science Letters,2003,211:27-44. |
| [6] | BRATT S,SOLOMON S,HEAD J.The Evolution of Impact Basins:Cooling,Subsidence,and Thermal Stress[J].Journal of Geophysical Research,1985,90(B14):12415-12433. |
| [7] | ZUBER M,SMITH D,LEMOINE F,et al.The Shape and Internal Structure of the Moon from the Clementine Mission[J].Science,1994,266(5192):1839-1843. |
| [8] | NEUMANN G,ZUBER M,SMITH D,et al.The Lunar Crust:Global Structure and Signature of Major Basins[J].Journal of Geophysical Research,1996,101(E7):16841-16864. |
| [9] | WIECZOREK M,PHILLIPS R.Potential Anomalies on a Sphere:Applications to the Thickness of the Lunar Crust[J].Journal of Geophysical Research,1998,103(E1):1715-1724. |
| [10] | ISHIHARA Y,GOOSSENS S,MATSUMOTO K,et al.Crustal Thickness of the Moon:Implications for Farside Basin Structures[J].Geophysical Research Letter,2009,36:1-4. |
| [11] | POTTS L V.Satellite Geophysical Investigation of the Moon[D].Columbus:Ohio State University,2000. |
| [12] | WIECZOREK M,PHILLIPS R.The Structure and Compensation of the Lunar Highland Crust[J].Journal of Geophysical Research,1997,102(B7):10933-10943. |
| [13] | KONOPLIV A,BINDER A,HOOD L,et al.Improved Gravity Field of the Moon from Lunar Prospector[J].Science,1998,281(5382):1476-1480. |
| [14] | MATSUMOTO K,GOOSSENS S,ISHIHARA Y,et al.An Improved Lunar Gravity Field Model from SELENE and Historical Tracking Data:Revealing the Farside Gravity Features[J].Journal of Geophysical Research,2010,115:1-20. |
| [15] | ARAKI H,TAZAWA S,NODA H,et al.Lunar Global Shape and Polar Topography Derived from Kaguya-LALT Laser Altimetry[J].Science,2009,323(5916):897-900. |
| [16] | SOLOMON S.The Nature of Isostasy on the Moon:How Big a Pratt-fall for Airy Models[C]//Proceedings of Lunar and Planetary Science Conference.New York:Pergamon Press,1978:3499-3511. |
| [17] | HAXBY W,TURCOTTE D.On Isostatic Geoid Anomalies[J].Journal of Geophysical Research,1978,83(B11):5473-5478. |
| [18] | YAN Jianguo,PING Jinsong,MATSUMOTO K,et al.Optimization on Lunar Gravity Field Model Using Chang'E-1 Orbital Tracking Data[J].Scientia Sinica Physica Mechanica&Astronomica,2011,41(7):870-878.(鄢建国,平劲松,Matsumoto K,等.嫦娥一号绕月卫星对月球重力场模型的优化[J].中国科学:物理学力学天文学,2011,41(7):870-878.) |
| [19] | KONOPLIV A,ASMAR S,CARRANZA E,et al.Recent Gravity Models as a Result of the Lunar Prospector Mission[J].Icarus,2001,150(1):1-18. |
| [20] | ARKANI-HAMED J.The Lunar Mascons Revisited[J].Journal of Geophysical Research,1998,103(E2):3709-3739. |
| [21] | MULLER P,SJOGREN W.Mascons:Lunar Mass Concentrations[J].Science,1968,161(3909):680-684. |
| [22] | TURCOTTE D,WILLEMANN R,HAXBY W,et al.Role of Membrane Stresses in the Support of Planetary Topography[J].Journal of Geophysical Research,1981,86(B5):3951-3959. |
| [23] | STEINBERGER B,WERNER S,KOHOUT T.Deep vs.Shallow Origin of Gravity Anomalies and Topography on the Moon[C]//Proceedings of 41st Lunar and Planetary Science Conference.Woodlands:LPI Contribution,2010:1694. |
| [24] | NAMIKI N,IWATA T,MATSUMOTO K,et al.Farside Gravity Field of the Moon from Four-way Doppler Measurements of SELENE (Kaguya)[J].Science,2009,323(5916):900-905. |
| [25] | WIECZOREK M,Jolliff B,Khan A,et al.The Constitution and Structure of the Lunar Interior[J].Reviews in Mineralogy and Geochemistry,2006,60(1):221-364. |
| [26] | CHENET H,LOGNONNE Ph,WIECZOREK M,et al.Lateral Variations of Lunar Crustal Thickness from the Apollo Seismic Data Set[J].Earth and Planetary Science Letters,2006,243:1-14. |
| [27] | RASMUSSEN K,WARREN P.Megaregolith Thickness,Heat Flow and the Bulk Composition of the Moon[J].Nature,1985,313:121-124. |
| [28] | LAMBECK K.Geophysical Geodesy:The Slow Deformations of the Earth[M].Translated by HUANG Liren.Beijing:Surveying and Mapping Press,1995.(库尔特·拉姆贝克.地球物理大地测量学--地球的慢形变[M].黄立人,译.北京:测绘出版社,1995.) |
| [29] | ZUBER M.GRAIL Gravity Mission:Goals and Status[C]//Proceedings of 37th COSPAR Scientific Assembly,Montréal:[s.n.],2008:3658. |
| [30] | ZHAO Shuangmin,LI Deren,MOU Linli.Inconsistency Analysis of CE-1 Stereo Camera Images and Laser Altimeter Data[J].Acta Geodaetica et Cartographica Sinica,2011,40(6):751-755.(赵双明,李德仁,牟伶俐.CE-1立体相机影像与激光高度计数据不一致性分析[J].测绘学报,2011,40(6):751-755.) |