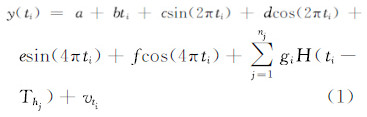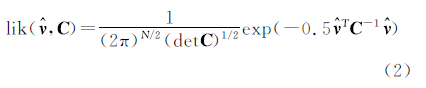2. 武汉大学 卫星导航定位技术研究中心, 湖北 武汉 430079
2. Research Center of GNSS, Wuhan University, Wuhan 430079, China
近20年累积的全球IGS基准站位置时间序列为大地测量学及地球动力学研究提供了宝贵的基础数据。对其进行分析可以获得测站精确的运动趋势,从而更深层次地研究造成测站运动的内部驱动机制,具有重要的理论意义和应用前景。
当前,国内外学者普遍认为GPS位置时间序列噪声特性的最优随机模型为白噪声+闪烁噪声(white noise+ flicker noise,WN+FN)[1,2,3,4,5,6,7, 8]。然而严格来说并非如此,基准站的噪声特性实际较为复杂。例如,文献[9]于2008年估计了加利福尼亚南部及内华达南部地区236个连续GPS运行站的噪声模型,得出50%~60%测站的最佳噪声模型为FN或者随机漫步噪声(random walk noise,RW),25%~30%测站表现为FN+RW,或者非整数谱指数幂律噪声(power law noise,PL),剩余15%测站则位于带通+幂律噪声(band pass+power law noise,BPPL)及一阶高斯马尔科夫+随机漫步噪声(first order Gauss-Markov+random walk noise,FOGMRW)之间。文献[10]分析了香港12个基准站的噪声特性,指出了经主成分空间滤波去除公共误差(common mode error,CME)后的噪声特性可用可变白噪声(variable white noise,VW)加闪烁噪声模型来描述。文献[10,11,12]指出 CGCS框架下我国国家CORS网1999—2009年的坐标时间序列经主成分滤波后的基本特征表现为白噪声、闪烁噪声及随机漫步噪声,且顾及有色噪声的速度误差估值比仅考虑白噪声时大2~6倍。之所以认为FN+WN是代表测站最佳随机特性的噪声模型,分析其原因可能有两方面:① 分析时间序列时并未采用能足够代表基准站噪声特性的较为复杂的随机模型;② 累积的时间序列长度不够,不足以解算噪声的长周期分量。随着时间的推移,GPS基准站坐标时间序列不断增长,噪声的长周期分量(例如谱指数=2的RW噪声)将更加显著,为探测低频噪声的存在提供了有利的条件,因此对GPS时间序列进行更为全面的噪声分析,获取能更准确代表基准站随机特性的噪声模型很有意义。
本文的主要目的在于利用更长的GPS坐标时间序列,采用更多种类的噪声模型组合更可靠地分析中国区域IGS基准站坐标时间序列的随机特征,研究并确定各测站的随机特性是否随着时间序列长度的增加而发生了显著改变,同时计算不同地表质量负载造成的测站位移,给出质量负载改正前后中国区域代表性GPS基准站各分量的最优噪声模型,在此基础上建立噪声模型与地表质量负载及其测站速度、速度不确定度之间的联系。
1 数 据1.1 GPS数据
选取ITRF2005框架下中国区域11个IGS基准站1995—2010年的时间序列①,全面深入分析中国区域IGS基准站的随机特征。各测站的经纬度、测站天线墩类型及时间序列的相关信息见表 1。
① http://igscb.jp1.nasa.gov
| 测 站 | 纬度 /(°) | 经度 /(°) | 时间 段/a | 观测总数/ 跨越年限/a | 阶跃突变 时刻及原因 | 天线墩类型及 地质特征 |
| URUM | 43.807949 | 87.600664 | 1998.8370-2009.5110 | 3904/10.7 | 2008.7199(接收机/天线 变更) | 混凝土天线墩, 基岩 |
| GUAO | 43.471108 | 87.177307 | 2002.4589-2009.5219 | 2582/7.1 | 加固混凝土天线墩, 变质岩 | |
| BJFS | 39.608602 | 115.892483 | 1999.8068—2010.1795 | 3791/10.4 | 混凝土天线墩, 风化沉积岩 | |
| XIAN | 34.368672 | 109.221491 | 1996.3811—2001.4781 | 1872/5.1 | 水泥柱天线墩 | |
| SHAO | 31.099643 | 121.200441 | 1995.0260—2010.1795 | 5552/15.2 | 混凝土天线墩, 沉积岩 | |
| WUHN | 30.531654 | 114.357259 | 1996.0697—2010.1795 | 5155/14.1 | 2002.0616(天线变更),2002.8315(测站记录缺失) | 花岗石天线墩, 沙砾沉积岩 |
| LHAS | 29.657339 | 91.103986 | 1995.3767—2007.0808 | 4303/11.8 | 屋顶水泥柱天线墩, 沙砾层 | |
| KUNM | 25.029540 | 102.797194 | 1998.7712—2010.1795 | 4169/11.4 | 混凝土天线墩, 沉积砾岩 | |
| TWTF | 24.953600 | 121.164500 | 2001.8589—2010.1795 | 3040/8.3 | 屋顶钢筋天线罩 | |
| TCMS | 24.797986 | 120.987389 | 2004.0697—2010.1795 | 2425/6.6 | 屋顶钢筋天线罩,新生沉积粘土 | |
| TNML | 24.797955 | 120.987344 | 2002.4808—2010.1795 | 2813/7.7 | 屋顶钢筋天线罩,新生沉积粘土 |
GPS坐标时间序列呈现显著的季节性变化,通常认为大气压、非潮汐海洋负载及水文负载(这里统称为地表质量负载)是引起测站谐波变化的主要因素[13,14,15,16]。为了从时间序列中分离这些因素的影响,进一步分析其对时间序列噪声特性的影响,本文采用独立的地球物理模型获取不同地表质量负载造成的测站位移。计算大气压负载所需的全球地表气压由美国国家环境预测中心(National Centers for Environmental Prediction,NCEP)再分析数据提供②,时间分辨率为6 h,空间分辨率为2.5°×2.5°;非潮汐海洋负载使用美国国家海洋合作计划(national oceanographic partnership program,NOPP)制定的海洋环流及气候估值(estimating the circulation & climate of the ocean,ECCO)模型提供的全球海底压力格网数据计算③,时间分辨率为12 h,空间分辨率为1°×(0.3°~1.0°)。水文负载考虑积雪深度和土壤湿度引起的地表储水量变化,同样由NCEP再分析数据提供④,空间分辨率为1.875°×1.875°。
②http://www.esrl.noaa.gov/psd/data/gidded/data.ncep.reanalysis.surface.html
③ http://ecco.jpl.nasa.gov/thredds/las/kf080/catalog.html
④ http://www.esrl.noaa.gov/psd/data/gidded/data.ncep.reanalysis.surfaceflux.html
2 数据分析2.1 数据处理策略
就全球GPS单日解时间序列而言,若不采取任何措施减少测站的空间相关噪声,WN+FN是反应N、E、U 3个方向分量噪声特性的最适合随机模型[3]。由于各测站所处的环境不同,产生噪声的来源可能不相同,其噪声特性可能也不完全相同,且现在距文献[3]研究成果已有6年时间,累积的时间序列可能有助于探测低频随机漫步噪声的存在,同时考虑到测站变化的周期性特性,有色噪声的确定性以及GPS技术中可能存在的高斯马尔科夫随机误差,本文选取FN+WN,FN+VW,RW+WN,FN+RW+WN,PL+WN,FOGM+RW+WN以及BPPL+WN共7种噪声模型,采用CATS软件对11个基准站进行噪声分析[17]。采用QOCA⑤对基准站实施包括大气压、非潮汐海洋及水文负载在内的地表质量负载改正,并对改正后的时间序列重新进行噪声分析,以此研究地表质量负载对测站噪声特性的影响。
⑤ http://gipsy.jpl.nasa.gov/qoca
2.2 极大似然估计(maximum likelihood estimation)时间序列噪声分析可以选用频谱分析、MLE等方法完成。频谱分析要求数据均匀采样,且依赖于频谱平均,无法使用时间序列的最长周期数据辅助估计频谱成分。MLE方法可以同时估计噪声类型、周期性振幅、测站速度及不确定度,并且可以避开频谱分析的上述局限性,被认为是目前最准确的噪声分析方法[1],其主要原理是对GPS日解坐标分量时间序列建立如式(1)所示的参数模型
式中,ti为坐标序列日解历元,以年为单位;a为对应于时间序列起始年份第一天的测站位置(即横轴截距);b为线性速度;c、d和e、f分别为年周期项和半年周期项系数,可根据设计方案需要判断是否求解;gj为由于各种原因引起的阶跃式坐标突变,Thj为发生突变的历元;H为海维西特阶梯函数(heaviside step function),发生突变前H值为0,发生突变后H 值为1; vti为观测噪声,可表示成不同噪声模型的组合。若C 表示观测值协方差阵,按照极大似然估计准则可以同时确定a、b、c、d、e、f、gj和噪声分量振幅,即选择不同的噪声模型,确定各噪声分量的大小,使得坐标序列的残差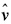 与其协方差的联合概率密度值达到最大
与其协方差的联合概率密度值达到最大
等价于联合概率密度函数值的对数达到最大
2.3 最优噪声模型评价准则根据极大似然估计原理,不同的噪声模型组合将得到不同的极大似然对数值,数值越大,结果越可靠。然而,噪声模型包含的未知参数越多,其MLE值越大[9]。为了确保结果的可靠性,不能简单选择MLE值较大的模型作为最优噪声模型。本文选用Langbein提出的保守估计准则判断不同模型的优劣。首先分别计算FN+WN及RW+WN组合模型的MLE值,选取MLE值较大的模型作为零假设。然后将PL+WN与FN+RW+WN模型的MLE值分别与零假设做比较,如果MLE差值大于2.6则拒绝零假设,认为该模型更优,否则接受零假设,认为所选的复杂模型无效。若PL+WN及FN+RW+WN均优于零假设,则选择MLE值较大者作为“最优”模型。最后将BPPL+WN与FOGM+RW+WN模型计算得到的MLE值与前面得到的“最优”比较,接受BPPL+WN模型的阈值设为2.6,接受FOGM+RW+WN模型的阈值设为5.2[9, 18]。
3 GPS坐标时间序列最优噪声模型的建立3.1 地表质量负载改正前GPS时间序列最优噪声模型的建立
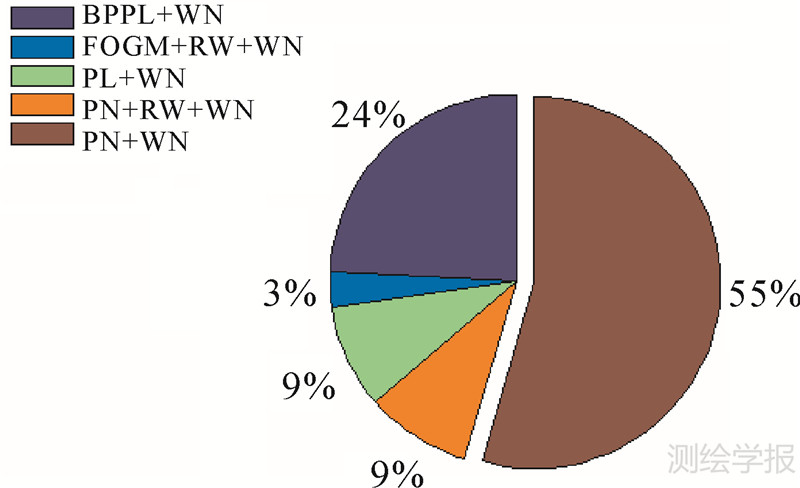
采用2.1节的数据处理策略,根据2.3节的最优噪声模型评价准则,对选取的11个IGS基准站进行上述7种组合噪声模型分析,得到了计算质量负载改正前中国区域IGS基准站分量噪声特性的最优模型。图 1给出了11个IGS站共33个分量的最优噪声模型分布。
|
| 图 1 计算地表质量负载改正前的中国区域IGS基准站分量最优噪声模型分布 Fig. 1Optimal noise model distribution of IGS station components inside China before surface mass loading correction |
从图 1可以看到中国区域IGS基准站分量的噪声特性存在多样性,主要表现为FN+WN和BPPL+WN模型,其他复杂模型也占有一定比例。大部分测站的N、E、U方向的分量表现出不同的噪声特性,因此寻找时间序列变化特征的物理解释时需对各分量区别对待。另外,地理位置相近测站的时间序列也可能具有不同的噪声特 征(例如TNML、TCMS站N方向分量)。考虑到地球物理效应的空间相关性,可能有的测站存在较大的系统误差。
需要注意的是,计算得到的各测站分量FN+VW模型的MLE值明显大于其他组合模型,与袁林果等的结果一致[10],但是VW模型仅能反应测站分量的质量好坏,并不能作为基准站的最优噪声模型。为了确保结果的可靠性,本文最优噪声模型的确定不考虑FN+VW模型。
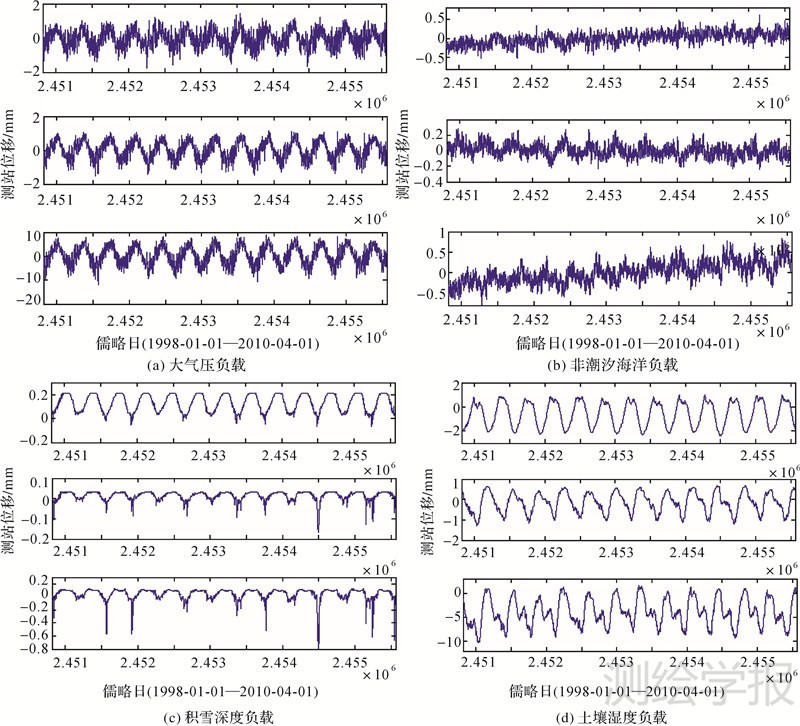
3.2 地表质量负载改正后GPS时间序列最优噪声模型的建立就季节性尺度来说,地表质量负载引起的测站位移是GPS位置时间序列的主要特征[15]。为 了分离地球物理效应的影响,通常采用Farrell格林函数与独立地表质量负载数据的卷积计算不同质量负载引起的测站位移,然后从GPS时间序列里扣除这部分影响[19, 20]。本文采用QOCA根据Farrell格林函数计算了1998-01-01—2010-04-01期间大气压、非潮汐海洋、积雪深度及土壤湿度负载造成的中国区域11个IGS基准站位移。图 2表示4种质量负载造成的SHAO站N、E、U方向 日位移时间序列。从图 2及其他测站计算结果可以看到,不 同地表质量负载对测站的影响均表现为U方向最大,N、E方向影响较小,与已有研究成果一致[7, 10, 18],且造成的测站位移呈现不同的周期特性。部分质量负载对测站的影响与其地理环境密切相关,同一测站对不同质量负载的敏感度也不同。就选取的11个IGS基准站而言,土壤湿度负载造成的测站位移最大,大气压、非潮汐海洋负载次之,积雪负载对测站位移的影响最小,且随纬度降低而减小。
|
| 图 2不同质量负载造成的SHAO站N、E、U方向(上、中、下)位移 Fig. 2 Daily displacement of SHAO in N(top)、E(middle)、U(bottom) directions resulted from different surface mass loadings |
根据上述计算结果对11个IGS基准站进行地表质量负载改正,并对改正后的坐标时间序列重新进行噪声分析,得到了扣除地表质量负载影响后的中国区域IGS基准站分量最优噪声模型。图 3表示各测站分量所属最优噪声模型的比例分布。
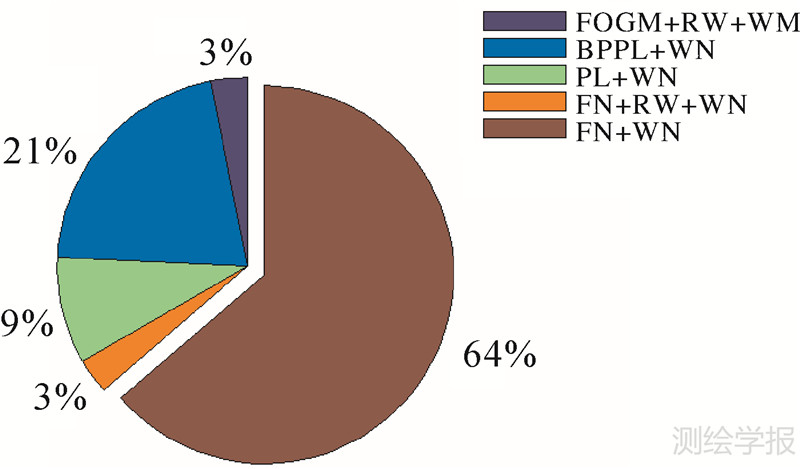 |
| 图 3计算地表质量负载改正后的中国区域IGS基准站分量最优噪声模型分布 Fig. 3Optimal noise model distribution of IGS station components inside China after surface mass loading correction |
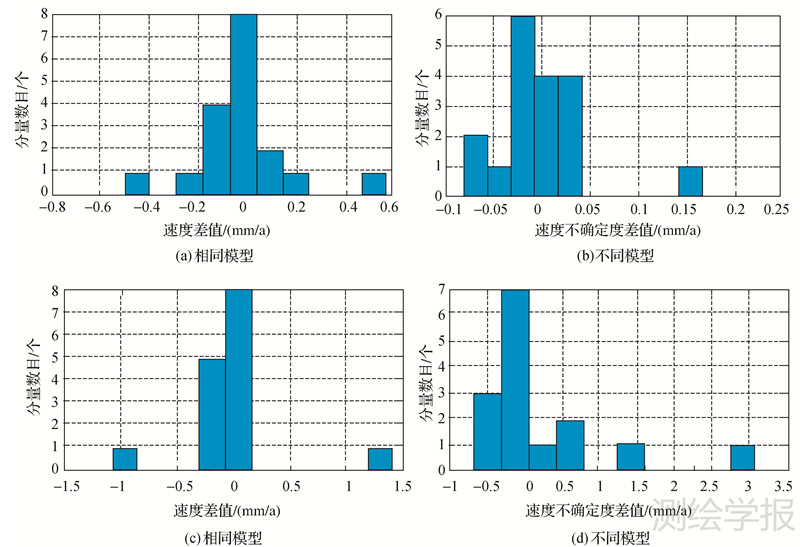
以SOPAC提供的速度及速度不确定度为基准,比较未计算地表质量负载改正前本文确定的测站分量最优噪声模型下的速度及速度不确定度值与SOPAC的差值,相同及不同噪声模型下各测站分量的速度及速度不确定度差值分布图如图 4所示。
从图 4(a)、图 4(b)可以看出,就相同的FN+WN模型而言,本文结果与SOPAC基本一致。83%的速度差值小于0.2 mm/a,N、E方向最大为 0.16 mm/a,个别测站U方向最大达到0.58 mm/a; 78%的速度不确定度差值小于0.04 mm/a,N、E方向最大为0.08 mm/a,个别测站U方向最大为0.17 mm/a。考虑舍入误差的影响,可以认为本文计算得到的结果是合理可靠的。
从图 4(c)、图 4(d)可以看出,相对于FN+WN而言,不同复杂噪声模型对测站速度及不确定度会产生一定的影响,U方向影响最大,E方向次之,N方向最小。其中,40%的测站分量对应于不同噪声模型的速度差值小于0.1 mm/a,47%测站分量的差值约为0.1~0.3 mm/a,13%测站U分量与SOPAC速度差超过1 mm/a;速度不确定度受不同噪声模型的影响较速度大,量级约为亚毫米/年(0.1~0.8 mm/a,占分量总数的87%),少数U分量差值大于1mm/a(占分量总数的13%)。由此可得出结论,对于毫米级高精度参考框架的建立及板块运动分析来说,需顾及不同噪声模型带来的这种差异。由于本文仅采用了11个IGS基准站数据分析测站的噪声特性,仅能反应复杂噪声模型和FN+WN获得的速度及不确定度差异量级,对于不同模型获得的速度不确定度较FN+WN模型的优越性还需采用更多数据进行验证。
|
| 图 4相同及不同噪声模型下测站分量速度及速度不确定度与SOPAC的差值分布 Fig. 4Difference distribution of velocity and velocity uncertainty under the same noise model between our results and SOPAC results together with under different noise models |
表 2列出了地表质量负载改正前后各测站分量的最优噪声模型。
从表 2可以看出,经地表负载改正后11个测站分量的噪声特性发生了变化(占总数的33%),主要体现在N、U方向分量,E方向分量受到的影响较小。噪声类型的变化因站而异,并无显著规律,例如BJFS站的E、U方向分量经负载改正后带通噪声减小,而WUHN站的N、U方向分量的噪声特性却由原来的FN+WN表现为BPPL+WN。由此看来,地表质量负载对测站坐标时间序列的影响不可忽视(尤其是N、U方向分量),为了能对其噪声特性进行准确分析,需要考虑其影响。
经负载改正后FN+WN的比例增大(从51%增大到64%),BPPL+WN和FN+RW+WN比例减少,各测站分量的BP(周期为0.5~1.5a)及RW振幅普遍出现变化。比较3.2得到的负载改正结果,可以认为计算的4种地表质量负载会引起除周年、半周年以外的谐波变化,对测站时间序列的影响可能表现为BP或者RW特性。考虑到负载模型的准确性以及采用测站数目的局限性,关于其确定影响还需要做进一步深入的研究。
| 测站名 | N方向分量最优噪声模型 | E方向分量最优噪声模型 | U方向分量最优噪声模型 | |||
| 计算质量 负载改正 | 未计算质量 负载改正 | 计算质量 负载改正 | 未计算质量 负载改正 | 计算质量 负载改正 | 未计算质量 负载改正 | |
| URUM | FN+WN | PL+WN | FOGM+RW+WN | FOGM+RW+WN | PL+WN | FN+RW |
| GUAO | PL+WN | BPPL+WN | BPPL+WN | BPPL+WN | BPPL+WN | BPPL+WN |
| BJFS | FN+WN | FN+WN | FN+WN | BPPL+WN | FN+WN | BPPL+WN |
| XIAN | FN+WN | FN+WN | BPPL+WN | FN+WN | FN+WN | FN+WN |
| SHAO | FN+WN | FN+WN | BPPL+WN | BPPL+WN | FN+WN | FN+WN |
| WUHN | BPPL+WN | FN+WN | FN+WN | FN+WN | BPPL+WN | FN+WN |
| LHAS | FN+WN | FN+WN | FN+WN | FN+WN | FN+WN | FN+WN |
| KUNM | FN+WN | FN+WN | BPPL+WN | BPPL+WN | FN+WN | FN+WN |
| TWTF | FN+WN | FN+RW | FN+WN | FN+WN | FN+RW | FN+RW |
| TCMS | FN+WN | BPPL+WN | FN+WN | FN+WN | FN+WN | FN+WN |
| TNML | PL+WN | PL+WN | FN+WN | FN+WN | FN+WN | FN+WN |
| 注:黑体部分表示计算地表负载改正后最优噪声模型发生变化的测站分量 | ||||||
本文确定了中国区域IGS基准站的最优噪声模型,计算了包括大气压、非潮汐海洋、土壤湿度和积雪深度负载在内的地表质量负载对坐标时间序列的影响,得出以下结论:
(1)国区域IGS基准站坐标时间序列的噪声模型存在多样性,且N、E、U方向分量表现出不同的噪声特性。未计算地表质量负载改正前,3%测站分量的最优噪声模型表现为FOGM+RW+WN,PL+WN、FN+RW+WN 模型各占9%,BPPL+WN 模型占24%,剩余55%的测站分量采用FN+WN模型描述最为合适。
(2) 对于FN+WN模型而言,不同复杂噪声模型对测站速度的影响约为0.01~0.3 mm/a,但少数测站U分量超过1 mm/a。速度不确定度受噪声模型的影响较大,量级约为亚毫米/年(0.1~ 0.8 mm/a),建立毫米级参考框架及板块运动分析时需顾及这种差异。采用中国区域IGS基准站数据仅能初步反应复杂噪声模型和FN+WN模型获得的速度及速度不确定度的差异量级,对于不同模型获得的速度不确定度的优越性(即哪种模型获得的不确定度更接近测站的实际状况)还需要更多测站数据进行验证。
(3)表质量负载会造成测站的噪声特性变化,主要体现在N、U方向分量,E方向分量受到的影响较小,且噪声类型的变化因站而异,并无显著规律。计算负载改正后,FN+WN模型的比例增大(64%),FOGM+RW+WN、FN+RW模型各占测站分量总数的3%,PL+WN模型占9%,21%的测站分量噪声特性采用BPPL+WN模型描述最为合适。
致谢:感谢SOPAC提供的IGS基准站坐标时间序列;S.D.P.Williams博士提供的CATS软件及在本文确定IGS基准站分量最优噪声模型过程中给予的建议和帮助;董大南博士提供的QOCA软件;计算大气压、土壤湿度和积雪深度负载改正采用的全球地表气压及地表储水量变化数据由美国国家环境预测中心NCEP提供;计算非潮汐海洋负载采用的全球海底压力格网数据由美国国家海洋合作计划NOPP提供。
| [1] | ZHANG J, BOCK Y, JOHNSON H, et al. Southern California Permanent GPS Geodetic Array: Error Analysis of Daily Position Estimates and Site Velocities[J]. Journal of Geophysical Research, 1997,102 (B8):18035-18055. |
| [2] | WILLIAMS S D P. The Effect of Coloured Noise on the Uncertainties of Rates Estimated from Geodetic Time Series[J]. Journal of Geodesy, 2003, 76(9-10): 483-494. |
| [3] | WILLIAMS S D P, BOCK Y, FANG P, et al. Error Analysis of Continuous GPS Position Time Series[J]. Journal of Geophysical Research, 2004, 109(B3): 1-19. |
| [4] | MAO A, HARRISON C G A, DIXON T H. Noise in GPS Coordinate Time Series[J]. Journal of Geophysical Research, 1999, 104(B2): 2797-2816. |
| [5] | QIAO Xuejun,WANG Qi,WU Yun,et al. Time Series Characteristic of GPS Fiducial Stations in China[J]. Geomatics and Information Science of Wuhan University, 2003, 28(4): 413-416. (乔学军,王琪,吴云,等. 中国大陆GPS基准站的时间序列特征[J]. 武汉大学学报: 信息科学版, 2003, 28(4): 413-416.) |
| [6] | HUANG Liren. Noise Properties in Time Series of Coordinate Component at GPS Fiducial Stations[J]. Journal of Geodesy and Geomatics, 2006, 26(2): 31-38. (黄立人. GPS基准站坐标分量时间序列的噪声特性分析[J]. 大地测量与地球动力学, 2006, 26(2): 31-38.) |
| [7] | ZHU Wenyao, FU Yang, LI Yan. Global Height Vibration and its Seasonal Variation Induced by GPS Height[J]. Science in China: Series D, 2003, 33(5): 470-481. (朱文耀,符养,李彦. GPS高程导出的全球高程振荡运动及季节性变化[J]. 中国科学: D辑, 2003, 33(5): 470-481.) |
| [8] | HAN Ying, FU Yang. Analysis of GPS Time Series of Height Component[J]. Geomatics and Information Science of Wuhan University, 2003, 28(4): 425-428. (韩英,符养. GPS高程数据时间序列分析[J]. 武汉大学学报: 信息科学版, 2003, 28(4): 425-428.) |
| [9] | LANGBEIN J. Noise in GPS Displacement Measurements from Southern California and Southern Nevada[J]. Journal of Geophysical Research, 2008, 113(B5): 1-12. |
| [10] | YUAN Linguo, DING Xiaoli, CHEN Wu, et al. Characteristics of Daily Position Time Series from Hong Kong GPS Fiducial Network[J]. Chinese Journal of Geophysics, 2008, 51(5):1372-1384. (袁林果,丁晓利,陈武,等.香港GPS基准站坐标序列特征分析[J].地球物理学报,2008,51(5):1372-1384.) |
| [11] | JIANG Zhihao, ZHANG Peng, BI Jinzhong, et al. The Model of Crustal Horizontal Movement Based on CGCS2000 Frame[J]. Acta Geodaetica et Cartographica Sinica, 2009, 38(6): 471-476. (蒋志浩,张鹏,秘金钟,等. 基于CGCS2000的中国地壳水平运动速度场模型研究[J]. 测绘学报, 2009, 38(6): 471-476.) |
| [12] | JIANG Zhihao, ZHANG Peng, BI Jinzhong, et al. Velocity Estimation on the Colored Noise Properties of CORS Network in China Based on the CGCS2000 Frame[J]. Acta Geodaetica et Cartographica Sinica, 2010, 39(4): 355-363. (蒋志浩,张鹏,秘金钟,等. 顾及有色噪声影响的CGCS2000下我国CORS站速度估计[J]. 测绘学报, 2010, 39(4): 355-363.) |
| [13] | JIANG Weiping, LI Zhao, LIU Wanke, et al. Some Thoughts on Establishment and Maintenance of Terrestrial Reference Frame Considering Non-linear Variation[J]. Geomatics and Information Science of Wuhan University, 2010, 35(6): 665-669. (姜卫平,李昭,刘万科, 等. 顾及非线性变化的地球参考框架建立与维持的思考[J]. 武汉大学学报: 信息科学版, 2010, 35(6): 665-669.) |
| [14] | TIAN Yunfeng, SHEN Zhengkang. Progress on Reduction of Non-tectonic Noise in GPS Position Time Series[J]. Acta Seismologica Sinica, 2009, 31(1): 68-81. (田云锋,沈正康. GPS坐标时间序列中非构造噪声的剔除方法研究进展[J]. 地震学报, 2009, 31(1): 68-81.) |
| [15] | DONG D, FANG P, BOCK Y, et al. Anatomy of Apparent Seasonal Variations from GPS-derived Site Position Time Series[J]. Journal of Geophysical Research, 2002, 107(B4): 1-17. |
| [16] | WANG Min, SHEN Zhengkang, DONG Danan. Effects of Non-tectonic Crustal Deformation on Continuous GPS Position Time Series and Correction to Them[J]. Chinese Journal of Geophysics, 2005, 48(5): 1045-1052. (王敏,沈正康,董大南.非构造形变对GPS连续站位置时间序列的影响和修正[J]. 地球物理学报, 2005, 48(5): 1045-1052.) |
| [17] | WILLIAMS S D P. CATS: GPS Coordinate Time Series Analysis Software[J]. GPS Solution, 2008, 12(2): 147-153. |
| [18] | LANGBEIN J. Noise in Two-color Electronic Distance Meter Measurements Revisited[J]. Journal of Geophysical Research, 2004, 109( B4): 1-16. |
| [19] | FARRELL W E. Deformation of the Earth by Surface Loads[J]. Reviews of Geophysics and Space Physics, 1972, 10(3): 761-797. |
| [20] | TREGONING P, DAM T V. Effects of Atmospheric Pressure Loading and Seven-parameter Transformation on Estimates of Geocenter Motion and Station Heights from Space Geodetic Observations[J]. Journal of Geophysical Research, 2005, 110(B03): 1-12. |