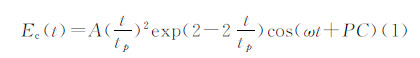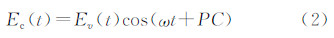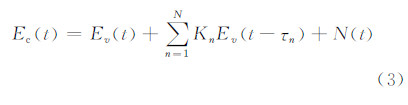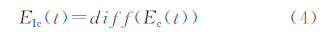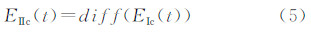2. 中国科学院 研究生院，北京100049；
3. 海军工程大学 导航工程系，湖北 武汉430033
2. Graduate University of Chinese Academy of Sciences, Beijing 100049, China;
3. Department of Navigation, Naval University of Engineering, Wuhan 430033, China
1 引 言
罗兰C系统是一个工作频率为100kHz的陆基双曲线无线电导航系统。罗兰C系统信号通过地波和天波两种路径传播至接收点，使得实际接收的罗兰C信号为天波与地波的合成波[1]。但由于电离层随着时间、季节、气候变化剧烈的特性，容易造成天波信号产生畸变，致使接收点的合成信号十分不稳定，影响最终的定位结果[2]。因此，文献[3]提出利用天地波识别技术的思路，依据识别的天波延迟时间选择天波到达之前最近的采样基准点，以获取最高的信噪比。因此，如何准确、有效地估计罗兰C信号天波相对地波的延迟时间是提高接收设备定位速率、定位精度和可靠性的最关键技术之一[1]。
目前，文献[12]进行了多径条件下高分辨率的时间延迟估计研究，通过文献[3] 对罗兰C信号天波延迟的覆盖范围研究得出了天波延迟的数学表达式，并提出了采用频谱相除法得到天波延迟的数学模型，形成了罗兰C信号天波延迟估计的重要理论基础，在此基础上，形成了经典的Fourier反变换法——IFFT和将频域功率谱转换到时域中的功率谱分析法。文献[4, 5, 6]研究了利用IFFT方法估计天波延迟时间，对其主要性能指标(如信噪比、窗口宽度、波天波强度比)进行了评估。由于接收机带宽有限和提高信噪比的要求，所得数据要加窗处理，加窗会影响信号的形状和分辨率。IFFT算法由于加窗后可用数据被截短致使分辨率较低，在噪声干扰严重的地方要求时延值不能太小。因此，这种方法的实际应用价值不高。文献[7, 8]采用平稳随机信号的ARMA模型算法；文献[9, 10]利用AR模型进行建模；文献[11, 12, 13, 14, 15]采用特征矢量分解法进行目标信号检测；文献[16, 17]提出了ESPRIT算法进行研究分析。这些方法都是基于信号频域和功率谱分析的理论，通过估计相关矩阵延长可用数据长度，来减少数据截短对分辨率的影响，因此，具有较高的时间分辨率。同时，文献[18]对IFFT法、ARMA和MUSIC等方法对罗兰C信号天地波延迟估计的准确度和分辨率进行了仿真比较分析。在实际应用中，当罗兰C信号接收信噪比较低的情况下，以上方法均易出现峰值不明显而形成多个峰值无法完成自动识别的问题。本文采取提取的罗兰C信号包络，并利用其相关特性的方式，提出了基于罗兰C信号优化包络相关系数的时域分析法，很好地解决了上述问题。
2 罗兰C信号改进 2.1 标准罗兰C信号根据美国海岸警卫队发布的单个罗兰C发射信号的格式，标准罗兰C信号如图 1所示，其数学表达式Ec(t)为
式中，A是信号脉冲的最大幅度；t表示信号传播时间；tp是脉冲上升沿的时间(官方选用65 μs)；ω表示角频率即200 000π rad/s；PC表示相位编码，通常取0或π。标准罗兰C信号实际包含包络和载频两部分信号，包络信号如图 2所示。假设包络函数项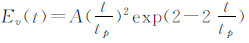
，则将式(1)简写为式(2)
|
| 图 1 标准罗兰C射频信号 Fig. 1 Standard Loran C radio-frequency signal |
载频项可以通过模拟的包络检波电路或者数字的包络提取方法进行消除，得到包络函数项Ev(t)，再依据文献[19]的罗兰C信号数学模型可得地波信号加上天波信号以及噪声和干扰信号的实际罗兰信号包络数学模型
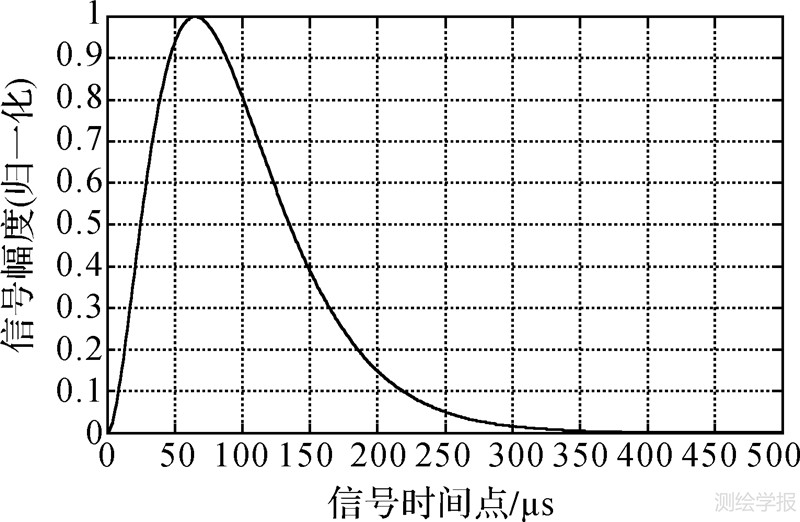
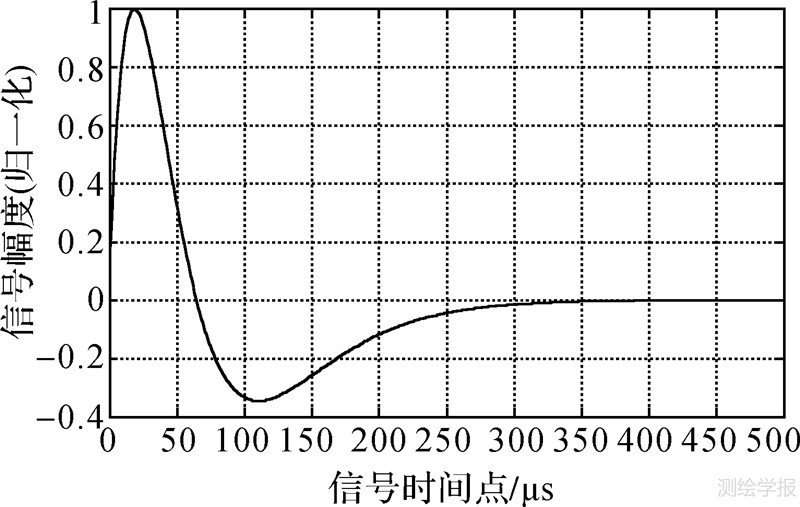
2.2 罗兰C信号优化
根据图 2，罗兰C信号包络的上升沿时间为65 μs，上升时间较短。但是，由于天波的延迟为37.5~1500 μs，最小的延迟小于信号包络上升沿，在进行时域相关时，会影响相关的结果，因此，必须通过缩短信号上升沿时间的方式，以保证相关结果的可用性。所以，利用式(4)的一次微分法和式(5)的二次微分法将罗兰C信号包络进行变形，变换后的罗兰C信号如图 3和图 4所示。
|
| 图 2 标准罗兰C包络信号 Fig. 2 Standard Loran C envelope signal |
|
| 图 3 罗兰C包络信号的一次微分 Fig. 3 Differential of Loran C envelope signal |
|
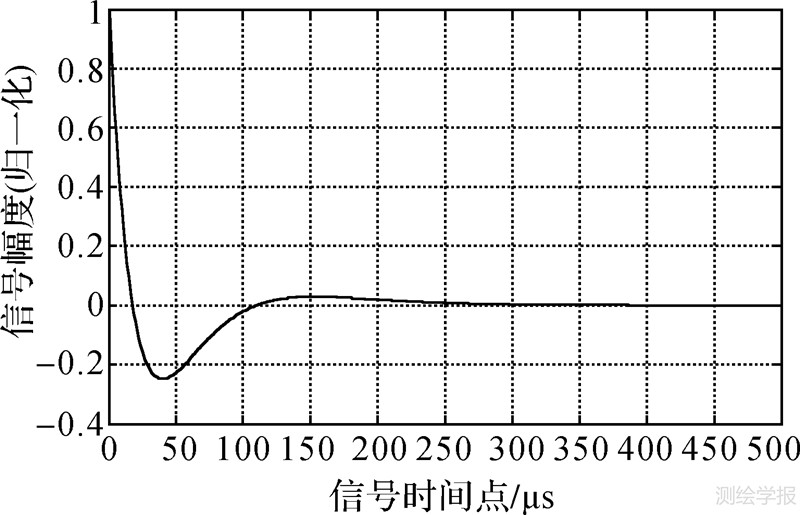
| 图 4 罗兰C包络信号的二次微分 Fig. 4 Quadratic differential of Loran C envelope signal |
由图 3、4可以明显看出，一次微分变换后信号的上升沿时间缩短为19 μs，最小的天波延迟相当于信号包络上升沿的2倍，二次微分变换后信号的峰值出现在1 μs上，上升沿变得十分陡峭，信号的相关结果的可用性将随之提高。下面通过仿真试验和实际信号测试来验证该方法是否满足罗兰C天地波信号延迟估计的需求。
3 相关系数匹配法相关系数匹配法是一种经典的匹配滤波技术，是指通过计算参考信号和被测信号的互相关系数来判别2个信号参数之间相似关系的过程，该相似程度可体现信号的形状和时序之间的关系[19]。根据数学上的定义，假设接收信号f1(t)和参考信号f2(t)满足下列关系
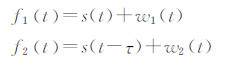
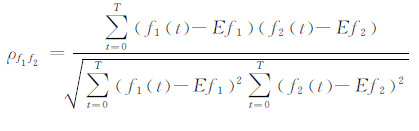
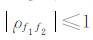，在[-1,1]绝对尺度范围之间衡量两者的相似性。通常情况下，ρf1f2越接近1，两者越近似的有线性关系 [20]。因此，该方法又被称为归一化相关系数法，且具有下几个特点[19]：
(1) 其相关系数值的分布具有区域性，即在某些区域会出现相关峰。其中有1个特别突出的相关峰，这个峰的峰值比其他相关峰的峰值大，这个峰所在的位置就是最后的匹配点位置。
(2) 相关峰有正相关峰和负相关峰。
(3) 绝大部分的相关系数值都比较小。
这种匹配滤波技术被认为是最优和最有效的时延估计方法，能够得到最大输出信噪比，并且与输入信号的波形以及加性噪声的分布特性无关[22]。因此，可以利用这些特性进行罗兰 C 天地波信号延迟的估计。
4 包络相关法仿真与试验 4.1 包络相关法仿真为检验上述方法评估罗兰C信号天地波延迟性能的效果，利用MATLAB构造一个接收点处的罗兰C信号。根据罗兰C的数学模型，信号由地波、天波和干扰噪声组成，地波信号在100 μs处产生，天波信号延迟地波由60 μs，且相对地波信号强度为0 dB，同时加载服从正态分布的白噪声，其信噪比在接收机天线端为-10 dB(满足美国海岸警卫队定义的最小罗兰C接收性能标准)。
如图 5所示，具体实现步骤如下：
|
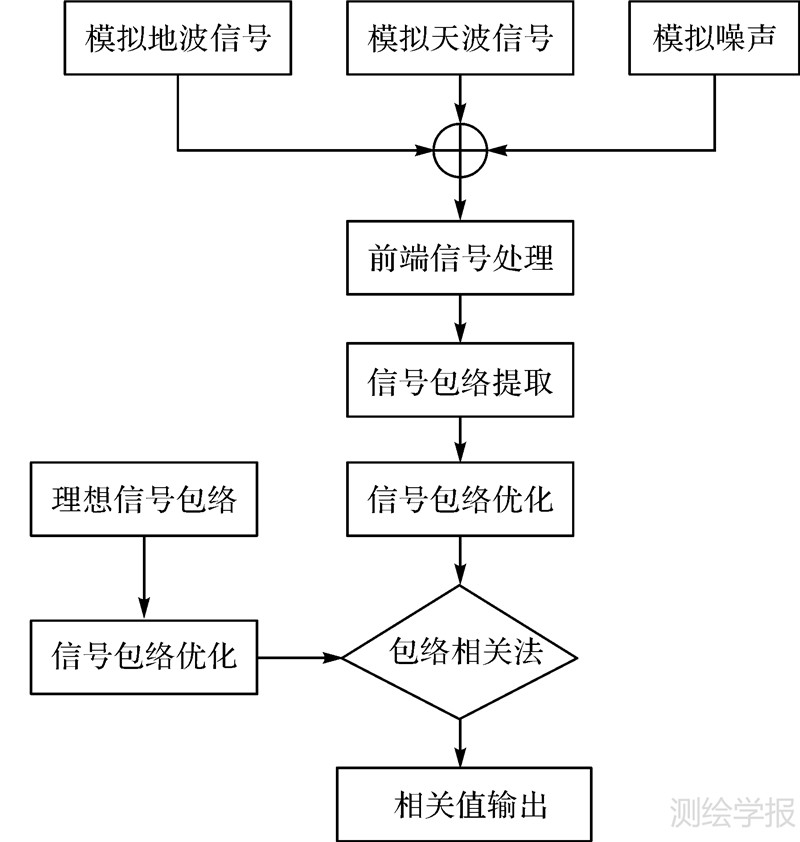
| 图 5 优化包络相关算法流程图 Fig. 5 Optimization envelope correlation algorithm flow diagram |
(1) 产生模拟混合信号；
(2) 利用高阶的FRI数字带通滤波器对前端信号进行滤波和自适应限波处理；
(3) 利用小波变换法或希尔伯特变换进行罗兰C信号包络提取，输出天地波信号包络及带内噪声；
(4) 本地产生的理想罗兰C信号包络与经过处理后提取的被检测信号包络分别进行一次微分和二次微分；
(5) 利用归一化相关系数法进行包络相关处理；
(6) 根据相关后的峰值估计出天地波信号的时间延迟值。
按照仿真步骤，分别利用经典的加窗IFFT方法和上述介绍的方法进行仿真，其结果如图 6~图 8所示，分析如下：
(1) 图 6为利用经典的加窗IFFT方法将模拟的接收点罗兰C合成信号进行模拟仿真结果。从图中可以看出，除了在100 μs和160 μs处有两个尖峰以外，还可以看到多处有峰值的存在。主要原因是合成信号受到噪声干扰的影响，因此，无法准确地进行时间延迟估计。
|
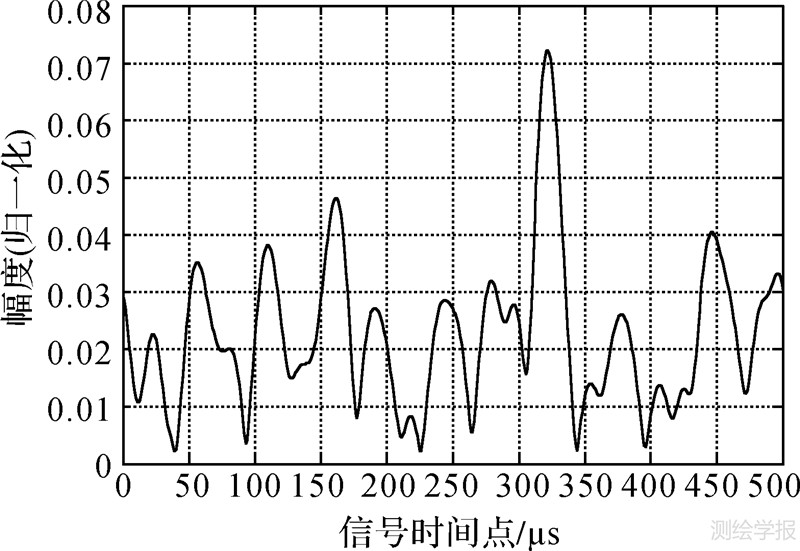
| 图 6 基于加窗IFFT的天波延迟估计 Fig. 6 Skywave delay estimate based on window IFFT |
(2) 图 7为利用二次微分优化相关方法将模拟的接收点罗兰C合成信号进行模拟仿真。图中可较为清晰地看出在100 μs和160 μs处有两个明显的尖峰，但尖峰处有毛刺，使尖峰识别的准确率降低。主要原因也是由于合成信号受到噪声干扰，若噪声强度增强则无法进行识别。
|
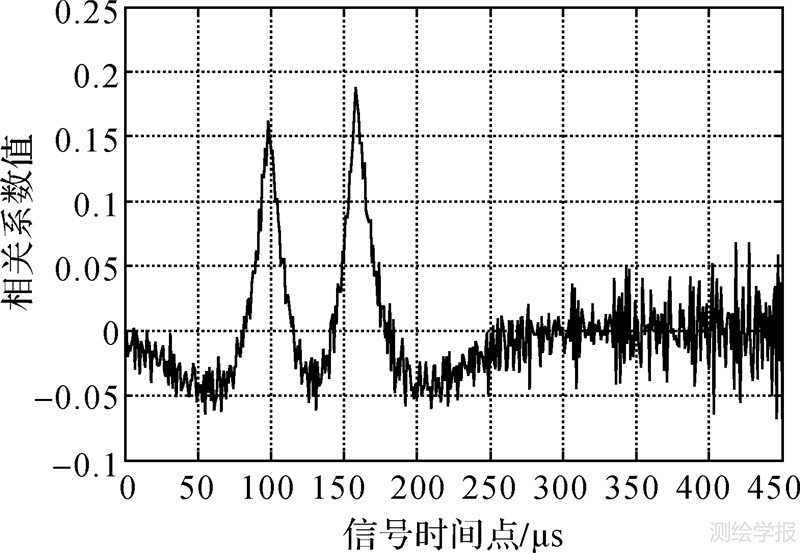
| 图 7 基于二次微分包络相关的天波延迟估计 Fig. 7 Skywave delay estimate based on Quadratic differential |
(3) 图 8为利用一次微分优化相关方法将模拟的接收点罗兰C合成信号进行模拟仿真，从图中可见在100 μs和160 μs处有两个的峰值，而且峰值区域没有明显的毛刺干扰，识别的准确率较高，相对前两种方法有明显的抗干扰能力。但是，也发现相对前2种方法，该方法的识别分辨率较低。
|
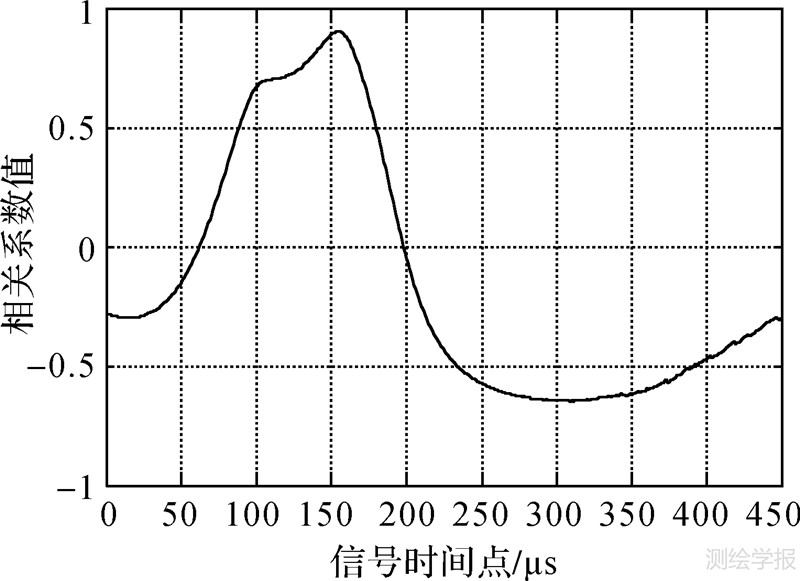
| 图 8 基于一次微分包络相关的天波延迟估计 Fig. 8 Skywave delay estimate based on differential |
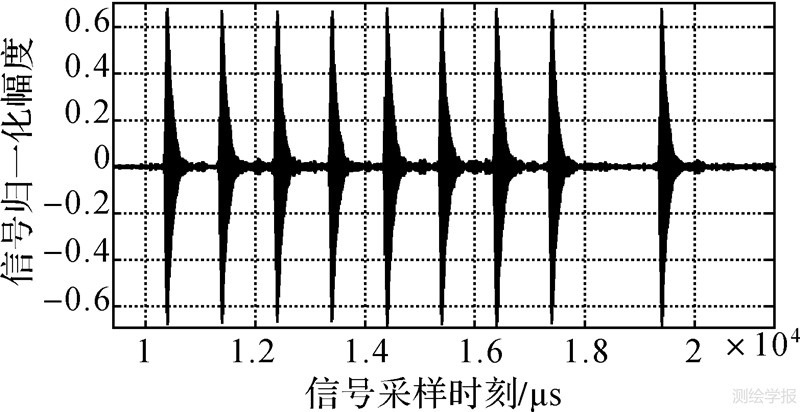
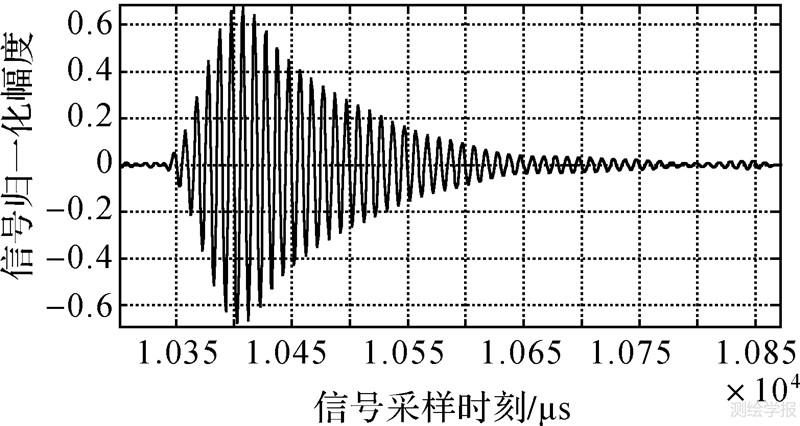
为了进一步验证算法的实际应用效果，利用一次微分包络相关技术对罗兰C 信号的天波延迟进行了实际测试。2011-05-20,15:00，晴天天气，选择武汉一处空旷的场地，接收由安徽宣城导航台作为主台发射的罗兰C信号进行实测。在这种环境条件下天波变化相对平稳，测试结果稳定，易于验证测试方法的正确性。如图 9、图 10所示，分别为实测的罗兰C主台脉冲群和单个的实测罗兰C信号；分别利用一次微分优化包络相关技术和IFFT算计进行识别，如图 11、图 12所示；再选取10 300 μs至1 108 001 μs之间的100个罗兰C信号进行统计测试验证，如图 13所示。
|
| 图 9 实测的罗兰C主台脉冲群 Fig. 9 Measured Loran C master station pulse group |
|
| 图 10 单个实测罗兰C信号 Fig. 10 Single measured Loran C signal |
|
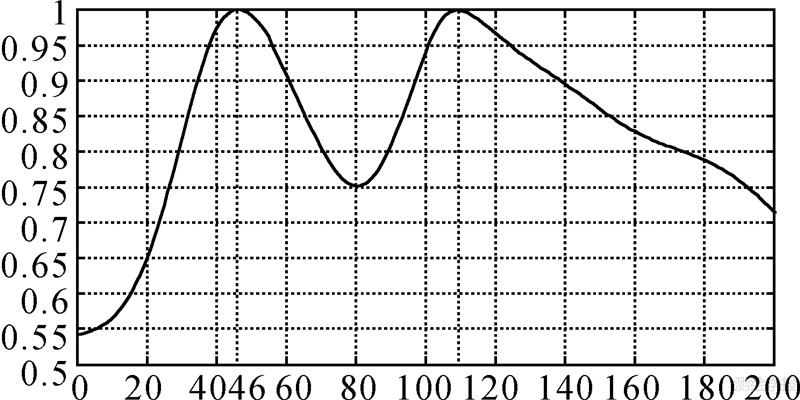
| 图 11 基于一次微分包络相关的实测信号估计 Fig. 11 Measured signal estimate based on differential |
|
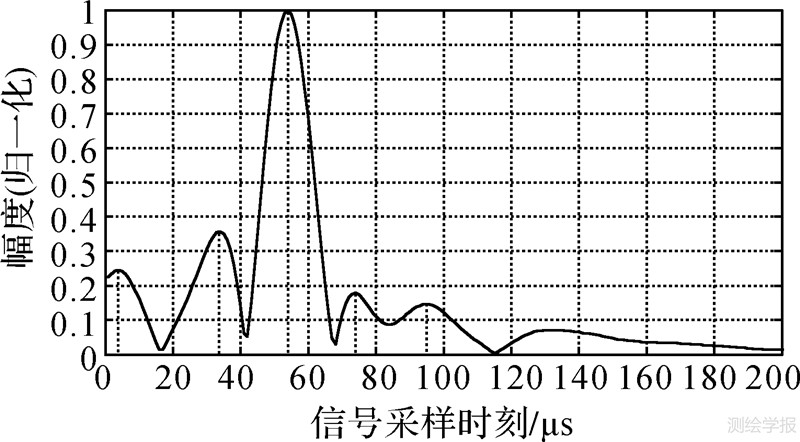
| 图 12 基于IFFT法的实测信号估计 Fig. 12 Measured signal estimate based on window IFFT |
|
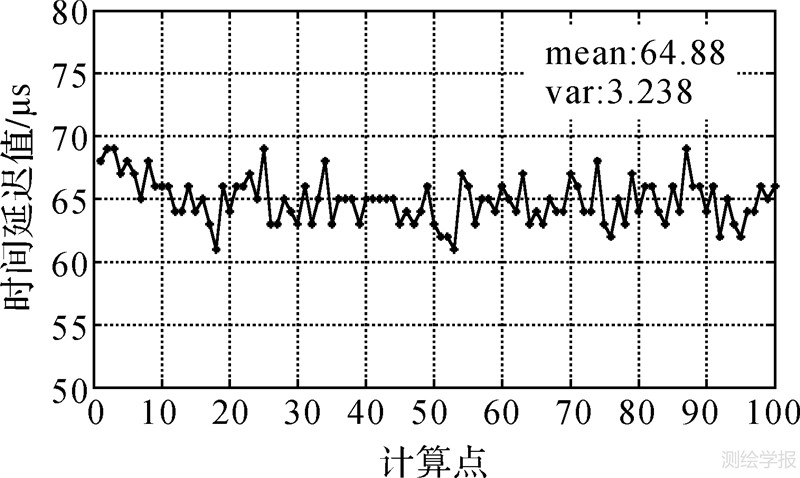
| 图 13 100个罗兰C主台实测信号天波延迟估计统计图 Fig. 13 100 Loran C master station measured signals estimate cartogram |
通过上述试验验证，可得如下结论：
(1) 如图 11所示，利用一次微分优化包络相关技术进行测试，可在46 μs和109 μs处清晰地的得到两个相关峰值，恰好对应地波信号和天波信号到达的时刻，可估算出两个峰值间的间隔，即天地波信号的延迟为63 μs。
(2) 如图 12所示，经典的IFFT法进行实际信号处理中在4 μs、34 μs、54 μs、74 μs等多处产生脉冲峰值，已不能清晰、准确地对峰值的具体性质作出判断，无法对天波信号的延迟进行估计。
(3) 如图 13所示，经过100个实测罗兰C信号的时间延迟估计值的统计可知，其均值为64.88 μs，方差为3.238 μs，方差值小于信号载频周期的二分之一，因此，所得的结果不仅可以用于天波延迟的估计，还可以作为判别相位跟踪和周期识别正确率的辅助依据[1]。
5 结 论通过以上的仿真和试验验证可知，利用优化包络相关法可以很好地解决较低信噪比条件下，实际信号接收时出现的峰值不明显和多个峰值无法自动识别的问题。该方法具有较好的评估准确性和抗噪能力，极大地改善了峰值的识别能力，能满足现代数字化罗兰C接收机应用的实际需求。同时，为了解决罗兰C信号交叉干扰信号影响的问题，通常不使用单个信号进行分析，而是采用信号积累的方式对10个或者20个周期的信号进行累加，利用合成的信号进行时间延迟的估计，以消除交叉干扰对信号的影响。通过分析也发现，利用优化包络相关法存在分辨率不高的问题，亟待后期的研究分析和解决。
| [1] | WU Miao, ZHU Tao, LI Fangneng, et al. Principal and Application of Radio Navigation[M]. Beijing: National Defence Industry Press, 2008: 170-182. (吴苗, 朱涛, 李方能, 等. 无线电导航原理及应用[M]. 北京: 国防工业出版社, 2008: 170-182.) |
| [2] | YUAN Yunbin, OU Jikun. The Effects of Instrumental Bias in GPS Observations on Determining Ionospheric Delays and the Methods of Its Calibration[J]. Acta Geodaetica et Cartographic Sinica, 1999, 28(2): 110-114. (袁运斌,欧吉坤. GPS观测数据中的仪器偏差对确定电离层延迟的影响及处理方法[J]. 测绘学报, 1999, 28(2): 110-114.) |
| [3] | LAST J D, FARNWORTH R G, SEARLE M D. Effect of Skywave Interference on the Coverage of Loran-C[J]. IEE Proceedings-F: Radar and Signal Processing, 1992, 139(4): 306-314. |
| [4] | MOHAMMED A F. Effect of Loran-C Signal Parameters on Skywave Delay Estimation of IFFT Technique[J]. Electronics Letters, 2003, 39(14): 1091-1092. |
| [5] | MOHAMMED A F, LAST J D. IFFT Technique for Skywave Detection in Loran-C Receivers[J]. Electronics Letters, 2001, 37(6): 398-400. |
| [6] | ZHU Yinbing, XU Jiangning, WANG Hongxing, et al. New Loran C Sky-wave and Ground-wave Identification Algorithm Based on IFFT Spectral Division[J]. Journal of Electronics & Information Technology, 2009, 31(5): 1153-1156. (朱银兵, 许江宁, 王红星, 等. 基于IFFT频谱相除的罗兰C天地波识别新算法[J]. 电子与信息学报, 2009, 31(5): 1153-1156.) |
| [7] | MOHAMMED A F, LAST J D. Loran-C Skywave Detection Using Rational Modeling Techniques[C]//6th International Conference on Radio Receivers and Associated Systems. Bath: IEEE,1995: 100-104. |
| [8] | MOHAMMED A F, LAST J D. Loran-C Skywave Delay Detection Using ARMA Algorithm [J]. Electronics Letters,1998,34(17):1654-1655. |
| [9] | MOHAMMED A F, LAST J D. Loran-C Skywave Delay Estimation Using the AR Algorithm[J]. Electronics Letters, 1998, 34(23): 2217-2219. |
| [10] | WU Fumei, YANG Yuanxi. Gyroscope Random Drift Model Based on the Higher-order AR Mode[J]. Acta Geodaetica et Cartographic Sinica, 2007, 36(4): 389-394. (吴富梅,杨元喜. 基于高阶AR模型的陀螺随机漂移模型[J]. 测绘学报, 2007, 36(4): 389-394.) |
| [11] | YI Bian. Eigen-decomposition Techniques for Loran-C Skywave Estimation[J]. IEEE Transactions on Aerospace and Electronics Systems, 1997, 33(1): 117-125. |
| [12] | YI B, LAST J D. Loran-C Skywave Estimation Using Eigen-decomposition Techniques[J]. Electronics Letters,1995,31(2):133-134. |
| [13] | MOHAMMED A F, LAST J D. High Resolution Techniques for Loran-C Skywave Delay Estimation[J]. Electronics Letters,1999,35(18):1516-1517. |
| [14] | HU Dongliang,YANG Yingchun,FAN Juhong. Loran-C receiver Sky-wave Detection Based on MUSIC Algorithms[J]. Journal of Naval University of Engineering,2006,18(3): 7-9.(胡东亮,杨迎春,范菊红. 基于MUSIC算法的罗兰C接收机天地波自动识别方法研究[J]. 海军工程大学学报,2006,18(3):7-9.) |
| [15] | HUAN Ruohong,YANG Ruliang. A Target Detection Method for SAR Image Based on Feature Classification Discrimination[J]. Acta Geodaetica et Cartographic Sinica,2009,38(4):324-329.(宦若虹,杨汝良. 一种基于特征分类辨识的SAR图像目标检测方法 [J]. 测绘学报,2009,38(4):324-329.) |
| [16] | ROY R,KAILATH T. ESPRIT—Estimation of Signal Parameters via Rotational Invariance Techniques[J]. IEEE Transactions on Acoustics, Speech and Signal Processing,1989,37(7):984-995. |
| [17] | TAN Lulu,YANG Libo,YANG Ruliang. Investigation of Tree Height Retrieval with Polarimetric SAR Interferometry Based on ESPRIT Algorithm[J]. Acta Geodaetica et Cartographic Sinica,2011,40(3):296-300. (谈璐璐,杨立波,杨汝良. 基于ESPRIT算法的极化干涉SAR植被高度反演研究[J]. 测绘学报,2011,40(3):296-300.) |
| [18] | WU Miao, XU Jiangning, CHEN Zhiyong, et al. Skywave Delay Estimation of Loran C Based on Modern Signal Processing Methods[J]. Hydrographic Surveying and Charting,2011,31(2):49-51.(吴苗,许江宁, 陈志勇,等. 基于现代信号处理的罗兰C天波延迟估计研究[J]. 海洋测绘,2011,31(2):49-51.) |
| [19] | ZHU Yongsong,GUO Chengming. The Research of Correlation Matching Algorithm Based on Correlation Coefficient[J]. Signal Processing,2003,19(6):531-534.(朱永松,国澄明. 基于相关系数的相关匹配算法的研究[J]. 信号处理,2003,19(6):531-534.) |
| [20] | WEI Jihua,FU Sihua. Real-time Matching Algorithm Based on the Property of Correlation Coefficients[J]. Optical Technique,2008,34(sup):100-102.(魏继华,伏思华. 基于相关系数特性的实时匹配算法[J]. 光学技术,2008,34(增刊):100-102.) |
| [21] | LI Xuemei,TAO Ran,WANG Yue. Summary of the Time Delay Estimation[J]. Radar Science and Technology,2010,8(4):362-371. (李雪梅,陶然,王越. 时延估计技术研究[J]. 雷达科学与技术,2010,8(4):362-371.) |