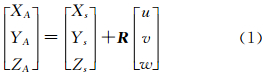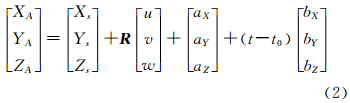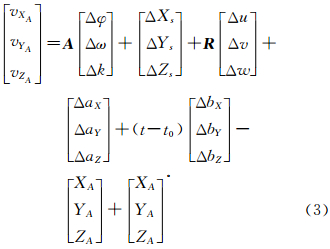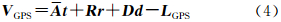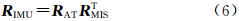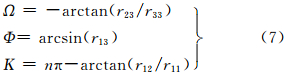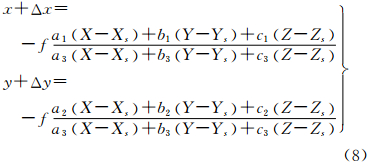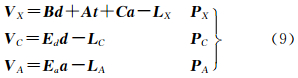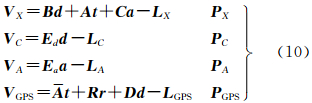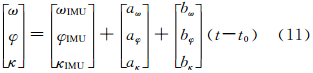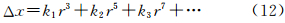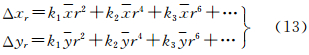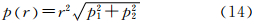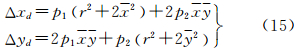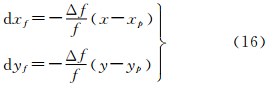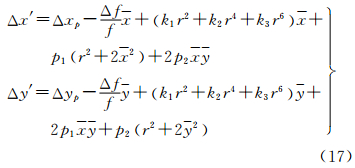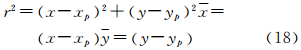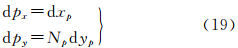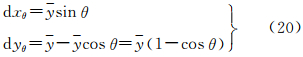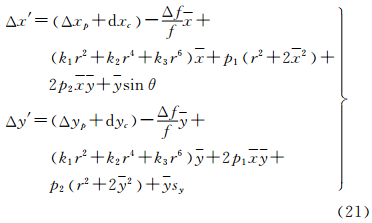1 引 言
发展和使用CCD数字航空摄影系统是当前摄影测量发展的一个方向。机载数字传感器ADS40(airborne digital sensor)是最具代表性的测量型数字航摄仪之一,它采用三线阵CCD扫描成像模式,并通过集成POS(positioning and orientation system),能够在航空摄影的同时记录成像时刻影像外方位元素[1]。
为精确测定传感器成像参数,航测仪出厂前要在实验室经过严格标定,但由于难以顾及温度、气压、平台震颤等动态成像影响因素,难免出现偏差;同时长期使用造成的损耗及老化,也会使成像参数发生变化。因此如何准确、及时获取航摄条件下成像参数是实现影像高精度定位的关键,采用航摄飞行标定是切实可行的方法。国内外曾针对传统胶片式模拟相机进行过大量研究和实践,但机载线阵CCD传感器在成像特性和作业流程上与传统方式有较大区别,集成POS系统也带来传感器空间关系测定等问题,标定内容多,解算难度大,现有的标定方法难以完全适用。
欧洲空间数据研究中心EuroSDR、瑞士苏黎世理工大学、Leica公司等国外有关单位积极开展了机载数字传感器的性能评估与几何标定工作[2, 3, 4, 5, 6, 7, 8, 9]。针对ADS40,文献[10]介绍了Leica公司进行几何标定的原则、方法和主要步骤;文献[11, 12, 13, 14, 15, 16]等则从影像自检校平差的角度分别就平差模型构建、附加参数设置、精度分析和评估等方面进行了研究和试验。文献[17]基于自检校技术设计了ADS40相机检校方案,并基于ORIMA软件系统进行了试验,效果明显。但总体看该技术领域的研究和发展尚不成熟,在模型设置、参数解算等具体技术环节上仍有待深入探讨,尤其缺乏针对机载线阵CCD传感器的专项研究。为此,本文从分析ADS40集成传感器成像几何关系入手,引入GPS观测值数学模型、IMU视轴偏心角模型,在此基础上根据机载三线阵传感器成像误差特性分析设计了相机自检校误差参数模型以及用于标定的自检校光束法区域网平差模型,并以登封遥感检校场ADS40数据来验证所建立模型的正确性和方法的可行性。
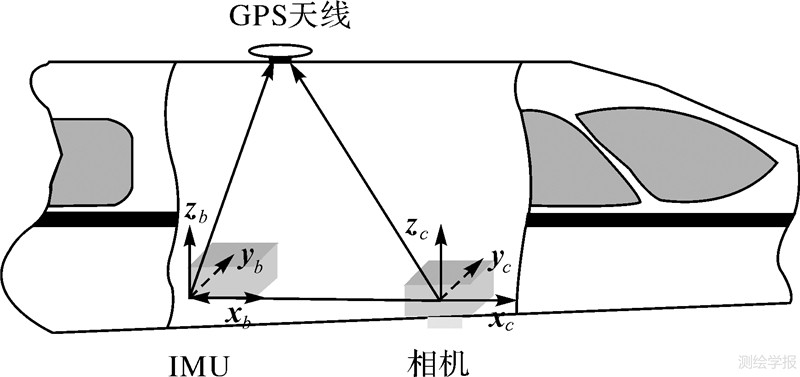
2 ADS40集成传感器成像几何关系ADS40为三线阵扫描航摄仪,集成有GPS/IMU系统(图 1)。为能直接测量外方位元素,最理想的安装方式是将机载GPS天线和IMU安置在摄影相机物镜的后节点上,且使IMU三轴线Xb,Yb,Zb与相机坐标轴Xc,Yc,Zc严格平行,但在实际应用中却不可能完全做到。因此GPS天线相位中心相对相机投影中心总会存在固定的位置偏移,称为GPS偏心矢量;而IMU坐标轴与相机轴线之间总会存在微小的角度差,称为IMU视轴偏心角。同时GPS和IMU系统还都存在漂移特性,尤以IMU为甚,称为漂移误差,仅利用IMU与GPS数据进行卡尔曼滤波难以完全消除。在实际应用中,GPS偏心矢量可在航空摄影前通过地面测量得到,并在后处理过程中予以改正;IMU轴线一般不可视,难以直接测量偏心角,必须通过航摄飞行进行标定。因此对集成传感器航空遥感系统,除了要进行摄影相机成像参数标定外,如镜头畸变、CCD变形和移位等,还包括GPS、IMU与相机空间相对方位的解算和确定。
|
| 图 1 GPS/IMU辅助航空摄影系统 Fig. 1 Aerial photography system equipped with GPS/IMU |
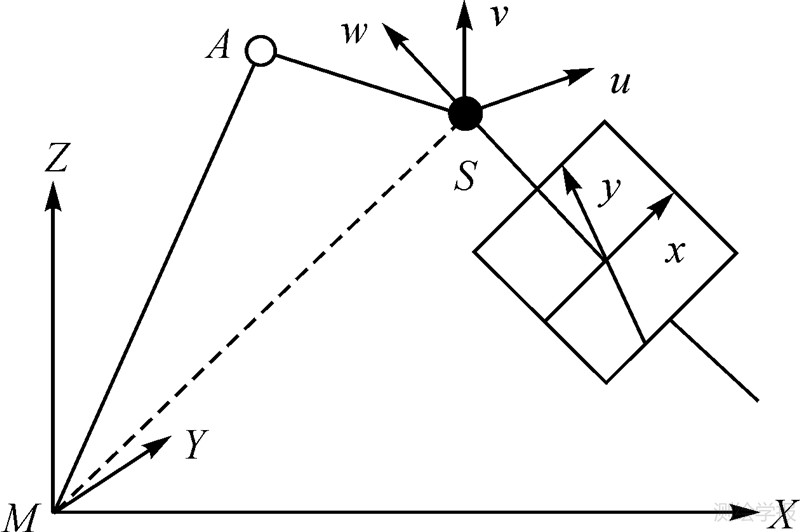
如图 2所示,设GPS天线相位中心A点在像空间辅助坐标系S-uvw中的坐标为(u,v,w),则有
|
| 图 2 机载GPS定位原理 Fig. 2 Positioning principle of aerial system with GPS |
基于载波相位观测量的动态GPS定位,在时间不太长的航摄飞行中,会产生随航摄时间线性变化的系统误差[19],一般称为GPS平移和漂移误差,在式(1)中引入该系统误差改正模型
式中,t0为参考时刻; aX、ay、aZ、bX、by、bZ统称为摄站坐标的系统漂移参数。将GPS摄站坐标引入后会增加偏心分量u、ν、w和线性漂移误差改正参数等未知数。于是GPS摄站坐标误差方程形式为
式中,A为GPS摄站坐标XA、YA、ZA对未知数φ、ω、κ所求一阶偏导数,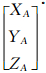 为未知数近似值代入式(2)求得的GPS摄站坐标。
为未知数近似值代入式(2)求得的GPS摄站坐标。
上式写成矩阵形式为
它是GPS摄站坐标的观测方程,式中,VGPS为GPS摄站观测坐标值的改正数向量;t为像片外方位元素未知数的增量向量;r为偏心分量未知数的增量向量;d为线性漂移误差改正数向量;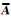 为对应于t的系数矩阵;R为对应于r的系数矩阵;D为对应于d的系数矩阵;LGPS为GPS摄站坐标观测值的常数项向量。
为对应于t的系数矩阵;R为对应于r的系数矩阵;D为对应于d的系数矩阵;LGPS为GPS摄站坐标观测值的常数项向量。
设外方位角元素(ω,φ,κ)构成的旋转矩阵为RAT,IMU角方位元素观测值(Ω,Φ,Κ)构成的旋转矩阵为RIMU,IMU偏心角(ex,ey,ez)构成的旋转矩阵为RMIS,且RAT、RIMU与RMIS之间满足如下关系
即
不妨设上式中的各旋转角均采用ω-φ-κ角元素系统,考虑到Ω、Φ一般数值较小,于是可求出(Ω,Φ,Κ)
对于K角,可根据r12和r11确定整数n的数值。式(7)即为IMU角度观测值的偏心角模型。
3 用于标定的自检校光束法区域网平差自检校技术是解析摄影测量平差中最有效的系统误差补偿方法,它把可能存在的系统误差作为待定参数,列入区域网空中三角测量的整体平差运算之中,对主参数和系统误差参数同时进行最优估计并评定精度,以达到消除或减弱系统误差的目的,其中最适宜引入附加参数的是光束法区域网平差。如果从传感器成像的几何及物理因素出发,使自检校附加参数能正确反映传感器内方位元素、摄影物镜光学畸变等系统性误差因素,并通过区域网平差等方法精确解求各项参数,即可实现基于自检校的传感器几何标定。
3.1 基本误差方程基于附加参数的自检校光束法平差的基本公式为
式中,Δx、Δy代表该像点处引入的附加参数函数。将控制点也处理成带权观测值,则平差基本误差方程式为
式中,VX、VC、VA分别为像点坐标、地面控制点坐标和自检校参数观测值改正数向量;d=[ΔXΔYΔZ]T为物方点坐标未知数增量向量;t=[Δφ Δω Δκ ΔXs ΔYs ΔZs]T为外方位元素未知数增量向量;a=[a1 a2 a3 …]T为自检校附加参数向量;A、B、C为相应于未知数t、d、a的系数矩阵;Ed、Ea为单位矩阵;LX、LC、LA为相应观测值残差向量;PX、PC、PA为相应观测值的权矩阵。
3.2 用于标定的自检校区域网平差模型如何在自检校区域网平差中引入POS数据是关键性问题之一。三线阵传感器定向参数众多,且每个采样周期都对应一套外方位元素,解算过程中不可能、也无必要一一求解,因此选择合适的描述外方位元素变化的轨道模型十分关键。三线阵影像平差常采用定向片法,即在飞行轨道上按一定时间间隔抽取若干离散的扫描周期,称为定向片,并将定向片时刻的外方位元素作为平差未知数进行解求,然后内插出其他采样时刻的外方位元素。该方法优势在于便于引入GPS/IMU观测值且方式灵活,可直接将GPS/IMU测量值作为外方位元素观测值,也可同时考虑其系统性误差改正。如果将GPS观测值数学模型引入自检校平差,则误差方程式在公式(9)的基础上变为
式中,r为偏心分量未知数的增量向量;d为线性漂移误差改正数向量;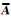 、R、D为GPS摄站坐标误差方程式对应于t、r、d未知数的系数矩阵。若GPS偏心分量事先用地面测量手段精确测得,则r为零;如果进行IMU偏心角的联合标定,直接应用式(7)的偏心角模型比较复杂,且涉及大量的三角函数计算,同时当航偏角k接近90°时,式(7)中的r11≈0,此时r11较小的误差或数值舍入会使结果偏差很大,误差方程状态较不稳定,极有可能出现迭代不收敛的情况。简单起见,也可采用类似GPS系统误差改正的方式,将IMU视准轴误差视为系统偏移和漂移处理,则IMU测量误差改正模型可表示为
、R、D为GPS摄站坐标误差方程式对应于t、r、d未知数的系数矩阵。若GPS偏心分量事先用地面测量手段精确测得,则r为零;如果进行IMU偏心角的联合标定,直接应用式(7)的偏心角模型比较复杂,且涉及大量的三角函数计算,同时当航偏角k接近90°时,式(7)中的r11≈0,此时r11较小的误差或数值舍入会使结果偏差很大,误差方程状态较不稳定,极有可能出现迭代不收敛的情况。简单起见,也可采用类似GPS系统误差改正的方式,将IMU视准轴误差视为系统偏移和漂移处理,则IMU测量误差改正模型可表示为
式中,(aω,aφ,aκ,bω,bφ,bκ)统称为IMU姿态角的漂移误差改正参数。在式(10)基础上引入式(11),则平差基本误差方程式为
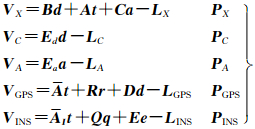
式中,q为偏心角分量未知数的增量向量;e为线性漂移误差改正数向量;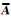 I、Q、E为IMU观测值误差方程式对应于t、q、e未知数的系数矩阵。
I、Q、E为IMU观测值误差方程式对应于t、q、e未知数的系数矩阵。
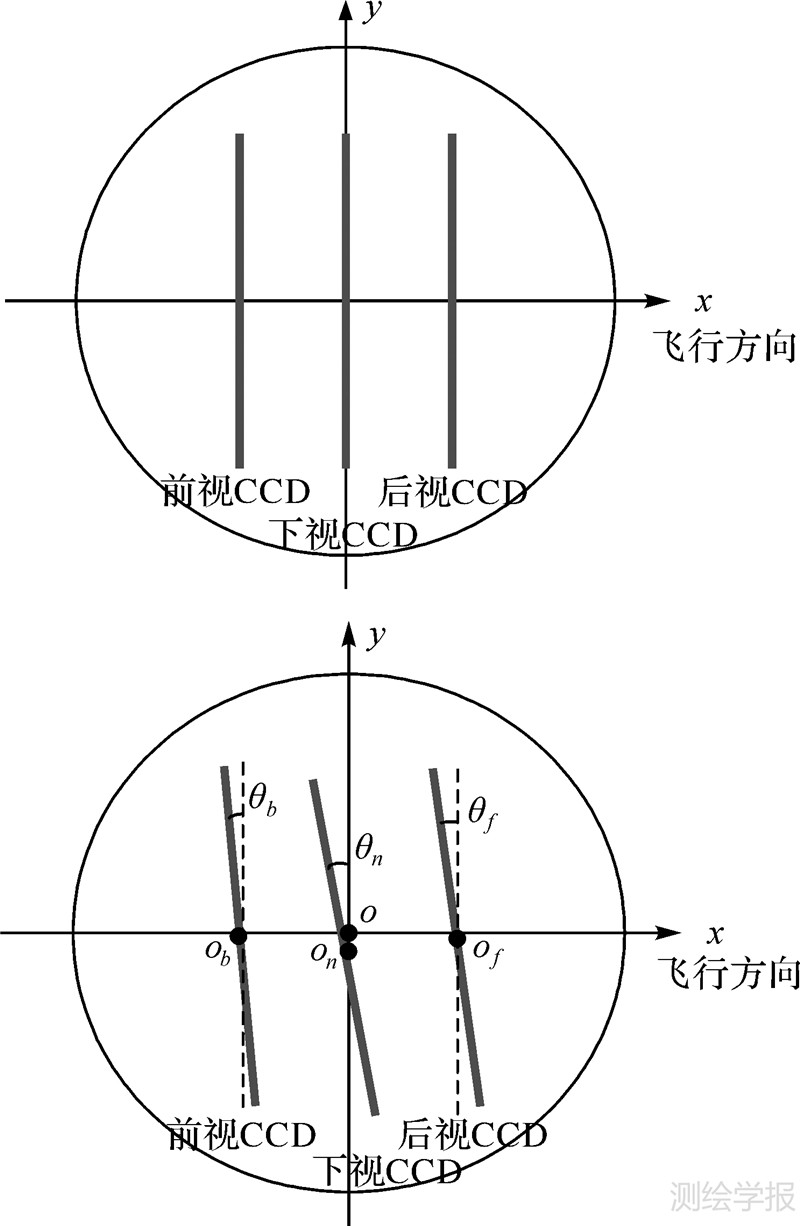
数字航测相机没有框标概念,成像面上各CCD单元的焦面坐标仅能通过实验室和外场检校获得,在动态航摄条件下由于受环境影响,或相机长时间使用等原因,部分CCD像元或会发生几何形变和位置错移,CCD阵列在焦平面内则可能整体平移和旋转,或发生离焦偏移,其对三线阵CCD传感器的影响变化如图 3所示。可见线阵CCD传感器成像关系复杂,误差因素多。如何从传感器成像的几何及物理因素出发,建立合理有效的像差描述模型,使自检校附加参数能正确反映传感器成像特性,是进行几何标定的重要前提。
|
| 图 3 三线阵CCD在焦平面内的平移与旋转 Fig. 3 Translation and rotation of three linear CCD in focal plane |
镜头光学畸变差是指相机物镜系统设计、制作和装配引起的像点偏离其理想位置的点位误差。它是非线性的,主要包括径向畸变和偏心畸变。径向畸变可用下述奇次多项式表示
分别将其分解到像平面坐标系的x轴和y轴上,则有
式中,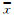 =(x-x0),
=(x-x0),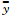 =(x-y0),r2=
=(x-y0),r2=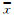 2+
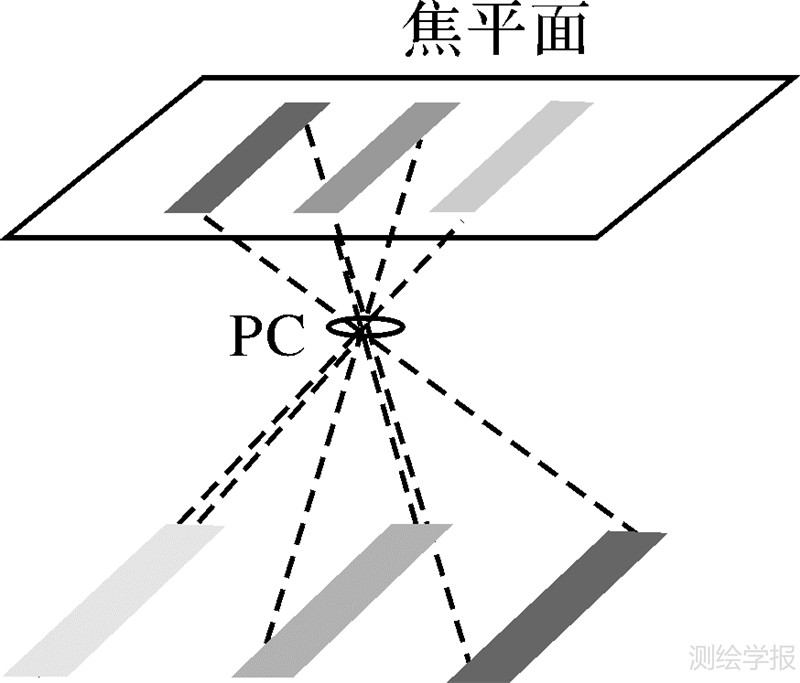
2+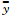 2,(x0,y0)为像主点坐标;k1、k2、k3为径向畸变系数。
2,(x0,y0)为像主点坐标;k1、k2、k3为径向畸变系数。
偏心畸变主要是由光学系统光心与几何中心不一致造成的,即镜头器件的光学中心不能严格共线。偏心畸变使像点既产生径向偏差又产生切向偏差,表达式如下
将其分解到像平面坐标系的x轴和y轴上,则有
式中,p1、p2为偏心畸变系数,偏心畸变在数量上要比径向畸变小得多。
传感器镜头主点坐标xp,yp的偏移,该偏移量在x、y方向上的偏移量用常量Δxp、Δyp表示,同时,设传感器焦距的变化量为Δf,该变化量在像点上的影响可以模拟为
因此对于某像点p,镜头畸变造成的像点误差模型为
式中
4.2 线阵CCD畸变和移位引起像点变化的分析像元尺寸变化主要影响成像比例尺。如图 4所示,建立线阵CCD扫描线坐标系,x轴为飞行方向,y轴为CCD扫描方向(以下同),Np为线阵CCD像元数。设单像元原尺寸为px,py,变化率为dxp,dyp,沿x和y轴方向总变化为dpx,dpy,由于沿y轴方向有Np个像元,x轴方向仅有1个像元,显然有

|
| 图 4 线阵CCD像元尺寸变化的影响 Fig. 4 Linear CCD pixel size change effect |
因此可以只考虑沿y轴方向的变形影响,忽略x轴方向。
CCD在焦平面内的平移将使得像主点偏离原定位置,沿x和y轴方向的移动影响可用常量dxc和dyc表示,如图 5所示。

|
| 图 5 线阵CCD沿y轴和x轴平移 Fig. 5 Translation of linear CCD along x axis and y axis respectively |
设线性CCD在焦平面内旋转了角度θ,dxθ和dyθ分别为由于CCD旋转而造成的在飞行方向和扫描方向的像坐标误差,如图 6所示,则有
|
| 图 6 线阵CCD在焦平面内的旋转 Fig. 6 Rotation of linear CCD in focal plane |
一般情况下dyθ很小,常不予考虑,只进行x轴方向的改正。
因此对单线阵CCD,在考虑沿y轴方向的比例尺变化影响,线阵CCD在焦平面内的平移影响、沿x轴方向的旋转影响后像点误差模型为
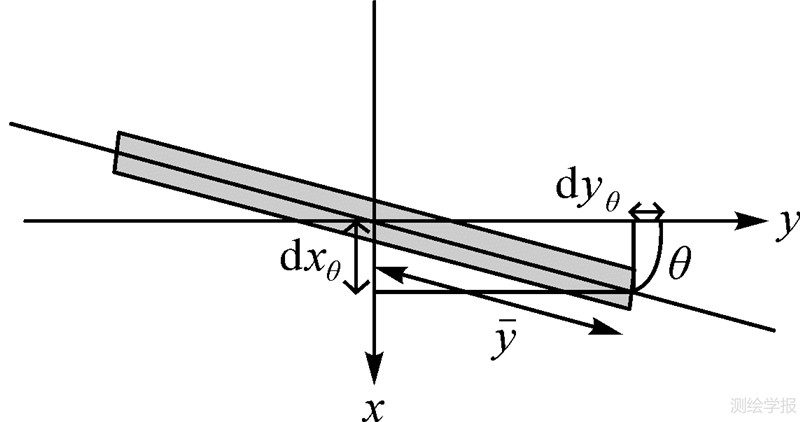
式中,dxc和dyc可合并到主点坐标偏移量中Δxp、Δyp中;θ为线性CCD在焦平面内旋转的角度;sy为比例因子。ADS40采用单镜头多线阵传感器(图 7),各线阵安置在同一焦平面上,共用一套光学系统,因此采用同一组光学畸变系数。对线阵CCDj,j=1,2,3,dxcj和dycj合并到主点坐标偏移量中Δxpj、Δypj中,旋转角度为θj,比例因子为sy j ,则有
|
| 图 7 单镜头多线阵CCD传感器图 Fig. 7 Figure of single lens with multi-CCD |
试验采用2009年8月获取的河南登封遥感检校场ADS40航摄数据。选其中3个架次的数据用于本文试验,相对航高分别为600 m、1000 m和3000 m,对应的像素分辨率GSD分别为0.06 m、0.10 m和0.30 m,分记为数据A、B和C。从数据A选取4条东西航线和2条南北构架航线,影像覆盖区内共选取控制点67个;从数据B选取4条东西航线和2条构架航线,选取控制点43个;从数据C选取7条东西方向平行航线以及4条南北方向构架航线,实际量测地面标志点71个。
5.2 标定方法与步骤采用自行研制的ADS40数据处理软件进行自检校区域网平差标定试验。平差采用定向片模型及式(22)相机误差模型。
步骤1:对数据A、B、C分别利用相机原始检校文件(记为cam0)和同时获取的POS数据进行影像直接定位试验,评定定位精度,分析系统误差状况。
步骤2:分别选取数据A和B进行不同控制条件下的常规光束法区域网平差,进行精度评定;在相同情况下进行自检校光束法区域网平差,对结果进行比对分析。
步骤3:分别从两组自检校区域网平差中选取最优项,并从中提取自检校参数,根据式(22)换算为像点坐标的附加值Δx、Δy,并以此更新相机原始检校文件,分别记为camA和camB。
5.3 几何标定验证验证1:以camA和camB分别代替cam0,其余条件不变,再对A、B、C进行影像直接定位试验,与试验步骤1所得结果进行比较分析,验证几何标定效果。
验证2:以camA和camB分别代替cam0,其余条件不变,再对A、B进行常规光束法区域网平差,与试验步骤2所得结果进行比较分析,验证几何标定效果。
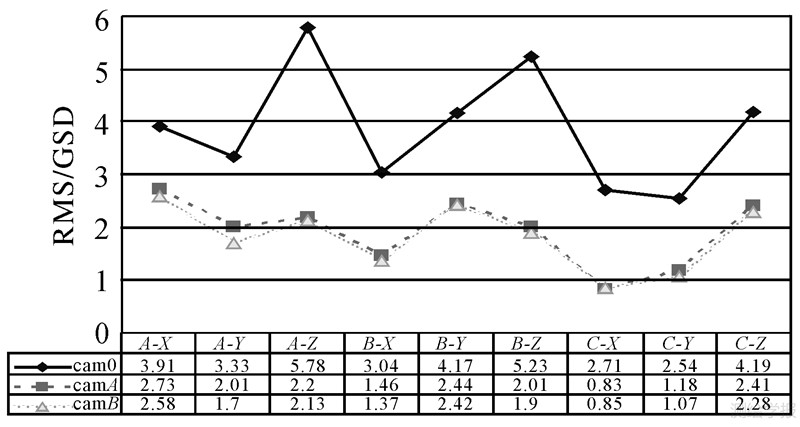
5.4 试验结果与分析表 1是数据A、B进行两种方式区域网平差的结果,对两组数据在相同条件下分别进行常规区域网平差和自检校区域网平差,并试验了不同控制点数量的配置以评估两种平差方法解算精度对地面控制的依赖性;表 2是采用cam0、camA和camB,分别对3组数据进行直接定位的结果;图 8换算为GSD以便于比较;表 3是标定后采用camA和camB在同样条件下再对A和B进行常规区域网平差的结果。
| m | ||||||||
| 数据 | 常规区域网平差 | 自检校区域网平差 | ||||||
| GCP | 检查点均方根 | GCP | 检查点均方根 | |||||
| X | Y | Z | X | Y | Z | |||
| A | 3 | 0.108 | 0.166 | 0.163 | 3 | 0.032 | 0.043 | 0.051 |
| 5 | 0.067 | 0.158 | 0.126 | 5 | 0.024 | 0.039 | 0.047 | |
| 9 | 0.064 | 0.160 | 0.125 | 9 | 0.023 | 0.034 | 0.046 | |
| B | 3 | 0.089 | 0.207 | 0.221 | 3 | 0.039 | 0.062 | 0.082 |
| 5 | 0.084 | 0.198 | 0.211 | 5 | 0.037 | 0.055 | 0.077 | |
| 9 | 0.087 | 0.126 | 0.205 | 9 | 0.036 | 0.045 | 0.074 | |
| 检校 文件 | 数据A | 数据B | 数据C | ||||||
| 检查点均方根 | 检查点均方根 | 检查点均方根 | |||||||
| X | Y | Z | X | Y | Z | X | Y | Z | |
| cam0 | 0.235 | 0.200 | 0.349 | 0.304 | 0.417 | 0.523 | 0.814 | 0.763 | 1.258 |
| camA | 0.164 | 0.121 | 0.132 | 0.146 | 0.244 | 0.201 | 0.249 | 0.354 | 0.723 |
| camB | 0.155 | 0.102 | 0.128 | 0.137 | 0.242 | 0.190 | 0.256 | 0.322 | 0.686 |
|
| 图 8 数据A、B、C直接定位结果 Fig. 8 Direct geopositioning results of data A, B and C sets |
| m | ||||||||
| 数据 | 数据A | 数据B | ||||||
| GCP | 检查点均方根 | GCP | 检查点均方根 | |||||
| X | Y | Z | X | Y | Z | |||
| camA | 3 | 0.037 | 0.051 | 0.062 | 3 | 0.044 | 0.069 | 0.101 |
| 5 | 0.028 | 0.041 | 0.052 | 5 | 0.041 | 0.062 | 0.089 | |
| 9 | 0.023 | 0.034 | 0.053 | 9 | 0.042 | 0.053 | 0.089 | |
| camB | 3 | 0.035 | 0.047 | 0.055 | 3 | 0.042 | 0.064 | 0.091 |
| 5 | 0.029 | 0.038 | 0.051 | 5 | 0.039 | 0.056 | 0.087 | |
| 9 | 0.021 | 0.034 | 0.048 | 9 | 0.037 | 0.044 | 0.089 | |
分析发现:
(1) ADS40影像直接定位精度不高,平面X方向约为2.71~3.91个GSD,Y方向约为2.54~4.17个GSD,Z方向较差,在4.19~5.78个GSD之间。分析其误差应主要源于两方面:一是内方位成像参数变化对像坐标的影响;二是外方位元素观测数据中GPS偏心、IMU偏心角及系统漂移等所引入的系统性误差。
(2) 从表 1看,影像区域网平差对控制点数量要求不高,5个以上即可得到稳定的结果,更多的控制点对结果改善效果不明显;当采用自检校区域网平差时能显著提升定位精度,在采用9控制点平差趋于稳定,此时数据A的X、Y、Z方向的精度由1.0、2.6和2.1个GSD分别提高到0.4、0.6和0.8个GSD,而数据B则由0.9、1.3和2.0个GSD提高到0.4、0.5和0.7个GSD,两组试验结果相近,在平面Y方向改善效果最为明显;该试验表明常规光束法平差因存在系统误差影响而难以达到理想精度,采用自检校区域网平差能对系统误差的有效补偿,显著提升定位精度,可用于传感器几何标定。
(3) 采用camA和camB对数据A、B再次进行直接定位的结果表明,利用标定参数更新检校文件后,直接定位的精度得到了大幅提高,在改善程度上两者比较接近,camB略优于camA,其中精度改善在Z方向上最为明显,最大在3.6个GSD以上,最小也有1.8个GSD,平面X方向精度提升幅度约为1.2~1.8个GSD,Y方向幅度约为1.3~1.7个GSD。
(4) 采用camA和camB对数据A、B再次进行区域网平差的结果表明,检校文件更新后,常规区域网平差的精度得到显著提升,与同等控制条件下采用cam0 文件进行自检校区域网平差的结果相比,差距也已经非常小。
(5) 标定后影像直接定位的绝对精度相比标定前常规区域网平差精度仍有差距,表明ADS40直接定位的精度主要决定于POS数据的精度;但在少量地面控制点支持下,进行标定后采用常规区域网平差即可得到理想的定位精度。
以上试验表明,ADS40相机经几何标定后影像定位精度得到显著改善和提高,本文提出和建立的基于自检校的机载线阵CCD传感器几何标定的模型与方法是可行有效的。但受相关条件制约,仅对单台ADS40相机进行了标定试验,所用数据也比较有限,缺少不同地形区域、不同时间周期的全面数据,有待进一步扩大试验并进行深入研究。
| [1] | SANDAU R, BRAUNECKER B, DRIESCHER H, et al.Design Principles of the LH Systems ADS40 Airborne Digital Sensor[C]//Proceedings of International Archives of Photogrammetry and Remote Sensing. Amsterdam: IAPRS, 2000:258-265. |
| [2] | CRAMER M. A European Network on Camera Calibration [J]. Photogrammetric Engineering and Remote Sensing, 2004, 70 (12):1328-1334. |
| [3] | CRAMER M. Calibration and Validation of Digital Airborne Cameras [C]//Proceedings of the International Calibration and Orientation Workshop EuroCOW 2006. Castelldefels:[s.n.], 2006. |
| [4] | CRAMER M. The EuroSDR Approach on Digital Airborne Camera Calibration and Certification [C]//Proceedings of the International Archives of the Photogrammetry, Remote Sensing and Spatial Information Sciences .Beijing:IAPRS, 2008:1753-1758. |
| [5] | MOSTAFA M R. Digital Multi-sensor Systems-calibration and Performance Analysis[C]//Proceedings of OEEPE Workshop Integrated Sensor Orientation. Hannover:[s.n.],2001:17-18. |
| [6] | PACEY R E, WALKER A S, SCHEIDT M. Calibration of Analogue and Digital Airborne Sensors at LH Systems[C]//Proceedings of the 1999 ASPRS Annual Conference. Portland:[s.n.],1999: 950-956. |
| [7] | PETRIE G A, WALKER S. Airborne Digital Imaging Technology: a New Overview [J]. The Photogrammetric Record, 2007, 22(119):203-225. |
| [8] | HONKAVARRA E, AHOKAS E, HYYPPA J, et al. Geometric Test Field Calibration of Digital Photogrammetric Sensors[J]. ISPRS Journal of Photogrammetry and Remote Sensing,2006, 60(6):387-399. |
| [9] | DOERSTEL C, ZEITLER W. Geometric Calibration of the DMC: Method and Results [C]//Proceedings of Pecora 15/Land Satellite Information IV/ISPRS Commission I/FIEOS 2002 Conference .[S.l.]:IAPRS, 2002:324-333. |
| [10] | TEMPELMANN U, HINSKEN L, RECKE U. ADS40 Calibration and Verification Process[C]//Proceedings of Optical 3D Measurement Techniques Conference.Zurich:[s.n.], 2003:48-54. |
| [11] | KOCAMAN S, CASELLA V, FRANZINI M, et al.The Triangulation Accuracy of ADS40 Imagery over The Pavia Testsite[C]//Proceedings of WG 4 “Airborne Digital Photogrammetric Sensor Systems” Workshop. Newcastle:[s.n.], 2007:12-17. |
| [12] | CASELLA V, FRANZINI M, KOCAMAN, et al.Triangulation and Self-calibration of the ADS40 Imagery: a Case Study over the Pavia Test Site[C]//Proceedings of the 8th Conference on “Optical 3D Measurement Techniques”. Zurich:[s.n.], 2007:223-232. |
| [13] | LIU Jun,WANG Donghong, ZHANG Yongsheng. Triangulation of ADS40 Three Line Images Using Unit Quaternion [C]//Proceedings of the International Archives of the Photogrammetry, Remote Sensing and Spatial Information Sciences. Beijing:IAPRS, 2008: 573-578. |
| [14] | CRAMER M. The ADS40 Vaihingen/Enz Geometric Performance Test[J]. ISPRS Journal of Photogrammetry and Remote Sensing ,2006, 60(6):363-374. |
| [15] | CRAMER M. Digital Camera Calibration[R]. Frankfurt:EuroSDR ,2009. |
| [16] | KOCAMAN S, ZHANG L, GRUEN A. Self-calibrating Triangulation of Airborne Linear Array CCD Cameras[C]//Proceedings of the EuroCOW 2006 International Calibration and Orientation Workshop . Castelldefels:[s.n.],2006:25-27. |
| [17] | TU Xinru, XU Miaozhong, LIU Li. The Geometric Calibration of Airborne Three-line-scanner ADS40[J]. Acta Geodaetica et Cartographica Sinica, 2011,40(1):78-83(涂辛茹,许妙忠,刘丽. 机载三线阵传感器ADS40的几何检校[J]. 测绘学报,2011,40(1):78-83.) |
| [18] | YUAN Xiuxiao. The Principle and Application of GPS-supported Aerial Triangulation[M]. Beijing: Surveying and Mapping Press. 2001:35-40.(袁修孝. GPS辅助空中三角测量原理及应用[M]. 北京:测绘出版社,2001:35-40.) |
| [19] | FRIESS P.Aerotriangulation with GPS-Methods, Experiences, Exception [C]//Proceedings of the Photogrammetric Week 91.Stuttgart:[s.n.], 1999. |
| [20] | LIU Jun, A Study on the Positioning Theory of Airborne Line CCD Imagery Supported by GPS/IMU[D]. Zhengzhou: Information Engineering University, 2007:41-42. (刘军. GPS/IMU辅助机载线阵CCD影像定定位技术研究[D]. 郑州:信息工程大学,2007:41-42. ) |