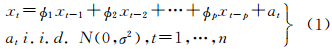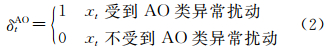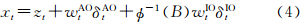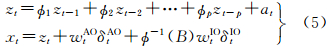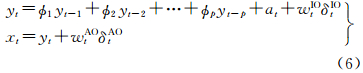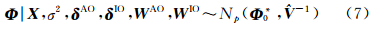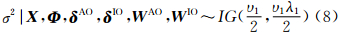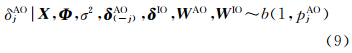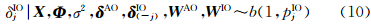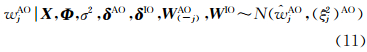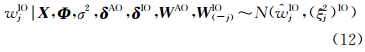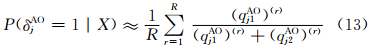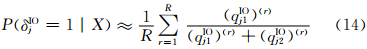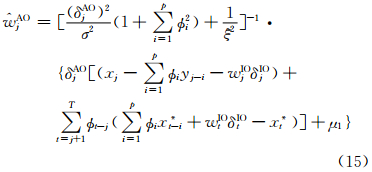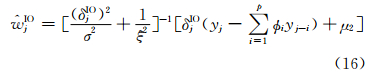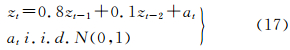2. 信息工程大学 测绘学院,河南 郑州 450052
2.Institute of Surveying and Mapping, Information Engineering University, Zhengzhou 450052 ,China
1 引 言
时间序列分析是测绘导航数据处理的基本技术手段[1, 2],而异常值探测是时间序列分析中的一个重要环节[3, 4, 5, 6, 7, 8, 9, 10]。通常,时间序列中的异常值分为加性异常值和革新异常值两种类型[3, 4]。加性异常值,又称AO类异常值,是指只影响异常干扰发生的那一个时刻的观测值,而不影响该时刻以后的观测值;革新异常值,又称IO类异常值,是指造成这种异常值的干扰不仅作用于该时刻的观测值而且影响该时刻以后的所有观测值。目前,关于自回归模型(自回归模型是时间序列分析中最具代表性的一类线性模型[1, 2])中这两类异常值的探测主要有非Bayesian方法和Bayesian方法。前者主要有迭代似然比法[5],基于稳健估计和影响分析思想的探测法[6]和序贯检验法等[7]。后者主要有文献[3]提出的探测方法,该方法是先探测出AO类异常值,对数据进行修正后,再继续探测IO类异常值,但是该方法未给出明确的异常值探测规则,文献[8]用Gibbs抽样算法讨论了该方法涉及的有关后验概率值的计算问题;文献[9, 10]借鉴文献[11, 12]的思想,在一定限制条件下,将AR模型的异常值探测问题转化为线性模型的异常值探测问题,从而提出了异常值定位和定值的Bayes方法。然而,这些Bayesian方法并没有对定位的异常值进行区分,更未讨论如何解决时间序列中在同一时刻同时出现AO类和IO类异常值这一问题。为此本文通过进一步发展文献[13, 14]的思想,提出一种基于不同类型识别变量,同时探测AR模型中AO类异常值和IO类异常值的Bayes方法。为了验证该方法的正确性,本文进行了大量的模拟试验,并把该方法应用于钟差实测数据的优化处理中,通过比较异常值消除前后各数据点的均方误差,论证了该方法对于解决时间序列数据中在同一时刻或不同时刻出现加性异常值或革新异常值的探测问题是可行和有效的。
2 基于不同类型识别变量的自回归模型异常值定位的Bayes方法设有一组时间序列数据{x1,…,xn}符合如下的AR(p)模型
式中,i.i.d.为相互独立同分布;Φ=[φ1φ2…φp]T和σ2为未知参数。
对每个观测值xt分别引入AO类异常值识别变量
和IO类异常值识别变量
记w1AO1,…,wnAO和w1IO,…,wnIO分别代表每个时刻观测值的AO类异常值大小和IO类异常值大小,并假设:
(1) 每个观测值xt受到AO类异常扰动或IO类异常扰动的先验概率都为α[3],即P(δtAO=1)=α,P(δtIO=1)=α。
(2) 根据共轭先验分布的选取准则[12, 13, 16]和实际应用的需要,取参数的先验分布为
wtAO i.i.d. N(μ1,ξ2)、wtIO i.i.d. N(μ2,ξ2)、
δtAO i.i.d. b(1,α)、δtIO i.i.d. b(1,α)、
Φ~Np(Φ0,V-1)、σ2~IG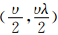 。
。
其中,μ1、μ2、ξ、α、Φ0、V、υ和λ为超参数。
根据以上假设,观测值xt可表示为
式中,zt代表未受到异常扰动的干净数据;φ(B)=I-φ1B-φ2B2-…-φpBp,B为后推算子,即Bkxt=xt-k。式(4)右边的第3项之所以含有因子φ-1(B)是考虑到IO类异常值的定义[3]。由此,可得基于AR模型的AO类和IO类异常值同时探测的模型
为了计算简便,对式(5)进行等价转换,令yt=zt+φ-1(B)wtIOδtIO,则可得与式(5)等价的模型
式中,yt代表仅受到IO类异常扰动的数据。不妨设前p个观测值x1,…,xp为正常值[8],为判定观测值中是否含有AO类或者IO类异常值以及确定它们的判别阈值,构造如下两个Bayes假设检验问题。
原假设H01:xt是正常观测值,即δtAO=0;
备选假设H11:xt为AO类异常值,即δtAO=1。
原假设H02:xt是正常观测值,即δtIO=0;
备选假设H12:xt为AO类异常值,即δtIO=1。
根据Bayes假设检验的思想和原理[16],当备选假设H11对应的后验概率P(δtAO=1|X)大于原假设H01对应的后验概率P(δtAO=0|X),即P(δtAO=1|X)>0.5时,认为备选假设成立,从而认为观测值xt为AO类异常值,反之,认为观测值xt是正常观测值。同理,若P(δIOt=1|X)大于P(δIOt=0|X),即P(δIOt=1|X)>0.5时,认为备选假设成立,从而认为观测值xt为IO类异常值,反之,认为观测值xt是正常观测值。若P(δtAO=1|X)>0.5且P(δIOt=1|X)>0.5,则判断xt同时受到AO和IO两种异常扰动。其中,X=[xp+1xp+2…xn]T。这样,问题归结为计算每个观测值xt含有AO类异常值的后验概率P(δtAO=1|X)和含有IO类异常值的后验概率P(δIOt=1|X)。
3 基于Gibbs抽样的后验概率值的计算和异常值的估计 3.1 参数的完全条件分布由于后验概率P(δtAO=1|X)和P(δtIO=1|X)涉及的分布比较复杂,下面引入Gibbs抽样算法[15]来解决这些后验概率值的计算问题。为此,根据Bayes定理[16]可得下列未知参数的完全条件分布。
(1) X、σ2、δAO、δIO、WAO、WIO给定时,Φ的完全条件分布为
式中
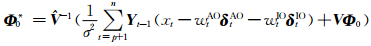
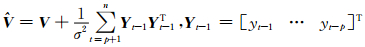
WAO=[w1AO…wnAO]T,WIO=[w1IO…wnIO]T
δAO=[δ1AO…δnAO]T,δIO=[δ1IO…δnIO]T
(2) X、Φ、δAO、δIO、WAO、WIO给定时,σ2的完全条件分布为
式中
υ1=n-p+υ
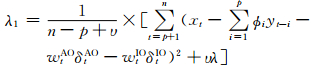
(3) X、Φ、σ2、δ(-j)AO、δIO、WAO、WIO给定时δjAO的完全条件分布为
式中
δ(-j)AO=(δ1AO,…,δj-1AO,δj+1AO,…,δnAO)T
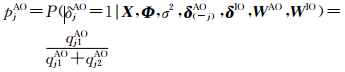
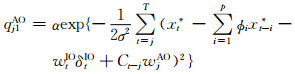
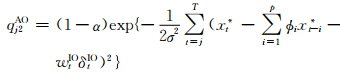
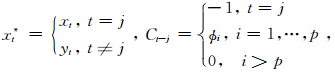
T=min(n,p+j)
(4) X、Φ、σ2、δAO、δ(-j)IO、WAO、WIO给定时,δjIO的完全条件分布为
式中
δ(-j)IO=[δ1IO…δj-1IO δj+1IO…δnIO]T
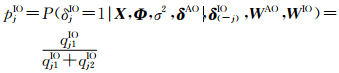
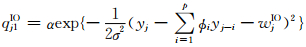
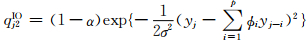
(5) X、Φ、σ2、δAO、δIO、W(-j)AO、WIO给定时,wjAO的完全条件分布为
式中
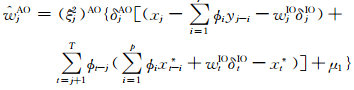
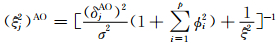
(6) X、Φ、σ2、δAO、δIO、WAO、W-jIO给定时,wIOj的完全条件分布为
式中
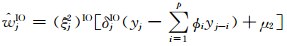
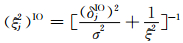
设Φ(r),(σ2)(r),(δAO)(r),(δIO)(r),(WAO)(r),(WIO)(r)r=1,…,R为用Gibbs抽样算法从上述完全条件分布中抽取的样本,则计算AO类异常值和IO类异常值的识别变量后验概率值的公式分别为
和
式中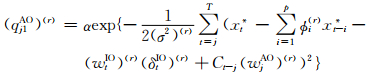
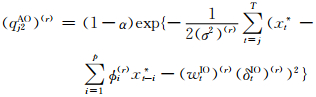
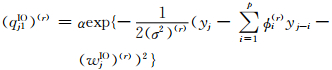
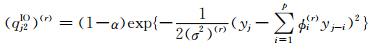
由第2节中的异常值探测模型知,w1AO,…,wnAO和w1IO,…,wnIO分别为AO类和IO类异常值的大小。根据Bayes估计原理[16],取它们的后验均值作为AO类和IO类异常值的估计值,即
4 自回归模型异常值探测的Bayes方法的实施过程第1步,确定先验分布中的超参数。例如,本文在算例1中给出这些超参数的一组具体取值如下
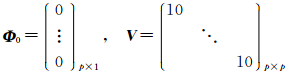
υ=3,λ=0.5,α=0.05,
ξ2=2,μ1=0,μ2=0
第2步,根据Bayes估计方法[16]以及超参数的取值,确定Gibbs抽样的初值。
第3步,假定第s≥1次抽样开始时样本值向量为
(Φ(s-1),(σ2)(s-1),(δAO)(s-1),(δIO)(s-1),(WAO)(s-1),(WIO)(s-1))
则第s次抽样按下列方式产生样本值向量
(Φ(s),(σ2)(s),(δAO)(s),(δIO)(s),(WAO)(s),(WIO)(s))
Φ(s)从以下条件分布中抽取
p(Φ|X,(σ2)(s-1),(δAO)(s-1),(δIO)(s-1),(WAO)(s-1),(WIO)(s-1))
(σ2)(s)从以下条件分布中抽取
p(σ2|X,Φ(s),(δAO)(s-1),(δIO)(s-1),(WAO)(s-1),(WIO)(s-1))
(δjAO)(s)从以下分布中抽取
p(δjAO=1|X,Φ(s),(σ2)(s),(δ(-j)AO)(s-1,j+1),(δIO)(s-1,j),(WAO)(s-1,j),(WIO)(s-1,j))
(wjAO)(s)从以下分布中抽取
p(wAOj|X,Φ(s),(σ2)(s),(δAO)(s-1,j+1),(δIO)(s-1,j),
(W(-j)AO)(s-1,j+1),(WIO)(s-1,j))
(δjIO)(s)从以下分布中抽取
p(δIOj=1|X,Φ(s),(σ2)(s),(δAO)(s-1,j+1),
(δ(-j)IO)(s-1,j+1),(WAO)(s-1,j+1),(WIO)(s-1,j))
(wjIO)(s)从以下分布中抽取
p(wIOj|X,Φ(s),(σ2)(s),(δAO)(s-1,j+1),
(δIO)(s-1,j+1),(WAO)(s-1,j+1),(W(-j)IO)(s-1,j+1))
其中,向量的上角标(i,k)的含义为该向量的第1个分量至第k-1个分量是第i+1次抽样抽取的样本,第k个分量至最后一个分量为第i次抽样抽取的样本。例如
(δAO)(s-1,j+1)=((δ1AO)(s),…,(δjAO)(s),(δj+1AO)(s-1),…,(δnAO)(s-1))T
重复上述抽样过程R次,每次均直到Markov链达到稳定,就得到R个Gibbs样本
(Φ(1),(σ2)(1),(δAO)(1),(δIO)(1),(WAO)(1),(WIO)(1))…(Φ(R),(σ2)(R),(δAO)(R),(δIO)(R),(WAO)(R),(WIO)(R))
第4步,按公式(13)和(14)计算识别变量的后验概率值,并按照第2节中的判别规则进行异常值定位。
第5步,按3.3节中的方法估计异常值的大小。
5 算例与分析 5.1 算例1考虑AR(2)模型
取z1=0.3,z2=0.2,经模拟产生100个数据。采用如下3种方案进行试验和计算。
方案1:在第20个观测值上加大小为-15的IO类异常值。
方案2:在第50个、第80个观测值上分别加大小为10、-6的AO类异常值。
方案3:在第30个观测值上加大小为12的AO类异常值和大小为5的IO类异常值,在第78个观测值上加大小为-9的IO类异常值。
3种方案中异常值识别变量的后验概率值分别如图 1~图 6所示。经判断,方案1中的第20个观测值为IO类异常值,方案2中的第50个、第80个观测值都为AO类异常值,方案3中的第30个观测值同时AO类异常值和IO类异常值,第78个观测值为IO类异常值。又经估计,异常值的大小分别为-14.454 7、9.654 8、-5.235 2、12.908 6、5.906 9、-8.398 7。
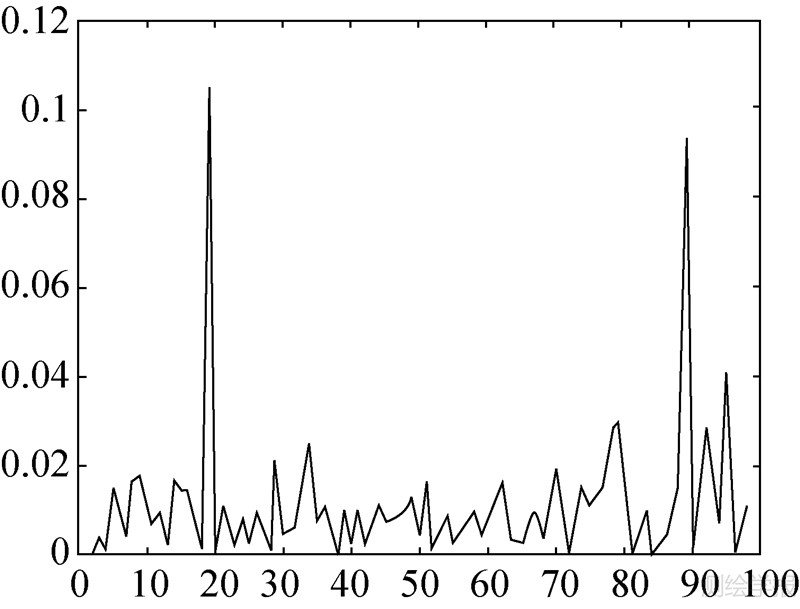
|
| 图 1 AO类异常值识别变量的后验概率值(方案1) Fig. 1 Posterior probability of additive outlier classification variable of scheme 1 |
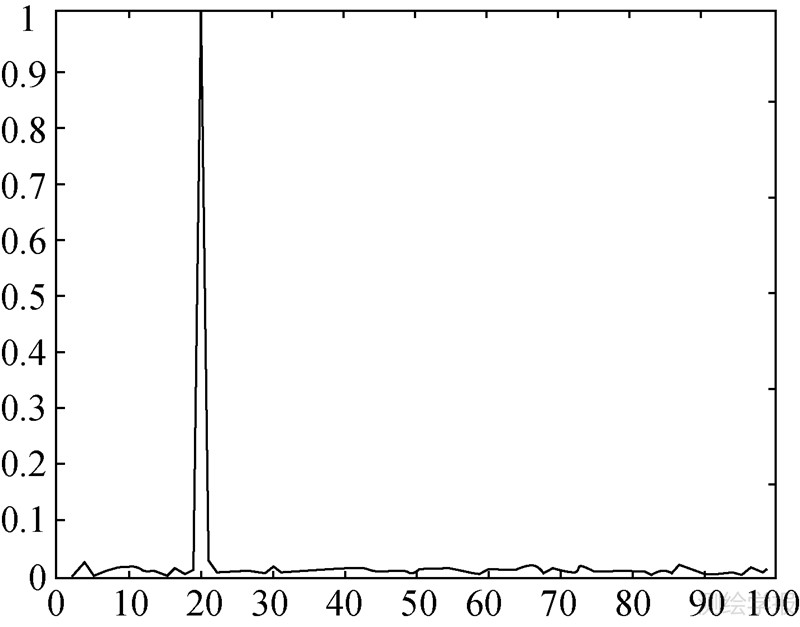
|
| 图 2 IO类异常值识别变量的后验概率值(方案1) Fig. 2 Posterior probability of innovational outlier classification variable of scheme 1 |
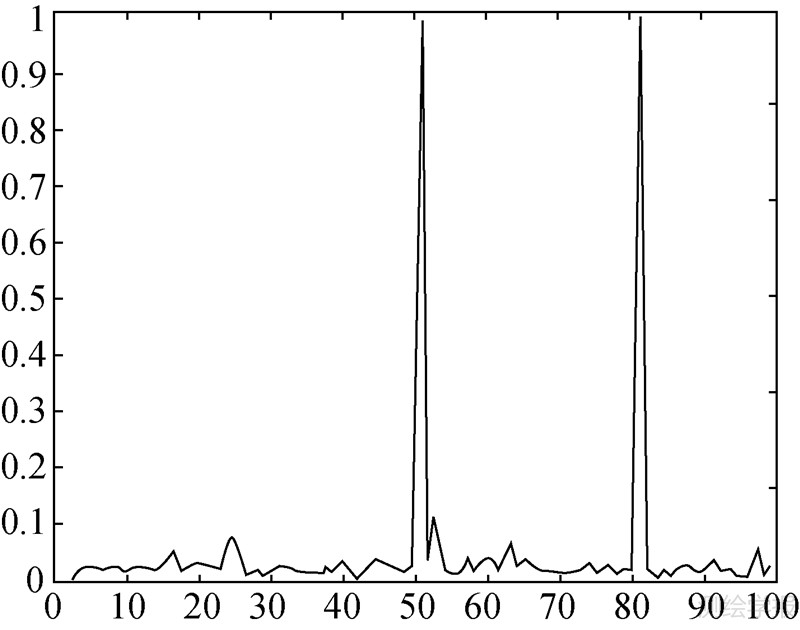
|
| 图 3 AO类异常值识别变量后验概率值(方案2) Fig. 3 Posterior probability of additive outlier classification variable of scheme 2 |
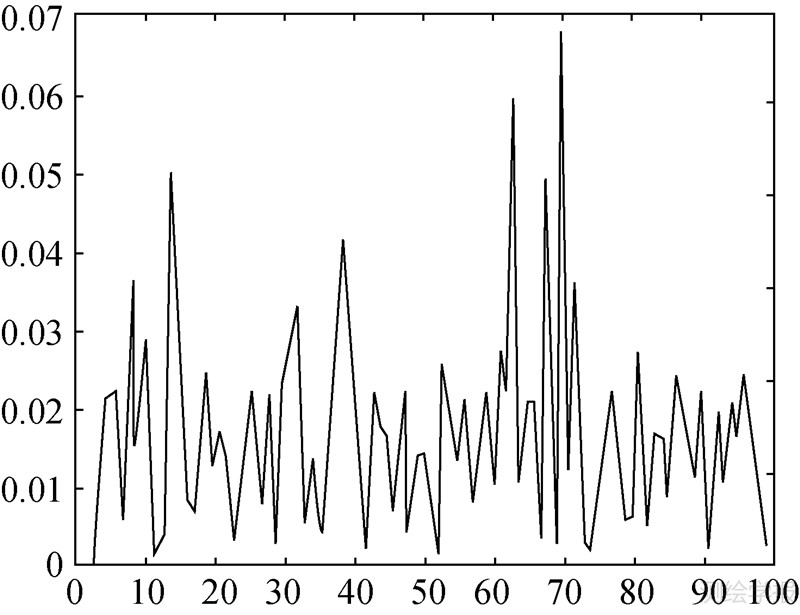
|
| 图 4 IO类异常值识别变量后验概率值(方案2) Fig. 4 Posterior probability of innovational outlier classification variable of scheme 2 |
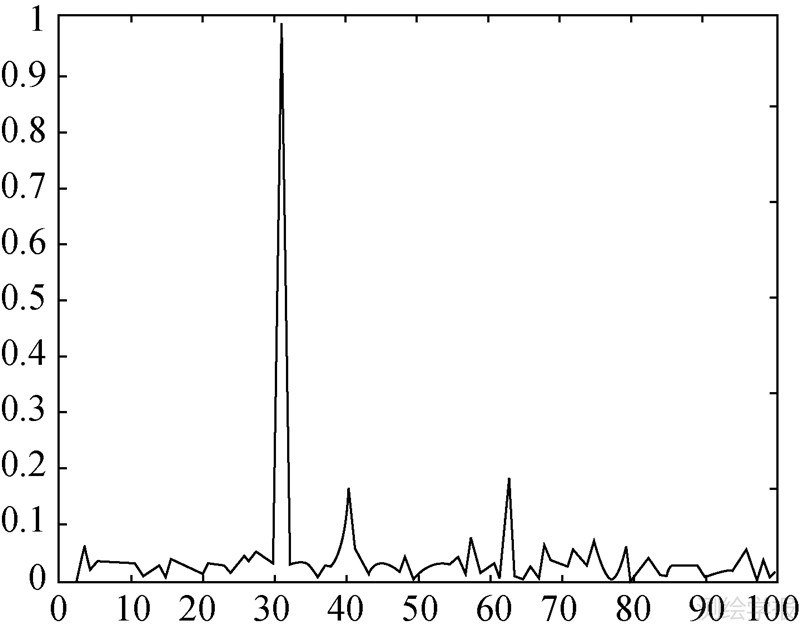
|
| 图 5 AO类异常值识别变量的后验概率值(方案3) Fig. 5 Posterior probability of additive outlier classification variable of scheme 3 |
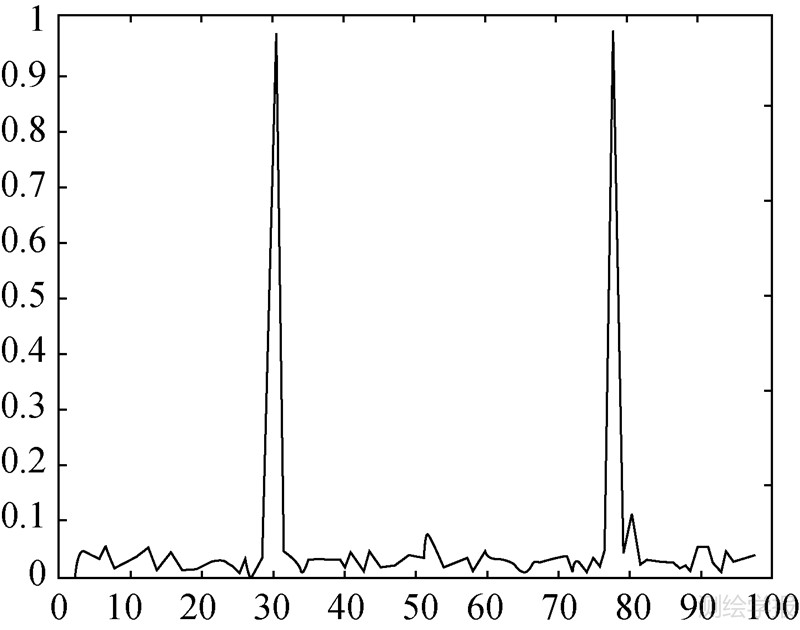
|
| 图 6 IO类异常值识别变量的后验概率值(方案3) Fig. 6 Posterior probability of innovational outlier classification variable of scheme 3 |
由此可见,无论是同一种类型的异常值还是不同类型的异常值,无论它们在同一时刻出现还是在不同时刻出现,利用本文的方法进行定位和定值均能取得很好的效果。
5.2 算例2取IGS发布的2007-07-31全天的一组卫星钟差数据[11],每5 min一个测值,故有288个观测值,如图 7所示。本文对这组观测序列进行异常值探测,并且比较修正前后观测序列的均方误差。
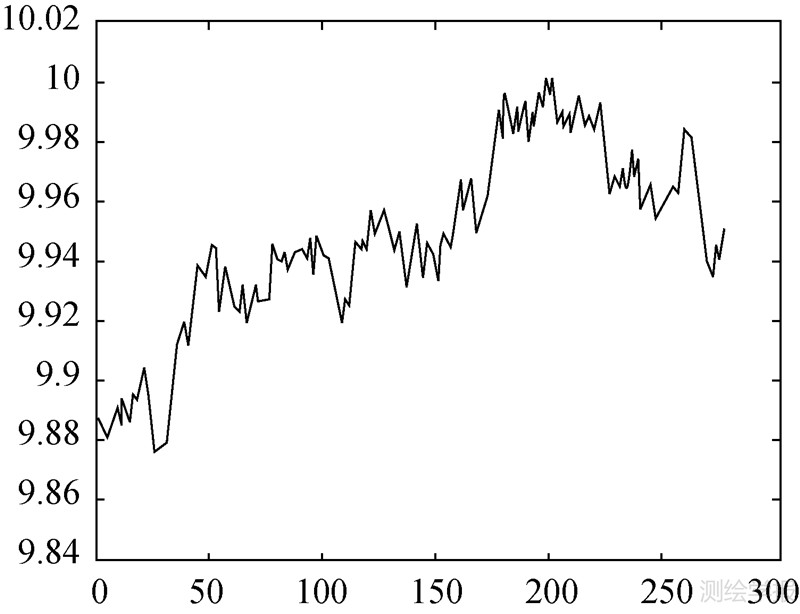
|
| 图 7 原始钟差序列 Fig. 7 Primal observations of satellite clock error |
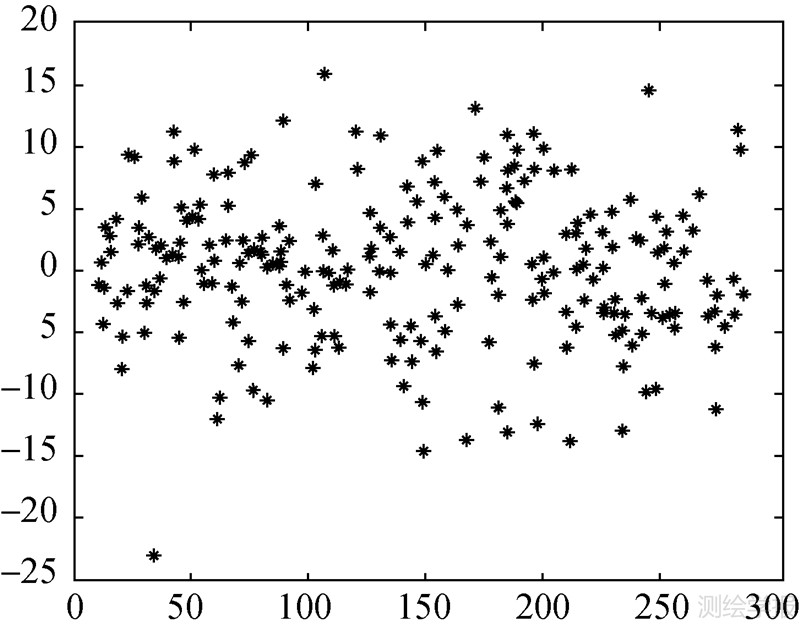
采用参数检验法[17]对钟差序列进行平稳性检验,发现该序列不平稳,为此对该序列进行差分,结果如图 8所示。从图 8可以看出一次差分后的序列为平稳序列。用AIC准则对一次差分后的序列进行模型识别和定阶,发现该序列符合如下的AR(1)模型
|
| 图 8 一次差分后的钟差序列 Fig. 8 Differential observations of satellite clock error |
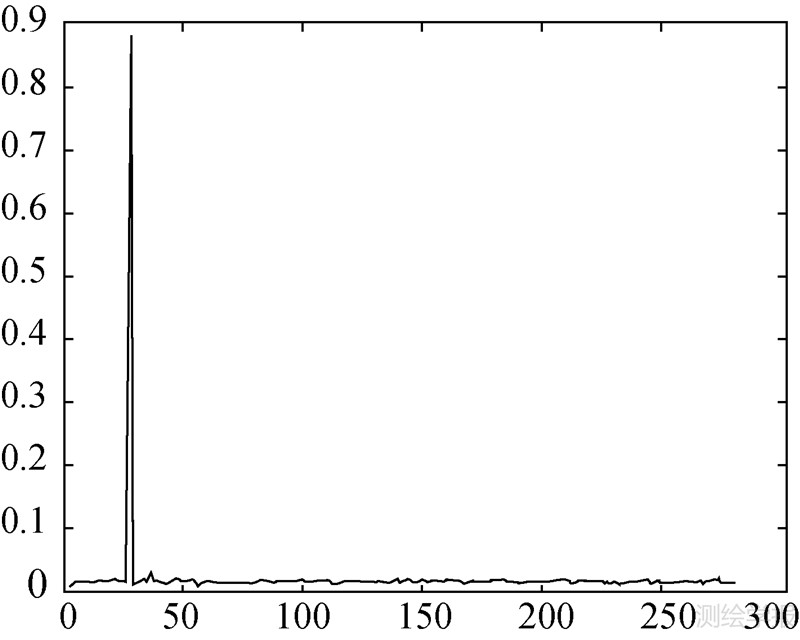
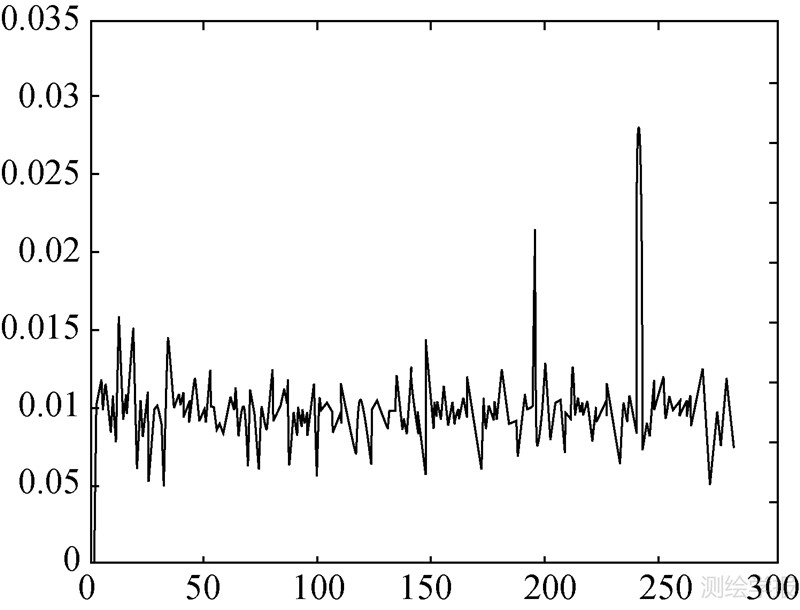
异常值识别变量后验概率值的计算结果如图 9和图 10所示。经判断,第25个观测值为AO类异常值,进一步,其异常扰动的大小估计为wa (25)= -0.022 561 1 ns。
|
| 图 9 AO类异常值识别变量后验概率值 Fig. 9 Posterior probability of additive outlier classification variable |
|
| 图 10 IO类异常值识别变量后验概率值 Fig. 10 Posterior probability of innovational outlier classification variable |
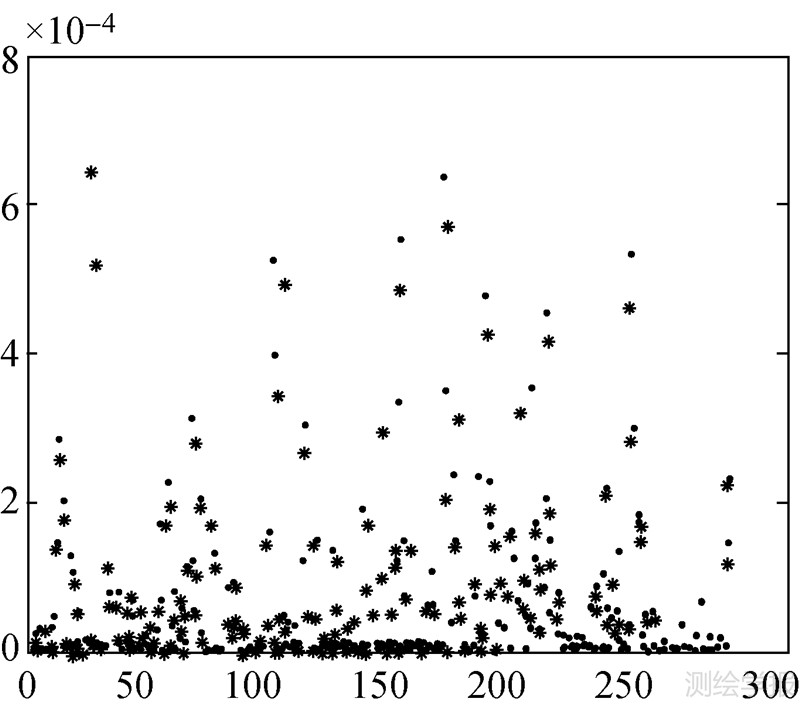
根据AO异常值的定义对第25个数据点进行修正,并比较修正前后各个数据点的均方误差,如图 11所示。可以看出,消除异常值后各个数据点的均方误差的大部分都小于消除异常值前的均方误差。事实上,经统计发现,288个数据点的均方误差中,有215个点的均方误差有所减小,占总数据的70%左右。而且观测值序列总体的均方误差在消除异常值之前为6.493 0e-005,而在消除异常值之后为5.723 0e-005,亦有所减小。
|
| 注:为消除前;*为消除后。 图 11 修正前后各个序列值的均方误差的比较 Fig. 11 Comparison of mean square errors of observations modified and unmodified |
(1) 针对每个时刻观测值中可能含有的不同类型的异常值分别引入不同类型的识别变量,通过比较这些识别变量后验概率值与事先给定的阈值来进行异常值探测,有效地克服了以往探测方法的模糊性及探测标准选择困难的问题,并且较好地解决了时间序列数据中在同一时刻或不同时刻出现不同类型异常值的探测问题。
(2) 在正态-Gamma先验分布下,基于Gibbs抽样算法,提出了识别变量后验概率值的计算方法和异常值的估算方法。
(3) 基于识别变量的自回归模型异常值探测的Bayes方法,较为成功地应用于卫星钟差实测数据的优化处理中,验证了新方法的可行性和有效性。
(4) 根据Bayes假设检验的思想和原理,确定出了异常值判别阈值。
(5) 将Gibbs抽样算法等MCMC现代统计计算方法引入动态测量数据处理中,使得以往认为不可能实施计算的一些方法变得可行,特别对Bayes统计推断理论与方法在动态测量数据处理中的应用开辟了广阔的前景。
| [1] | HUANG Shengxiang,YIN Hui,JIANG Zheng. The Data Processing of Deformation Monitoring[M]. Wuhan:Wuhan University Press, 2003.(黄声享,尹晖,蒋征.变形监测数据处理[M].武汉:武汉大学出版社,2003) |
| [2] | WU Fumei, YANG Yuanxi. Gyroscope Random Drift Model Based on the Higher-order AR Model[J]. Acta Geodaetica et Cartographic Sinica, 2007, 36(4):389-394.(吴富梅,杨元喜.基于高阶AR模型的陀螺随机漂移模型[J].测绘学报,2007, 36(4):389-394.) |
| [3] | ABRAHAM B, BOX G E P. Bayesian Analysis of Some Outlier Problems in Time Series[J]. Biometrika,1979, 66:229-236. |
| [4] | WEI Bocheng, LU Guobin, SHI Jianqing. Introduction to Statistics Diagnose[M].Nanjing: Southeast University Press, 1991.(韦博成,鲁国斌,史建清.统计诊断引论[M].南京:东南大学出版社,1991.) |
| [5] | TSAY R S. Time Series Model Specification in the Presence of Outliers [J]. Journal of American Statistical Association, 1986, 393(81):132-141. |
| [6] | MARTIN D, YOHAI V J. Influence Functionals in Time Series[J]. The Annals of Statistics, 1986, 3(14):781-818. |
| [7] | LOUNI H. Outlier Detection in ARMA Models [J]. Journal of Time Series Analysis, 2005, 6(29): 1057-1065. |
| [8] | MCCULLOCH R E, TSAY R S. Bayesian Analysis of Autoregressive Time Series via the Gibbs Sample[J]. Journal of Time Series Analysis, 1992, 2(15): 235-250. |
| [9] | GUI Qingming, LI Tao, HENG Guanghui. Bayesian Method for Time Series Outliers Detection and Applications in Ionospheric VTEC Data Processing[J]. Geomatics and Information Science of Wuhan University, 2011, 36(7):802-806.(归庆明,李涛,衡广辉.时间序列异常值探测的Bayes方法及其在电离层VTEC数据处理中的应用[J].武汉大学学报:信息科学版, 2011, 36(7):802-806.) |
| [10] | LI Tao, HENG Guanghui, GUI Qingming.The Application of Bayesian Method in Autoregressive Model Outliers Detecting of Satellite Clock Error Prediction[J].CNSS World of China, 2010,35(4):15-20.(李涛,衡广辉,归庆明.AR序列异常值探测的Bayes方法在卫星钟差预报中的应用[J].全球定位系统, 2010, 35(4):15-20.) |
| [11] | GUI Qingming, GONG Yisong, LI Guozhong, et al. Bayesian Method for Detection of Gross Errors [J]. Acta Geodaetica et Cartographic Sinica, 2006, 35(4):303-307.(归庆明,宫轶松,李国重,等.粗差探测的Bayes方法[J].测绘学报, 2006, 35(4): 303-307.) |
| [12] | GUI Q, GONG Y,LI G, et al. A Bayesian Approach to the Detection of Gross Errors Based on Posterior Probability[J]. Journal of Geodesy, 2007, 81:651-659. |
| [13] | LI Xinna, GUI Qingming, XU Apei. Bayesian Method for Detection of Gross Errors Based on Classification Variables[J]. Acta Geodaetica et Cartographica Sinica,2008,37(3):355-360.(李新娜,归庆明,许阿裴.基于识别变量的粗差探测Bayes方法[J].测绘学报, 2008, 37(3):355-360.) |
| [14] | GUI Q, LI X, GONG Y, et al. A Bayesian Unmasking Method for Locating Multiple Gross Errors Based on Posterior Probabilities of Classification Variables[J]. Journal of Geodesy, 2011, 85:191-203. |
| [15] | CHRISTIAN P R. Monte Carlo Statistical Methods [M]. Berlin:Springer , 2004. |
| [16] | KOCH K R. Bayesian Inference with Geodetic Applications [M]. Berlin:Springer , 1990. |
| [17] | WANG Zhenlong, HU Yonghong. The Application of Time Series Analysis[M] .Beijing:Science Press,2007.(王振龙,胡永宏.应用时间序列分析[M].北京:科学出版社,2007.) |