2. 武汉大学 测绘遥感信息工程国家重点实验室,湖北 武汉 430079;
3. 云南省地图院,云南 昆明 650034
2.State Key Laboratory of Information Engineering in Surveying, Mapping and Remote Sensing, Wuhan University, Wuhan 430079, China;
3.Yunnan Provincial Mapping Institute, Kunming 650034, China
1 引 言
等高线树是用树结构来表达等高线层次结构的一种方式,其对等高线具有非常要的意义。首先,等高线树是表达等高线空间关系最合理和最有效的手段。对此,文献[1,2,3,4,5,6]进行了大量研究。其次,等高线树构建过程是对无序等高线集群有序化、组织化和结构化的过程,有利于等高线的遍历,提高等高线处理的效率和自动化程度。第三,构建等高线树是等高线结构化综合[7]的体现,等高线树充分表达了等高线组所隐含的空间关系,使等高线在结构化综合时能充分考虑等高线自身的空间信息以及其与周围等高线的关系。
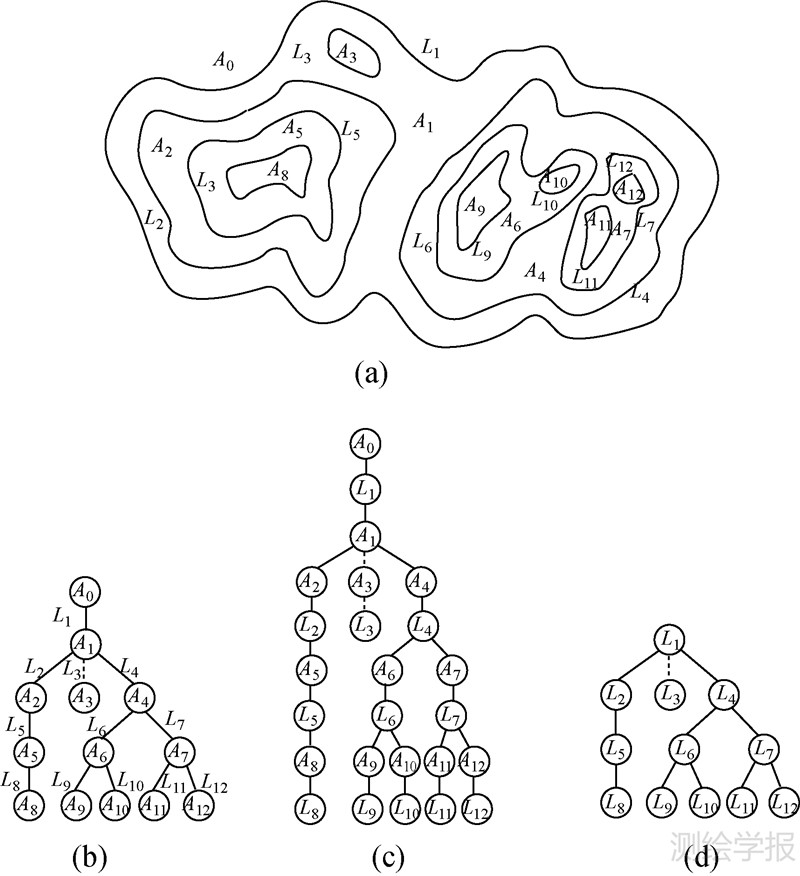
等高线树根据其节点以及边所代表含义的不同可有3种表示方法。如图 1所示,图 1(a)为一组等高线;图 1(b)中等高线树以等高线所包含的内部区域作为树的节点,等高线作为连接节点的边;图 1(c)中等高线树以等高线及其内部区域一起作为节点;图 1(d)中等高线树则以等高线作为树的节点,闭合等高线的包含关系作为连接节点的边。第3种等高线树显式地表达了等高线的包含及相邻关系,且数据结构比较简单,在3种模型中比较常用。本文即是采用此等高线树模型来表达等高线的空间关系。
在以往的研究中,文献[9]利用等高线包含关系,生成一种等高线包含树的数据结构,再将包含树转换成等高线树。该方法的实现需要一个前提,即等高线自我闭合或与边界闭合。但是在实际地形图中被图廓截断的等高线比比皆是,不解决这个问题很难实现等高线树的自动生成。针对被截断等高线的闭合问题,文献[6]把等高线图形分成封闭图形、贴边图形和开放图形3类,然后对这3类图形分别进行分析和处理。这为解决等高线的闭合问题提供了新的思路,但是最后没有描述出一个清晰的等高线树结构,只是获得了父节点与子节点间模糊的对应关系,并没有明确指出某一个父节点所对应的具体子节点。文献[10]从目标等高线与其相邻等高线的高程关系入手判断目标等高线的走向,以此作为目标等高线的闭合方向。然后通过生成贴边图形和开放图形在闭合方向上寻找与目标等高线相匹配的等高线,将之与图廓进行闭合。该方法充分利用了等高线的走向与高程变化方向的关系来判断目标等高线的前进方向。受该方法的启发本文提出了一种将截断等高线的各段统一成一条等高线的方法。此外,文献[11,12]通过研究等高线CDT(约束Delaunay 三角网)来获得等高线的层次结构。该方法绕过了闭合被截断等高线的问题,也成功地建立了等高线的层次结构,但是其建立的等高线层次结构比较松散,并非严格意义上的层次树结构。
本文在前人研究的基础上,提出一种新的等高线树生成算法——基于等高线CDT的等高线树生长法。主要研究基于CDT的等高线树生成方法,等高线CDT的构建方法参见文献[13,14,15,16]。
2 等高线关系的确定等高线关系包括比邻关系和包含关系。文献[17]通过等高线的Voronoi图来定义等高线的比邻关系,本文则利用CDT确定等高线的比邻关系。
下面以图 1(a)中等高线组为例说明上述关系。等高线可看做由线Li及Li所包含的区域Ai构成。
2.1 利用CDT确定等高线比邻关系等高线的比邻关系可描述为:
如果存在Ai∩Aj≠φ且Ai∧Aj= Ln(n=i或j),则等高线Li与等高线Lj比邻,记为N(Li,Lj)=1,如果等高线Li与等高线Lj不比邻则记为N(Li,Lj)=0;其中,Ai表示等高线Li的区域,Aj表示等高线Lj的区域,运算符“∩”表示两个区域求交,“∧”表示求两个区域的邻接线(连接线或分割线)。
本文利用构建等高线CDT来查找邻接等高线对。CDT是计算几何的一种几何构造,在空间剖分中,其三角形单元具有外接圆规则以及最小角最大规则。这一性质使其成为空间邻域分析的有力工具,被广泛用于地图综合、邻近关系处理中[18]。等高线CDT三角形边直接表达了等高线的邻近关系。图 2所示为等高线CDT的截图。通过分析三角形P1P2P3的边P1P3或P2P3很容易获知等高线L1和L2为比邻等高线。比邻的两根等高线可以通过其高程值的大小来确定其包含关系。
|
| 图 2 等高线CDT Fig. 2 Delaunay triangulation of contour |
等高线的包含关系体现在两个方面:
一是空间位置的包含,理想状态下表现为闭合等高线的嵌套包含,可归结为面状要素包含关系的判断,其定义可描述为如果Ai∩Aj≠Φ,则等高线称Li与Lj具有包含关系;更进一步,如果Ai∩Aj=Aj,则称Li包含Lj,反之如果Ai∩Aj=Ai,则称Lj包含Li。
二是高程值(相差一个等高距或相等)的包含,对于正向地貌表现为高程值低的等高线包含高程值高的等高线,对于负向地貌表现为高程值高的等高线包含高程值低的等高线。在查明了等高线的高程之后,高程值包含关系的判断便可归结为等高线比邻关系的判断。根据上述两个方面可以形成构建等高线树的不同思路,本文利用高程值来确定等高线包含关系。
对于已知具有比邻关系的两条等高线,其高程值关系具有以下规则:
(1) 两条比邻等高线的高程有三种关系:H(Li) > H(Lj)、H(Li) < H(Lj)、H(Li)=H(Lj),其中H(Li)表示等高线Li的高层值。
(2) 对于正向地貌来说,如果H(Li) > H(Lj),则等高线Lj包含等高线Li,Lj是Li的父亲节点;如果H(Li) < H(Lj),则等高线Li包含等高线Lj,Li是Lj的父亲节点;如果H(Li)=H(Lj),则Li与Lj为兄弟关系。而负向地貌正好与之相反。
基于上述规则,任取两条比邻等高线作为初始等高线对,分析其高程关系,可以建立一棵只包含两条等高线的初始树,称之为“树苗”。再通过查找初始树中所有节点的所有比邻等高线,分析其高程关系,并插入到相应的位子,得到一棵长出枝杈的小树。然后再对小树的根节点及所有叶节点进行比邻等高线的查找和高程关系的分析操作,以此递归直到叶节点和根节点等高线无比邻等高线为止。这一过程相当于一棵树从树苗逐渐成长的过程,本文称之为等高线树生长法。
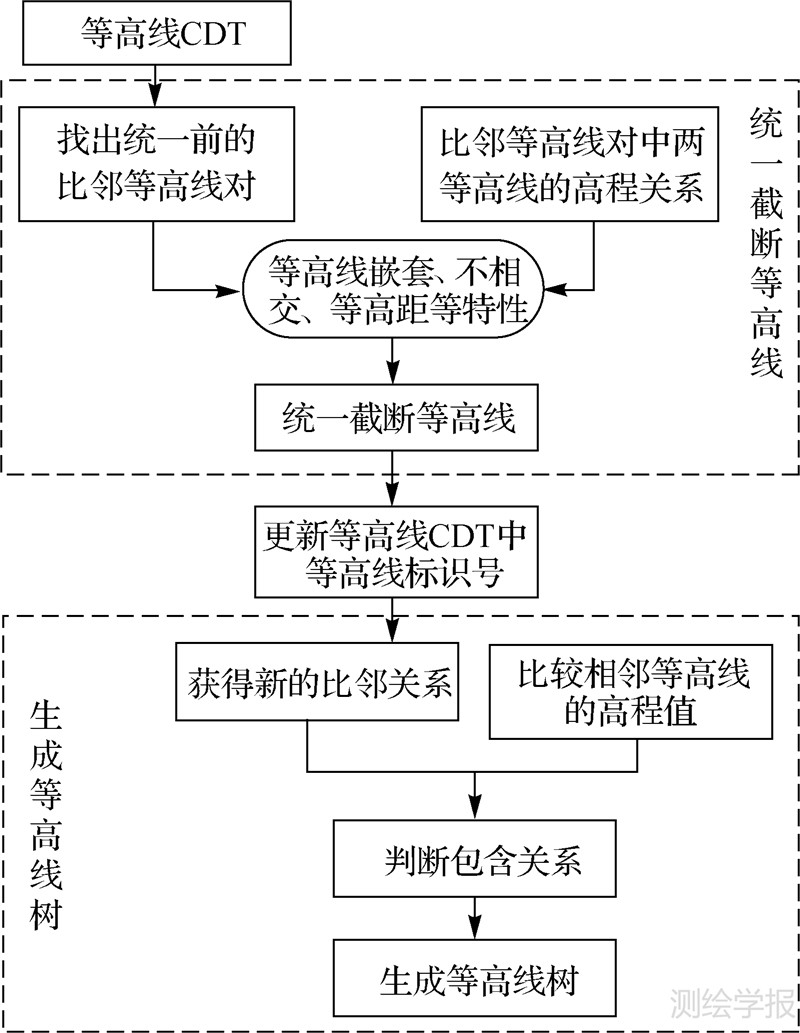
3 基于Delaunay三角网的等高线树生长算法 3.1 总体思路图 3为该方法的总体思路示意图。该方法首先对等高线构建约束Delaunay三角网,在此基础上查找等高线的比邻关系和高程关系,对被截断等高线的各段进行识别、判断,最后统一成一条等高线,并调整统一后的等高线标识(ID)。然后对统一后的等高线利用CDT再次查找等高线的比邻关系和高程关系,实现等高线树的生成。
|
| 图 3 总体思路示意图 Fig. 3 Schematic diagram of the general idea |
根据等高线的嵌套性质,利用等高线的比邻关系和高程关系判断出原本属于同一条等高线的非闭合等高线,并在逻辑上进行统一(在实际地图显示中它们还是断开的)。对于正向地貌而言,从嵌套的内层到外层高程值成等差递减,差值为一个等高距(负向地貌与之相反)。对于正向地貌可以利用等高线这种层层嵌套的性质,从高程最高的内部开始,逐层向外判断与之相邻的等高线,实现对断开的等高线进行识别和统一。
从高程最大的“山头”等高线开始,依次向外查找与其相邻的所有等高线,将相邻等高线中高程相同的等高线作为待判别的目标等高线集。再向外查找目标等高线集中所有等高线的相邻等高线,作为辅助等高线集。等高线统一的过程可分为3种情况:
(1) 如果辅助等高线集包含高程值低于目标等高线集中等高线的等高线,则将目标等高线集中的等高线视为同一根等高线,并将辅助等高线集作为新的目标等高线集直到辅助等高线集为空。
(2) 如果辅助等高线集中包含高程值与目标等高线集中高程值相等的等高线,则重新找另一个高程次高或相同(比之前一个山头)的“山头”等高线作为新的起始等高线重复上述过程,直到所有的等高线都处理过。
(3) 如果辅助等高线集中包含等高线的高程值既有低于目标等高线集中等高线高程值的,亦有等于目标等高线集中等高线的,则将目标等高线集中的等高线视为同一根等高线。这时需将辅助等高线集按高程值分为两个子集,两个子集的高程值分别低于和等于目标等高线集。将前者直接作为新的目标等高线集,按情况(1)处理,后者按情况(2)处理。
图 4为一个具体的等高线统一过程示例。利用上述原理,从等高线1开始,找到一条比邻等高线2,不需统一;然后找到等高线2的比邻等高线3和4,利用上述原理将其统一标识为3;利用统一后的等高线3(包含原等高线3和4,其比邻等高线也包含原等高线3和4的比邻等高线)对等高线5和6进行统一,直到所有等高线处理完。

|
| 图 4被截断等高线的统一 Fig. 4 Identification of truncated contour |
下面以正向地貌为例说明等高线树生长法的具体实施步骤(图 5)。
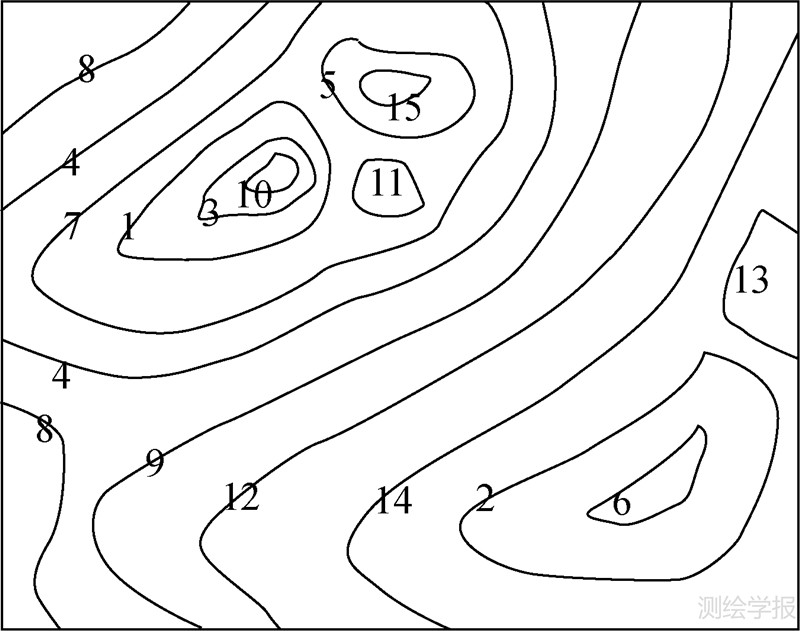
|
| 图 5 等高线图 Fig. 5Contour map |
(1) 利用等高线CDT找出比邻等高线对,记录下等高线对,将其ID号对存入映射表ID_Map中,表 1为图 6所示等高线的ID_Map表,其中每一行为一个等高线对包含的两条等高线ID号。查找比邻等高线需剔除平三角形(三角形的3个顶点都在同一条等高线上),注意在记录等高线对的过程中要剔除重复的对,因为两条等高线之间往往存在多个关联三角形。
| 等高线ID1 | 等高线ID2 |
| 1 | 3 |
| 2 | 13 |
| 3 | 10 |
| 4 | 7 |
| 4 | 9 |
| 5 | 15 |
| 5 | 11 |
| 6 | 2 |
| 7 | 1 |
| 8 | 9 |
| 8 | 4 |
| 9 | 12 |
| 11 | 7 |
| 12 | 14 |
| 13 | 14 |
| 14 | 2 |
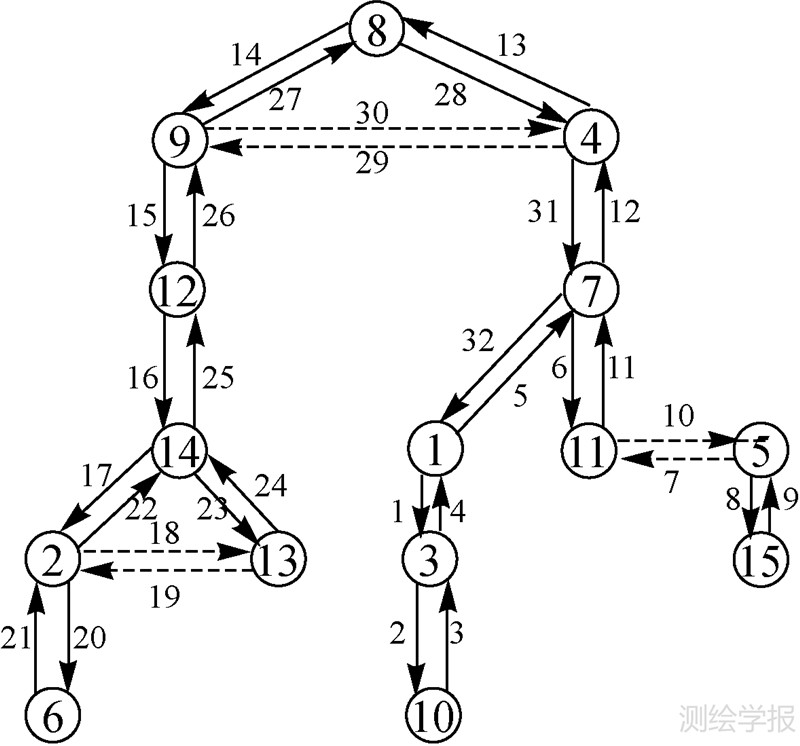
|
| 图 6 等高线树生成流程 Fig. 6 Process of contour tree generation |
(2) 将每条等高线的ID及其高程作为一个键值对存入映射表Elevation_Map中,表 2为图 5中等高线的高程表。
| 等高线ID1 | 高程H |
| 1 | 120 |
| 2 | 130 |
| 3 | 130 |
| 4 | 100 |
| 5 | 120 |
| 6 | 140 |
| 7 | 110 |
| 8 | 90 |
| 9 | 100 |
| 10 | 140 |
| 11 | 120 |
| 12 | 110 |
| 13 | 130 |
| 14 | 120 |
| 15 | 130 |
(3) 构建初始等高线树(C_Tree)。从ID_Map表中取出等高线对〈C1,C3〉,从Elevation_Map表中获取C1的高程H(C1),C3高程H(C3)。情况如下:
如果H(C1) > H(C3),将C3作为C_Tree的临时根节点,将C1作为C3的子节点插入到C3下面,获得初始等高线树。在ID_Map表中删除〈C1,C3〉对。
如果H(C1) < H(C3),则将C1作为C_Tree的临时根节点,将C3作为C1的子节点插入到C1下面,获得初始树。在ID_Map表中删除〈C1,C3〉。
如果H(C1)=H(C3),则将C1和C3作为兄弟节点,同时作为C_Tree的临时根节点,获得初始树。在ID_Map表中删除〈C1,C3〉。
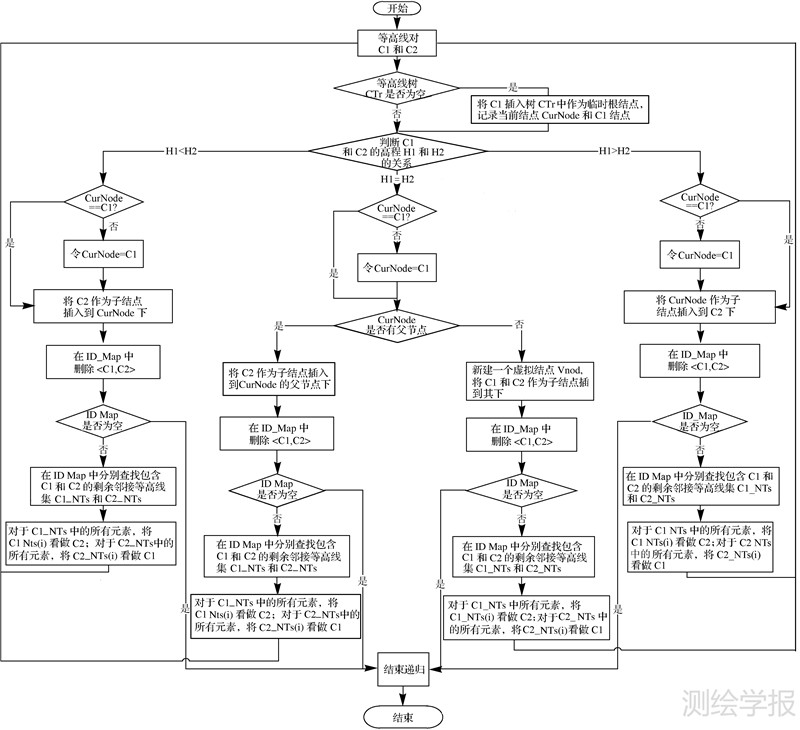
(4) 等高线树“生长”过程。递归搜索当前树中每个叶节点或树根的所有未处理的比邻等高线,构成邻接等高线集合。假设当前树中的一个叶节点(或根)为C,其邻接等高线集合NCs={Ci||N(C,Ci)=1,i=0,1,2,…,n}。依次根据H(C)和H(Ci)判断C和Ci的关系(是父子节点还是兄弟节点,判断依据和过程同第(3)步中生成初始树时相同),并将Ci插入到树中的相应位置。递归处理直到ID_Map表中没有未处理的等高线对。图 6为图 5中等高线利用生长法生成等高线树的过程图。图 7为上述递归处理的流程图。
|
| 图 7 递归流程图 Fig. 7 Flow chart of recursive process |
注意如果H(C)=H(Ci),Ci为C的兄弟节点,此时若C不为根节点,则将Ci插入C的父节点下;此时若C为根节点,由于一棵树只能包含一个根节点,出现这种情况时可以虚拟一个根节点N0,将C和Ci同时作为N0的子节点,或者直接将Ci作为C的一个子节点插入C下,并对Ci标记,注明其为C的兄弟节点。当C或Ci的父节点出现时再删除N0,或将Ci从C下提取出来放到它们共同的父节点下。
4 试 验在构建等高线树之前可以利用Douglas算法并设定一个较小的阈值对该组等高线进行化简,去掉多余点,以提高运算的效率。
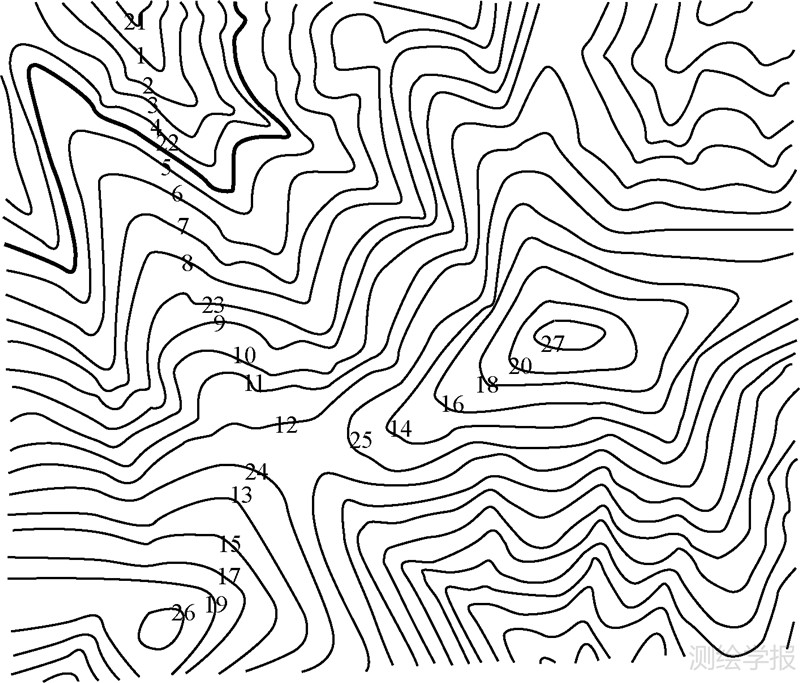
4.1 试验数据试验用等高线数据为某山区1∶5万等高线地形图上的一小块区域,等高距为20m,数据格式为shp格式(图 8)。所选区域包含两个山头,等高线形状复杂多样,且多为被图廓截断的等高线,具有一定的代表性和复杂性。
|
| 图 8 试验等高线组 Fig. 8 Contour group for experiment |
编程语言C++,平台为VC6.0,运行环境为Windows7系统。
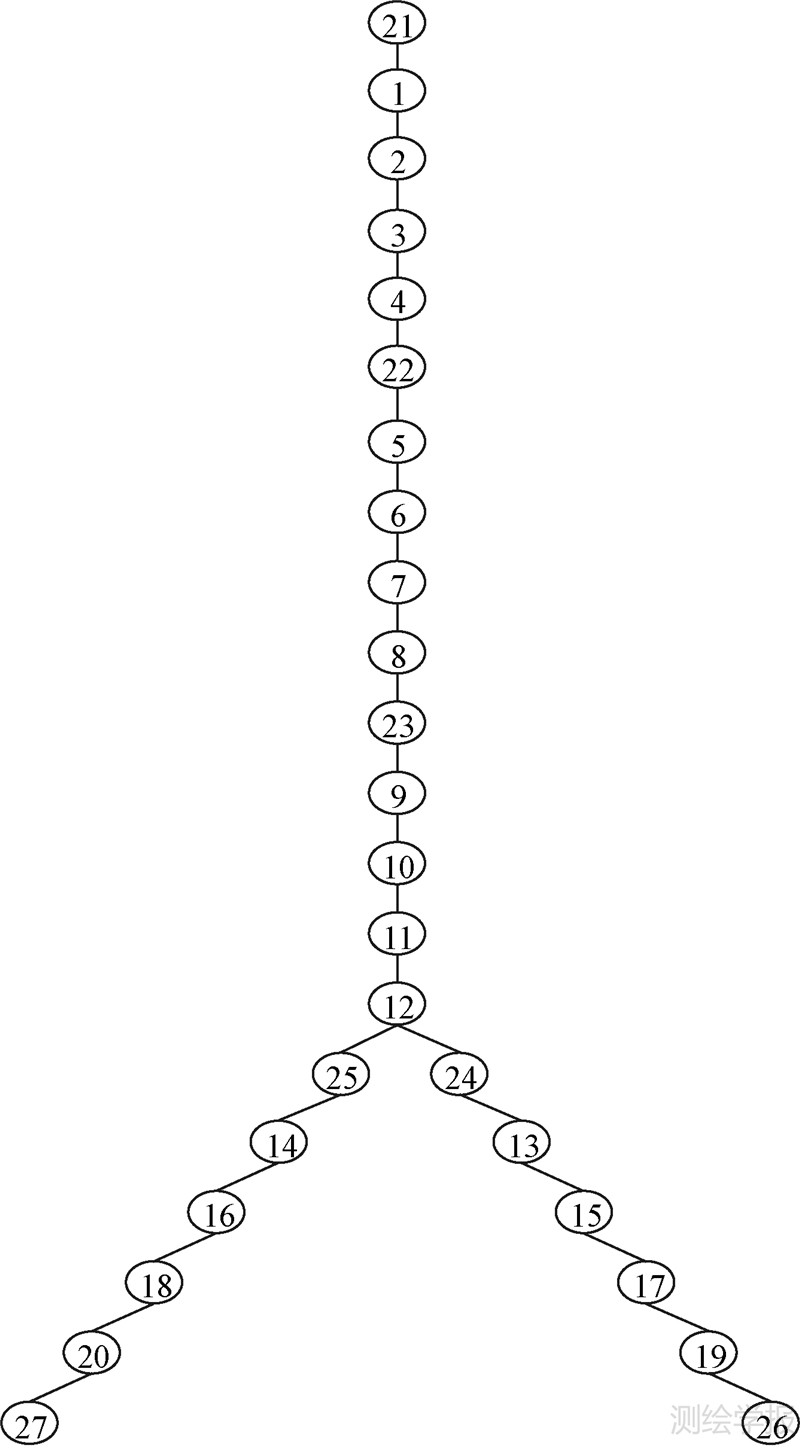
4.3 试验结果图 9是试验得到的等高线树分色显示,从父节点到子节点灰度逐渐变浅。图 10为相应的等高线树。

|
| 图 9 等高线树分色示意图 Fig. 9 Color diagram of contour tree |
|
| 图 10 等高线树 Fig. 10 Contour tree |
该方法对单向地貌地形图等高线生成等高线树的非常有效。对于一幅既有负向地貌,又有正向地貌的地形图生成等高线树时,本文采取的思路是,首先区分开正向地貌和负向地貌(一般的方法为统一等高线的走向,比如都为逆时针,则左高右低为正向地貌,右高左低为负向地貌),然后分别对正向地貌和负向地貌利用该方法生成等高线树。对正向地貌和负向地貌利用该方法生成等高线树的方法基本相同,只是其中父子关系的判断是相反的。
该算法时间复杂度与等高线条数n有关,根据表 1可知,在极限情况下表 1中有(n(n+1)/2)记录,而每条记录处理都可在常数c步内完成,所以,算法的时间复杂度为O(c(n+1)n/2),即O(n×n)。
基于CDT的等高线树生长算法在处理图幅范围较大的等高线图时效率有待提高,CDT的计算以及关联等高线对的查找消耗了大量的时间,在以后的研究中还有待优化和改善。
4.5 应 用本方法中统一被截断等高线的方法为等高线的闭合提供了一种新思路;利用本文方法生成的等高线树在等高线空间关系的表达、等高线结构的描述以及地貌结构化综合中都有重要意义。
5 结 论本文利用等高线CDT判明等高线的邻接关系和高程关系,在此基础上逻辑统一被截断的等高线并生成等高线树,最后通过一系列试验证明了该方法的可行性。该方法克服了闭合被截断等高线所带来的不便,可以直接对被截断等高线生成等高线树,为等高线空间关系的表达提供了重要手段,并且在等高线结构化综合中可以用来帮助地性线追踪。该算法能很好地对普通的等高线数据生成等高线树,对于一些特殊的情况,比如存在助曲线、陡坎、悬崖,以及等高线过河时,生成等高线树存在困难。
| [1] | QIAO Chaofei,ZHAO Renliang,CHEN Jun.Study of the Spatial Relations of Topographic Contour Lines[J].Geomatics and Spatial Geographic Information,2004,27(5):77-81.(乔朝飞,赵仁亮,陈军.等高线空间关系研究[J].测绘与空间地理信息,2004,27(5):77-81.) |
| [2] | QIAO Chaofei,CHEN Jun,LI Zhilin,et al.Representation of Spatial Relationships of Contours Based on Graph Theory[J].Journal of China University of Mining and Technology,2003,32(3):279-283.(乔朝飞,陈军,李志林,等.基于图论的等高线空间关系表达[J].中国矿业大学学报,2003,32(3):279-283.) |
| [3] | QIAO Chaofei,CHEN Jun,ZHAO Renliang,et al.Tree-based Representation and Computation of Spatial Relations of Topographic Contour Lines[J].Journal of China University of Mining and Technology,2005,34(5):570-573.(乔朝飞,陈军,赵仁亮,等.基于树的等高线空间关系表达与计算[J].中国矿业大学学报,2005,34(5):570-573.) |
| [4] | QIAO Chaofei,ZHAO Renliang,CHEN Jun,et al.A Voronoi Interior Adjacency-based Approach for Generating a Contour Tree[J].Geomatics and Information Science of Wuhan University,2005,30(9):801-804.(乔朝飞,赵仁亮,陈军,等.基于Voronoi内邻近的等高线树生成方法[J].武汉大学学:报信息科学版,2005,30(9):801-804.) |
| [5] | GUO Qingsheng,FEI Lifan.Tree-structure Model of Contour[J].Journal of Wuhan Teehnieal University of Surveying and Mapping,1993,18:44-46.(郭庆胜,费立凡.等高线的树结构模型[J].武汉测绘科技大学学报,1993,18:44-46.) |
| [6] | WU Hehai.The Research of Map Generalization Basic Theories and Technology[M].Beijing:Surveying and Mapping Press,2004:262-268.(毋河海.地图综合基础理论与技术方法研究[M].北京:测绘出版社,2004:262-268.) |
| [7] | WU Hehai.Structured Approach to Implementing Automatic Cartographic Generalization[J].Journal of Wuhan Technical University of Surveying and Mapping,1996,21(3):277-295.(毋河海.自动综合的结构化实现[J].武汉测绘科技大学学报,1996,21(3):277-295.) |
| [8] | LIU Ying.The Expression,Recognition and Generalization of Space Graphics[D].Zhengzhou:Information Engineering University,2005:100-102.(刘颖.空间图形的表达、识别与综合[D].郑州:信息工程大学,2005:100-102.) |
| [9] | WANG Yongming.An Algorithm for Automated Labeling and Checking Vector-based Contour Maps[J].Chinese Journal of Computers,2002,25(9):1-5.(王永明.一种基于矢量方法的等高线自动标定与检验算法[J].计算机学报,2002,25(9):1-5.) |
| [10] | ZHANG Linlin.The Research of Structured Method of Geomorphology's Automated Generalization[D].Zhengzhou:Information Engineering University,2005.(张琳琳.地貌自动综合的结构化方法研究[D].郑州:信息工程大学,2005.) |
| [11] | AI Tinghua,GUO Renzhong,LIU Yaolin.A Binary Tree Representation of Curve Hierarchical Structure in Depth[J].Acta Geodaetica et Cartographica Sinica,2001,30(4):343-348.(艾廷华,郭仁忠,刘耀林.曲线弯曲深度层次结构的二叉树表达[J].测绘学报,2001,30(4):343-348.) |
| [12] | ZHENG Chunyan,GUO Qingsheng,HU Huake,et al.Method for Constructing the Hierarchical Structure of Contour Lines Based on Constrained Delaunay Triangulation[J].Geomatics and Information Science of Wuhan University,2008,33(5):524-527.(郑春燕,郭庆胜,胡华科,等.基于约束Delaunay三角网建立等高线层次结构的方法[J].武汉大学学报:信息科学版,2008,33(5):524-527.) |
| [13] | LIU Hehui,LUO Yongjun.Speedy Constructing and Processing TIN Based on Contours[J].Engineering of Surveying and Mapping,2009,18(2):55-58.(刘合辉,罗勇军.基于等高线三角网快速构建与处理[J].测绘工程,2009,18(2):55-58.) |
| [14] | REN Zhenna,LI Binbing,ZHOU Hao,et al.Research and Realization of Delaunay Triangulation Algorithm Based on Contour Lines[J].Journal of Engineering Graphics,2006,27(6):54-58.(任振娜,李斌兵,周浩,等.应用等高线构建Delaunay三角网算法的研究与实现[J].工程图学学报,2006,27(6):54-58.) |
| [15] | REN Zhenna,YANG Ying.Algorithm Study of the Constrained Delaunay Triangulation Using Once for All Generation[C]//Proceedings of the Second National Conference on Geometric Design and Computing.Hefei:CSIAM,2005:151-154.(任振娜,杨颖.一次性生成约束Delaunay三角网的算法研究[C]//第二届全国几何设计与计算学术会议论文集.合肥:中国工业与应用数学学会几何设计与计算专业委员会,2005:151-154.) |
| [16] | WANG Tao,WU Hehai.Construction and Applications of Topological Relation among Contour Lines[J].Geomatics and Information Science of Wuhan University,2004,29(5):438-442.(王涛,毋河海.等高线拓扑关系的构建以及应用[J].武汉大学学报:信息科学版,2004,29(5):438-442.) |
| [17] | LIU Jianjun,CHEN Jun,WANG Donghua,et al.The Study of Description and Application of Contour Adjacency Relationship[J].Acta Geodaetica et Cartographica Sinica,2004,33(2):174-178.(刘建军,陈军,王东华,等.等高线邻接关系的表达及应用研究[J].测绘学报,2004,33(2):174-178.) |
| [18] | AI Tinghua,ZHU Guorui,ZHANG Genshou.Extraction of Landform Features and Organization of Valley Tree Structure Based on Delaunay Triangulation Model[J].Journal of Remote Sensing,2003,7(4):292-297.(艾廷华,祝国瑞,张根寿.基于Delaunay三角网模型的等高线地形特征提取及谷地树结构化组织[J].遥感学报,2003,7(4):292-297.) |


