2. 大连舰艇学院 海洋测绘工程军队重点实验室,辽宁 大连 116018;
3. 海军出版社,天津 300450
2. Key Laboratory of Hydrographic Surveying and Mapping of PLA, Dalian Naval Academy, Dalian 116018,China;
3. Navy Press, Tianjin 300450,China
1 引 言
高质量的数字水深模型(digital depth model,DDM)构建,在海上航行、海洋资源开发、海洋工程建设、海战场环境建设和海洋科学研究等应用领域都具有重要意义[1]。随着多波束全覆盖水深测量技术的应用,水深数据量陡然增加,如何利用海量多波束水深数据,进行高精度的数字水深建模,已引起国内外学者广泛关注。文献[2, 3, 4]采用网格插值方法,构建基于多波束水深数据的海底地形模型。然而,目前使用的这些网格DDM构建方法,基本上按照相同的网格大小(或间距)来内插水深。这种等间隔的内插方法,可能在一些平坦海区造成水深数据量过大,在一些复杂海区水深数据密度不够,无法根据不同海区水深变化情况和内插质量要求作出灵活调整。近年来,针对陆地不同地形变化的实际情况,已有学者提出了自适应四叉树建模算法[5, 6]。这些算法都通过局部的地形描述量是否大于某一固定阈值来确定网格的自适应剖分,但没有深入分析这一固定阈值确定的理论依据,未给出能保证模型达到预期精度的阈值确定方法,造成建模过程中缺少有机、可靠的质量调控。笔者在深入分析影响DDM精度因素的基础上,借鉴DEM中地形复杂因子的相关思想[7],设计阈值确定的数学方法,构建顾及水深复杂度的自适应网格DDM,论证自适应网格在提高DDM质量上的潜能[8]。但是,这种方法需要在自适应构网前进行大量的比对试验和统计分析,建立DDM精度与水深复杂度、网格间距等影响因子间的函数关系。这一方面将导致自适应建模效率相对较低;另一方面,这种构建区域采用同一统计函数关系,仍难以准确反映局部区域的细节变化,限制了模型最终的自适应调节质量。
自2008年,国际海道测量组织在新版国际海道测量标准S-44(5th)中将不确定度概念引入海道测量数据处理后[9],文献[10]研究了原始观测水深的不确定度计算方法,文献[11]探索了水深不确定度在DDM内插的传播规律,挖掘其在数字水深建模中的潜力。用不确定度解决目前自适应网格DDM构建存在的上述不足,进一步提高水深自适应建模效率和质量,具有理论和现实意义。
2 基于区域平均垂直不确定度的自适应数字水深建模方法 2.1 区域平均垂直不确定度计算 2.1.1 网格区域DDM参数及区域顶点的不确定度计算
(1) 网格区域DDM参数计算
为避免“龙格”现象,通常将地表分解成一系列的局部区域,采用低阶多项式,来表达地形地貌[12]。借鉴上述思想,并考虑到双线性内插也可用于规则网格模型的手工作业,采用如式(1)所示的双线性多项式[1]作为局部网格区域水深建模的数学模型。
要在局部区域采用双线性多项式建立起区域水深模型,首先需根据一定量的已知数据点,计算式(1)中的模型参数λi(i=1,2,3,4),然后推求区域内任意一点水深值z,从而达到局部水深建模的目的。假设在局部区域i内(本文采用正方形网格区域),按照观测点的平面位置分布情况,均匀选取n(设n=16)个观测点,平面位置和水深观测值分别为(xij,yij)和zij(j=1,2,…,n),代入式(1),并建立相应的误差方程组Vi=BiXi-Li。
根据最小二乘原理,求出网格区域i的模型参数最优估计解
考虑到国际海道测量标准S-44(5th)开始用不确定度来代替传统的误差概念[9],而且用于建模的当前多波束水深数据都可得到不确定度信息[10, 11],故本文采用水深不确定度,计算和表达各离散点水深数据的不等精度性。参考文献[13],构造权阵Pi为
式中,UH,ij与 分别为网格区域i内离散点j的水平与垂直不确定度;sH为一个受水平不确定度影响的系数因子,通常取1.96;dmin为最小网格间距;α为幂指数,通常取2.0。
分别为网格区域i内离散点j的水平与垂直不确定度;sH为一个受水平不确定度影响的系数因子,通常取1.96;dmin为最小网格间距;α为幂指数,通常取2.0。
参考文献[10],计算多波束水深数据在水平和垂直方向上的标准不确定度uposition和udepth。
为与国际海道测量标准S-44(5th)中的表达一致[9],采用式(4)计算水深的水平和垂直扩展不确定度UH和UV(简称水深水平和垂直不确定度)来表示[10]
(2) 网格区域顶点的水深及其垂直不确定度的计算
利用式(2)求出网格区域i模型参数 后,根据四个顶点平面位置(自左下角顶点开始、按逆时针顺序),分别为(xij,yij),利用式(1)求出对应位置的水深最优估值
后,根据四个顶点平面位置(自左下角顶点开始、按逆时针顺序),分别为(xij,yij),利用式(1)求出对应位置的水深最优估值 ,即
,即
根据GUM方法[14],当z=f(λ1,λ2,λ3,λ4)时,则z的标准不确定度uz是由这4个参数的不确定度u(λj)以一定的传播规律联合构成,即
式中,z为函数值;λj为自变量;u(λj)为λj的标准不确定度(标准差);u(λj,λk)为λj、λk的协方差估计值。根据协方差传播律,得 中
中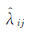 (j=1,2,3,4)的标准不确定度u(
(j=1,2,3,4)的标准不确定度u(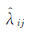 )与协方差估计值
)与协方差估计值
 中第j行、第k列的元素,模型单位权的标准不确定度ui0=
中第j行、第k列的元素,模型单位权的标准不确定度ui0= 。其中,对于网格i中选取的n个离散点(取n=16)的点j而言,其不确定度uij主要由两部分构成:一部分为原始水深测量引起的不确定度u′ij,另一部分为模型自身对水深变化的描述所引起的不确定度u″ij。
。其中,对于网格i中选取的n个离散点(取n=16)的点j而言,其不确定度uij主要由两部分构成:一部分为原始水深测量引起的不确定度u′ij,另一部分为模型自身对水深变化的描述所引起的不确定度u″ij。
基于GUM方法,计算网格区域i中顶点水深 垂直标准不确定度
垂直标准不确定度 ;基于协方差传播律,可计算网格区域i中顶点水深
;基于协方差传播律,可计算网格区域i中顶点水深 的协方差估计值。
的协方差估计值。
为与国际海道测量标准S-44(5th)中的表达一致,将垂直标准不确定度的 置信度扩展至95%,采用水深的垂直不确定度
置信度扩展至95%,采用水深的垂直不确定度 来表示,即
来表示,即 。
。
采用式(8)所示的网格双线性内插方法[11],计算网格区域i内任意一点p(xp,yp)的水深zp
式中 ,表示网格间距。
,表示网格间距。
针对式(8),基于GUM方法,来计算内插点p水深的垂直标准不确定度。
为与国际海道测量标准S-44(5th)中的表达一致,将垂直标准不确定度u(zp)的置信度扩展至95%,采用水深垂直不确定度U(zp)来表示,得:U(zp)=1.96u(zp)。
计算DDM在网格区域i内的平均垂直不确定度。经整理,得
式中,Ui(x,y)表示置信度95%下网格i内点(x,y)处水深z的垂直不确定度;Ωi表示网格区域i;Si表示该区域的面积,即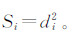 。
。
因此,根据式(5)~式(9),可计算网格i所构DDM的区域平均垂直不确定度。
2.2 基于区域平均垂直不确定度的自适应网格DDM 2.2.1 基于自适应四叉树的数据组织由式(9)计算的区域平均垂直不确定度主要由两方面原因形成的,一是由于观测误差引起的,二是由水深模型近似化描述引起的。随着测量仪器与技术的不断发展,尤其对多波束水深测量,水深观测引起的垂直不确定度通常要小于水深值的2%[15]。而在水深变化趋势不一致区域,由于目前规范所要求的水深间隔通常较大[16],水深模型近似化描述引起的区域垂直不确定度相对水深观测引起的垂直不确定度来说,已成为影响模型构建质量的主要因素,并可通过网格不断剖分的方法来削弱。
如图 1所示,对于网格区域A,利用式(1)~式(9),计算区域平均垂直不确定度,评估DDM在该区域的构建质量 ,并与预设质量指标Uexp相比较,判断当前网格是否需要剖分:若
,并与预设质量指标Uexp相比较,判断当前网格是否需要剖分:若 ,即用当前网格所构DDM质量不能满足预设指标,则将当前网格剖分为A1、A2、A3、A4 4块网格区域;若
,即用当前网格所构DDM质量不能满足预设指标,则将当前网格剖分为A1、A2、A3、A4 4块网格区域;若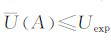 ,则不需继续剖分,选取该网格4个顶点作为自适应网格节点。当然,若当水深数据质量不佳、预设指标过高时,不管怎么剖分可能也无法达到建模质量要求,这时用观测数据点数不满足式(2)要求作为结束条件,并提示预设质量指标过高,只能放宽要求。采用自适应四叉树的数据结构[17],可有效地组织网格剖分中产生的这些网格节点。
,则不需继续剖分,选取该网格4个顶点作为自适应网格节点。当然,若当水深数据质量不佳、预设指标过高时,不管怎么剖分可能也无法达到建模质量要求,这时用观测数据点数不满足式(2)要求作为结束条件,并提示预设质量指标过高,只能放宽要求。采用自适应四叉树的数据结构[17],可有效地组织网格剖分中产生的这些网格节点。

|
| 图 1 基于自适应四叉树的数据组织 Fig. 1 Data organization based on adaptive quadtrees |
由于采用基于平均垂直不确定度的区域分块方式建模,两相邻网格区域采用不同的原始观测点数据来建模,在两网格的公共边界处,不同网格区域模型所得水深通常会存在差异(或不一致性)[17]。故需增加一定的约束条件,使得相邻网格区域的水深模型在公共边界处连续(或保持一致)。
如图 2所示,对于两相邻网格区域j和k,模型参数为Xj和Xk,其拼接处节点分别为M和N。增加式(10)中两个约束方程,可保证DDM在该相邻区域拼接处的空间连续性。
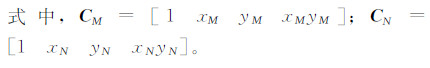

|
| 图 2 相邻网格区域拼接 Fig. 2 Jointing of adjacent areas |
3.1 模型质量分析
为了比较等间距规则网格DDM[2, 3](简称等间距法)、顾及水深复杂度的自适应网格DDM[8](简称水深复杂度法)与基于平均垂直不确定度的自适应网格DDM(简称不确定度法)的构建质量,使用CPU主频2.66 GHz、内存2 GB的计算机进行比对试验。在如图 3(a)所示的某多波束测深海区,采用高斯平面坐标表达地理范围为(3 306 550,41 418840)~(3 311 030,41 422 680),人工选取如图 3(b)所示的Ⅰ、Ⅱ、Ⅲ、Ⅳ、Ⅴ、Ⅵ 6块代表性区域,采用上述方法构建DDM。其中,区域Ⅰ的水深变化趋势基本一致;区域Ⅱ的水深变化不大但趋势多变;区域Ⅲ为包含Ⅰ、Ⅱ类型的混合区域;区域Ⅳ的水深变化幅度较大且趋势有变;区域Ⅴ为包含Ⅰ、Ⅳ类型的混合区域;区域Ⅵ为包含各类型的整体混合区域。

|
| 图 3 试验海区 Fig. 3 Experimental sea area |
均匀选取一定数量N的原始观测水深点作为检查点。设检查点i(i=1,2,…,N)的原始观测水深值为Z′i,而由DDM内插所得到的水深值为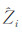 ,用式(11)来评价所建DDM的实际质量
,用式(11)来评价所建DDM的实际质量
由于水深复杂度法与不确定度法采用自适应调节的不等网格间隔机制,其网格节点个数难以与等间距法完全一致,故只能采用大致相当的水深数据量构建DDM并对其质量进行比对分析(表 1)。
| 区域 | 建模方法 | 网格节点数 | 实际质量/m2 |
| Ⅰ | 等间距法 | 9 | 0.02 |
| 水深复杂度法 | 9 | 0.02 | |
| 不确定度法 | 9 | 0.02 | |
| 等间距法 | 16 | 0.02 | |
| 水深复杂度法 | 16 | 0.02 | |
| 不确定度法 | 16 | 0.02 | |
| Ⅱ | 等间距法 | 289 | 0.41 |
| 水深复杂度法 | 289 | 0.62 | |
| 不确定度法 | 265 | 0.40 | |
| 等间距法 | 144 | 0.64 | |
| 水深复杂度法 | 147 | 1.00 | |
| 不确定度法 | 126 | 0.66 | |
| Ⅲ | 等间距法 | 374 | 0.38 |
| 水深复杂度法 | 378 | 0.32 | |
| 不确定度法 | 370 | 0.28 | |
| 等间距法 | 221 | 0.55 | |
| 水深复杂度法 | 238 | 0.43 | |
| 不确定度法 | 207 | 0.41 | |
| Ⅳ | 等间距法 | 153 | 0.26 |
| 水深复杂度法 | 126 | 0.45 | |
| 不确定度法 | 131 | 0.25 | |
| 等间距法 | 84 | 0.61 | |
| 水深复杂度法 | 83 | 0.93 | |
| 不确定度法 | 72 | 0.59 | |
| Ⅴ | 等间距法 | 324 | 0.34 |
| 水深复杂度法 | 323 | 0.21 | |
| 不确定度法 | 306 | 0.15 | |
| 等间距法 | 144 | 0.47 | |
| 水深复杂度法 | 145 | 0.41 | |
| 不确定度法 | 144 | 0.35 | |
| Ⅵ | 等间距法 | 525 | 0.64 |
| 水深复杂度法 | 546 | 0.55 | |
| 不确定度法 | 502 | 0.47 | |
| 等间距法 | 864 | 0.59 | |
| 水深复杂度法 | 886 | 0.38 | |
| 不确定度法 | 824 | 0.32 |
在水深变化趋势基本一致的区域(如区域Ⅰ所示),3种方法所构DDM的质量相同,这是由于这些区域的水深变化趋势单一且基本一致,自适应调节没有必要而且也起不到作用,导致建模中3种方法所采用的网格节点数相同。
在水深变化不大但变化趋势多变的区域(如区域Ⅱ所示)和水深变化幅度较大且趋势有变的区域(如区域Ⅳ所示),不确定度法比等间距法所构的DDM质量有较小程度的提高,以较少的网格节点达到较高的质量,而水深复杂度法所构DDM的质量反而有所下降,这是由于水深复杂度法建立的函数关系式是经统计分析得出的先验信息,很难完全适用于每一块网格区域,导致对个别复杂区域的网格剖分存在一定的不合理性,从而出现了相反的效果。
在各类混合区域(如区域Ⅲ、Ⅴ、Ⅵ所示),不确定度法构建的DDM质量最高,水深复杂法次之,等间距法最低。这是由于:① 等间距法只是简单地进行水深网格化处理,导致水深变化复杂区域的DDM质量相对降低,从而影响到最终构建的DDM质量;② 相比于等间距法,水深复杂度法与不确定度法能根据不同区域水深变化的实际情况,在变化复杂区域,缩小网格间距,加强水深细节表达,在变化平缓区域,适当增大网格间距,简化水深数据量,故可提高DDM的质量。相对于水深复杂度法,不确定度法所构建的DDM质量更高,这是由于不确定度法能更精细地计算局部区域的平均垂直不确定度,更有效地来进行水深数据的自适应组织和建模。
3.2 自适应调节质量分析为进一步对比分析不同方法的自适应建模性能,选取如图 3(b)所示Ⅰ、Ⅱ、Ⅲ、Ⅳ、Ⅴ、Ⅵ 6块典型区域。根据预先设置的DDM质量需求指标(以下简称预设指标,根据用户需求和规范要求设定),采用不同方法构建DDM。由于传统的等间距法只能根据人为定义和规范要求设定一固定的间距,进行模型构建,不具备根据预设质量指标自动确定模型间隔、并进行调节的能力,所以表 2中只对不确定度法和水深复杂度法的自适应调节质量进行分析。
| 区域 | 建模方法 | 预设指标 /m2 | 网格节 点数 | 实际质量 /m2 |
| Ⅰ | 水深复杂度法 | 0.04 | 9 | 0.02 |
| 不确定度法 | 9 | 0.02 | ||
| 水深复杂度法 | 0.09 | 9 | 0.02 | |
| 不确定度法 | 9 | 0.02 | ||
| Ⅱ | 水深复杂度法 | 0.49 | 495 | 0.36 |
| 不确定度法 | 265 | 0.40 | ||
| 水深复杂度法 | 1.00 | 215 | 0.66 | |
| 不确定度法 | 126 | 0.66 | ||
| Ⅲ | 水深复杂度法 | 0.49 | 238 | 0.43 |
| 不确定度法 | 207 | 0.41 | ||
| 水深复杂度法 | 0.81 | 169 | 0.58 | |
| 不确定度法 | 117 | 0.57 | ||
| Ⅳ | 水深复杂度法 | 0.36 | 180 | 0.35 |
| 不确定度法 | 131 | 0.25 | ||
| 水深复杂度法 | 0.64 | 126 | 0.45 | |
| 不确定度法 | 72 | 0.59 | ||
| Ⅴ | 水深复杂度法 | 0.36 | 323 | 0.21 |
| 不确定度法 | 198 | 0.21 | ||
| 水深复杂度法 | 0.81 | 145 | 0.41 | |
| 不确定度法 | 97 | 0.42 | ||
| Ⅵ | 水深复杂度法 | 0.64 | 546 | 0.57 |
| 不确定度法 | 502 | 0.47 | ||
| 水深复杂度法 | 1.00 | 285 | 0.97 | |
| 不确定度法 | 220 | 0.78 |
从表 2可以看出,水深复杂度法和不确定度法,都能根据预先设计的质量指标需求,自动确定网格剖分机制,实现水深模型的自适应构建。从几组能完成自适应建模情形中,两种方法建模实际检验质量均能基本达到预先设计的质量指标。应当说明的是,表 2中的试验都是针对最后的预先指标比较合适的情形。相对等间距法不能自动调控模型达到预设质量来说,两种方法在自动调控模型质量方面具有较大的优势。从区域Ⅰ的试验结果可以看出,对于水深变化平缓的区域,不确定度法与水深复杂度法的自适应调节能力基本相同。但从区域Ⅱ、Ⅲ、Ⅳ、Ⅴ、Ⅵ的试验结果可以看出,对于水深变化不一致区域而言,不确定度法与水深复杂度法相比,都能明显地通过更少的网格水深节点达到更高模型质量的目的,具有更强的自适应调控能力。这是由于水深复杂度法建立的函数关系式难以完全适用于每一块网格区域,从而导致个别区域的网格剖分存在一定的不合理性,而不确定度法能利用水深不确定度及其传递机制,更精细地计算局部区域的平均不确定度,进行水深数据的自适应组织和建模,故具有更强的自适应调节能力。
3.3 自适应调节效率分析为了进一步比较上述两种自适应调节方法在数字水深建模效率上的差异,利用上述原始水深数据来构建DDM。采用网格剖分依据确定与构网耗时两项指标,比较两种方法的建模效率,结果如表 3所示。其中,表 3中各区域试验的第1、2组分别与表 2中各区域的两组试验相对应。
| 10-2s | |||||||||||||
| 建模 方法 | 网格剖分依据确定 | 自适应构网耗时 | |||||||||||
| Ⅰ | Ⅱ | Ⅲ | Ⅳ | Ⅴ | Ⅵ | ||||||||
| 1 | 2 | 1 | 2 | 1 | 2 | 1 | 2 | 1 | 2 | 1 | 2 | ||
| 水深复 杂度法 | 需要比对试验,分析建立DDM 质量与影响因子的关系 | 139 | 139 | 28 | 26 | 84 | 82 | 16 | 16 | 148 | 144 | 9991 | 9720 |
| 不确定 度法 | 不需统计分析,利用区域平均垂 直不确定度直接确定 | 63 | 63 | 22 | 16 | 49 | 45 | 11 | 8 | 64 | 59 | 1280 | 1189 |
由表 3可以看出:① 水深复杂度法在构网前需进行大量的比对试验和统计分析,获取相关先验信息,来建立DDM质量与水深复杂度、网格间距等因素间的函数关系,而不确定度法可利用水深不确定度及其传播规律,直接计算DDM区域平均垂直不确定度,自动确定网格剖分层次;② 水深复杂度法需建立局部区域水深三角网,并根据各局部区域的水深复杂程度来确定剖分策略、进行水深数据组织,效率较低,不确定度法在自动确定网格部分层次的同时,进行水深自适应组织和建模,就算不计水深复杂度法的网格剖分依据确定时间,不确定度法效率仍明显优于水深复杂度法。
4 结 论通过分析、计算及试验比对,结论如下:
(1) 在水深变化趋势基本一致的区域,不确定度法相对于等间距法和水深复杂度法,用等量的点所构建的DDM质量没有明显的提高;在水深变化趋势不一致的区域,相对于等间距法与水深复杂度法来说,不确定度法对DDM质量均有一定程度提高。
(2) 相对于等间距法来说,不确定度法能根据网格区域的平均垂直不确定度,自动确定网格剖分层次和网格大小,控制模型质量达到预先设计的指标要求。相对于水深复杂度法来说,具有更强的自适应调控能力。
(3) 与水深复杂度法相比,不确定度法不需要通过统计分析来获取先验信息,可自动利用不确定度直接确定网格剖分层次,而且在自适应建模过程中所耗费的时间也明显减少。
当然,本文只对几种较为典型的水深变化情况进行比对分析。对于更详细的水深变化分类和水深范围分级,以及水深数据质量对建模质量更详细的影响规律,还有待于进一步研究。
| [1] | SMITH S. The Navigation Surface: a Multipurpose Bathymetric Database [D]. New Hampshire: University of New Hampshire, 2003. |
| [2] | GAO Jinyao, JIN Xianglong, WU Ziyin. Construction of Submarine DTM from Raw Multibeam Data [J]. Marine Science Bulletin, 2003, 22(1): 30-38. (高金耀, 金翔龙, 吴自银. 多波束数据的海底数字地形模型构建[J]. 海洋通报, 2003, 22(1): 30-38.) |
| [3] | JIA Juntao, ZHAI Jingsheng, MENG Chanyuan, et al. Construction and Visualization of Submarine DEM Based on Large Number of Multibeam Data [J]. Journal of Geomantics Science and Technology, 2008, 25(4): 255-259. (贾俊涛, 翟京生, 孟婵媛,等. 基于海量多波束数据的海底地形模型的构建与可视化[J]. 测绘科学技术学报, 2008, 25(4): 255-259.) |
| [4] | ARSENAULT R. Real Time 3D display of Hydrographic Data for QA and QC [C]//Proceedings of the 2001 U.S. Hydrographic Conference. Athens:[s.n.],2001. |
| [5] | HUAI Yongjian, HAO Chongyang, FAN Yangyu, et al. A View-dependent Multi-resolution Terrain Simplification Based on Adaptive Quadtrees [J]. Journal of System Simulation, 2002, 14(6): 748-751. (淮永建, 郝重阳, 范养余,等. 基于自适应四叉树视相关的多分辨率地形简化[J]. 系统仿真学报, 2002, 14(6): 748-751.) |
| [6] | ZHANG Xiaohu, SHAO Yongshe, YE Qin. New LOD Method Based on Adaptive Quad-Tree for Terrain Visualization [J]. Journal of Computer Applications, 2009, 29(9): 2596-2598. (张小虎, 邵永社, 叶勤. 基于自适应四叉树的地形LOD算法[J]. 计算机应用, 2009, 29(9): 2596-2598.) |
| [7] | LIU Chun, SUN Weiwei, WU Hangbin. Terrain Complexity Factor and Its Relationship with Accuracy of DEM Terrain Representation [J]. Geomatics and Information Science of Wuhan University, 2009, 34(9): 1014-1019. (刘春, 孙伟伟, 吴杭彬. DEM地形复杂因子的确定及与地形描述精度的关系[J]. 武汉大学学报:信息科学版, 2009, 34(9): 1014-1019.) |
| [8] | JIA Shuaidong, ZHANG Lihua, CAO Hongbo, et al. A Method for Constructing Adaptive Grid Digital Depth Model Considering Depth Complexity [J]. Hydrographic Surveying and Charting, 2011, 31(2): 4-7. (贾帅东, 张立华, 曹鸿博,等. 顾及水深复杂度的自适应网格DDM构建方法[J]. 海洋测绘, 2011, 31(2): 4-7.) |
| [9] | IHO.S-44 IHO Standards for Hydrographic Surveys [S]. 5th ed. Monaco: International Hydrographic Bureau, 2008. |
| [10] | WU Chao, YIN Xiaodong, ZHANG Lihua, et al. The Method of Quality Estimation in Multibeam Sounding Data Based on Uncertainty [J]. Hydrographic Surveying and Charting, 2009, 29(3): 11-15. (吴超, 殷晓冬, 张立华,等. 基于不确定度的多波束测深数据质量评估方法[J]. 海洋测绘, 2009,29(3): 11-15.) |
| [11] | ZHANG Lihua, JIA Shuaidong, WU Chao, et al. A Method for Interpolating Digital Depth Model Considering Uncertainty [J]. Acta Geodaetica et Cartographica Sinica, 2011, 40(3): 359-365. (张立华, 贾帅东, 吴超,等. 顾及不确定度的数字水深模型内插方法[J]. 测绘学报, 2011, 40(3): 359-365.) |
| [12] | LI Zhilin, ZHU Qing. Digital Elevation Model [M]. Wuhan: Wuhan University Press, 2003. (李志林, 朱庆. 数字高程模型[M]. 武汉: 武汉大学出版社, 2003.) |
| [13] | CALDER B R. Automatic Processing of High-Rate, High-Density Multibeam Echosounder Data[J].Geochemistry,Geophysics,Geosystems, 2003,4(6):1-22. |
| [14] | BIPM, IEC, IFCC, et al. Guide of the Expression of Uncertainty in Measurement [S]. Switzerland: ISO, 1995. |
| [15] | LIU Yanchun, XIAO Fumin, BAO Jingyang, et al. Introduction to Hydrogrophy [M]. Beijing: Surveying and Mapping Press, 2006. (刘雁春, 肖付民, 暴景阳,等. 海道测量学概论[M]. 北京: 测绘出版社, 2006.) |
| [16] | Naval Institute of Hydrographic Surveying and Charting. GB12327-1998 Specifications for Hydrographic Survey [S]. Beijing: Chinese Standard Press, 1999. (海军海洋测绘研究所.GB12327-1998 海道测量规范[S]. 北京: 中国标准出版社, 1999.) |
| [17] | ZHANG L, YANG C, LIU D, et al. A Web-mapping System for Real-time Visualization of the Global Terrain [J]. Computers and Geosciences, 2005, 31(3): 343-252. |













