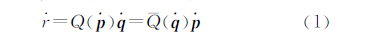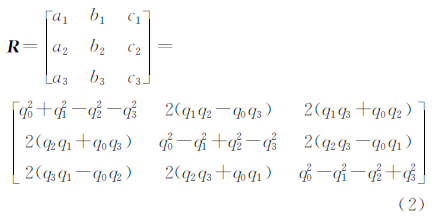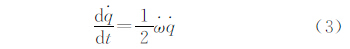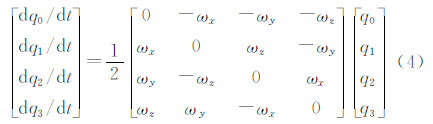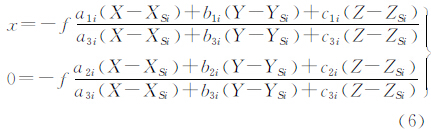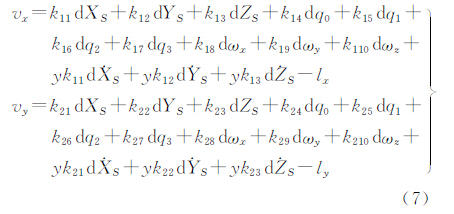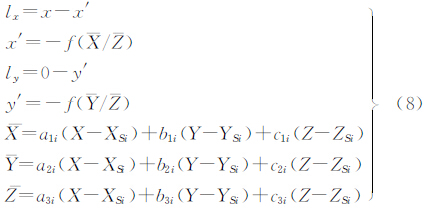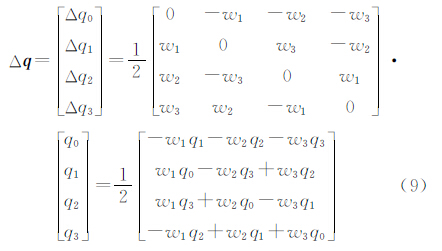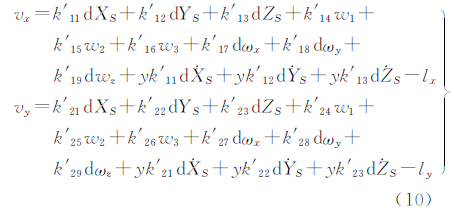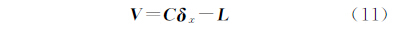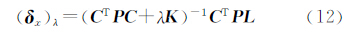1 引 言
影像外方位元素求解是高分辨率卫星遥感影像几何处理的一个基础性问题,是有效确定物像关系的关键,是利用卫星影像测制各种比例尺地形图的基本保障,一直以来都是国内外研究的热点。基于共线方程的严格几何模型由于求解精度高,几何意义明确,一直是外方位元素求解的首选[1]。国内外很多学者对此进行研究,构建很多实用的模型,如Kratky模型[2]、Westin模型[3]、动态轨道参数模型[4]、Toutin模型[5]、Poli模型[6]和Weser模型[7, 8]等。在上述所有的成像模型中,影像的成像姿态均是采用欧拉角进行描述,对线阵推扫卫星而言,卫星轨道高、传感器焦距长、摄影光束窄、视场角小、地面点存在的空间面等特点导致其影像定向参数之间存在很强的相关性,从而影响了外方位元素解算的稳定性,甚至迭代不收敛。同时由于欧拉角的周期性极易出现表达的奇异性和姿态插值不连续等问题。为解决利用欧拉角描述影像姿态可能出现的问题,本文采用四元数描述成像姿态。
四元数可以非常方便地表示空间三维旋转,并能有效避免采用欧拉角描述姿态可能引起的奇异性,具有线性程度高、计算时间少、计算误差小等特点,在机器人技术、计算机视觉、卫星姿态控制等领域得到广泛地应用。四元数也广泛应用在摄影测量中,为提高空三加密的数值稳定性和计算效率,文献[9]在处理ADS40影像的软件ORIMA中采用了四元数算法,将四元数用于实用化摄影测量处理软件中;文献[10]提出一种利用单位四元数实现无初值依赖的空间后方交会算法,试验表明该算法对外方位元素的初值不依赖;随后文献[11]提出一种类似摄影测量角锥体法的四元数空间后方交会算法,该算法需要首先迭代解算出摄站到控制点的距离,再获得四元数解析值;文献[12]在GPS/IMU辅助机载线阵CCD影像处理中,设计了基于单位四元数的IMU偏心角模型,将四元数球面线性插值(spherical linear interpolation,SLERP)引入到三线阵影像的定向片光束法平差中,并进行对比试验;文献[13]也将四元数SLERP引入到高分辨率卫星CCD影像的外定向中,结合单位四元数模为1的限制条件进行带约束条件的间接平差求解,试验结果表明该方法可行,然而未知数个数却增加到14个;文献[14]利用四元数描述进行线阵CCD影像的空间后方交会,使得未知数变为13个,至少需要7个控制点才能进行求解。这些成果的取得一方面体现四元数在线阵CCD影像处理中的可行,另一方面也表明利用四元数将增加未知数个数,可能引起定向元素的更加相关,从而增加地面控制点的数目,特别是增加约束条件进行求解时,会使方程出现病态、不稳定。
本文试图改善利用四元数使未知数个数增多的情况。因此,结合四元数在处理线阵影像上的优势,通过对高分辨率卫星遥感影像成像机理进行分析,采用四元数微分方程构建了严格的成像几何模型,以进行外方位元素的稳定求解,求解过程中引入独立的解算参数,使得方程求解不直接求解四元数,确保了未知数个数与现有方法相同,最后通过试验验证了本文方法和模型的合理性。
2 四元数微分方程四元数是一种形如 =q0+q1 i +q2 j +q3k的超复数,其中q0、q1、q2、q3为任意的实数,i、j、k为满足i2=j2=k2=-1,jk=-kj=i,ki=-ik=j,ij=-ji=k的虚数单位。在上述四元数的代数表达式中,q0为
=q0+q1 i +q2 j +q3k的超复数,其中q0、q1、q2、q3为任意的实数,i、j、k为满足i2=j2=k2=-1,jk=-kj=i,ki=-ik=j,ij=-ji=k的虚数单位。在上述四元数的代数表达式中,q0为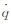 的实部,记为Re(
的实部,记为Re(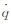 ),q1 i +q2 j +q3 k 为
),q1 i +q2 j +q3 k 为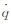 的虚部,记为Im(
的虚部,记为Im( 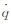 )。若Im(
)。若Im( 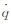 )=0,则四元数
)=0,则四元数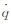 称为纯虚四元数。
称为纯虚四元数。
四元数有自己的运算法则,设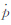 =P0+P1 i +P2 j +P3k=p0+p 为另一个四元数,则四元数
=P0+P1 i +P2 j +P3k=p0+p 为另一个四元数,则四元数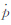 与
与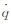 的乘积为
的乘积为
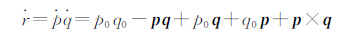
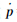 =[p0 p1 p2 p3]T,
=[p0 p1 p2 p3]T,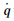 =[q0 q1 q2 q3]T和
=[q0 q1 q2 q3]T和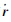 =[r0 r1 r2 r3]T,可将四元数的乘积写为矩阵形式
式中
=[r0 r1 r2 r3]T,可将四元数的乘积写为矩阵形式
式中
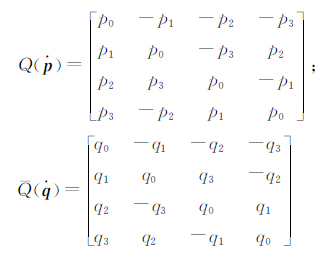
四元数很适合描述两个坐标系之间的旋转,给定一个四元数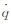 ,与之对应的旋转矩阵为 R ,则二者之间的关系如式(2)所示
,与之对应的旋转矩阵为 R ,则二者之间的关系如式(2)所示
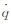 为描述坐标系旋转的四元数,d
为描述坐标系旋转的四元数,d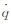 /dt为四元数
/dt为四元数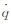 的一阶微分,设
的一阶微分,设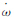 =0+ωxi+ωy j +ωzk,
=0+ωxi+ωy j +ωzk,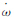 为一个坐标系相对于另一个坐标系的旋转角速度所对应的四元数。
为一个坐标系相对于另一个坐标系的旋转角速度所对应的四元数。
利用前面的四元数乘法规则,将上式写为矩阵形式,可得
四元数微分方程是四元数代数中很重要的一部分,在惯性导航、航天器姿态控制、机器人控制中具有重要应用,本文将其应用于高分辨率卫星遥感影像的外方位元素求解中。
3 基于四元数微分方程的外方位元素解算 3.1 基于四元数微分方程的成像几何模型高分辨率卫星遥感影像CCD传感器采用推扫成像,其影像的每一扫描行与被摄物体之间具有严密的中心投影关系,但平台的运动和姿态变化导致了各扫描行上的外方位元素各不相同。因此构建高分辨率卫星遥感影像成像几何模型的关键是建立各扫描行外方位元素之间的数学关系。考虑到卫星平台的飞行是按照一定的轨道且相邻两扫描行影像的成像间隔非常短,因此通常采用的方法是将外方位元素用随时间变化的多项式等数学模型来描述。
设扫描方向为x,卫星飞行方向为y,采用四元数来描述影像成像姿态,以四元数微分方程描述姿态变化率,把不同扫描行的瞬时外方位元素描述成以时间为自变量的线性多项式
式中,X(t)为任一时刻t(对应像平面坐标y)的瞬时外方位线元素; X 0为t0时刻(对应像平面坐标y=0)的瞬时外方位线元素;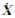 为外方位线元素的一阶变率;
为外方位线元素的一阶变率;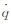 (t)为任一时刻t的瞬时姿态四元数;
(t)为任一时刻t的瞬时姿态四元数;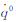 为t0时刻的瞬时姿态四元数;
为t0时刻的瞬时姿态四元数;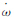 为卫星相对于参考坐标系的旋转角速度所对应的四元数,在卫星扫描的一景影像时间内可视为常数。
为卫星相对于参考坐标系的旋转角速度所对应的四元数,在卫星扫描的一景影像时间内可视为常数。
根据上面的外方位元素表达式,设相机内方位元素(x0,y0)=(0,0),可以建立任意扫描行的瞬时构像方程为
式中,(x,0)为像点坐标;(X,Y,Z)为地面坐标;(XSi,YSi,ZSi)为摄站位置;aji、bji、cji(j=1,2,3)由式(2)确定。上式即为基于四元数微分方程的高分辨率卫星遥感影像成像几何模型。对任意一个控制点,若其对应的像点在影像的第i扫描行,由于其地面坐标(X,Y,Z)已知,有dX=dY=dZ=0。因此,上式的成像几何模型中主要有 X0、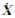 、
、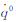 、
、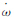 ,共13个未知数,对其线性化可得误差方程式为
,共13个未知数,对其线性化可得误差方程式为
式(7)为利用四元数微分方程求解外方位元素的误差方程。
3.2 独立解算参数的引入四元数在描述影像成像姿态上具有明显的优势,然而在式(7)的误差方程中,四元数的引入使得姿态未知数个数由3个变为4个,而单位四元数的4个分量只有3个独立,因此外方位元素呈现出明显相关,法方程病态。虽然单位四元数的4个分量之间存在一个约束条件,法方程可以通过增加地面控制点数目或带约束条件的参数平差进行求解,但通过未知数之间的约束条件很难从根本上克服其相关性,且不稳定。因此,本文引入3个独立的解算参数,求解过程中不直接求解四元数,而是求解3个解算参数。
解算参数的引入主要是基于四元数的参数替代思想,其基本原理为:四元数构成的矩阵R为正交矩阵,根据RRT=E ,求微分可得dRRT为一反对称矩阵,该反对称矩阵可由3个独立参数(w1,w2,w3)构成,并令dRRT= Sw,于是dR=SwRT,对式(2)的四元数旋转矩阵表达式求微分,可得微分表达式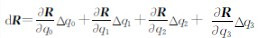 ,进而可以得到
,进而可以得到
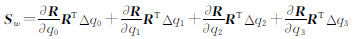
将Sw的表达式展开,通过四元数运算,可以得到3个独立的解算参数(w1,w2,w3)与单位四元数改正数Δq之间的关系为
可以看出,上述关系式与四元数微分方程具有相同的形式。将上面的表达式代入误差方程式(7),可得新的误差方程式为
式中,k′1i、k′2i(i=1,2,…,9)为新的误差方程系数,可由式(7)、式(9)很容易求得,该表达式中同样也完全没有三角函数运算,lx、ly与式(7)相同。误差方程式(10)写成矩阵形式为
式中,V =[vx vy]T; L =[lx ly]T;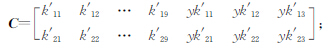

式(11)即为本文求解外方位元素的误差方程,可以看出其形式与摄影测量中常规的误差方程一致,解算参数的引入使得本文方法的未知数个数与常规方法的相同,能有效避免四元数的引入造成的参数相关,并且所需最少控制点个数与常规方法相同,无须采用文献[10]和[13]中带附加条件的参数平差进行求解,只需采用常规的平差方法即可。由于系数表达式中不含三角函数运算,相对于传统的欧拉角模型,该误差方程可以完全避免三角函数运算,提高计算速度。
3.3 Tikhonov正则化理论的方程求解解算参数的引入,可有效消除应用四元数产生的定向参数相关,为进一步克服外方位元素之间可能存在的相关性,本文还采用Tikhonov正则化理论求解误差方程,以提高解算稳定性。
Tikhonov正则化方法是解决病态问题的基础理论,在测量数据处理中具有广泛的应用[18],其实质是通过对一组方程的可接纳解再施以一个弱平滑度约束,以克服病态性,使解算结果稳定和唯一。对于式(11)的误差方程,按Tikhonov正则化理论,其正则化函数为
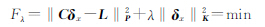
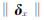 表示δx的范数; K为正则化矩阵,是对称正定阵。对上式进行求解,可得Tikhonov正则化解为
表示δx的范数; K为正则化矩阵,是对称正定阵。对上式进行求解,可得Tikhonov正则化解为
采用Tikhonov正则化方法进行方程求解的关键是确定正则化参数。很多学者对此进行研究,发展了很多算法[18],本文采用广义交叉确认法(generalized cross-validation,GCV)确定正则化参数λ。
3.4 计算过程误差方程式(11)中有12个未知数,因此,至少需要6个控制点才能解算外方位元素,预先给定外方位元素初值,根据Tikhonov正则化理论解算未知数的最或然改正数,再逐步迭代直到改正数小于规定的限差为止。
需要注意的是在平差解算中,直接求解的是解算参数(w1,w2,w3) ,而不是中心扫描行四元数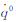 ,预先给定四元数的初值,可计算得到(w1,w2,w3)的值,从而计算得到 Δq ,更新得到新的四元数值,以进行迭代计算。为保证计算过程中四元数始终为单位四元数,即
,预先给定四元数的初值,可计算得到(w1,w2,w3)的值,从而计算得到 Δq ,更新得到新的四元数值,以进行迭代计算。为保证计算过程中四元数始终为单位四元数,即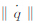 =1,q0采用下式计算得到:
=1,q0采用下式计算得到: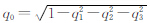 。
。
上述的求解过程可以描述为下面5个步骤:
(1) 读入原始数据,包括内方位元素,像点的观测值及其对应的控制点在地面坐标系中的坐标。
(2) 确定外方位元素的初始值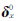 ,通常利用控制点进行仿射变换求得中心扫描行摄站坐标的初值,利用卫星运行的速度计算得到摄站坐标的一阶变率,姿态四元数及其变化率均设为0。
,通常利用控制点进行仿射变换求得中心扫描行摄站坐标的初值,利用卫星运行的速度计算得到摄站坐标的一阶变率,姿态四元数及其变化率均设为0。
(3) 对于每一个控制点,按式(5)确定其外方位元素,并按式(2)计算旋转矩阵。
(4) 利用误差方程式(11)构造设计阵C,常数项L和权阵P ,然后利用式(12)的Tikhonov正则化解求得估值 δx,并通过式(9)求得四元数改正数Δq 。
(5) 更新外方位元素,并判断δ x是否小于限差,若小于限差,则求解过程结束,δ1x为外方位元素的估计值;否则,重复步骤(3)到步骤(4),直至外方位 元素的结果小于限差(一般取限差10-6)为止。
4 试验结果与分析为验证本文基于四元数微分方程的高分辨率卫星遥感影像外方位元素求解算法的有效性和正确性,并与惯用的求解方法(广义岭估计和最小二乘法)及文献[14]中算法进行比较,本文采用SPOT 5影像进行试验计算。
试验数据为中国西部某地区的一景1A级SPOT 5 HRS立体影像,其影像空间分辨率在飞行方向为10 m,在扫描方向为5 m,影像像素大小为12 000×12 000,CCD相机像元大小为6.5 μm× 6.5 μm,前后视相机与铅锤线夹角均为20°。卫星飞行高度约为822 km。在前后视两幅影像上分别量测了27个同名平高地面控制点,均匀分布于整个试验区域,如图 1所示,地面坐标的测量精度为5m,像点坐标在立体环境下人工量测得到。
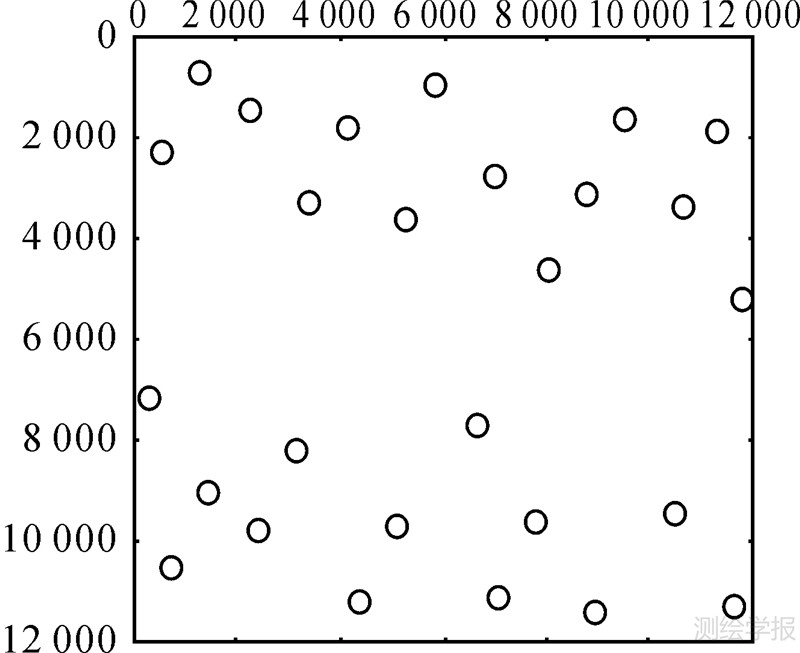
|
| 图 1SPOT 5 HRS立体影像中控制点的分布图(后视影像) Fig. 1 Distributions of ground control points (GCPs) in SPOT 5 HRS stereo images |
本文试验中衡量高分辨率卫星遥感影像外方位元素求解的精度主要采用试验分析法,即对各种方法求解得到的外方位元素值进行如下两类分 析:一是反求像点坐标,计算像点坐标重投影误差的中误差;二是利用空间前方交会求解地面点坐标,计算地面坐标残差的中误差。
试验过程中,为分析不同控制点对外方位元素求解精度的影响,分别采用不同控制点数目进行试验。表 1为根据不同控制点求解得到的外方 位元素值反算像点坐标,计算控制点、检查点的像坐标重投影误差的中误差;表 2为根据不同方案求解的外方位元素值按前方交会计算地面点三维坐标,并计算控制点、检查点的地面坐标残差的中误差。
| 影像 | 点的 类型 | 点数 | x/像素 | y/像素 | ||||||
| LS | GR | YM | QDE | LS | GR | YM | QDE | |||
| 前视 影像 | 控制点 | 6 | 不收敛 | 不收敛 | - | 0.034 | 不收敛 | 不收敛 | - | 0.097 |
| 7 | 不收敛 | 0.306 | 0.261 | 0.081 | 不收敛 | 0.559 | 0.491 | 0.447 | ||
| 13 | 不收敛 | 0.696 | 0.486 | 0.152 | 不收敛 | 0.263 | 0.569 | 0.514 | ||
| 20 | 11.103 | 0.289 | 1.741 | 0.281 | 2.343 | 0.548 | 1.315 | 0.592 | ||
| 27 | 不收敛 | 0.685 | 0.629 | 0.352 | 不收敛 | 0.791 | 0.652 | 0.671 | ||
| 检查点 | 21 | 不收敛 | 不收敛 | - | 0.340 | 不收敛 | 不收敛 | - | 1.203 | |
| 20 | 不收敛 | 0.902 | 0.824 | 0.493 | 不收敛 | 1.119 | 0.982 | 1.002 | ||
| 14 | 不收敛 | 0.659 | 0.843 | 0.253 | 不收敛 | 0.442 | 0.803 | 0.828 | ||
| 7 | 11.788 | 0.291 | 2.051 | 0.295 | 2.365 | 0.696 | 1.407 | 0.731 | ||
| 0 | - | - | - | - | - | - | - | - | ||
| 后视 影像 | 控制点 | 6 | 不收敛 | 不收敛 | - | 0.029 | 不收敛 | 不收敛 | - | 0.074 |
| 7 | 不收敛 | 0.117 | 0.104 | 0.249 | 不收敛 | 0.377 | 0.487 | 0.464 | ||
| 13 | 不收敛 | 0.584 | 0.467 | 0.581 | 不收敛 | 0.431 | 0.464 | 0.457 | ||
| 20 | 1.569 | 0.563 | 0.565 | 0.593 | 1.527 | 0.535 | 0.519 | 0.534 | ||
| 27 | 不收敛 | 0.620 | 2.081 | 0.654 | 不收敛 | 0.555 | 1.434 | 0.572 | ||
| 检查点 | 21 | 不收敛 | 不收敛 | - | 0.903 | 不收敛 | 不收敛 | - | 1.045 | |
| 20 | 不收敛 | 1.171 | 1.412 | 0.904 | 不收敛 | 0.775 | 0.975 | 0.885 | ||
| 14 | 不收敛 | 0.703 | 1.043 | 0.736 | 不收敛 | 0.702 | 0.669 | 0.748 | ||
| 7 | 1.813 | 0.819 | 0.880 | 0.806 | 1.663 | 0.665 | 0.674 | 0.667 | ||
| 0 | - | - | - | - | - | - | - | - | ||
| 注:LS为最小二乘估计,GR为广义岭估计,YM为文献[14]中的算法,QDE为本文的四元数微分方程算法(以下所有图表中均采用此表示);影像像坐标重投影误差的中误差是由利用不同控制点解算的影像外方位元素值反算像坐标,计算其与真值差值的中误差 | ||||||||||
| 点的 类型 | 点数 | x/m | y/m | ||||||
| LS | GR | YM | QDE | LS | GR | YM | QDE | ||
| 控制点 | 6 | 不收敛 | 不收敛 | - | 0.594 | 不收敛 | 不收敛 | - | 1.512 |
| 7 | 不收敛 | 3.685 | 3.127 | 3.857 | 不收敛 | 8.953 | 7.883 | 8.322 | |
| 13 | 不收敛 | 6.231 | 5.264 | 4.827 | 不收敛 | 7.996 | 9.562 | 9.368 | |
| 20 | 45.686 | 5.345 | 10.636 | 5.469 | 27.448 | 10.903 | 14.645 | 11.148 | |
| 27 | 不收敛 | 6.529 | 14.012 | 5.708 | 不收敛 | 14.271 | 23.023 | 12.289 | |
| 检查点 | 21 | 不收敛 | 不收敛 | - | 9.391 | 不收敛 | 不收敛 | - | 19.064 |
| 20 | 不收敛 | 6.609 | 10.628 | 7.793 | 不收敛 | 16.928 | 16.410 | 15.607 | |
| 14 | 不收敛 | 5.210 | 7.651 | 5.219 | 不收敛 | 9.466 | 10.551 | 9.512 | |
| 7 | 25.721 | 3.826 | 8.353 | 4.143 | 13.826 | 6.922 | 8.665 | 7.052 | |
| 0 | - | - | - | - | - | - | - | - | |
| 点的 类型 | 点数 | 平面/m | z/m | ||||||
| LS | GR | YM | QDE | GR | YM | QDE | |||
| 控制点 | 6 | 不收敛 | 不收敛 | - | 1.624 | 不收敛 | 不收敛 | - | 1.241 |
| 7 | 不收敛 | 9.682 | 8.480 | 9.172 | 不收敛 | 7.638 | 6.212 | 5.968 | |
| 13 | 不收敛 | 10.137 | 10.915 | 10.538 | 不收敛 | 7.700 | 7.908 | 7.532 | |
| 20 | 53.297 | 12.143 | 18.101 | 12.417 | 38.385 | 8.308 | 16.724 | 7.787 | |
| 27 | 不收敛 | 15.694 | 26.952 | 13.551 | 不收敛 | 9.918 | 11.161 | 9.507 | |
| 检查点 | 21 | 不收敛 | 不收敛 | - | 21.251 | 不收敛 | 不收敛 | - | 14.249 |
| 20 | 不收敛 | 18.173 | 19.551 | 17.445 | 不收敛 | 14.594 | 12.116 | 11.719 | |
| 14 | 不收敛 | 10.805 | 13.034 | 10.849 | 不收敛 | 8.580 | 8.244 | 8.654 | |
| 7 | 29.201 | 7.909 | 12.036 | 8.179 | 19.873 | 4.966 | 8.850 | 5.159 | |
| 0 | - | - | - | - | - | - | - | - | |
注:n个地面点坐标残差的中误差按下式计算 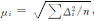 ,Δ为坐标残差,i=X,Y,Z , ,Δ为坐标残差,i=X,Y,Z ,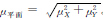 | |||||||||
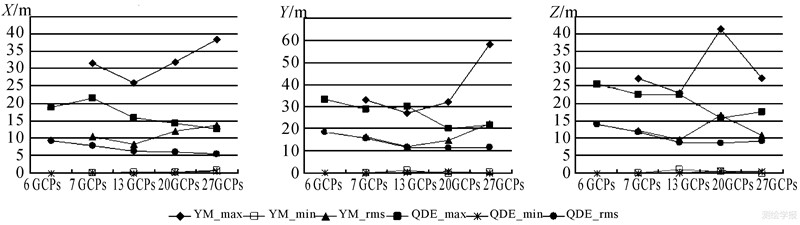
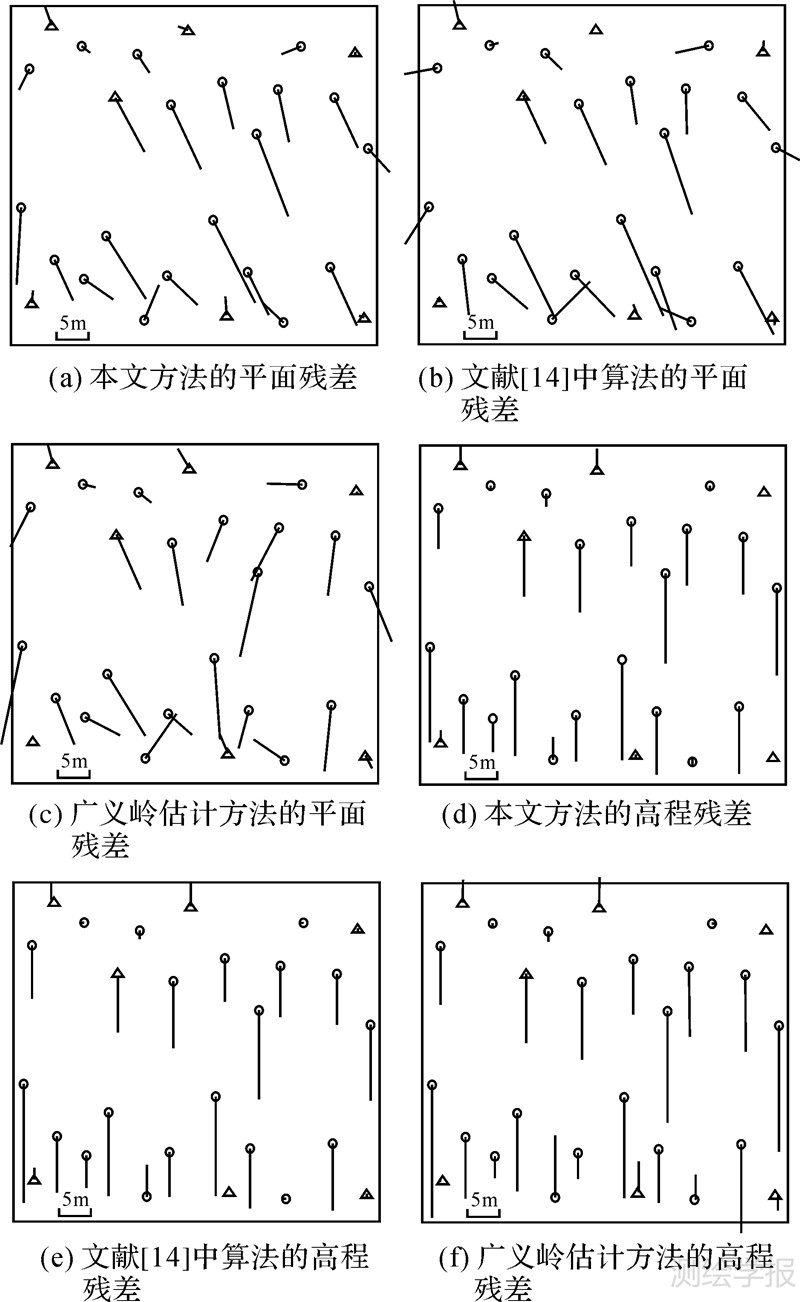
图 2为立体影像中采用不同控制点对文献[14]中算法和本文算法进行定位试验,试验区域中所有地面点定位结果的误差统计图,其中YM_max、YM_min、YM_rms分别为文献[14]中算法的最大残差、 最小残差、中误差,QDE_max、QDE_min 、QDE_rms分别为本文算法的最大残差、最小残差、中误差。图 3为本文方法、文献[14]中算法和广义岭估计3种方法分别利用7个控制点(图中△表示控制点,○表示检查点)参与外方位元素解算,并以此解算结果计算得到所有地面点三维坐标的平面和高程残差分布图。由于篇幅所限,利用其他数目控制点参与解算的结果图不再列出。
|
| 图 2SPOT5 HRS立体像对中不同控制点的定位误差统计图 Fig. 2Orientation error statistical charts of GCPs in SPOT 5 HRS stereo images with different GCPs |
|
| 图 3SPOT5 SPOT5 HRS立体像对中7个控制点时各种方法定位的残差分布图 Fig. 3Coordinate residual charts of GCPs in SPOT 5 HRS stereo images with 7 GCPs |
从上述的解算结果可以看出:
(1) 对于SPOT 5 HRS 立体影像,本文的算法可以求解出其外方位元素,解算精度与广义岭估计相当,和文献[14]中算法相比,更优一些,表明本文中解算参数的引入正确可靠,可有效避免四元数的引入造成的未知数个数增加,对提高精度具有一定作用,同时使得本文方法仅在6 GCPs下也能求解外方位元素;而文献[14]中的算法由于采用四元数增加了未知数个数,必须7 GCPs才能求解;广义岭估计原则上6 GCPs就可求解,但试验中无法求解;最小二乘估计基本都不收敛,仅在20 GCPs时收敛,但解算误差非常大。
(2) 本文方法对控制点数量的需求与广义岭估计、文献[14]中算法基本一致,其求解精度与控制点的数量具有很大关系。当6 GCPs时,本文 方法检查点的平面精度仅为21.251 m,高程精度为14.249 m,精度非常差,随着控制点的增多,精度不断提高,当13 GCPs时,检查点的平面精度达到10.849 m,高程精度为8.654 m,精度得到显著提高。然而控制点继续增加,精度提高也很有限,基本趋于稳定,这一点从图 2也可清楚看出。
(3) 从图 3的7 GCPs参与计算的残差分布图可知,本文方法、广义岭估计和文献[14]中算法定向精度仍带有一定的误差,且具有一定的系统性,这主要是由于控制点和检查点的像坐标在立体环境下人工量测,存在一定的辨认误差和量测误差,同时没有考虑对系统误差进行补偿,若想提高定向精度,需要建立更加严密的成像几何模型,适当考虑系统误差的补偿,进行区域网平差计算,这是进一步需要研究的内容。
5 结束语基于四元数微分方程的外方位元素求解方法的突出特点是计算过程中不直接求解姿态四元数,而是求解独立的解算参数,确保未知数参数个数与现有方法未知数相同,不会增多地面控制点数。利用SPOT5 HRS立体影像的试验结果表明,本文的四元数方法在精度上比文献[14]中算法更优,其原因也正是解算参数的引入从模型上极大地消除了相关性,同时对控制点的要求也和常规方法类似,说明解算参数的引入效果非常显著。此外,从公式中可以看出本文方法完全避免了三角函数运算,相对于现有方法而言,可以有效降低计算复杂度,减少计算时间。随着高分辨率卫星遥感影像的广泛应用,本文方法为其应用提供一种新的技术途径,当然从应用的角度来看,还需要进行更加深入系统的试验,特别是区域网平差试验,这也是本文进一步的研究方向。
| [1] | GONG Jianya. Earth Observation Data Processing and Analysis Research Progress [M]. Wuhan:Wuhan University Press, 2007: 92-97. (龚健雅. 对地观测数据处理与分析研究进展[M]. 武汉:武汉大学出版社, 2007: 92-97.) |
| [2] | KRATKY V. Rigorous Photogrammetric Processing of SPOT Images at CCM Canada [J].ISPRS Journal of Photogrammetry and Remote Senesing, 1989, 44(2):53-71. |
| [3] | WESTIN T. Precision Rectification of SPOT Imagery [J]. Photogrammetric Engineering and Remote Sensing, 1990, 56(2):247-253. |
| [4] | DOWMAN I, MICHALIS P. Generic Rigorous Model for along Track Stereo Satellite Sensors[C] //Proceedings of ISPRS Workshop on High Resolution Mapping from Space.Hanover:[s.n.], 2003. |
| [5] | TOUTIN T. Generation of DSMs from SPOT-5 in-Track HRS and Across-Track HRG Stereo Data Using Spatiotri angulation and Autocalibration[J].ISPRS Journal of Photogrammetry and Remote Senesing, 2006, 60:178-181. |
| [6] | POLI D. Modelling of Spaceborne Linear Array Sensors [D]. Zurich :Swiss Federal Institute of Technology Zurich, 2005. |
| [7] | WESER T, ROTTENSTEINER F, WILLNEFF J, et al. Development and Testing of a Generic Sensor Model for Pushbroom Satellite Imagery[J]. The Photogrammetric Record, 2008, 23(123):255-279. |
| [8] | WILLNEFF J, WESER T, ROTTENSTEINER F, et al. Precise Georeference of Cartosat Imagery via Different Orientation Models[C] //The International Archives of the Photogrammetry, Remote Sensing and Spatial Information Sciences. Beijing:[s.n.],2008:1287-1293. |
| [9] | HISKEN L, MILLER S, TEMPELMANN U, et al. Triangulation of LH Systems ADS40 Imagery Using ORIMA GPS/IMU[C] //ISPRS Commission III Photogrammetric Computer Vision. Graz:[s.n.],2002:1-7. |
| [10] | JIANG Gangwu, JIANG Ting, WANG Yong, et al. Space Resection Independent of Initial Value Based on Unit Quaternions[J]. Acta Geodaetica et Cartographica Sinica, 2007, 36(2):169-175. (江刚武, 姜挺, 王勇,等. 基于单位四元数的无初值依赖空间后方交会[J]. 测绘学报, 2007, 36(2):169-175.) |
| [11] | GUAN Yunlan, CHENG Xiaojun, ZHOU Shijian, et al. A Solution to Space Resection Based on Unit Quaternion[J]. Acta Geodaetica et Cartographica Sinica, 2008, 37(1):30-35. (官云兰, 程效军, 周世健,等. 基于单位四元数的空间后方交会解算[J].测绘学报, 2008, 37(1):30-35.) |
| [12] | LIU Jun, WANG Donghong, ZHANG Yongsheng, et al. Bundle Adjustment of Airborne Three Line Imagery Based on Unit Quaternion [J]. Acta Geodaetica et Cartographica Sinica, 2008, 37(4):451-457. (刘军, 王冬红, 张永生,等. 基于单位四元数的机载三线阵影像光束法平差[J].测绘学报, 2008, 37(4):451-457.) |
| [13] | JIANG Gangwu, JIANG Ting, GONG Hui, et al. Exterior Orientation of Line-Array CCD Images Based on Quaternion Spherical Linear Interpolation [C] //ISPRS TC VII Symposium-100 Years ISPRS. Vienna:[s.n.],2010:74-78. |
| [14] | YAN Li, NIE Qian, ZHAO Zhan. Space Resection of Line Scanner CCD Image Based on the Description of Quaternions[J]. Geomatics and Information Science of Wuhan University, 2010, 35(2):201-204.(闫利, 聂倩, 赵展. 利用四元数描述线阵CCD影像的空间后方交会[J]. 武汉大学学报:信息科学版, 2010, 35(2):201-204.) |
| [15] | ZHOU Jianghua, MIAO Yuhong, LI Hong, et al. Research of Attitude Simulation Using Quaternion [J]. Flight Dynamics, 2000, 12, 18(4):28-32.(周江华, 苗育红, 李宏,等. 四元数在刚体姿态仿真中的应用研究[J]. 飞行力学, 2000, 12, 18(4):28-32.) |
| [16] | ZHAO Yaoxia. Algorithm Study on the Attitude Caught by Inertial Navigation System[J].Mechanical Engineering & Automation, 2006, 3:102-104.(赵耀霞. 惯性导航系统航向姿态计算算法研究[J].机械工程与自动化, 2006, 3:102-104.) |
| [17] | WANG Dechun, CHEN Limin, ZHANG Xiaofan. New Algorithm of Solving Quaternion Diferential Equation [J].Navigation, 2005, 2:96-99.(王德春, 陈利敏, 张孝芳. 解算四元数微分方程的一种新算法[J]. 导航, 2005, 2:96-99.) |
| [18] | WANG Zhenjie. The Regularization Solutions of Ill-Posed Problems in Measurement [M]. Beijing: Science Press, 2006. 66-72. (王振杰. 测量中不适定问题的正则化解法[M]. 北京:科学出版社, 2006: 66-72.) |