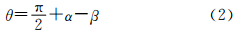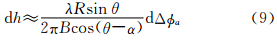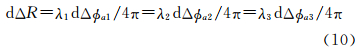2. 中国科学院 电子学研究所 微波成像技术国家级重点实验室，北京 100190
2. National Key Laboratory of Science and Technology on Microwave Imaging，Institute of Electronics, Chinese Academy of Sciences, Beijing 100190,China
1 引 言
合成孔径雷达干涉测量[1, 2, 3](interferometric synthetic aperture radar，InSAR)技术发展迅速，在快速地形测绘和地表形变监测中表现出非凡优势。为了增强对地形陡峭地区的干涉处理能力，提高反演数字高程模型(digital elevation model，DEM)的可靠性和精度，各国研究者已将目光聚焦于多波段、多基线InSAR技术。
在多波段、多基线InSAR处理中，相位解缠仍是一个关键问题。在多波段InSAR相位解缠方面，国内外已有一些研究基础。文献[4] 较早地介绍了利用不同数学方法进行多频(多波段)、多基线InSAR相位解缠的思想；文献[5] 利用两邻近载频扩大相位模糊区间，从而可避免相位模糊，为InSAR处理提供了新思路；文献[6]将最小均方(least mean squares,LMS)用于多波段、多基线InSAR相位解缠；文献[7]将最大似然(maximum likelihood) 方法用于多通道相位解缠。在多波段InSAR获取高精度DEM方面，文献[8, 9, 10, 11, 12, 13, 14]先后进行了研究，通过对多波段干涉数据的组合处理提高高程信息反演精度。
国内机载双天线InSAR系统已成功应用[15]，但尚无专门的多波段InSAR系统，为了促进我国多波段InSAR技术的发展，本文利用由DEM仿真的多波段InSAR干涉图进行了相位解缠研究和试验。依据干涉图零中频矢量滤波能够对密集条纹干涉图进行零中频处理，有效降低干涉条纹频率并得到较好滤波效果的经验[16]，利用较长波长干涉图的解缠结果构建参考干涉图并对较短波长干涉图进行差分处理，降低条纹频率，提高滤波效果，去除相位欠采样，解决频谱混叠，设计了以较长波长干涉图的解缠结果指导较短波长干涉图进行相位解缠的多波段InSAR差分滤波相位解缠方法。通过试验，验证了该方法能把不同波段的干涉数据进行组合处理，可逐步精化解缠结果，从而提高相位解缠的可靠性和精度。
2 多波段InSAR基本原理如图 1所示为InSAR基本几何原理示意图。记主天线相位中心为S1，辅天线相位中心为S2，S1的航高为H，地面点P的高程为h，对应侧视角为θ，S1和S2形成的基线长度为B，基线水平角为α，S1到P的斜距为R，S2到P的斜距为R′，R和R′之间的斜距差为ΔR。
|
| 图 1 InSAR几何示意图 Fig. 1 Sketch map of InSAR geometry |
根据InSAR基本原理可知，P点高程h为
式中
在△S1S2P中，根据余弦定理有
则β为
联立式(1)、(2)和式(4)，可得
对于单发双收式的InSAR系统，ΔR与理论干涉相位Δφa的关系为
此时
对于单发单收式的InSAR系统，ΔR与理论干涉相位Δφa的关系为
由式(7)、(9)可知，波长λ越短，等量的高程变化对应的相位变化越大，干涉相位越容易出现欠采样，相位解缠越难；但是，波长λ越短，所能反演的高程精度越高。
为了分析问题方便，假定所采用的是三波段重复轨道InSAR系统，各波段的系统参数仅波长不同。令波长分别为λ1、λ2和λ3，则有
因此
3 多波段InSAR差分滤波相位解缠方法
各波段干涉图之间的精确匹配是成功进行差分滤波相位解缠的基础。为了确保干涉图的子像元级配准，可将波长最长InSAR主影像作为基准影像，采用强度影像相关系数匹配与最小二乘匹配相结合的策略，对其余各影像进行准配和重采样，再计算以最长波长主影像为基准的各干涉图。
假定各波段波长由长至短依次排列为λ1,λ2,…,λN(N为波段数)，相应的N幅干涉图分别为Inter1,Inter2,…,InterN。根据对InSAR基本原理的分析可知：在相位噪声相当的情况下，由最长波长获取的干涉图Inter1条纹最稀疏，干涉质量最好，相位解缠最容易；由最短波长获取的干涉图InterN条纹最密集，干涉质量最差，相位解缠最困难。
由式(11)可知，干涉图Interi(i=1,2,…,N)和Interj(j=1,2,…,N;j>i)对应像元处的真实干涉相位微分存在如下关系
式(12)表明任意两波段干涉图中对应的真实干涉相位微分与波长成反比。实际情况下，由于噪声因素的影响，解缠后的干涉相位微分不能严格满足此式。
在最长波长干涉图已正确解缠的基础上，为了提高对较短波长、较高频率干涉图的解缠效果，可根据式(12)，逐点计算其解缠后的干涉相位微分参考值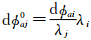
，再将较短波长的干涉图与该参考值进行差分处理，从而降低干涉条纹频率，提高干涉图滤波效果和干涉质量，减少干涉相位欠采样，解决频谱混叠，提高相位解缠质量。
在进行差分处理时，需要利用较长波长干涉图Interi的解缠干涉相位φi来构造较短波长干涉图Interj的基准干涉图Interj0，相应像元的相位值φj0为
再将干涉图Interj与基准干涉图Interj0作差分，得到差分干涉图DInterj
通过差分处理，可以降低较短波长干涉图的干涉条纹频率，减少相位欠采样，解决频谱混叠问题。干涉图Interj中包含高精度高程信息的高频部分被有效地降低到低频，既有利于滤波处理又有利于相位解缠。
对差分干涉图DInterj进行滤波后，可进行高质量的相位解缠，再结合基准干涉图Interj0，得到干涉图Interj的解缠结果。
按照上述思想，本文设计的多波段InSAR差分滤波相位解缠流程如图 2所示。从最长波长干涉图Inter1的滤波和相位解缠出发，依次进行差分滤波和相位解缠，直至最短波长干涉图InterN解缠完毕。
|
| 图 2 多波段InSAR差分滤波相位解缠流程 Fig. 2 Flowchart of phase unwrapping with difference filter for multi-band InSAR |
多波段InSAR差分滤波相位解缠主要包括以下关键步骤：
(1) 利用频率域低通滤波或者空间域(零中频)矢量滤波等方法对最长波长、最低频率的干涉图Inter1进行滤波处理。
(2) 计算相干图、伪相干图或残差点图等干涉质量图。
(3) 采用质量图区域生长、直接相位积分和移动曲面相位拟合相结合的自适应相位解缠方法对滤波后的干涉图Inter1进行相位解缠。
(4) 利用干涉图Inter1的解缠结果，根据波长λ2与波长λ1之间的比例关系，构建基准干涉图Inter20。若以φ(mod2π)表示按2π对φ求模，则基准干涉图中各像素的相位值φ20与干涉图Inter1解缠结果中各像素相位值φ1之间的关系为
(5)将干涉图Inter2与基准干涉图Inter20中相应像素处的相位值作差分，得到差分干涉图DInter2
(6) 采用频率域低通滤波或空间域矢量滤波等方法对差分干涉图 2进行滤波处理；
(7) 采用质量图区域生长、直接相位积分和移动曲面相位拟合相结合的自适应相位解缠方法对滤波后的差分干涉图 2进行相位解缠；
(8) 由差分干涉图解缠结果和基准干涉图得到干涉图 2的解缠结果；
(9) 参照步骤(4)-(8)，依次由较长波长干涉图的解缠结果指导较短波长干涉图的相位解缠，直至最短波长干涉图解缠完毕。
4 试 验为了验证所设计的多波段InSAR差分滤波相位解缠方法的有效性，采用由不同地区DEM仿真的多波段干涉图进行了相位解缠试验。仿真多波段InSAR干涉图所用的DEM之一为由网上免费下载的海南某地区SRTM 90 m格网间距的DEM，其灰度图如图 3所示，相关仿真参数如表 1所示。在进行多波段干涉图仿真时，加入了均值为0，方差为0.039 5 rad2的相位噪声。
|
| 图 3 SRTM 90 m间距的DEM Fig. 3 SRTM DEM spacing 90 meters |
| 参数类型 | 参数值 |
| DEM格网间距/m | 90 |
| 宽/point | 1024 |
| 高/point | 1024 |
| 基线长度/m | 20 |
| 基线水平角/(°) | 0 |
| 波长1/m | 0.18 |
| 波长2/m | 0.09 |
| 波长3/m | 0.06 |
| 航高/m | 233 000.0 |
| 多普勒中心频率/Hz | 0 |
| 干涉图方位向尺寸/m | 90 |
| 干涉图距离向尺寸/m | 90 |
| 中心侧视角/(°) | 23 |
| 相位噪声均值/rad | 0 |
| 相位噪声方差/rad2 | 0.039 5 |
图 4(a)至图(c)为仿真的多波段干涉图，干涉图大小如表 2所示。图 4(d)为干涉图 1的矢量滤波结果，图 4(e)为干涉图 1的解缠结果，图 4(f)为根据波长比例关系由干涉图 1的解缠结果构建的基准(模糊)干涉图 2，图 4(g)为干涉图 2与基准干涉图 2作差分得到的差分干涉图 2，图 4(h)为差分干涉图 2的矢量滤波结果，图 4(i)为由差分干涉图 2解缠结果和基准干涉图得到的干涉图 2的解缠结果，图 4(j)为由干涉图 2的解缠结果构建的基准(模糊)干涉图 3，图 4(k)为干涉图 3与基准干涉图 3作差分得到的差分干涉图 3，图 4(l)为差分干涉图 3的矢量滤波结果，图 4(m)为由差分干涉图 3解缠结果和基准干涉图得到的干涉图 3的解缠结果。
|
| 图 4 相位解缠各步骤成果图 Fig. 4 Results in each step of phase unwrapping |
为了充分说明基于差分滤波的多波段InSAR相位解缠方法在解决干涉相位欠采样处的解缠能力和对噪声的稳健性，分别对上述试验结果按较大比例进行了显示，结果如图 5所示。从放大的试验结果可以清楚地看到，由最短波长干涉图获取的解缠结果细节最丰富，这也表明由最短波长获取的干涉图进行高程信息反演时精度最高。
|
| 图 5 局部放大成果图 Fig. 5 Local results zoomed in |
由于对最短波长的干涉图进行相位解缠最难，因此从最短波长干涉图的解缠效果即可说明整体解缠效果。为了验证本文方法有效，根据DEM计算了不含噪声的最短波长干涉图的理论解缠结果，如图 6所示，对应的局部放大结果如图 7所示。对比图 4(m)与图 6，图 5(f)与图 7，可以发现，本文的解缠结果与理论解缠结果一致，充分验证了本文方法的有效性。
|
| 图 6 理论解缠结果 Fig. 6 Theoretical phase unwrapping result |
|
| 图 7 局部放大的理论解缠结果 Fig. 7 Theoretical phase unwrapping result zoomed in |
为了验证本文多波段相位解缠方法相比于传统单波段相位解缠方法的优势，对图 4(c)中的干涉图进行滤波之后，分别采用质量图区域生长方法和直接相位积分方法进行了相位解缠。通过试验，对于该干涉图，当相干性阈值取0.93时，由给定的高相干点进行区域生长没有解缠错误的点和误差传递，此时的解缠结果如图 8所示，相应的局部放大结果如图 10所示。采用直接相位积分方法的解缠结果如图 9所示，相应的局部放大结果如图 11所示。对比图 5(f)、图 10、图 11可以发现，采用多波段差分滤波相位解缠方法可以对欠采样区域进行有效解缠，而采用传统单波段解缠方法会无法解缠或者出现解缠错误和误差传递，从而验证了多波段InSAR差分滤波相位解缠方法能够依据差分滤波策略，有效降低较短波长干涉条纹频率，减少相位欠采样，解决干涉图频谱混叠问题，从而解决短波长干涉图欠采样区域相位解缠难题。
|
| 图 8 区域生长单波段解缠结果 Fig. 8 Phase unwrapping result of single band with region growing |
|
| 图 9 直接相位积分单波段解缠结果 Fig. 9 Phase unwrapping result of single band with direct integral |
|
| 图 10 局部放大的区域生长解缠结果 Fig. 10 Phase unwrapping result zoomed in with region growing |
|
| 图 11 局部放大的直接积分解缠结果 Fig. 11 Phase unwrapping result zoomed in with direct integral |
为了定量说明差分滤波相位解缠方法在解决欠采样问题方面的优势，分别统计了原始干涉图、滤波后干涉图和差分滤波后干涉图的残差点数目。各干涉图的残差点数目如表 3所示。由表 3的统计结果可以看出：相对于传统单波段干涉图滤波方法，采用多波段干涉图差分滤波方法能更加有效地降低残差点数目，从而为可靠的相位解缠奠定了基础。
| 干涉图类型 | 正残差点数 | 负残差点数 | |
| 滤波前 | 492 | 496 | |
| 干涉图1 | 直接滤波后 | 9 | 9 |
| - | - | - | |
| 滤波前 | 581 | 584 | |
| 干涉图2 | 直接滤波后 | 18 | 18 |
| 差分滤波后 | 5 | 2 | |
| 滤波前 | 1 010 | 1 008 | |
| 干涉图3 | 直接滤波后 | 103 | 105 |
| 差分滤波后 | 4 | 4 | |
本文中，在采用差分滤波方法进行多波段InSAR相位解缠时，对于每幅差分滤波后的干涉图均采用直接相位积分方法进行相位的积分和解缠处理，为了客观、定量地比较该方法相对于传统单波段相位解缠方法的优势，在对每幅干涉图进行单波段相位解缠时也采用了直接相位积分解缠方法。由于干涉图 3的结果更能说明两种方法的差异，在表 4中给出了两种方法的解缠结果与理论结果之差的方差。从表 4中可以明显看出，在噪声水平相同的情况下，多波段InSAR差分滤波相位解缠方法明显优于单波段相位解缠方法。
| 干涉图名 | 解缠方法 | 差的方差/rad2 |
| 干涉图3 | 直接积分解缠 | 6.863 684 |
| 差分滤波解缠 | 0.186 814 |
通过对仿真的多波段InSAR干涉图进行相位解缠试验，可以发现，在噪声水平相同的情况下，采用新提出的差分滤波相位解缠方法，可以由较长波长干涉图的解缠结果指导较短波长干涉图的相位解缠，从而解决干涉相位欠采样区域的相位解缠难题，并且该方法对相位噪声具有一定的稳健性。
但是，在应用该解缠方案时，要求最长波长干涉图中不存在干涉相位欠采样，以保证其可解缠性，并且在相位解缠过程中，较低频干涉图的解缠结果会影响较高频干涉图的相位解缠质量。
5 总 结本文设计了多波段InSAR差分滤波相位解缠方法，采用由SRTM DEM仿真的多波段干涉图进行了相位解缠试验，得到了满意的相位解缠结果，验证了其有效性。
在后续研究中，将进一步研究地形起伏状况对波长组合要求和相位解缠的影响，研究最佳波长组合，为多波段InSAR系统设计提供辅助决策信息。
| [1] | GRAHAM L C. Synthetic Interferometer Radar for Topographic Mapping[J]. Proceedings of the IEEE, 1974, 62(6):763-768. |
| [2] | WANG Chao, ZHANG Hong, LIU Zhi. Spaceborne Synthetic Aperture Radar Intreferometry[M]. Beijing: Science Press,2002. (王超,张红,刘智. 星载合成孔径雷达干涉测量[M]. 北京:科学出版社, 2002.) |
| [3] | JIN Guowang. Research on Key Processing Techniques for Accurate DEM Deriving from InSAR [D]. Zhengzhou: Institute of Surveying and Mapping, Information Engineering University, 2007. (靳国旺. InSAR获取高精度DEM关键处理技术研究[D]. 郑州: 信息工程大学测绘学院, 2007.) |
| [4] | XU W, CHANG C, KWOH L K, et al.Phase Unwrapping of SAR Interferogram with Multi-frequency or Multi-baseline[C]//Proceedings of IEEE International Geoscience and Remote Sensing Symposium, IGARSS’ 94. Pasadena: IEEE Computer Society, 1994:730-732. |
| [5] | SCHMITT K, WIESBECK W.An Interferometric SAR Processor Avoiding Phase Ambiguities[C]//Proceedings of IEEE International Geoscience and Remote Sensing Symposium, IGARSS’ 97.Florence: IEEE Computer Society, 1997: 1713-1715. |
| [6] | VINOGRADOV M V, ELIZAVETIN I V. Phase Unwrapping Method for the Multifrequency and Multibaseline Interferometry[C]//Proceedings of IEEE International Geoscience and Remote Sensing Symposium, IGARSS’ 98. Seattle: IEEE Computer Society,1998:1103-1105. |
| [7] | FORNARO G, PAUCIULLO A. Phase Difference-based Multichannel Phase Unwrapping[J]. IEEE Transactions on Image Processing, 2005,14(7):960-972. |
| [8] | LANARI R, FORNARO G. Generation of Digital Elevation Models by Using SIR-C/X-SAR Multifrequency Two-pass Interferometry:the Etna Case Study[J]. IEEE Transactions on Geoscience and Remote Sensing, 1996, 34(5):1097-1114. |
| [9] | EINEDER M, ADAM N. Avoiding Phase Unwrapping in DEM Generation by Fusing Multi-frequency Ascending and Descending Interferograms[C]//Proceedings of IEEE International Geoscience and Remote Sensing Symposium, IGARSS’ 04. Anchorage: IEEE Computer Society, 2004:477-480. |
| [10] | EINEDER M, KRIEGER G. Interferometric Digital Elevation Model Reconstruction:Experiences from SRTM and Multi-channel Approaches for Future Missions[C]//Proceedings of IEEE International Geoscience and Remote Sensing Symposium, IGARSS’ 05.Seoul: IEEE Computer Society, 2005:2264-2267. |
| [11] | PASCAZIO V, SCHIRINZI G. Estimation of Terrain Elevation by Multifrequency Interferometric Wide Band SAR Data[J].IEEE Signal Processing Letters, 2001,8(1):7-9. |
| [12] | De ZAN F, FORNARO G, GUARNIERI A M, et al. Coherent Techniques for Multi Channel SAR Interferometry//Proceedings of IEEE International Geoscience and Remote Sensing Symposium, IGARSS’ 05.Seoul: IEEE Computer Society, 2005:1191-1194. |
| [13] | WANG Wei. Height Reconstruction Using Multifrequency InSAR Data[D]. Harbin: Harbin Institute of Technology,2006. (王伟.多频率InSAR高程信息重建算法研究[D]. 哈尔滨:哈尔滨工业大学,2006.) |
| [14] | LIU Nan, ZHANG Linrang, ZHANG Juan, et al. Multifrequency-multibaseline MIMO InSAR and Its Performance Analysis[J]. Systems Engineering and Electronics, 2009,31(9): 2090-2095. (刘楠, 张林让, 张娟,等.多频-多基线MIMO InSAR及其性能分析[J].系统工程与电子技术,2009,31(9):2090-2095.) |
| [15] | JIN Guowang, ZHANG Wei, XIANG Maosheng, et al. A New Calibration Algorithm of Interferometric Parameters for Dual-antenna Airborne InSAR [J]. Acta Geodaetica et Cartographica Sinica, 2010,39(1):76-81.(靳国旺,张薇,向茂生,等. 一种机载双天线InSAR干涉参数定标新方法[J]. 测绘学报,2010,39(1):76-81.) |
| [16] | JIN Guowang, XU Qing, ZHANG Yan, et al. The Zero Intermediate Frequency Vector Filtering for Interferograms[J]. Acta Geodaetica et Cartographica Sinica, 2006,35(1):24-29.(靳国旺,徐青,张燕,等. InSAR干涉图的零中频矢量滤波方法[J].测绘学报, 2006,35(1):24-29.) |