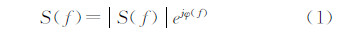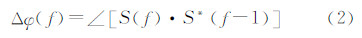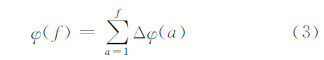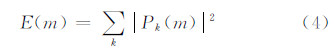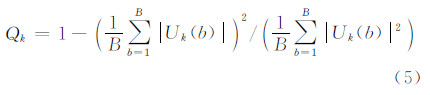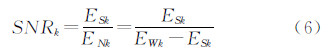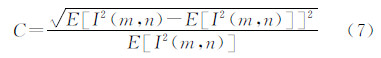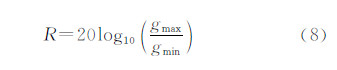2. 中国科学院 电子学研究所, 北京100190
2. Institute of Electronics, Chinese Academy of Sciences, Beijing 100190, China
1 引 言
在合成孔径雷达(synthetic aperture radar,SAR)成像过程中,载机的运动误差会使回波多普勒信号产生相位误差,造成图像散焦,最终影响图像质量[1]。全球定位系统(global positioning system,GPS)和惯导系统(inertial navigation system,INS)可以测得载机的运动误差,但当图像分辨率变高时,GPS和INS的测量精度已不能满足成像的要求。通常先用GPS和INS的测量数据进行粗补偿,然后再利用基于回波数据的自聚焦算法进行精补偿。常用的自聚焦算法有子孔径算法[2]、对比度最优法[3]、秩-相位误差法[4]和相位梯度自聚焦(phase gradient autofocus,PGA)算法[5]等。子孔径算法和对比度最优法对二次相位误差的估计效果好,且运算量小,缺点是随着相位误差阶数增大而逐渐失效。秩-相位误差法能够估计任意阶的相位误差,但是其信号模型基于这样一个假设:一个距离单元只有一个强散射点,而实际中的场景很难符合这一模型。PGA算法基于图像中的特显点来提取相位误差,补偿整幅图像,它对任意阶误差都有效,且对随机误差也能进行较好的补偿。所以,PGA算法已经在实际应用中取得了良好的效果。
原始的PGA算法[5]提出了两种加窗的方法,一种方法是首先计算方位向的能量分布,然后把该能量分布下降到-10dB处的长度扩展50%作为窗宽;另一种方法是首先取一个较大的窗宽,然后每次迭代时将窗宽按一定比例递减。但这两种方法都不是根据实际支撑域来选取窗宽,窗宽选取不当会造成误差估计不准,最终导致图像聚焦性能降低。本文提出的方法,先计算方位向的平均能量分布,然后把该能量分布下降到平均能量处的长度作为窗宽。这种选取窗宽的方法可以根据图像的特征自适应地调整窗宽,提高图像聚焦性能。原始的PGA算法挑选的特显点是能量较高的距离单元中的强散射点,但这种方法挑选的散射点可能由于周围有较强的杂波干扰而不是孤立的,而用这种质量较差的散射点估计相位误差也会影响图像的聚焦效果。文献[6]对原始的PGA算法的特显点选取方法进行了一些改进,提出了QPGA算法,这种方法能够更大概率地选出孤立特显点。本文在QPGA算法的基础上,首先判断每个特显点的信杂比,然后选出信杂比大的特显点,从而提高相位误差估计精度,最终提高图像的聚焦质量。
2 PGA算法原理PGA算法的基本原理[7]是,从SAR复图像中找到一些孤立的强散射点,对每个强散射点进行加窗,并估计它的相位误差,然后对这些估计结果取平均。同样的操作进行若干次迭代,便可得到方位向的相位误差曲线[8]。经典PGA算法的步骤如下所示:
(1) 特显点的选择。因为只有孤立的强散射点才能保证高信杂比,所以首先从每个距离单元里各选出一个孤立的强散射点。因为能量大的特显点通常具有高信杂比,所以原始的PGA算法是选择众多距离单元里能量比较高的散射点作为特显点。但如果场景中有大片能量很强的面目标时,用这种方法挑选出来的散射点不是孤立的,其周围会存在很强的杂波干扰,这样会影响所估计相位误差的准确性,最终影响到相位误差的校正和图像的聚焦效果。鉴于此,QPGA算法阐述了一种基于对比度测量的选取特显点的方法,它选取对比度最大的强散射点作为特显点,这样可以把具有强杂波干扰的点给剔除掉,有效地避免原始PGA算法特显点选取方法的短处。
(2) 圆移操作。为了去掉各个特显点所对应的线性调频信号相位中的线性项,通过圆移操作使各个特显点的峰值位于方位向左端点的位置。
(3) 加窗操作。为了提高每个特显点的信杂比,对经过圆移操作的所有距离单元的特显点统一加窗。原始的PGA算法有两种常见的加窗方法。一种方法是首先计算方位向的能量分布,然后计算能量从最大值下降到-10dB时的长度,再把此长度扩张50%作为最终的窗长;另一种方法是首先选取一个足够大的窗长,然后将此窗长在后续的迭代中逐次递减20%,直至图像聚焦或窗长减小到一定阈值以下。加窗操作对于提高PGA算法的鲁棒性起到了重要的作用,不正确的窗长度往往会造成相位误差的估计产生偏差。如果窗长度选择过大,那么处理区域内的信杂比便会降低,不仅造成迭代次数增加,而且影响相位误差估计的准确性。如果窗长度选择过小,即截取到不完整的散焦区域,将导致所估计相位误差失真,严重时甚至会造成估计的发散。此外,PGA算法的良好聚焦性能是建立在合适的统计模型和高信杂比的基础上的。当在目标点附近存在着其他强散射点时,即使窗长度选得很小,窗内的信杂比仍然会较低,这会引起所估计相位不准确,甚至导致迭代结果不收敛。这跟特选点的选取有关。
(4) 计算相位误差。记加窗操作后的点目标[8]为s(n),对s(n)作傅里叶变换,得到式(1)
式中,n是时域的方位向坐标;f是频域的方位向坐标;φ(f)为频域的方位向相位误差,计算它的相位梯度,如式(2)所示[9] 式中,∠代表取角操作;*代表取共轭。因为这些距离单元里的φ(f)可以认为是相同的[10],所以对每个距离单元所估计出的相位误差梯度Δφ(f)作取平均操作[11],作为该次相位误差梯度的估计结果,取平均后的相位误差梯度仍然记作Δφ(f)。
对相位误差梯度Δφ(f)求和,便可得到相位误差φ(f)
(5) 对相位误差进行校正。用上面估计的相位误差φ(f)来补偿S(f),并进行逆傅里叶变换,便可得到相位误差校正后的复图像。
(6) 迭代。对以上5个步骤进行迭代,直至完成相位误差的估计和校正。
3 改进的PGA算法 3.1 加窗方法的改进根据上节的分析,窗宽的选取对于算法收敛速度和所能达到的精度都有一定影响。本文列举几种常见的加窗方法,对它们的性能进行相应的分析,并提出一种新的加窗方法。如式(4)所示,在对复图像进行中心移位之后,把各距离行上的能量累加,便可获得方位向的能量分布[12]。
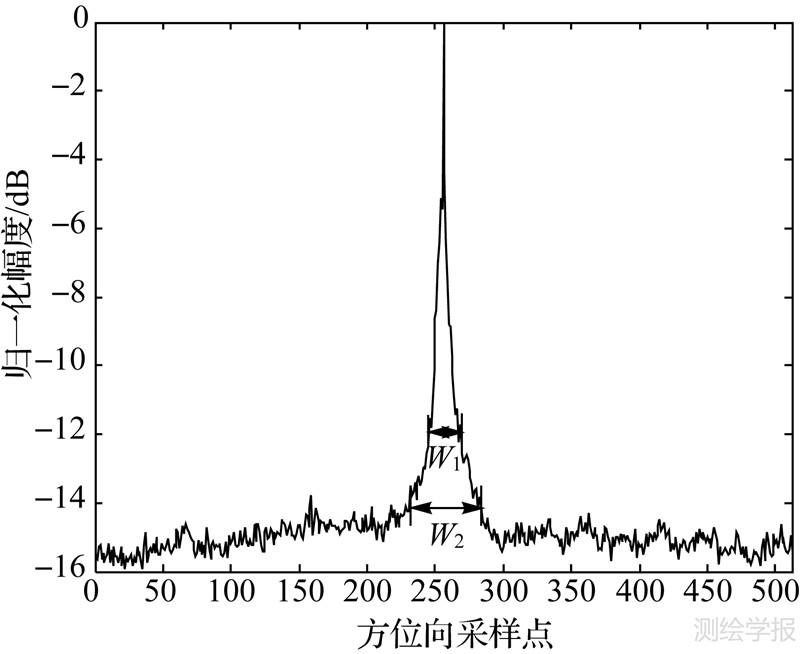
式中,Pk(m)是经过中心移位的第k行数据,所得到的方位向能量分布E(m)形状如图 1 所示,可以看到E(m)在中间的幅度最大,在其两侧的幅度则迅速下降,直到趋于平稳。
|
| 图 1 本文方法的方位向能量分布 Fig. 1 Azimuth energy distribution of the modified method |
根据方位向的能量分布图,可以判断出相位误差点扩展函数的支撑域。从上节的分析可知,为了提高算法的收敛速度和所能达到的估计精度,所加的窗宽应该尽量接近支撑域的大小。原始的PGA算法提出了两种常用的加窗方法,下面分析这两种方法的性能。
第1种加窗方法假设支撑域外的平均能量Ea为-10dB,而实际上不同图像一般具有不同的Ea值,并且随着迭代次数增加,Ea的值也会发生改变。例如在图 1中,Ea大约在-14dB左右,这时如果选择Ea为-10 dB加窗,则相位误差的点扩展函数的一部分由于处在窗外而被舍去,造成相位误差的估计不准确。
第2种加窗方法不是根据实际支撑域来选取窗宽,这样的操作虽然简单,但是缺乏针对性,因此也可能造成聚焦性能下降。
本文提出一种新的窗宽选取方法。首先,计算方位向的平均能量ΣE(m)/N(其中,N表示E(m)的长度),把它作为支撑域外的平均能量Ea。然后,选取E(m)下降到Ea处的窗宽W作为所加窗宽。和上面两种加窗方法相比,它能够更准确地估计相位误差点扩展函数的支撑域。每次迭代时都用此方法来估计窗宽,若本次迭代计算的窗宽不小于前次迭代的窗宽,则把前次迭代窗宽的80%作为本次迭代的窗宽,以此来保证迭代的收敛性。如图 1所示,W1是取Ea为-10 dB所估计的窗宽,窗宽过小,使得相位误差点扩展函数的一部分处于窗外而被舍去,造成相位误差估计有误。W2是用本文方法所估计的窗宽,窗宽适中,这有助于提高算法的收敛速度和估计精度。
3.2 距离门选取方法的改进当目标点附近存在其他强点时,即使窗宽选得很小,信杂比依然会很低,这将引起所估相位误差不准,甚至导致迭代不收敛。舍弃信杂比小的距离门可以提高算法的精度。此处的信杂比是指所加窗口内的信杂比。原始PGA算法选取距离单元里能量较大的散射点作为特显点,QPGA算法在距离压缩相位历史域计算对比度[13],如式(5)所示,选择Qk较小的距离行作为估计相位误差所用的距离行
式中,B是信号的长度;Uk(b)是第b个距离门的距离压缩相位历史域响应。本文在QPGA算法的基础上,首先判断每个特显点的信杂比,然后选出信杂比大的特显点,进而提高聚焦质量。记所选取的距离行总数为K,对于某个距离行k,由上步得到了窗宽W,记窗宽W内的能量为EWk,取宽度为0.6W的窗口内的能量为信号能量,记作ESk,将EWk和ESk的差值作为噪声的能量ENk = EWk - ESk。这样,每个距离行的信杂比可以写成
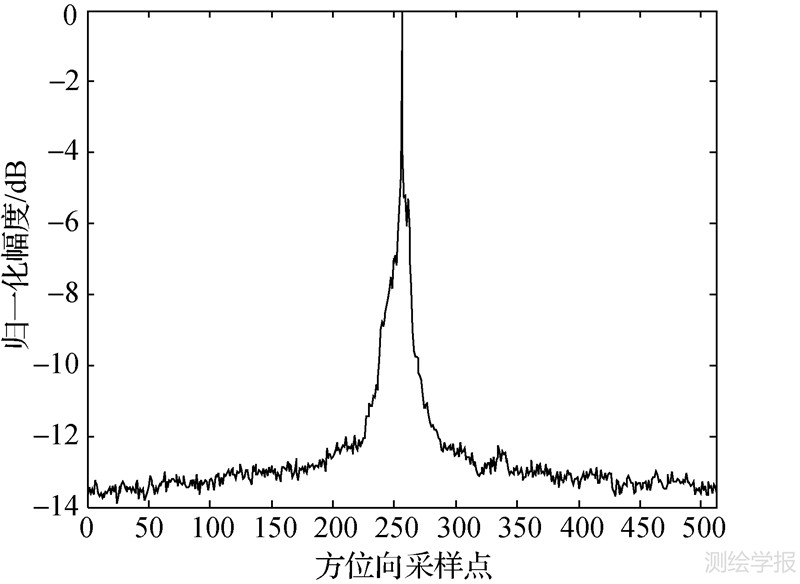
对每一个距离门,分别依此方法计算信杂比。把各个距离门的信杂比排序,舍掉信杂比较小的距离门。对于信杂比大的距离门,用式(4)重新计算E(m),可以看出,新的E(m)(如图 1所示)明显比原来的E(m) (如图 2所示)的信杂比要大。然后用上面的改进方法计算窗宽,用信杂比大的距离门来估计相位误差。通过选取合适的距离门进行相位误差估计,使算法在低信杂比的条件下也能取得较好的聚焦性能。
|
| 图 2 传统方法的方位向能量分布 Fig. 2 Azimuth energy distribution of the traditional method |
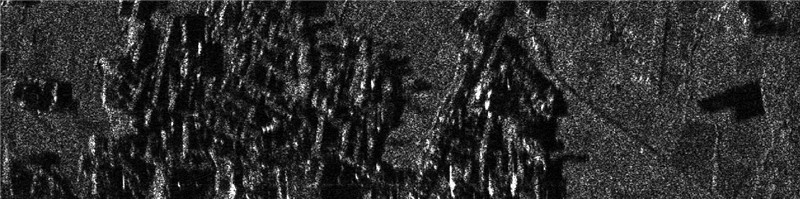
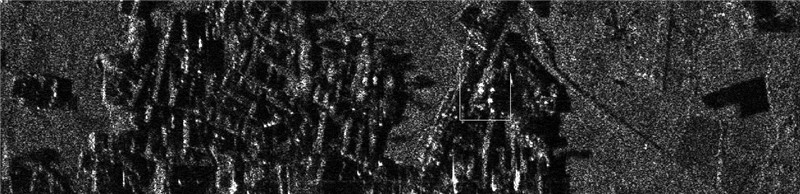
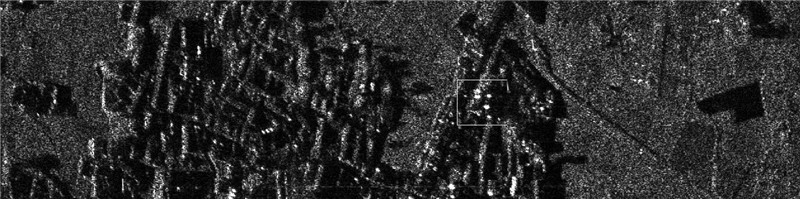
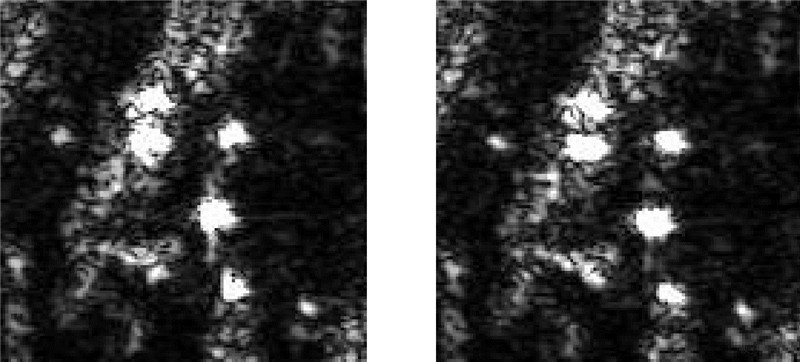
这里采用实际的SAR图像来验证本文方法的性能。图 4是没有用自聚焦方法的散焦图像;图 5是用原始的PGA算法聚焦后的图像,计算E(m)降至-10 dB的长度L,然后将L增加50%作为窗长,距离行的选择采用能量最大准则;图 6是用第2种加窗方法的原始PGA算法聚焦后的图像,取一个较大的窗长,然后将窗长以一定比例递减,距离行的选择采用能量最大准则,这种情况简记为“原始PGA2”;图 7是用QPGA算法聚焦后的图像,取一个较大的窗长,然后将窗长以一定比例递减,距离行的选择采用对比度准则;图 8是用本文方法聚焦以后的结果,窗宽的选择采用本文的改进方法,距离行的选择也采用本文的改进方法,留下信杂比大的特显点,舍弃信杂比小的信杂点。图 9~13分别是图 4~8白框内的细节部分。在各图像中,横向是距离向,纵向是方位向。可以看出,本文方法比原始的PGA和QPGA的聚焦效果都要好,表 1列出了几种方法所得到图像的对比度和动态范围。本文方法得到的图像对比度和动态范围都是最大的,这与图像的视觉效果也是一致的。表 2是几种算法的比较说明。

|
| 图 3 散焦图像 Fig. 3 Defocus image |
|
| 图 4 原始PGA聚焦后的图像 Fig. 4 Image processed by the original PGA |

|
| 图 5 原始PGA2聚焦后的图像 Fig. 5 Image processed by the original PGA2 |
|
| 图 6 QPGA聚焦后的图像 Fig. 6 Image processed by the QPGA |
|
| 图 7 本文方法聚焦后的图像 Fig. 7 Image processed by the modified algorithm |

|
| 图 8 散焦图像 图9 原始PGA 图10 原始PGA2 Fig. 8 Defocus Fig.9 Original PGA Fig.10 Original PGA2 |
|
| 图 11 QPGA 图12 本文方法 Fig. 11 QPGA Fig.12 Modified algorithm |
| 原始 图像 | 原始 PGA | 原始 PGA2 | QPGA | 本文 方法 | |
| 图像对比度 | 24.94 | 37.62 | 39.67 | 45.91 | 48.89 |
| 图像动态 范围/dB | 77.42 | 80.46 | 83.14 | 85.54 | 89.50 |
| 原始PGA | 原始PGA2 | QPGA | 本文方法 | |
| 加窗 | 计算E(m)降 至-10 dB的长 度L,然后将L 增加50%作 为窗长 | 取一个较大的 窗长,然后将 窗长以一定比 例递减 | 取一个较大的 窗长,然后将 窗长以一定比 例递减 | 本文的 改进方法 |
| 特显点 选择 | 能量最大准则 | 能量最大准则 | 对比度准则 | 本文的 改进方法 |
图像对比度的定义[14]如式(7)所示
式中,C、I2(m,n)、E[·]分别表示图像的对比度、第(m,n)个像素的强度以及图像强度的均值。图像动态范围R定义[15]为图像最大可检测的灰度值gmax与最小可检测的灰度值gmin(非零值)之比。如果图像数据是幅度数据,则可表示为
5 结 论原始PGA算法的加窗方式有一定局限性,本文提出的方法,首先计算方位向的平均能量,然后计算方位向的能量分布下降到平均能量处的长度,并以此长度作为所加窗宽。这种窗宽选择方法能够根据不同图像的特征自适应地选取窗宽,提高聚焦效果。原始PGA挑选的特显点是能量较高的距离单元中的强点,但这样挑选的散射点周围可能会有较强的杂波干扰,所以不是孤立的,而用这种质量较差的散射点估计相位误差会降低散焦性能。QPGA算法对原始PGA算法的特显点选取方法进行了改进,保证了孤立特显点存在的可能性比较大。本文在QPGA算法的基础上,判断每个特显点的信杂比,选出信杂比大的特显点,来提高聚焦质量。试验结果表明,该方法能在一定程度上改善PGA 算法的收敛速度和聚焦效果。
| [1] | YANG Yonghong, PI Yiming. Motion Error of Spaceborne-airborne Hybrid Bistatic SAR[J]. Acta Geodaetiea et Cartographica Sinica, 2008, 37(2): 163-167. (杨永红, 皮亦鸣. 星载-机载混合BiSAR运动误差的分析[J]. 测绘学报, 2008, 37(2): 163-167.) |
| [2] | ZHU Daiyin. SAR Signal Based Motion Compensation through Combining PGA and 2-D Map Drift[C]//Proceedings of the 2nd Asian-Pacific Conference on Synthetic Aperture Radar, APSAR 2009. Shanxi: IEEE, 2009:435-438. |
| [3] | CACCIAMANO A, GIUSTI E, CAPRIA A, et al. Contrast-optimization-based Range-profile Autofocus for Polarimetric Stepped-frequency Radar[J]. IEEE Transactions on Geoscience and Remote Sensing, 2010, 48(4): 2049-2056. |
| [4] | WANG Ling, ZHU Daiyin, ZHU Zhaoda. Improvements of ROPE in ISAR Motion Compensation[C]//Proceedings of the 1st Asian-Pacific Conference on Synthetic Aperture Radar, APSAR 2007. Huangshan: IEEE, 2007:735-738. |
| [5] | WAHL D E, EICHEL P H, GHIGLIA D C, et al. Phase Gradient Autofocus—a Robust Tool for High Resolution SAR Phase Correction[J]. IEEE Transactions on Aerospace and Electronic Systems, 1994, 30(3): 827-834. |
| [6] | CHAN H L, YEO T S. Noniterative Quality Phase-gradient Autofocus (QPGA) Algorithm for Spotlight SAR Imagery[J]. IEEE Transactions on Geoscience and Remote Sensing, 1998, 36(5): 1531-1539. |
| [7] | DENG Yuan, ZHANG Yunhua. Improved PGA Algorithm Based on Adaptive Range Bins Selection[C]// International Conference on Image Analysis and Signal Processing, IASP 2010. Zhejiang: IEEE, 2010: 232-235. |
| [8] | JAKOWATZ C V, WAHL D E. Eigenvector Method for Maximum-likelihood Estimation of Phase Errors in Synthetic-aperture-radar Imagery[J]. Journal of the Optical Society of America A: Optics, Image Science, and Vision, 1993, 10(12): 2539-2546. |
| [9] | EICHEL P H, GHIGLIA D C, JAKOWATZ C V. Speckle Processing Method for Synthetic-aperture-radar Phase Correction[J]. Optics Letters, 1989, 14(20): 1-3. |
| [10] | WAHL D E, JAKOWATZ C V, THOMPSON P A, et al. New Approach to Strip-map SAR Autofocus[C]//Digital Signal Processing Workshop. Yosemite National Park: IEEE, 1994:53-56. |
| [11] | EICHEL P H, GHIGLIA D C, JAKOWATZ C V. Phase Gradient Algorithm as an Optimal Estimator of the Phase Derivative[J]. Optics Letters, 1989, 14(20): 1101-1103. |
| [12] | CHEN Qi, LI Jingwen. Performance Analysis and Improvement of Phase Gradient Autofocus Algorithm[J]. Journal of Beijing University of Aeronautics and Astronautics, 2004, 30(2): 131-134. (陈琦, 李景文. 相位梯度自聚焦算法的性能分析及改进[J]. 北京航空航天大学学报, 2004, 30(2): 131-134.) |
| [13] | YADIN E. SAR Autofocusing Viewed as Adaptive Beamforming on Prominent Scatterers [C]//Record of the 1994 IEEE National Radar Conference. Atlanta: IEEE, 1994:138-143. |
| [14] | CHIANG Chengyen, CHEN Kunshan, WANG Chihtien, et al. Feature Enhancement of Stripmap-mode SAR Images Based on an Optimization Scheme[J]. IEEE Geoscience and Remote Sensing Letters, 2009, 6(4): 870-874. |
| [15] | LAMBERS M, NIES H, KOLB A. Interactive Dynamic Range Reduction for SAR Images[J]. IEEE Geoscience and Remote Sensing Letters, 2008, 5(3): 507-511. |