| 基于8点法的等值线图自动绘制方法 |
等值线的追踪是对离散数据用数学方法插值,将具有相同量值的点变换成图的过程,它将三维信息显示于二维平面,是进行地理要素空间特征分析的强大工具,通过绘制相应的等值线图简单而直观地进行综合分析[1]。现有的等值线追踪算法在进行出口判断时,会依据最近原则进行出口选择,该原则既能保证追踪算法的顺利运行又能保证算法效率最优[2, 3]。
国内外现有的等值线追踪包括:格网线性内插[4]和高次曲面内插[5]。其中,格网线性内插法又分为三角网格法[6-8]和矩形网格法,两者都是通过网格边实现线性内插,再将得到的等值点进行追踪生成等值线[9]。
高次曲面内插分为局部曲面和整体曲面内插[10]。高次曲面内插法的空间变量坐标不易匹配特定的函数表达式,故编程程序复杂且曲面难以契合空间实体[11-13]。
格网线性内插法和高次曲面内插法都是在格网建好后,在格网边上内插等值点进行等值线追踪[14],但是当4条边都存在等值点时,就会出现追踪出口的二义性问题,而现有的常规追踪算法和单个网格内部的改进算法[15]都无法正确寻找到出口。从而导致在山谷与山脊同时出现的混合地貌下,例如马鞍面地貌,会出现与真实情况严重不符的整体地貌被割裂的错误现象。尤其是在地势凹凸走向非常明显,或者插值网格较粗且取值间距较大的情况下,更容易导致异常凸起或凹陷的等值线小圆出现。
针对现有理论方法上存在的不足,本文提出一种基于8点法的等值线追踪算法,通过外向扩张来探索整体地势的走向,由此选择出正确的等值线追踪出口,避免了整体地貌割裂的错误现象,最终使得等值线可以符合并还原原始真实地貌。
1 构建网格区域本文的8点追踪方法,首先需要根据等值点构建规则网格区域。
遍历所有的样本点数据,根据每个样本点在网格区域中的坐标和样本数据的位置、网格距,得出样本点在网格区域中的坐标编号,使用行遍历模式,根据式(1)计算所有节点的插值[16]。
| $ u = \sum\limits_{i = 1}^n {{a_i}} {u_i} $ | (1) |
式中,n表示样本的个数;ai为距离加权;ui为样本值。距离权重为网格点到样本点距离平方的倒数,设di为距离,则权重系数为[16]:
| $ {a_i} = \frac{{{{\left( {1/{d_i}} \right)}^2}}}{{\sum\limits_{i = 1}^n {{{\left( {1/{d_i}} \right)}^2}} }} $ | (2) |
然后,利用8点追踪方法在构建好的规则网格中进行等值线追踪,计算两个格网点中间是否有等值点。设追踪值为Z0,则m、n两点之间等值点存在的判断公式为:
| $ \left( {{Z_m} - {Z_0}} \right)\left( {{Z_n} - {Z_0}} \right) \le 0 $ | (3) |
等值线追踪进入网格后,只能从网格的另外3个边方向追踪出去。如果不在算法上给予处理,就会出现等值线的交叉和不确定现象,如图 1所示。
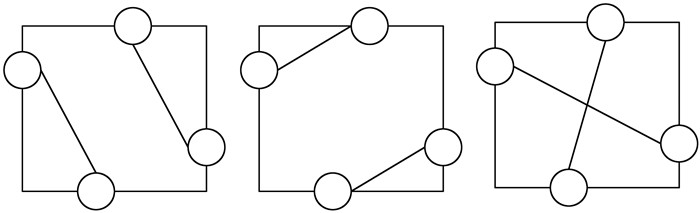 |
| 图 1 等值线的交叉和不确定现象 Fig.1 Contour Crossing and Uncertainty |
现有的研究技术或文献中的解决方案为:假设前一等值点为a1,当前等值点为a2,要追踪的下一等值点为a3,显然可能出现3种情况(a31、a32、a33),如图 2所示,而实际追踪时只能选择一种。则选择的次序为:
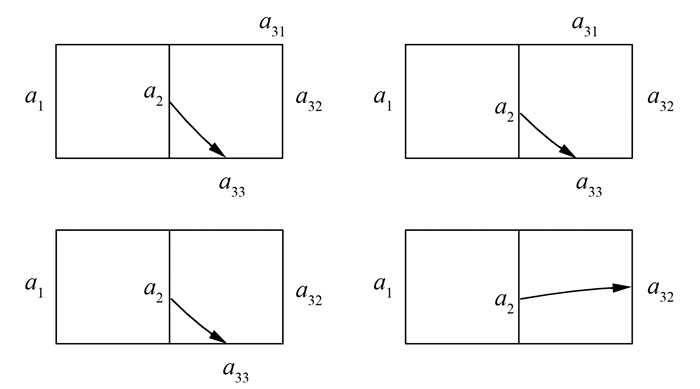 |
| 图 2 现有的追踪方案 Fig.2 Existing Tracking Solution |
1) 当a31、a33都存在时,选择靠近网格左侧边者为a3;
2) 当a31、a33靠近左侧边距离相等时,则选择与a2距离近者为a3;
3) 当a31、a33只有一个存在时,存在点作为a3;
4) 当a31、a33都不存在时,对边必存在a32作为a3。
但是该方法会存在错误,如图 3所示。
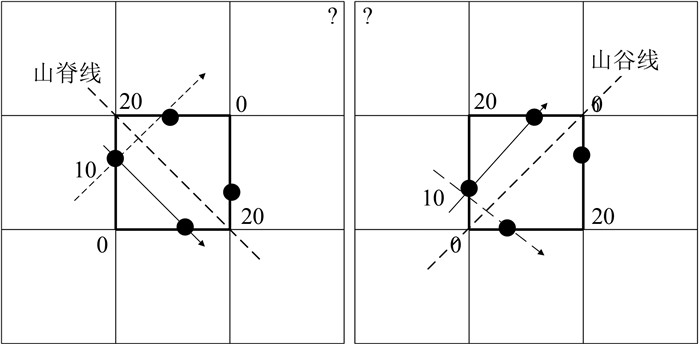 |
| 图 3 现有的追踪方案导致的地貌割裂 Fig.3 Landform Fragmentation Caused by Existing Tracking Schemes |
根据最近法则,会形成图 3中虚线箭头指向的等值线(正确形式应该为图 3中实线箭头),而该等值线将跨越山脊、山谷线,从而导致地貌割裂现象,等值线绘制结果不符合地貌特征。
2.2 基于8点法的等值线追踪算法如图 4所示,以从左边进入为例,中心格的角上的点称为内4点,●表示高于当前高程称为高程点,○表示低于当前高程称为低程点,图形上面c-1、c、c+1、c+2是列号,左面r-1、r、r+1、r+2是行号。
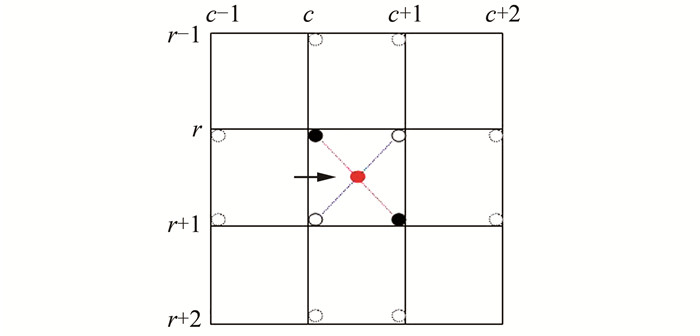 |
| 图 4 8点法追踪 Fig.4 Eight-Point Tracking Method |
除中心格4个顶点外,还应该考虑虚线圆标出的8个点(外8点),判断属于哪种情况。用Hi, j表示i行j列点的高程,算法流程如下:
1) 当外8点的平均高程大于中心格4角中的黑点(即高程点平均值)时,即H外>(1/2)(Hr, c+Hr+1, c+1),应认为是山谷。而当外8点的平均高程小于白点即中心格4角中的低程点平均值时,即H外 < (1/2)(Hr+1, c+Hr, c+1)时,应认为是山脊。按照等值线不穿过山谷、山脊规则即可判断出口。
2) 当H外介于两者之间,即外8点的平均高程大于内4点中低程点平均值,且小于内4点中高程点的平均值时,可认为中心格类似马鞍面。仍然用前高程值与中心点比较的方法,用待定系数法可知,中心点表达式为:
| $ \begin{array}{*{20}{c}} {{H_中心} = A \times \left( {{H_{r, c}} + {H_{r + 1, c}} + 1 + {H_{r + 1, c}} + } \right.}\\ {\left. {{H_{r, c + 1}}} \right)/4 + B \times {H_外}} \end{array} $ | (4) |
3) 要满足两高程点连接的对角线所示条件,由图 4可知,必有:
若
| $ \begin{array}{*{20}{c}} {\left( {{H_{\rm{外}}} = (1/2)\left( {{H_{r, c}} + {H_{r + 1, c + 1}}} \right), } \right.}\\ {{H_中心} = \left( {{H_{r + 1, c}} + {H_{r, c + 1}}} \right)/2} \end{array} $ | (5) |
若
| $ \begin{array}{*{20}{c}} {\left( {{H_{\rm{外}}} = (1/2)\left( {{H_{r + 1, c}} + {H_{r, c + 1}}} \right), } \right.}\\ {{H_{\rm{中心}}} = \left( {{H_{r, c}} + {H_{r + 1, c + 1}}} \right)/2} \end{array} $ | (6) |
4) 将式(5)、式(6)代入式(4)得A=2, B=-1,最后将A、B代入式(4)得:
| $ \begin{array}{*{20}{c}} {{H_{\rm{中心}}} = 2 \times \left( {{H_{r, c}} + {H_{r + 1, c + 1}} + {H_{r + 1, c}} + } \right.}\\ {\left. {{H_{r, c + 1}}} \right)/4 - {H_{\rm{外}}} = 2{H_{\rm{内}}} - {H_{\rm{外}}}} \end{array} $ | (7) |
式中,H内表示内4点的平均高程。
5) 求出H中心后,可与当前高程比较,若当前高程大于H中心,应向左转;若当前高程小于H中心,应向右转。
3 验证与对比为了验证本文的8点法等值线绘制方法,使用文献[16]中涉及的位于中国第一、二阶梯过渡段四川省大渡河流域的数字高程模型数据作为实验数据,当地地形地貌复杂、山高谷深、河网密布,并同时具有丘陵、平坝、沟谷等特征,是理想的实验区域。使用常规等值线追踪方法,绘制的高程值1 800 m等值线如图 5所示。
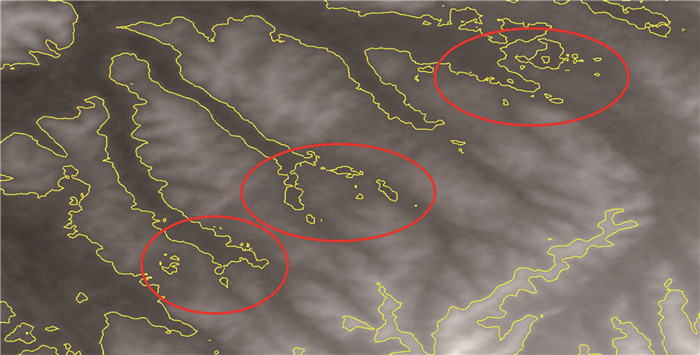 |
| 图 5 常规等值线追踪 Fig.5 Regular Contour Tracking |
从图 5中圈出的部分可以看出,等值线受当地地貌连续起伏影响,会形成割裂原始真实地貌的“等值线小圈”现象,且无法绘制出当前整个流域的地形走势,其根本原因即等值线追踪时以最近距离为闭合依据所导致。对比图 6,在采用本文的8点法等值线追踪算法后,整个流域的整体地貌得到了较好的还原。
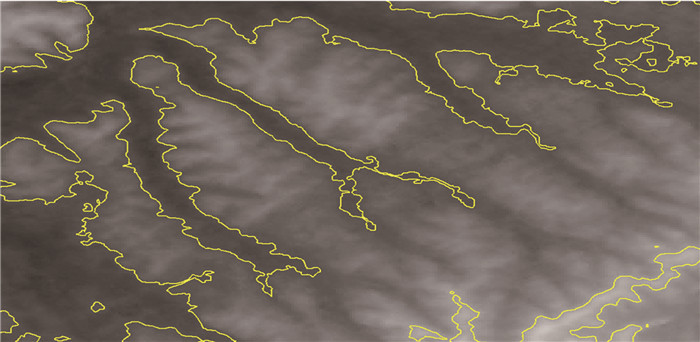 |
| 图 6 基于8点法的等值线追踪 Fig.6 Contour Tracking Based on Eight-Point Method |
4 结束语
本文融入了现实中的地貌特征影响因素,在等值线遇到出口选择情况时,进行了8点法扩张判断,在判断出当前区域地貌特征后,再进行追踪的出口取舍。从而避免了等值线追踪到错误出口,使得等值线不割裂整体地貌,不在山谷、山脊地区出现错误小圆,最终等值线可还原真实地貌特征,绘制的等值线图更利于简单而直观地进行综合分析。在水文模型的建立、地形模拟、公路铁路勘测和规划、自然资源管理等地学领域得到了广泛应用,而且显示出了许多优越性,本算法简单明了,便于用计算机进行处理,能够很容易地计算等高线、坡向坡度,自动提取地形。
| [1] |
李艳茹. 基于规则网格数据的等值线的提取[D]. 呼和浩特: 内蒙古大学, 2010
|
| [2] |
刘静玮. 三角网格等值线的追踪与填充[J]. 电脑与电信, 2013(6): 66-69. DOI:10.3969/j.issn.1008-6609.2013.06.041 |
| [3] |
李强, 李超, 甘建红. 基于三角网的等值线填充算法研究[J]. 计算机工程与应用, 2013, 49(5): 185-189. DOI:10.3778/j.issn.1002-8331.1203-0485 |
| [4] |
沈占锋, 夏列钢, 程熙, 等. 等值线追踪生成等值面过程中的算法策略[J]. 武汉大学学报·信息科学版, 2015, 40(9): 1201-1 208. |
| [5] |
Bao F X, Yao X X, Sun Q H, et al. Smooth Fractal Surfaces Derived from Bicubic Rational Fractal Interpolation[J]. Science China(Information Sciences), 2018, 61(9): 099104. DOI:10.1007/s11432-017-9258-5 |
| [6] |
段友祥, 赵琰, 孙歧峰, 等. 一种基于不规则三角网的地层等值线绘制方法[J]. 计算机应用与软件, 2018, 35(4): 249-253. DOI:10.3969/j.issn.1000-386x.2018.04.046 |
| [7] |
邹水龙, 李志鹏, 金文, 等. 等值线绘制中出现局部尖锐畸形的一种解决方法[J]. 南昌大学学报(理科版), 2017, 41(5): 428-432. DOI:10.3969/j.issn.1006-0464.2017.05.005 |
| [8] |
宋仁波. 基于GIS耦合SketchUp技术的三维地层模型绘制方法[J]. 测绘地理信息, 2014, 39(1): 54-56. |
| [9] |
韦美雁, 杜丹蕾. 基于规则网格的等值线的生成研究[J]. 湖南科技学院学报, 2007(4): 39-41. DOI:10.3969/j.issn.1673-2219.2007.04.014 |
| [10] |
丁鸽, 赵若鹏, 卞磊, 等. 基于离群点探测准则和主成分分析的点云平面拟合效果研究[J]. 测绘地理信息, 2017, 42(6): 25-28. |
| [11] |
马士玲, 马骏, 刘志丹. 一种基于节点插入技术的B样条曲线平滑方法[J]. 计算机时代, 2008, 15(12): 8-9. DOI:10.3969/j.issn.1006-8228.2008.12.004 |
| [12] |
安琪. 几种离散数据网格化方法的对比分析[J]. 内蒙古科技与经济, 2001, 20(1): 87-89. DOI:10.3969/j.issn.1007-6921.2001.01.041 |
| [13] |
秦洪岩, 题正义, 李洋. 重复采动地表变形等值线绘制方法[J]. 辽宁工程技术大学学报(自然科学版), 2017, 36(4): 432-436. |
| [14] |
刘萍. 数值计算方法[M]. 北京: 人民邮电出版社, 2002.
|
| [15] |
王俊骄, 陈晴, 张姗姗. 一种基于网格重心的等值线追踪算法[J]. 浙江气象, 2017, 38(4): 38-41. |
| [16] |
姚驰. 降雨量等值线图的自动绘制方法[J]. 测绘科学, 2015, 40(11): 172-176. |
 2021, Vol. 46
2021, Vol. 46

