| 加权动态GM(1,1)模型在高层建筑沉降预测中的应用 |
2. 湘潭大学土木工程与力学学院,湖南 湘潭,411105;
3. 湖南省天宇检测有限公司,湖南 娄底,417000
2. College of Civil Engineering and Mechanic, Xiangtan University, Xiangtan 411105, China;
3. Hunan Tianyu Detection Corporation, Loudi 417000, China
随着科技与建筑行业的快速发展,各类高层建筑如雨后春笋般拔地而起。在施工或运营期间,房屋的倒塌、倾斜、裂缝等事故时有发生,这是由建筑物内部结构受力不均及外界环境作用导致的不均匀沉降的结果。因此,需要研究出可行的方法对建筑物沉降进行准确预测和分析,掌握其变形规律与发展趋势,使人们能够及时采取适当措施和方法减少工程事故带来的安全隐患和经济损失[1]。目前,常用的变形预测分析模型主要包括时间序列模型、灰色系统模型、卡尔曼滤波模型、人工神经网络模型等[2, 3]。GM(1,1)模型是灰色系统模型中最常用的模型之一,因其具有“小样本、贫信息”的独特优势,已被广泛应用于各种变形预测,并取得了较好的预测结果[4-6]。但是传统GM(1,1)模型易受外界环境干扰,导致模型预测精度低、残差大[7]。
原始数据序列加权是提高模型精度的方法之一。周永领等[8]利用权递增因子构建权矩阵,建立了非等间距加权GM(1,1)模型。赵建飞等[9]将权作为原始序列的平滑因子,借助MATLAB自编程序反复实验得出权值大小;赵泽昆等[10]利用时间因素构建权矩阵,建立了时间加权-新陈代谢GM(1,1)模型。以上方法中的权值大小随时间递增,充分考虑了新信息优先原理,在一定程度上提高了模型的精度,但忽略了误差对原始数据可信度的影响,存在一定局限。本文运用相对误差与时间距离[11]相结合的定权方法,对原始数据序列的加权问题进行研究,建立加权GM(1,1)模型。考虑误差对原始数据可信度的影响,首先将相对误差作为影响因子从原始数据中剔除;然后,把时间距离作为缩小系数加到相对误差上,保证距预测点较近的数据具有较高利用率;最后引入新陈代谢思想[12, 13],充分体现新信息优先原理,建立加权动态GM(1,1)模型。本文采用传统模型、加权模型和加权动态模型对某高层建筑沉降监测数据进行对比分析,并利用MATLAB实现程序化建模[14]。
1 传统GM(1,1)模型构建1)构建累加序列。假设有n个非负原始观测数据序列X(0) = (x(0)(1),x(0)(2),···,x(0)(n)),其中,x(0)(k)≥ 0,k = 1,2,···,n。其1-AGO序列X(1)=(x(1)(1),x(1)(2),···,x(1)(n)),有:
| $ x^{(1)}(k)=\sum\limits_{i=1}^{k} x^{(0)}(i), k=1, 2, \cdots, n $ | (1) |
2)构造背景值。令X(1)的邻近均值生成序列为Z(1) = (z(1)(2),z(1)(3),···,z(1)(n)),其中:
| $ z^{(1)}(k)=\frac{1}{2}\left[x^{(1)}(k)+x^{(1)}(k-1)\right], k=2, 3, \cdots, n $ | (2) |
3)建立微分方程。对X(1)建立一阶线性微分方程:
| $ \frac{\mathrm{d} x^{(1)}(t)}{\mathrm{d} t}+a x^{(1)}(t)=b $ | (3) |
式中,a为发展系数,反映x的发展趋势;b为灰作用量,反映数据间的变化关系。
4)求解方程。根据最小二乘法原理,参数â的表达式如下:
| $ \hat{\boldsymbol{a}}=\left[\begin{array}{ll} a & b \end{array}\right]^{\mathrm{T}}=\left(\boldsymbol{B}^{\mathrm{T}} \boldsymbol{B}\right)^{-1} \boldsymbol{B}^{\mathrm{T}} \boldsymbol{Y} $ | (4) |
式中,
将â代入白化微分方程,以x(1)(1)=x(0)(1) 为初值,可得微分方程的解:
| $ \hat{x}^{(1)}(k)=\left(x^{(0)}(1)-\frac{b}{a}\right) \mathrm{e}^{-a(k-1)}+\frac{b}{a} $ | (5) |
5)预测方程。对式(5)进行累减,得到原始序列X(0)的还原式:
| $ \begin{gathered} \hat{x}^{(0)}(k)=\left(1-\mathrm{e}^{a}\right)\left[x^{(0)}(1)-\frac{b}{a}\right] \mathrm{e}^{-a(k-1)}, \\ k=1, 2, \cdots, n \end{gathered} $ | (6) |
原始数据序列中不同时间点的值都应被赋予一个权值,表征其可靠性[15],而传统GM(1,1)模型将原始序列中的数据看作是同等重要的,直接利用其构造累加序列进行建模,势必会对拟合预测结果造成影响,降低模型精度。本文将GM(1,1)模型一次拟合结果求出的相对误差与时间距离结合起来,对原始序列加权,相对误差在一定程度上直接反映外界干扰对模型造成的影响,以此作为误差影响因子从原始数据中剔除;为突出新旧信息的不同等重要性,将时间距离作为缩小系数加到相对误差上,以保证距预测点较近的数据有较高的利用率。
利用传统GM(1,1)模型对原始数据序列进行拟合,得到残差序列ε(0)={ε(1),ε(2),···,ε(n)},相对误差序列
| $ \rho(t)=\left\{\begin{array}{l} 1-\lambda \varDelta^{(0)}(1), t=1 \\ \frac{1-\lambda \varDelta^{(0)}(t)}{d_{t}}, t=2, 3, \cdots, n \end{array}\right. $ | (7) |
式中,λ为影响因子系数,取值如下:
| $ \lambda=\left\{\begin{array}{l} 2, \frac{\varepsilon(k)}{x^{(0)}(k)} \geqslant 0 \\ -2, \frac{\varepsilon(k)}{x^{(0)}(k)}<0 \end{array}\right. $ | (8) |
因为以x(1)(1)=x(0)(1)为初值,所以ρ(1)= 1。
由式(7)和式(8)可得:
| $ x^{(1)}(k)=\sum\limits_{t=1}^{k} \rho(t) x^{(0)}(k) $ | (9) |
将式(9)代入传统模型,得出最后的还原式:
| $ \begin{gathered} \hat{x}^{(0)}(k)=\frac{1}{\rho(t)}\left(1-\mathrm{e}^{a}\right)\left[x^{(0)}(1)-\frac{b}{a}\right] \mathrm{e}^{-a(k-1)}, \\ t=1, 2, \cdots, n \end{gathered} $ | (10) |
新信息对认知的作用大于老信息[16],为体现新信息优先原理,建立加权动态GM(1,1)模型[17]。利用加权模型求出n + 1时刻的预测值,保持模型维度不变,将x(0)(n + 1)加入原始序列,去掉x(0)(1),组成新原始序列{x(0)(2),x(0)(3),···,x(0)(n + 1)},利用该序列重新建模并预测n + 2时刻的预测值,如此往复。
2.3 精度检验为检验所建模型的可靠性,需要对其进行精度检验,常用的精度检验方法有残差检验合格模型、均方差比合格模型和小误差概率合格模型。
1)残差检验合格模型。设原始序列X(0) = {x(0)(1),x(0)(2),···,x(0)(n)},相应的模拟序列
| $ \varDelta_{k}=\left\{\left|\frac{\varepsilon(1)}{x^{(0)}(1)}\right|, \left|\frac{\varepsilon(2)}{x^{(0)}(2)}\right|, \cdots, \left|\frac{\varepsilon(n)}{x^{(0)}(n)}\right|\right\} $ | (11) |
称
2)均方差比合格模型和小误差概率合格模型。原始数据均值
| 表 1 精度检验等级 Tab.1 Accuracy Test Grades |
 |
3 工程实例分析
本文以湖南省邵阳市某高层建筑房屋沉降监测点实测数据为例,选取2018-11-02—2019-03-22房屋在建过程中具有代表性的监测点P7-1的15期监测数据进行分析,原始数据为5.36、6.02、7.14、8.15、8.30、9.56、9.51、9.81、9.88、10.31、10.64、10.69、10.98、11.25、11.65,代表监测点累计沉降量,单位:mm。选取前10期数据进行建模,后5期数据分别进行3、4、5期预测,建立传统模型、加权模型和加权动态模型,进行对比分析,3期预测的拟合预测结果见表 2。
| 表 2 监测点3期拟合或预测结果 Tab.2 Fitting or Prediction Results of Monitoring Points in Phase 3 |
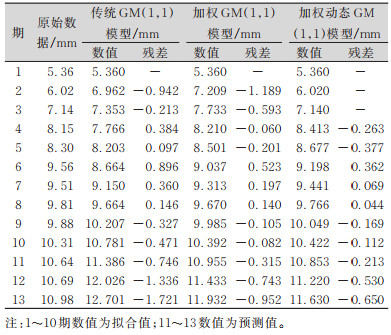 |
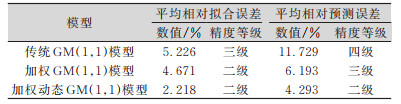
采用残差检验合格模型对拟合预测结果进行精度评定,结果见表 3。由表 3可知,与传统GM(1,1)模型相比,加权动态GM(1,1)模型的拟合与预测精度均有较大提高,预测精度尤为突出,由四级提高到二级。为了更直观地体现房屋沉降趋势和各模型的拟合预测效果,本文绘制了图 1和图 2所示的变形分析曲线。
| 表 3 监测点3期拟合预测精度评定结果 Tab.3 Fitting or Prediction Accuracy Assessment of Monitoring Points in Phase 3 |
 |
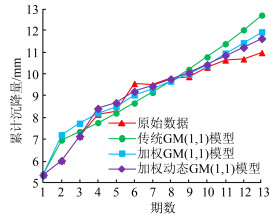 |
| 图 1 监测点3期拟合或预测值 Fig.1 Fitting or Prediction Values of Monitoring Points in Phase 3 |
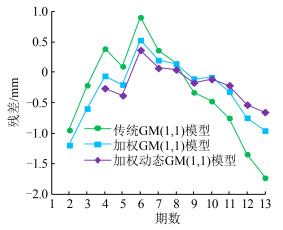 |
| 图 2 监测点3期拟合或预测残差值 Fig.2 Fitting or Prediction Residual Values of Monitoring Points in Phase 3 |
从图 1和图 2可以看出,加权动态GM(1,1)模型的拟合预测曲线与原始数据曲线最为接近,残差分布集中且绝对值较小,残差最大值由传统模型的-1.721 mm减小到-0.650 mm,在原始数据序列波动较大的情况下也能取得较好的拟合预测精度。为检验模型的预测能力,本文采用相同方法进行4期、5期预测,其精度评定结果见表 4。
| 表 4 监测点4期、5期拟合预测精度评定 Tab.4 Evaluation of Fitting or Prediction Accuracy of Monitoring Points in 4 and 5 Phases |
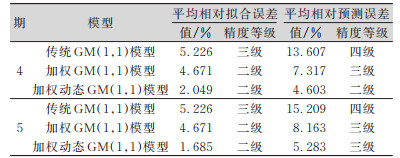 |
分析表 4可得,随着预测期数增加,传统GM(1,1)模型与加权GM(1,1)模型的拟合精度不变,加权动态GM(1,1)模型的拟合精度逐渐提高,这是新信息对认知的作用大于老信息的结果,也是动态模型的优势;3种模型的预测精度都随预测期数的增加而降低,但加权模型降低的速率明显小于传统模型,5期预测的加权动态GM(1,1)模型的平均相对预测误差只有5.283%,达到三级预测精度。对比分析发现,加权动态GM(1,1)模型精度最高,能较好地拟合预测高层建筑沉降数据,客观地反映其沉降变形规律。
4 结束语针对原始数据序列加权问题,本文用相对误差与时间距离相结合的定权方法建立加权动态GM(1,1)模型。将相对误差视为误差影响因子从原始数据中剔除,将距初始值的时间距离作为缩小系数加到相对误差上,保证了新信息具有较高的利用率。结合工程实例分析,发现该模型能有效减小观测数据中的随机误差,对于多期预测均具有较高的拟合预测精度,对高层建筑沉降预测具有一定的参考与应用价值。
相对误差在一定程度上反映了外界环境的影响,时间距离体现出新旧信息的不同等重要性,如何将两者更好结合以提高模型精度有待进一步研究。
| [1] |
陈伟清. 灰色预测在建筑物沉降变形分析中的应用[J]. 测绘科学, 2005, 30(5): 43-45. DOI:10.3771/j.issn.1009-2307.2005.05.014 |
| [2] |
甘祥前, 任超, 刘林波. 基于小波去噪的非等间距多点灰色预测模型[J]. 测绘地理信息, 2018, 43(3): 41-44. |
| [3] |
容静, 文鸿雁, 周吕. 一种改进灰色预测模型在变形预测中的应用[J]. 测绘科学, 2017, 42(3): 35-38. |
| [4] |
Ye J, Dang Y G, Li B J. Grey-Markov Prediction Model Based on Background Value Optimization and Central-Point Triangular Whitenization Weight Function[J]. Communications in Nonlinear Science and Numerical Simulation, 2018, 54: 320-330. DOI:10.1016/j.cnsns.2017.06.004 |
| [5] |
Madhi M H, Mohamed N. An Improved GM(1, 1) Model Based on Modified Background Value[J]. Information Technology Journal, 2016, 16(1): 11-16. DOI:10.3923/itj.2017.11.16 |
| [6] |
郑坚, 陈斌. 基于时间权重序列的GM(1, 1)初始条件优化模型[J]. 控制与决策, 2018, 33(3): 529-534. |
| [7] |
豆红磊, 王景环, 杨静, 等. 基于优化的DGM(1, 1) 在桥梁变形预测中的应用[J]. 工程勘察, 2018, 46(9): 39-43. |
| [8] |
周永领, 黄其欢. 非等间距WGM-AR模型在基坑周边建筑物沉降预测中的应用[J]. 测绘工程, 2014, 23(6): 43-45. DOI:10.3969/j.issn.1006-7949.2014.06.010 |
| [9] |
赵建飞, 张俊中, 李东辉. 加权GM(1.1)模型在地铁沉降监测中的应用[J]. 测绘与空间地理信息, 2015, 38(5): 56-58. DOI:10.3969/j.issn.1672-5867.2015.05.018 |
| [10] |
赵泽昆, 孟尚臻, 酒亚宾, 等. 基于时间加权-新陈代谢GM(1, 1)模型在建筑物沉降预测中的应用[J]. 矿山测量, 2019, 47(1): 24-26. DOI:10.3969/j.issn.1001-358X.2019.01.006 |
| [11] |
马攀, 孟令奎, 文鸿雁. 基于小波分析的Kalman滤波动态变形模型研究[J]. 武汉大学学报·信息科学版, 2004, 29(4): 349-353. |
| [12] |
张朝飞, 罗建军, 徐兵华, 等. 基于灰色理论的新陈代谢自适应多参数预测方法[J]. 上海交通大学学报, 2017, 51(8): 970-976. |
| [13] |
梁永平, 严丽萍. 基于小波消噪的动态灰色桥墩沉降预测模型[J]. 测绘地理信息, 2017, 42(6): 65-68. |
| [14] |
曾波, 尹小勇, 孟伟. 实用灰色预测建模方法及其MATLAB程序实现[M]. 北京: 科学出版社, 2018.
|
| [15] |
吴少华, 程朋根, 胡智仁. 卡尔曼-非等时距加权灰色线性组合模型探讨[J]. 测绘科学, 2016, 41(5): 137-142. |
| [16] |
刘思峰, 杨英杰, 吴利丰, 等. 灰色系统理论及其应用: 第7版[M]. 北京: 科学出版社, 2014.
|
| [17] |
徐旭, 黄声享, 高方强, 等. 基于残差改正的动态非等时距灰色模型及应用[J]. 测绘地理信息, 2015, 40(3): 48-51. |
 2022, Vol. 47
2022, Vol. 47


