| 3维建筑综合算法的两层次评价模型 |
2. 中国电子设备系统工程公司研究所,北京,100141
2. Institute of China Electronic System Engineering Corporation, Beijing 100141, China
与2维居民地综合相比,3维建筑综合中对象结构的变化使综合算法的设计更为多样。单一建筑综合中代表性的算法包括基于面分割的化简方法[1]、基于形态学的化简方法[2]、半空间模型法[3, 4]、三步化简法[5]、空间转换化简法[6]等。针对建筑群综合的典型算法包括基于格式塔理论的方法[7]、基于纹理和建筑底面的合并方法[8]等。由于3维建筑表达方式的多样性和综合算法的复杂性[9],对综合算法进行科学合理的评价较为困难,而合理的评价是用户选择算法和开发者改进算法的基础[10]。
针对这一问题,本文提出了一种概略评价和详细评价相结合的两层次评价模型,该模型兼顾综合算法评价的效率和完善性,能够为综合算法的选择和改进提供支持。
1 3维建筑综合概略评价模型 1.1 概略评价指标概略评价模型的评价指标需具备两个特点:①易于从算法描述中获取;②能够有效反映算法的差别。可采用以下9项指标:算法的处理效率、能否获取连续多细节层次(levels of detail,LoD)模型、是否为单参数控制综合力度、能否处理建筑群、算法的可扩展性、是否支持语义模型、非正交结构处理能力、房顶处理能力、所能处理的LoD层次。
1.2 算法性能评价的量化方法根据评价指标的特点,可分为布尔型指标和层次型指标两类。布尔型指标为评价结果提供是和否两个选项;层次型指标分为若干个不同的层次(层次数通常为3~5,以评价者的经验知识为基础),各层次由低到高排列。
若评价算法对应的n个指标值分别为p1, p2, …, pn,则可由式(1)计算得到以100为最佳基准的算法通用评价结果ER:
| $ {\rm{ER}} = \left( {100 \times \sum\limits_{i = 1}^n {{p_i}} } \right)/n $ | (1) |
针对不同应用对综合要求的差别,在以某一应用为目标评价3维建筑算法整体性能时,可以从效率、形态、位置、外观和应用范围等5个方面出发,根据不同指标对各方面的影响进行赋权。针对特定应用的综合算法整体评价结果WER为:
| $ {\rm{WER}} = \sum\limits_{i = 1}^5 {\left( {{w_i}\left( {\sum\limits_{j = 1}^n {{p_{ji}}} {v_j}} \right)} \right)} $ | (2) |
式中,wi为5个评价方面的影响因子;pji为指标j对于wi的权值;vj为对指标j评价的具体值。其中,
针对4类典型3维建筑综合算法(对应参考文献[1-5],后文采用第一完成人代表算法名称),可采用概略评价模型的9项评价指标对其进行评价,各指标采用相同权值,结果如表 1所示。
| 表 1 3维建筑几种主要综合算法的概略评价 Tab.1 Summary Estimation of Four Main 3D Building Generalization Algorithms[3, 4] |
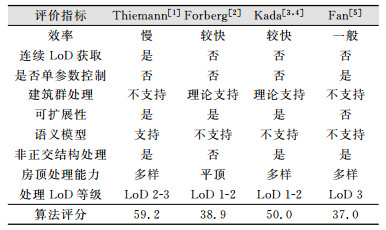 |
由表 1可知,概略评价模型以应用为目标对算法整体能力进行评价,采用的评价指标有限,评价结果不能完全客观地反映算法在某一方面的性能。如Fan算法虽然得分较低,但在处理结构复杂的LoD 3模型的能力出色。针对不同应用,可根据具体需求对指标进行合理赋权后评价。
2 3维建筑综合概略评价模型 2.1 综合中建筑对象的变化3维建筑综合中对象的改变主要体现在几何关系和语义关系方面。几何关系变化主要包括拓扑关系的改变、形态保持不合理和空间位置变化等。语义关系的变化主要体现在综合后建筑的几何模型与语义模型不一致。
2.2 拓扑关系评价3维建筑综合中拓扑关系的改变可以从底面轮廓和建筑整体两个方面进行评价。对于建筑底面轮廓,综合中拓扑关系的变化主要是因为算法对邻近(相接)对象的处理不够完善。拓扑关系错误主要包括拓扑相交错误和底面轮廓由相接变为相离两个方面,如图 1所示。前者往往由化简操作产生,在建筑群的综合中采用合理阈值将其聚合能够很好地解决这一问题;对于后者,需在综合前计算底面轮廓之间的相接关系,判断综合后相接对象的变化情况来确定其拓扑一致性。
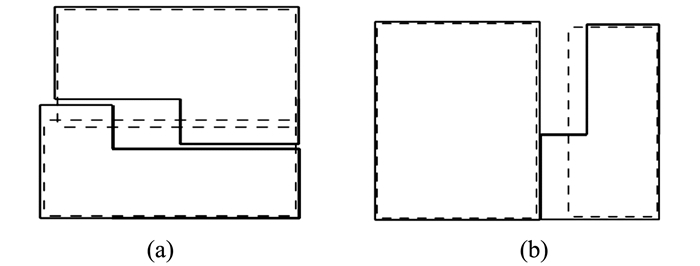 |
| 图 1 建筑底面轮廓综合中出现的拓扑错误 Fig.1 Topological Error of Building Ground Plan in Generalization |
单个建筑综合前后拓扑关系的错误主要表现在综合后建筑表面模型的面缺失和相接面关系的变化等,如图 2所示。建筑表面模型的拓扑完整性采用如下方法表达:对于建筑表面任意构成面的每一条边界线段,若均存在另一条与其重合且方向相反的线段,则认为该对象拓扑完整;否则判断建筑拓扑不完整。对于建筑几何模型缺失的面,只需增加相应面结构使其表面闭合;对于综合后变为不相接的面,需判断面轮廓间的关系,移动位置偏离的面。
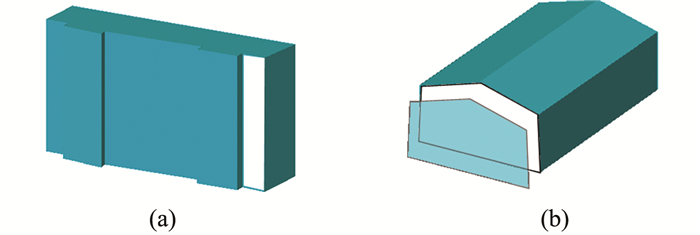 |
| 图 2 综合后建筑模型产生的拓扑不完整现象 Fig.2 Surface Error of Building Caused by Generalization |
2.3 几何精度评价
建筑底面轮廓中心点位置的变化是几何精度评价的直接指标,主要用于整体位移的位置精度评估。建筑3维几何模型中心点高程的变化是度量高度维位置精度变化的重要指标。
建筑原始底面轮廓的部分顶点不位于综合后的底面轮廓上,可通过判断原始轮廓各顶点与综合后轮廓线之间的最大距离,对其位置精度进行度量。该指标称为顶点最大偏移量vdp:
| $ \begin{equation} \mathrm{vdp}=\max (\mathrm{dist}(i)) \quad(i=1, 2, \cdots, m) \end{equation} $ |
式中, dist(i)=min(dist(Gi, PjPj+1)) (j=1, 2, …, n-1),m、n分别为综合前后底面轮廓的顶点数,Gi为综合前轮廓点,PjPj+1为综合后轮廓边界线段。
将该距离扩展到3维空间,可实现对建筑表面模型顶点最大偏移的度量。建筑高程对于某些应用影响较大,综合前后建筑最高点高程的变化也是几何精度评价的重要指标之一。综合前后建筑底面的重合度能够合理地表达轮廓边界的变化。设原始建筑对象底面为G0,综合后建筑底面记为G,则底面重合度S-pos为:
| $ {S_ - }{\rm{pos}} = \frac{{{G_0} \cap G}}{{{G_0} \cup G}} $ | (3) |
式中,0≤S-pos≤1。S-pos值越大,则建筑底面几何精度的变化越小,反之几何精度损失越大。若S-pos=0,则两轮廓不相交;若S-pos=1,则综合未造成建筑底面轮廓变化。建筑对象的整体重合度也可通过类似方法求得。
2.4 几何形态评价正交结构特征是否得以保留是建筑几何形态评价的重要依据。墙面与底面垂直形态保持的评价,可通过对比综合前后墙面累积倾斜度的变化实现。累积倾斜度Incline为:
| $ {\rm{ Incline }} = \sum\limits_{i = 1}^n {\left( {{A_i}|{\rm{ normal}}{{\rm{ }}_i} \times z|} \right)} $ | (4) |
式中,Ai为某一墙面的面积;normali为该面的标准法向量。综合前后累积倾斜度之差越小,则墙面结构保持越好。
将3维建筑表面模型的各面作为有向面,根据三个坐标轴所形成的六个方向计算各方向的面积值,通过对比综合前后各方向面积的变化可实现建筑整体形态保持的评价。若建筑表面模型由n个平面构成,根据式(5)计算出建筑几何表面在各方向上的面积值:
| $ {A_{{\rm{axis}}}} = \sum\limits_{i = 1}^n {{A_i}} {\rm{normai}}{{\rm{l}}_i} \times {\rm{axis }} $ | (5) |
式中, Ai为某一平面的面积;normali为该面的标准法向量; axis为面积的方向。综合前后Ax、Ay、Az的变化反映了建筑在yz、zx、xy三个平面投影轮廓的变化,若Aaxis-A-axis≠0,则说明该方向表面不完整。
建筑方向性的保持建筑底面轮廓在主方向及其垂直方向上长度的变化以及综合前后建筑对象底面面积、周长及建筑表面积、体积的变化都是建筑几何形态评价的重要指标。
3 结束语本文提出了概略模型与详细模型相结合的两层次评价方法,并对几种典型算法进行了概略评价,得出了算法的综合能力和适用范围;针对详细评价模型从理论层面提出详细的评价指标,为算法设计者评价具体算法性能提供基础。该模型为3维建筑综合算法的评价提供了理论支持,但仍存在一些不足,具体表现为:①评价模型的设计以边界表达模型为基础,对其他方式表达的建筑模型考虑较少;②详细评价模型相关指标的完整性和适用性有待进一步验证。后续研究中主要针对以上问题进一步对评价模型进行完善。
| [1] |
Thiemann F, Sester M. Segmentation of Buildings for 3D-Generalisation[C]. ICA Workshop on Generaliz ation and Multiple Representation, Leicester, UK, 2004
|
| [2] |
Forberg A. Generalization of 3D Building Bata Based on a Scale-Space Approach[J]. ISPRS Journal of Photogrammetry and Remote Sensing, 2007, 62(2): 104-111. DOI:10.1016/j.isprsjprs.2007.01.002 |
| [3] |
Kada M.3D Building Generalization Based on Half-Space Modeling[C]. Proceedings of the ISPRS Workshop on Multiple Representation and Interoperability of Spatial Data, Hannover, Germany, 2006
|
| [4] |
Kada M. 3D Building Generalisation by Roof Simplification and Typification[C]. The 23rd International Cartographical Conference, Moscow, Russia, 2007
|
| [5] |
Fan Hongchao, Meng Liqiu. A Three-Step Approach of Simplifying 3D Buildings Modeled by CityGML[J]. International Journal of Geographical Information Science, 2012, 26(6): 1 091-1 107. DOI:10.1080/13658816.2011.625947 |
| [6] |
Ying Shen, Guo Renzhong, Yang Jie, et al. 3D Space Shift from CityGML LoD 3-Based Multiple Building Elements to a 3D Volumetric Object[J]. ISPRS International Journal of Geo-Information, 2017, 6(1). DOI:10.3390/ijqi6010017 |
| [7] |
Yang Ling, Zhang Liqiang, Ma Jingtao, et al. Interactive Visualization of Multi-Resolution Urban Building Models Considering Spatial Cognition[J]. International Journal of Geographical Information Science, 2011, 25(1): 5-24. |
| [8] |
Liu Po, Li Chengming, Li Fei, et al. Texture-Cognition-Based 3D Building Model Generalization[J]. ISPRS International Journal of Geo-Information, 2017, 6: 260. DOI:10.3390/ijgi6090260 |
| [9] |
葛磊, 武芳, 朱强. 3维建筑综合基本方法的探讨[J]. 测绘信息与工程, 2009, 34(2): 15-17. |
| [10] |
郭庆胜. 地图自动综合的广义性和评价标准的研究[J]. 测绘信息与工程, 2000, 25(1): 19-21. DOI:10.3969/j.issn.1007-3817.2000.01.006 |
 2020, Vol. 45
2020, Vol. 45

