| 坐标转换中的角度长度与面积变形定量分析 |
2. 昆明市测绘研究院,云南 昆明, 650051
2. Kunming Surveying and Mapping Institute, Kunming 650051, China
在坐标系转换过程中,重要工程测绘资料,如坐标点成果在转换前后会产生差异。由坐标转换差异带来不同程度的角度变形、长度变形和面积变形对实际测绘生产中具有有不同程度的影响。举例而言,土地确权时,同一块土地采用不同坐标系,其面积往往不同。这种不同固然有测量误差引起的,然而投影变形以及坐标转换同样会带来面积变形,最终影响土地面积。因此,定量分析坐标转换中产生的变形是十分必要的。本文首先对坐标转换进行分类,并定量分析不同类型的坐标转换造成的角度变形、长度变形以及面积变形的影响。
1 坐标变换中变形量推导坐标变换就是从一种坐标形式变换到另一种坐标形式。在同一基准下,对同一个点的描述有不同的表达形式[1]。比如大地坐标系采用大地经度、大地纬度和大地高描述椭球面上的点,而高斯-克吕格投影则是将椭球面上的点投影至有严密数学定义的平面上,采用二维坐标描述相同的点。常见的坐标变换有投影变换以及三维坐标向大地测量坐标系的转换[2-4]。本文将对七参数变换和高斯投影变换的变形量进行理论推导。
1.1 七参数变换 1.1.1 长度变形七参数转换公式为:
| $ \left[ \begin{array}{l} X\prime \\ Y\prime \\ Z\prime \end{array} \right] = \left[ \begin{array}{l} {\rm{ \mathsf{ δ} }}X\\ {\rm{ \mathsf{ δ} }}Y\\ {\rm{ \mathsf{ δ} }}Z \end{array} \right] + \left( {1 + m} \right){\mathit{\boldsymbol{R}}_1}\left( {{\varepsilon _X}} \right){\mathit{\boldsymbol{R}}_2}\left( {{\varepsilon _Y}} \right){\mathit{\boldsymbol{R}}_3}\left( {{\varepsilon _Z}} \right)\left[ \begin{array}{l} X\\ Y\\ Z \end{array} \right] $ | (1) |
式中,m为比例因子;δX、δY、δZ为平移参数;εX、εY、εZ为3个旋转角;R1(εX)、R2(εY)、R3(εZ)为3个旋转角对应的旋转矩阵。若原坐标系下有矢量
| $ ({X_2} - {X_1}, {Y_2} - {Y_1}, {Z_2} - {Z_1}) $ |
经过七参数转换,在目标坐标系下记为矢量
| $ (X{\prime _2} - X{\prime _1}, Y{\prime _2} - Y{\prime _1}, Z{\prime _2} - Z{\prime _1}) $ |
根据七参数转换公式,则
| $ \overrightarrow {A\prime B\prime } = \left( {1 + m} \right){\mathit{\boldsymbol{R}}_1}\left( {{\varepsilon _X}} \right){\mathit{\boldsymbol{R}}_2}\left( {{\varepsilon _Y}} \right){\mathit{\boldsymbol{R}}_3}\left( {{\varepsilon _Z}} \right)\left[ \begin{array}{l} {X_2} - {X_1}\\ {Y_2} - {Y_1}\\ {Z_2} - {Z_1} \end{array} \right] $ | (2) |
其长度为:
| $ \begin{array}{l} \;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\left| {\overrightarrow {A\prime B\prime } } \right| = \\ \left( {1 + m} \right)\left| {{\rm{ }}{\mathit{\boldsymbol{R}}_1}\left( {{\varepsilon _X}} \right)} \right|\left| {{\rm{ }}{\mathit{\boldsymbol{R}}_2}\left( {{\varepsilon _Y}} \right)} \right|\left| {{\rm{ }}{\mathit{\boldsymbol{R}}_3}\left( {{\varepsilon _Z}} \right)} \right|\left| \begin{array}{l} {X_2} - {X_1}\\ {Y_2} - {Y_1}\\ {Z_2} - {Z_1} \end{array} \right| = \\ \;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\left( {1 + m} \right)\left| {\overrightarrow {AB} } \right| \end{array} $ | (3) |
可见,经过其参数转换,长度变为原来的(1+m)倍,与坐标以及平移参数、旋转参数没有关系。
1.1.2 角度变形两个向量
| $ {\rm{cos}}\theta = \frac{{\overrightarrow {AB} {\rm{ }} \cdot \overrightarrow {AC} }}{{\left| {AB} \right|\left| {AC} \right|}} = \frac{a}{{b \cdot c}} $ | (4) |
| $ \begin{array}{l} a = \left( {{X_2} - {X_1}} \right)\left( {{X_3} - {X_1}} \right) + \\ \left( {{Y_2} - {Y_1}} \right)\left( {{Y_3} - {Y_1}} \right) + \left( {{Z_2} - {Z_1}} \right)\left( {{Z_3} - {Z_1}} \right) \end{array} $ | (5) |
| $ b = {\rm{ }}\sqrt {{{\left( {{X_3} - {X_1}} \right)}^2} + {{\left( {{Y_3} - {Y_1}} \right)}^2} + {{\left( {{Z_3} - {Z_1}} \right)}^2}} $ | (6) |
| $ c = \sqrt {{{\left( {{X_2} - {X_1}} \right)}^2} + {{\left( {{Y_2} - {Y_1}} \right)}^2} + {{\left( {{Z_2} - {Z_1}} \right)}^2}} $ | (7) |
经过七参数转换,两个向量
| $ \begin{array}{l} \;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\overrightarrow {A\prime B\prime } {\rm{ }} \cdot \overrightarrow {A\prime C\prime } {\rm{ }} = {\left( {1 + m} \right)^2}\\ {X^{\rm{T}}}\mathit{\boldsymbol{R}}_3^{\rm{T}}\left( {{\varepsilon _Z}} \right)\mathit{\boldsymbol{R}}_2^{\rm{T}}\left( {{\varepsilon _Y}} \right)\mathit{\boldsymbol{R}}_1^{\rm{T}}\left( {{\varepsilon _X}} \right){\mathit{\boldsymbol{R}}_1}\left( {{\varepsilon _X}} \right){\mathit{\boldsymbol{R}}_2}\left( {{\varepsilon _Y}} \right){\mathit{\boldsymbol{R}}_3}\left( {{\varepsilon _Z}} \right)X \end{array} $ | (8) |
其中,
| $ X = \left[ \begin{array}{l} {X_2} - {X_1}\\ {Y_2} - {Y_1}\\ {Z_2} - {Z_1} \end{array} \right] $ | (9) |
因为R1T(εX)R1(εX)=E,R2T(εX)R2(εX)=E,R3T(εX)R3(εX)=E, 因此可以得到
| $ \overrightarrow {A\prime B\prime } {\rm{ }} \cdot \overrightarrow {A\prime C\prime } = {\left( {1 + m} \right)^2}\overrightarrow {AB} {\rm{ }} \cdot \overrightarrow {AC} $ | (10) |
又因为
| $ {\rm{cos}}\theta \prime = \frac{{\overrightarrow {A\prime B\prime } \cdot \overrightarrow {A\prime C\prime } }}{{\left| {A\prime B\prime } \right|\left| {A\prime C\prime } \right|}} = \frac{{\overrightarrow {AB} \cdot \overrightarrow {AC} }}{{\left| {AB} \right|\left| {AC} \right|}} $ | (11) |
可见,七参数转换前后,向量夹角角度不变。
1.1.3 面积变形任意空间曲面经过无穷分割以后,都可以分割为无穷多个微分曲面。微分曲面,其面积近似等于平面面积。用数学公式表达为:
| $ A = \iint\limits_{{D_{xy}}} {\frac{1}{{{\text{cos}}\gamma }}{\text{d}}x{\text{d}}y} $ | (12) |
式中,γ为分割后的微分曲面与xoy平面的夹角;dxdy为微小曲面在xoy平面的投影面积。很显然,进行七参数转换以后,空间曲面的面积变为:
| $ A\prime = \iint\limits_{{D_{x\prime y\prime }}} {\frac{1}{{{\text{cos}}\gamma }}dx\prime dy\prime } = {\left( {1 + m} \right)^2}\iint\limits_{{D_{xy}}} {\frac{1}{{{\text{cos}}\gamma }}{\text{d}}x{\text{d}}y} $ | (13) |
也就是说,空间曲面面积为原坐标系下的(1+m)2倍。将平方项展开并忽略二阶小项,任意多边形面积变为(1+2m)倍,既面积变形为2m。
1.2 投影变换 1.2.1 长度变形中国采用高斯-克吕格平面坐标系作为法定坐标系,因此,坐标成果必须投影至高斯平面上[5, 6]。本节定量分析由于高斯投影产生的变形量。
设有微分矢量
| $ N = {\text{ }}\frac{a}{W}, W = \sqrt {{\text{1}} - {e^2}{\text{si}}{{\text{n}}^2}{B_m}} $ | (14) |
将其改化至椭球面上,长度变为
| $ {D_e} = D\left( {1 - \frac{{{H_m}}}{{{N_m}}} + \frac{{{H_m}^2}}{{{N_m}^2}}} \right) $ | (15) |
设其投影至高斯平面上的点坐标为Ae和Be将椭球面上微分矢量
| $ {D_p} = {D_e}\left( {1 + \frac{{{y_m}}}{{2{N_m}}} + \frac{{\Delta {y^2}}}{{24{N_m}^2}}} \right) $ | (16) |
因此,高斯平面上微分矢量的长度与三维空间坐标系下的长度关系为:
| $ \begin{array}{l} \;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;{D_p} = \\ D\left( {1 - \frac{{{H_m}}}{{{N_m}}} + \frac{{{H_m}^2}}{{{N_m}^2}}} \right)\left( {1 + \frac{{{y_m}}}{{2{N_m}}} + \frac{{\Delta {y^2}}}{{24{N_m}^2}}} \right) \end{array} $ | (17) |
忽略三阶以上小量,可得
| $ {D_p} = D\left( {1 - \frac{{{H_m}}}{{{N_m}}} + \frac{{{y_m}^2}}{{2{N_m}^2}}} \right) $ | (18) |
即投影导致的长度变形量ΔD为:
| $ \Delta D = - \frac{{{H_m}}}{{{N_m}}} + \frac{{{y_m}^2}}{{2{N_m}^2}} $ | (19) |
式(19)表明,在高斯-克吕格投影下,投影长度变形与微分矢量的高程呈负相关,与微分矢量至中央子午线的距离的平方成正相关。
1.2.2 面积变形椭球面上的微分梯形由两条微分经线纬线相交形成[7],如图 1所示。
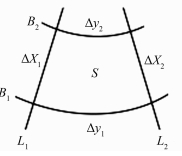 |
| 图 1 椭球微分梯形 Fig.1 Ellipsoidal Differential Trapezoid |
由图 1可知,微分面积dS等于坐标微分长度dx和dy的乘积:
| $ {\rm{d}}S = {\rm{d}}x \times {\rm{d}}y $ | (20) |
已知
| $ {\rm{d}}x = M{\rm{d}}B $ | (21) |
| $ {\rm{d}}y = N{\rm{cos}}B{\rm{d}}L $ | (22) |
于是微分梯形面积可以表示为:
| $ \begin{array}{l} {\rm{d}}S = MN{\rm{d}}B{\rm{d}}L = \frac{{{a^2}(1 - {e^2}){\rm{cos}}B}}{{{W^4}}}{\rm{d}}B{\rm{d}}L = \\ \;\;\;\;\;\;\;\;\;\;\;\;\;\;\frac{{{b^2}cosB}}{{{{(1 - {e^2}{\rm{si}}{{\rm{n}}^2}B)}^2}}}{\rm{d}}B{\rm{d}}L \end{array} $ | (23) |
则有
| $ S = {b^2}\mathop {\iint\limits_{{L_1}{B_1}} {}}\limits^{{L_2}{B_2}} {(1 - {e^2}{\text{si}}{{\text{n}}^2}B)^{ - 2}}{\text{cos}}B{\text{d}}B{\text{d}}L $ | (24) |
可得:
| $ S = {b^2}\left( {{L_2} - {L_1}} \right)\int\limits_{{B_1}}^{{B_2}} {{{(1 - {e^2}{\rm{si}}{{\rm{n}}^2}B)}^{ - 2}}{\rm{cos}}B{\rm{d}}B} $ | (25) |
将式(25)级数展开得:
| $ \begin{array}{l} S = {b^2}\left( {{L_2} - {L_1}} \right)\int\limits_{{B_1}}^{{B_2}} {({\rm{cos}}B + 2{e^2}{\rm{si}}{{\rm{n}}^2}B{\rm{cos}}B + } \\ 3{e^4}{\rm{si}}{{\rm{n}}^4}B{\rm{cos}}B + 4{e^6}{\rm{si}}{{\rm{n}}^6}B{\rm{cos}}B + \cdots ){\rm{d}}B \end{array} $ | (26) |
积分后得:
| $ \begin{array}{l} S = {b^2}({L_2} - {L_1})|{\rm{sin}}B + {\rm{ }}\frac{2}{3}{e^2}{\rm{si}}{{\rm{n}}^3}B + \\ \;\;\;\;\;\;\frac{3}{5}{e^4}{\rm{si}}{{\rm{n}}^5}B + \frac{4}{7}{e^6}{\rm{si}}{{\rm{n}}^7}B + \cdots |_{{B_1}}^{{B_2}} \end{array} $ | (27) |
通过将椭球面上梯形图幅的边线交点的大地坐标按高斯投影原理投影到高斯直角平面坐标上,依次将高斯平面上的投影点连接成一个封闭的图形,这个封闭图形的面积就是椭球面梯形图幅在高斯平面上的投影图幅面积,如图 2所示。
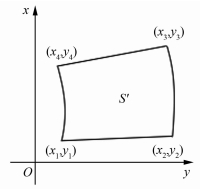 |
| 图 2 高斯投影梯形 Fig.2 Gaussian Projection Trapezoid |
通过解析法可得面积计算公式如下:
| $ \begin{array}{l} \;\;S\prime = \frac{1}{2}\left[ {\left( {{x_1} + {x_2}} \right)\left( {{y_2} - {y_1}} \right) + \left( {{x_2} + {x_3}} \right)\left( {{y_3} - } \right.} \right.\\ \left. {\left. {{y_4}} \right) + \left( {{x_3} + {x_4}} \right)\left( {{y_4} - {y_3}} \right) + \left( {{x_4} + {x_1}} \right)\left( {{y_1} - {y_4}} \right)} \right] \end{array} $ | (28) |
推广到n点公式为:
| $ \left\{ \begin{array}{c} S\prime = \frac{1}{2}\left| {\sum\limits_{i = 1}^n {{x_i}\left( {{y_{i + 1}} - {y_{i - 1}}} \right)} } \right|\\ 或\\ S\prime = \frac{1}{2}\left| {\sum\limits_{i = 1}^n {{y_i}\left( {{x_{i + 1}} - {x_{i - 1}}} \right)} } \right| \end{array} \right. $ | (29) |
当i=1时,i-1取n;当i=n时,i+1取1。计算时点号应从左上角以1开始顺时钟方向依序顺编。
故高斯投影后图幅面积变形为:
| $ {\rm{V}} = \frac{{{\rm{d}}S\prime }}{{{\rm{d}}S}} - 1 $ | (30) |
在七参数转换中取尺度因子为10×10-6,X、Y、Z 3个方向的旋转角均为10″,3个方向平移量均为100 m。原始数据是X、Y、Z 3个坐标均采用随机数生成的10个离散点,相互组合成三角形,通过七参数坐标转换后对三角形中的角度、边长和面积变形进行统计[8-14],统计结果分别如表 1、表 2和表 3所示。
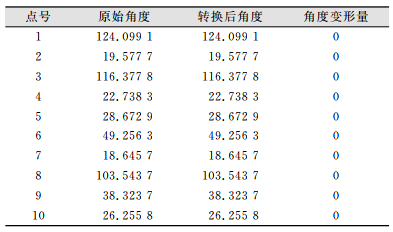
| 表 1 角度变形统计表/(°) Tab.1 Statistical of Angular Deformation/(°) |
 |
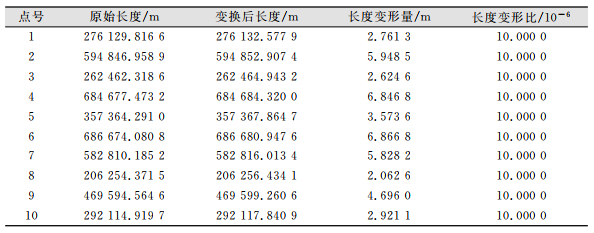
| 表 2 长度变形统计表 Tab.2 Statistics of Length Deformation |
 |
| 表 3 面积变形统计表 Tab.3 Statistics of Area Deformation |
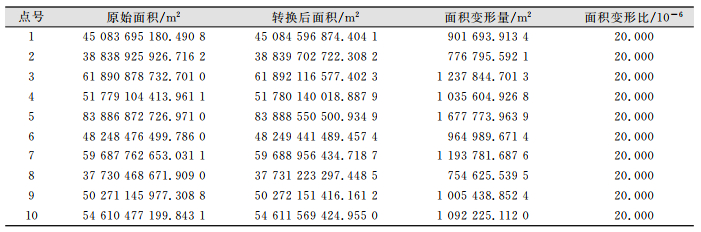 |
从表 1、表 2、表 3可以看出七参数转换中,当尺度因子m=10×10-6时角度不发生变形,长度变形为10×10-6即为m,面积变形为20×10-6即为2m。
在高斯面积投影实验中,分别进行经度链方向和纬度链方向的变形实验,在进行经度链方向投影变形中,本文选取中央子午线为111°,沿纬线方向选择经差为3′45″、纬差为2′30″的椭球面格网进行高斯投影面积对比,投影结果如图 3所示;在进行纬度链方向投影变形中,沿经线方向选取了经差为3′45″、纬差为1°的椭球面格网进行不同纬度的高斯面积投影计算,投影结果如图 4所示。
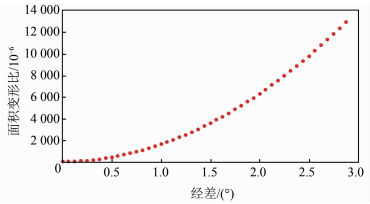 |
| 图 3 经度链高斯投影变形 Fig.3 Gaussian Projection Deformation of Longitude Chain |
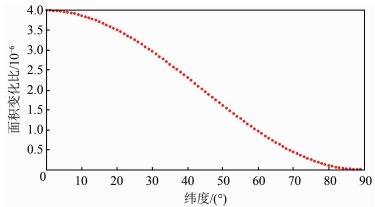 |
| 图 4 纬度链高斯投影变形 Fig.4 Gaussian Projection Deformation of Latitude Chain |
从图 3和图 4中可以得知,图斑椭球的高斯投影的面积变形随着距离中央经线的距离增大而增大,在6°带最大变形比可达13 000×10-6。高斯投影面积变形比随着纬度的增大而减小,面积变形的变化率先增大后减小,在纬度为44°~45°带面积变形变化率达到最大值。
在高斯投影长度变形中,选取平均高程Hm在-160~300 m,Ym在-50~50 km之间的数据进行长度变形分析,结果如图 5所示。
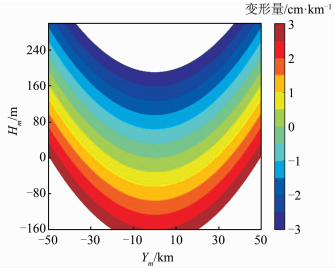 |
| 图 5 高斯投影长度变形 Fig.5 Gaussian Projection Length Deformation |
从图 5中可以看出,当Hm值为负且不小于-160 km时,其投影变形均不会超出2.5 cm/km的限差;当Hm值为正的情况下,距离中央子午线越近时,投影变形越小。
3 结束语本文通过推导七参数的角度、长度和面积变形公式,及图斑椭球面积公式和高斯投影面积计算公式,对坐标变化中的角度、长度和面积变形进行定量分析,并通过模拟坐标变换对推导结果进行验证,得到以下结论:
1) 七参数变换中角度不发生变形;
2) 七参数变换中长度变形为m,与坐标以及平移参数、旋转参数没有关系,其中m为七参数转换中的比例因子;
3) 七参数变换中面积变形为2m,与坐标以及平移参数、旋转参数没有关系,其中m为七参数转换中的比例因子;
4) 高斯投影变换的面积变形比随着图斑距离中央子午线的距离增大而增大,最大可以达到13 000×10-6;
5) 高斯投影变换面积变形比随着纬度的增大而减小,面积变形的变化率先增大后减小,在纬度为44°~45°带面积变形变化率达到最大值。
6) 高斯投影变换中,当Hm为负值且不小于-160 km时,其投影变形均不会超出2.5 cm/km的限差;当Hm为正值的情况下,距离中央子午线越近时,投影变形越小。
| [1] |
孔祥元. 大地测量学基础[M]. 武汉: 武汉大学出版社, 2010.
|
| [2] |
纪志刚, 余锐, 宣伟, 等. 基于CGCS2000椭球的坐标转换程序实现与精度分析[J]. 地理空间信息, 2013, 11(2): 135-137. DOI:10.11709/j.issn.1672-4623.2013.02.044 |
| [3] |
程鹏飞, 文汉江, 成英燕, 等. 2000国家大地坐标系椭球参数与GRS 80和WGS 84的比较[J]. 测绘学报, 2009, 38(3): 189-194. DOI:10.3321/j.issn:1001-1595.2009.03.001 |
| [4] |
冷继全. 高斯投影计算程序设计与实现[J]. 科技创新导报, 2018, 15(16): 81-83. |
| [5] |
唐基文, 何鹏, 李太平. 地方独立坐标系采用抵偿高程面的任意带高斯投影的分析[J]. 测绘与空间地理信息, 2012, 35(8): 186-189. DOI:10.3969/j.issn.1672-5867.2012.08.061 |
| [6] |
朱兆涵, 周晓慧. 陆态网络坐标时间序列中共模误差剔除与赫尔默特坐标变换的关系[J]. 测绘地理信息, 2017, 42(6): 36-40. |
| [7] |
何薇, 王广兴, 刘晖. 基于最佳抵偿法建立任意带坐标系的研究[J]. 测绘信息与工程, 2009, 34(6): 1-2. |
| [8] |
许超铃, 姚宜婉, 熊思婷, 等. 三维任意旋转角度坐标转损的整体最小二乘回归解法[J]. 测绘信息与工程, 2010, 35(5): 46-48. |
| [9] |
李程春, 姚宜斌, 黄承猛, 等. 探讨中国区域的WGS-84与PZ-90坐标转换参数[J]. 测绘信息与工程, 2011, 36(5): 35-37. |
| [10] |
姚宜斌, 黄书华, 张良, 等. 求解三维坐标转换参数的整体最小二乘新方法[J]. 武汉大学学报·信息科学版, 2015, 40(7): 853-857. |
| [11] |
Akyilmaz O. Total Least Squares Solution of Coor-dinate Transformation[J]. Survey Review, 2007(1): 68-80. |
| [12] |
Shen Yunzhong, Chen Yi, Zheng D H. A Quaterni-on-based Geodetic Datum Transformation Algorithm[J]. J Geod, 2006, 80: 233-239. DOI:10.1007/s00190-006-0054-8 |
| [13] |
Altamimi Z, Sillard P, Boucher C. ITRF2000:A New Release of the International Terrestrial Reference Frame for Earth Science Applications[J]. Journal of Geophysical Research, 2002, 107(B10): 2214-2232. |
| [14] |
廖中平, 沈云中, 李博峰. 顾及协方差阵的三维基准非线性变换[J]. 同济大学学报: 自然科学版, 2008, 36(9): 1286-1289. DOI:10.3321/j.issn:0253-374X.2008.09.027 |
 2021, Vol. 46
2021, Vol. 46

