| 顾及空间跨越关系的复杂道路交叉口图形简化表达 |
随着城市化进程的快速发展,简单、平面交叉路口逐渐被种类繁多、结构复杂的立交桥、匝道取代,该类要素的地图表达与制图综合难度越来越大。道路交通网络的结构识别与地图综合一直是地理信息系统(geographic information system, GIS)领域研究的重要问题[1],在地图导航、道路规划等方面发挥着重要的作用。如何针对复杂要素建立专门的地图综合方法,既能正确表达三维空间复杂的跨越关系、分支路段通达拓扑结构、交通流量各分支差异性,又能获得图形简化的表达效果,成为GIS领域研究的问题。
对道路网的综合,许多学者进行了不同方式的研究与实验[2-4],大部分都是将交叉口看作由道路网的二维平面图的节点构成,采用与道路网一般路段相同的简化方法,从基于道路等级的简单选取,到结合线状要素的图形化简[5],再到基于图论方法的道路选取[6, 7],最后考虑道路连通性、车流量的道路网综合模型[8]等,上述方法在处理没有复杂交叉口的道路时是适用的,而对于复杂道路交叉口进行综合时往往难以保持原始交叉口的跨越关系,甚至破坏道路的连通性,并且难以处理交叉口的冲突关系。
本文针对道路交叉口结构复杂、形态多样但又具有一定几何形态的特点,对交叉口的几何结构进行深入分析,建立了复杂交叉口图形库,为交叉口的结构识别提供图形模板,并对图形库中的典型交叉口提出简化的可视化策略。
1 交叉口图形模板库构建在道路网规划中,交叉口的设置、形状、规模等都有具体的规定。根据相交道路的主线标高是否相等,交叉口分为平面交叉口和立体交叉口。平面交叉口是指道路在一个平面上相交形成的交叉口,包括T型、十字型、环形等。立体交叉的道路则不处于同一平面,有高度上的跨越关系。立体交叉有分离式和互通式两种,分离式主要包括道路上的立交桥,上下方道路互不连通,互通式立体交叉设有匝道来连接上下相交道路,车辆可通过匝道跨越上下道路。
1) 平面交叉口。根据交叉处的支路数量,可将平面交叉口分为三叉型、四叉型和五叉型交叉口。还可根据交叉口形状和是否有交通岛,将平面交叉口分为三叉型、三叉渠化、三叉环、四叉型、四叉渠化、四叉环和五叉环型交叉口。具体矢量化结构如图 1所示。
 |
| 图 1 平面交叉口图形库 Figure 1 Plane Insection Graphics Library |
2) 立体交叉口。在实际道路中,立体交叉口占有很大比例,且形式丰富多样。立体交叉口分为分离式和互通式交叉,互通式立体交叉根据不同形态又可分为Y型立体交叉、喇叭型交叉、部分苜蓿叶型交叉、苜蓿叶型交叉、蝶式交叉、环形交叉和菱形交叉。具体矢量化结构如图 2所示。
 |
| 图 2 立体交叉口图形库 Figure 2 Three-Dimensional Insection Graphics Library |
由上述分类可以看出,简单交叉口(三叉型、四叉型等)不需要进行简化,而结构复杂、形态多样具有典型规律的交叉口则需要进行简化。在城市道路中,由多种结构组合而成的复杂结构交叉口较多,不但给地图导航带来困难,而且是交通拥堵、交通事故的高发地段,因此,复杂类型的交叉口是本文可视化的重点。
2 交叉口简化方法根据地图图形综合化简的基本方法,本文提出交叉口路段综合化简的两步法,一是选取道路与图形化简,二是冲突处理,建立与该操作配套的相应综合规则。整个图形简化过程为:①根据交叉口图形形态对道路进行选取,保留重要的、舍去次要的道路;②对于典型交叉口进行有针对性的化简;③当多条道路位置发生冲突时,建立相应的冲突处理原则。
1) 交叉口简化算子。地图综合算子有很多种不同的分类方法,有12个地图综合算子:简化、光滑、聚合、混合、合并、收编、精选、典型化、夸大、增强、移位和分类。其中可用于线状目标尺度变化的地图综合算子包括选取、合并、移位、光滑和典型化表达。
选取:在比例尺变化时,因为地图幅面有限,不是所有的要素都能保留下来。因此,需要保留等级高的(或者具有重要连通作用的)线要素,舍去次要的线要素。
光滑:通过重新定位或者坐标移位平滑掉小的弯曲,仅捕获最有意义的趋势线,进行了光滑处理后的线要素能够减少采样时产生的尖锐拐角。
合并:在尺度变化较大的情况下,可能无法保留单个线要素的特征,因此,这些具有相同特征的线要素需要进行合并。
典型化:当重要的要素太多或者太小而不能按比例显示的情况下,通过典型化来表达图形群落的图案特征。
移位:移位算子用于解决两个或多个要素相互冲突的问题,通过对要素进行坐标移位,或者通过符号变化或中断来修改线要素。
2) 典型结构简化表达。交叉口简化的两个重点问题是如何表达出交叉口处不同道路之间的等级关系和跨越层次关系。
通常两条道路的交叉关系有平交和立交两种,在地图上,道路通常用一个有宽度的多边形带表示,由背景描边和前景填充组成,如图 3所示,图 3中椭圆为立交关系,方形框位置为平交关系。两条道路为立交关系时,空间上高的道路背景边线和填充全部压盖高度低的道路;平交时,背景描边不压盖,等级高的道路其填充色压盖等级低的道路。
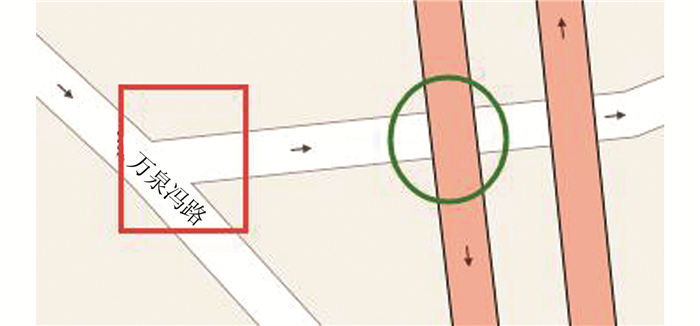 |
| 图 3 道路交叉关系 Figure 3 Road Cross Relationship |
本文以苜蓿叶型立体交叉口为例,讨论简化方法和可视化规则,如图 4所示。苜蓿叶型立体交叉口是最古老也是应用最广泛的一种形式,通过匝道实现两车道4方向的行驶。根据该交叉口处道路的等级,使用道路综合中的选取算子,选择等级高的两条主路,舍去等级低的匝道。先根据不同比例尺与图幅要求,对不同等级道路采用不同颜色和宽度的线状符号,用箭头表现出该道路上的车辆通行方向。
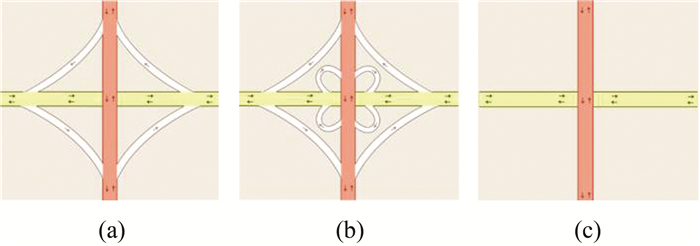 |
| 图 4 苜蓿叶型交叉口图形化简 Figure 4 Graphic Simplification of Alfalfa Leaf Intersection |
3) 冲突处理。现实生活中的交叉口通常为不同类型交叉口在不同层次上的混合,因此不同层级交叉口在同一平面上表现时的冲突处理是重点。针对同一个地理位置的交叉口,对比常用的开放街道数据(OpenStreetMap,OSM)、百度地图和腾讯地图,如图 5所示,发现同一空间不同高度道路在冲突处理时没有统一的标准[9]。
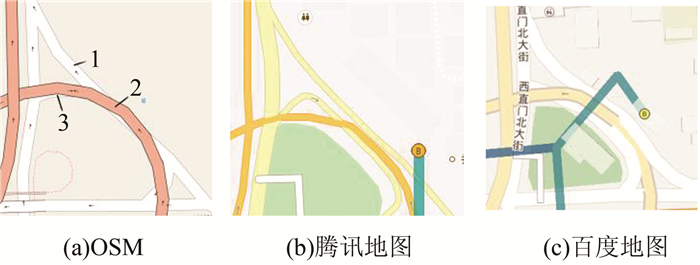 |
| 图 5 OSM、腾讯地图和百度地图在西直门桥处交叉口图 Figure 5 Xizhimen Bridge Intersection of OSM, Tencent Map and Baidu Map |
在冲突处理的过程中,所使用到的地图综合算子包括光滑、移位和合并算子。综合过程中,要尽量减少地理变形和移位,保持道路间的相对关系。对比图 5(a)、图 5(b)和图 5(c)可以看到,编号为1、2、3的3条道路在同一平面表现时存在压盖关系。根据制图学中的常见规则,冲突处理时,保持等级高的道路位置不变,对等级低的要素进行移位处理,同时保持相对关系不变。该示例中,道路1和2均为主干道,综合考虑道路等级和道路长度因素,编号为2的道路位置保持不变,将1进行移位,保证道路1和道路2不压盖,舍去为支路的道路3,同时,合并在地理空间上没有间隔的两条道路,可以减少地图上的交叉点。进行冲突处理后的交叉口如图 6所示。
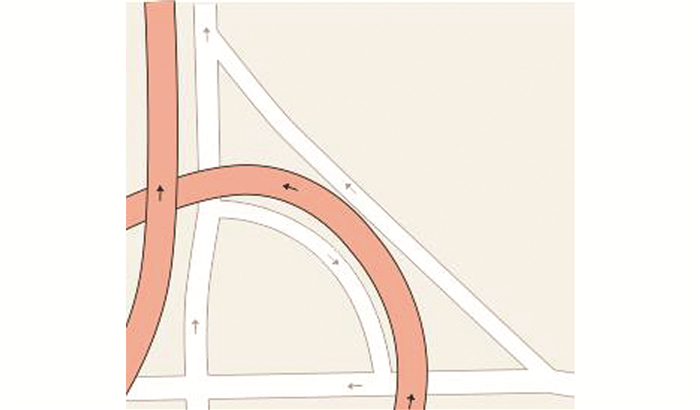 |
| 图 6 冲突处理后的西直门桥交叉口 Figure 6 Xizhimen Bridge Intersection After Conflict Handling |
3 道路交叉口化简处理实验 3.1 数据提取与组织
OSM文件描述采用的是包含拓扑性质的数据结构,用节点、道路和关系等要素来描述GIS中的点、线、面等几何信息。OSM中一条街道包含node、way和relation三个元素,node表示一段道路的端点,way表示路径,relation表示道路之间的关系,所有这些要素都有标签tag,以描述具体的属性信息。
在OSM中, 道路数据主要存储于way要素中,并通过标签tag中的highway键来标识, 而道路的等级分类则通过highway键的值来反映, 包括了motorway、motorway_Link、trunk、trunk_Link、primary、primary_Link、secondary、tertiary、residental、service、track、Pedestrian、junction、aroundabout等。
由于后缀名为.osm的文件是基于XML格式进行存储的,为了对道路要素直接进行操作,本文选择从第三方网站Trimble Data Marketplace下载选定的Shapefile数据直接在ArcGIS中进行处理。
3.2 交叉口可视化实验基于ArcGIS和CorelDRAW,对北京市多处交叉口进行设计和绘制,从而构建相关图形模板化简的规则,并用实验数据进行验证。
如图 7所示,实验区域一为OSM中北京西直门处的交叉口,在对该交叉口进行简化时,根据它的空间高度划分成两层独立的交叉口,对道路进行分级。对于上层立交桥,先把南北朝向和东西朝向的西直门桥主干道各自合并为一条道路进行显示,再根据道路的等级和长度,保留长的、重要的道路,舍去短的、次要的道路;下层立交桥是一个比较典型的苜蓿叶形交叉口,可直接将小段匝道删除。
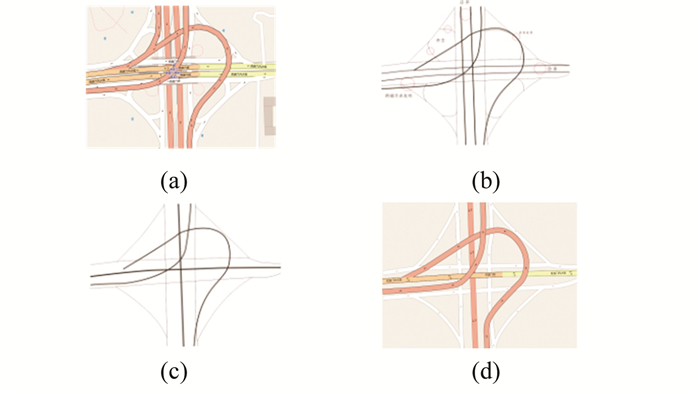 |
| 图 7 实验区域一 Figure 7 Experimental Area One |
空间上呈现跨越关系的两层交叉口在平面上会产生部分重叠,在这种情况下,保持上层立交桥的主要道路位置不变,对下层立交桥交叉的路段进行移位操作。
如图 8所示,在对实验区域二进行简化时,上层交叉口路段比较复杂,可以拆分为多个分离式立体交叉和Y形交叉口,再分别进行简化。这样简化的优点是在地图比例尺缩小时,由于有限的幅面无法承载过多的信息,因此对信息进行取舍,只呈现出最重要的信息,用户在使用地图时不至于被混乱的幅面和冗余信息干扰。这样简化的缺点就是无法表现出全部的地图信息,道路之间的拓扑关系也会产生变化,需要再进行调整。
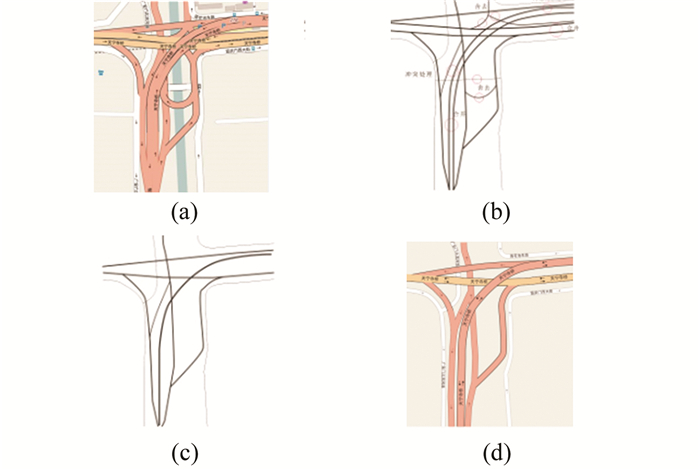 |
| 图 8 实验区域二 Figure 8 Experimental Area Two |
4 结束语
本文总结了道路网中常见的交叉口几何形态特征,并对其进行分类,构建典型交叉口图形模板库,对已有的图形库进行丰富和扩充。针对复杂交叉口的空间跨越关系,提出了道路交叉口化简与可视化表达的基本方法,并构建了综合化简规则。由上述实例应用结果可以看出,本方法能够有效地解决交叉口在平面表达上的空间跨越关系和冲突处理。
本方法挖掘出了交叉口形态学上的深层次规律,丰富了立交桥图形库,同时还可以对后期的自动识别提供支持。本文仅对道路交叉口图形识别算法和可视化规则进行了初步设计,今后需要进一步建立综合化简的图形规则,并设计相应的自动综合操作算法,实现复杂道路交叉口的自动化简。
| [1] | 姜晓睿, 田亚, 蒋莉, 等. 城市道路交通数据可视分析综述[J]. 中国图象图形学报, 2015, 20(4): 454–467 DOI: 10.11834/jig.20150401 |
| [2] | 应申, 李霖. 制图综合的知识表示[J]. 测绘信息与工程, 2003, 28(6): 26–28 |
| [3] | Heinzle F, Anders K H, Sester M. Graph Based Approaches for Recognition of Patterns and Implicit Information in Road Networks[C]. Proceedings of the 22nd International Cartographic Conference, A Coruna, Spain, 2005 |
| [4] | Touya G. A Road Network Selection Process Based on Data Enrichment and Structure Detection[J]. Transactions in GIS, 2010, 14(5): 595–614 DOI: 10.1111/tgis.2010.14.issue-5 |
| [5] | 邹广黔, 李静, 吴孔江. 基于多比例尺地图数据的线状要素综合方法[J]. 测绘地理信息, 2014, 39(4): 62–64 |
| [6] | Jiang B, Claramunt C. A Structural Approach to the Model Generalization of an Urban Street Network[J]. GeoInformatica, 2004, 8(2): 157–171 DOI: 10.1023/B:GEIN.0000017746.44824.70 |
| [7] | Jiang B, Harrie L. Selection of Streets from a Network Using Self-Organizing Maps[J]. Transactions in GIS, 2010, 8(3): 335–350 |
| [8] | Mustière S. Cartographic Generalization of Roads in a Local and Adaptive Approach: A Knowledge Acquistion Problem[J]. International Journal of Geographical Information Science, 2005, 19(8/9): 937–955 |
| [9] | 张英辉, 张水平, 张凤琴, 等. 基于OpenStreetMap最短路径算法的分析与实现[J]. 计算机技术与发展, 2013, 23(11): 37–41 |
 2018, Vol. 43
2018, Vol. 43

