| 相关观测的L1范数最小化方法的比较分析 |
2. 中国科学院大地测量与地球动力学国家重点实验室,湖北 武汉,430077
2. State Key Laboratory of Geodesy and Earth's Dynamics of Chinese Academy of Sciences, Wuhan 430077, China
为了保证测量成果达到精度要求,在完成实测任务后,必须进行测量数据的质量分析[1]。粗差会对最小二乘(least-square, LS)估计造成不良影响,对观测值进行质量分析,削弱粗差对观测值的不良影响,显得十分必要。粗差处理方法一直是测量数据处理领域关注和讨论的热点[2-4]。
粗差处理的方式主要有粗差探测和抗差估计[4-5]两种。L1范数最小化方法是其中一种抗差估计方法,就计算效率而言,基于最小化残差平方和的L2范数最小化方法比基于最小化绝对值残差的L1范数最小化方法具有明显的优势,但在抗差性方面,两者恰好相反。为了降低粗差对未知参数估值的不良影响,L1范数最小化方法无疑是一种更好的选择,其在测量领域得到了深入研究和广泛应用[6-9]。
采用线性规划方法即采用权阵的对角线元素构造目标函数,忽略了观测之间的相关性,这种相关性是否对其产生重大影响,有待进一步讨论。如果通过Cholesky分解,将相关观测转化为独立等权观测,则容易造成粗差转移[10-11]。除了应用线性规划理论求解L1范数最小化问题,另外一种重要方法是采用选权迭代,该方法的适用性同样值得思考。鉴于此,本文就观测之间相关性对L1范数最小化方法进行了Monte Carlo比较分析。
1 G-M模型的L1范数最小化方法G-M模型[6]为:
| $ \mathit{\boldsymbol{b}} = \mathit{\boldsymbol{AX}} + \mathit{\boldsymbol{ \boldsymbol{\varDelta} }} $ | (1) |
式中,b是n×1观测向量;A是n×t系数矩阵;X是t×1未知参数向量;Δ为随机误差向量,随机模型表示为:
| $ E(\mathit{\boldsymbol{ \boldsymbol{\varDelta} }}) = \mathit{\boldsymbol{AX}}, D(\mathit{\boldsymbol{ \boldsymbol{\varDelta} }}) = \sigma _0^2{\mathit{\boldsymbol{P}}^{ - 1}} $ | (2) |
式中,σ02为单位权方差;P为n×n权阵;E和D分别为求数学期望和协方差函数。
由残差加权平方和(Ω1)最小化原理,构造目标函数:
| $\min {\mathit{\Omega }_1} = {\mathit{\boldsymbol{V}}^{\rm{T}}}\mathit{\boldsymbol{PV}} $ | (3) |
| $ \hat X = {\left( {{\mathit{\boldsymbol{A}}^{\rm{T}}}\mathit{\boldsymbol{PA}}} \right)^{ - 1}}{\mathit{\boldsymbol{A}}^{\rm{T}}}\mathit{\boldsymbol{Pb}} $ | (4) |
对应的残差为:
| $ \mathit{\boldsymbol{V}} = \mathit{\boldsymbol{b}} - \mathit{\boldsymbol{A}}\mathit{\boldsymbol{\widehat X}} $ | (5) |
当观测值含有粗差时,基于式(3)的LS估计会严重偏离参考值,即LS估计对粗差很敏感,易受粗差的不良影响,稳健性较差。由于残差加权平方和会扩大粗差的影响,有学者提出了L1范数最小化方法,当权阵P =In时,其目标函数为[12-14]:
| $ {\mathit{\Omega }_2} = \sum\limits_{i = 1}^n {\left| {{V_i}} \right|} $ | (6) |
式中,Vi为第i个观测值的残差;Ω2为对应残差绝对值之和。L1范数最小化方法能够降低粗差对未知参数估值的不良影响。由于式(6)含绝对值,故无法通过对未知参数求偏导来获得未知参数估值。通过引入松弛变量η和ξ, α和β代替未知参数和残差:
| $ \left\{ {\begin{array}{*{20}{l}} {\mathit{\boldsymbol{V}} = \mathit{\boldsymbol{\alpha }} - \mathit{\boldsymbol{\beta }}, }&{\mathit{\boldsymbol{\alpha }}, \mathit{\boldsymbol{\beta }} \ge 0}\\ {\mathit{\boldsymbol{X}} = \mathit{\boldsymbol{\eta }} - \xi, }&{\mathit{\boldsymbol{\eta }}, \mathit{\boldsymbol{\xi }}\ge0} \end{array}} \right. $ | (7) |
将式(6)的求解转化为考虑如下最优化问题:
| $ \min {\mathit{\Omega }_2} = \left[{\begin{array}{*{20}{c}} {{{\bf{0}}^{\rm{T}}}}&{{{\bf{0}}^{\rm{T}}}}&{{\mathit{\boldsymbol{h}}^{\rm{T}}}}&{{\mathit{\boldsymbol{h}}^{\rm{T}}}} \end{array}} \right]\left[{\begin{array}{*{20}{l}} \mathit{\boldsymbol{\eta }}\\ \mathit{\boldsymbol{\xi }}\\ \mathit{\boldsymbol{\alpha }}\\ \mathit{\boldsymbol{\beta }} \end{array}} \right] $ | (8) |
约束条件:
| $ \left[{\begin{array}{*{20}{c}} \mathit{\boldsymbol{A}}&{-\mathit{\boldsymbol{A}}}&{{\mathit{\boldsymbol{T}}_n}}&{-{\mathit{\boldsymbol{T}}_n}} \end{array}} \right]\left[{\begin{array}{*{20}{c}} \mathit{\boldsymbol{\eta }}\\ \mathit{\boldsymbol{\xi }}\\ \mathit{\boldsymbol{\alpha }}\\ \mathit{\boldsymbol{\beta }} \end{array}} \right] = \mathit{\boldsymbol{b}} $ | (9) |
式中,Tn为单位权阵;hT=[1, 1, …, 1];η, ξ,α, β ≥0。
考虑观测值之间的相关性时,上述L1范数最小化方法的目标函数为[7-10]:
| $ \min {\mathit{\Omega }_3} = {\mathit{\boldsymbol{f}}^{\rm{T}}}|\mathit{\boldsymbol{V}}| $ | (10) |
式中,Ω3为加权残差绝对值之和。结合松弛变量,式(10)的求解转换为考虑如下最优化问题:
| $ \min :{\mathit{\Omega }_3} = \left[{\begin{array}{*{20}{c}} {{{\bf{0}}^{\rm{T}}}}&{{{\bf{0}}^{\rm{T}}}}&{{\mathit{\boldsymbol{f}}^{\rm{T}}}}&{{\mathit{\boldsymbol{f}}^{\rm{T}}}} \end{array}} \right]\left[{\begin{array}{*{20}{l}} \mathit{\boldsymbol{\eta }}\\ \mathit{\boldsymbol{\xi }}\\ \mathit{\boldsymbol{\alpha }}\\ \mathit{\boldsymbol{\beta }} \end{array}} \right] $ | (11) |
约束条件等同于式(9),其中f=diag(P)。目标函数式(11)没有顾及观测值之间的相关性,这种相关性是否对最终解造成影响,有待进一步分析。在相关观测抗差估计领域,将其转化为独立等权观测,容易造成粗差转移。然而,基于式(11)的目标函数是否会对L1范数最小化方法的抗差功效以及粗差探测性能造成影响,需要深入研究。
对权阵作Cholesky分解P =WTW,然后对模型式(1)两边同时乘以(WT)-1,则式(1)转化为:
| $\mathit{\boldsymbol{\bar b}} = \mathit{\boldsymbol{\bar AX}} + \mathit{\boldsymbol{ \boldsymbol{\bar \varDelta} }} $ | (12) |
式中,
| $ \min {\mathit{\Omega }_3} = \sum\limits_{i = 1}^n {\left| {{{\bar V}_i}} \right|} $ | (13) |
式中,Vi为式(12)得到的第i个残差,结合松弛变量,可以得到与式(8)和式(9)相类似的最优化问题。
1.2 基于选权迭代目标函数式(10),将其变形为:
| $ \min {\mathit{\Omega }_4} = \sum\limits_{i = 1}^n {{f_i}} \frac{{{{\left| {{V_i}} \right|}^2}}}{{\left| {{V_i}} \right|}} $ | (14) |
fi基于上述目标函数,结合抗差M估计的选权迭代思想,将1/|Vi|当作降权因子,有迭代计算式为:
| $ {\mathit{\boldsymbol{\widehat X}}^{(k + 1)}} = {\left( {{\mathit{\boldsymbol{A}}^{\rm{T}}}{{\mathit{\boldsymbol{\overline P}} }^{(k + 1)}}\mathit{\boldsymbol{A}}} \right)^{ - 1}}{\mathit{\boldsymbol{A}}^{\rm{T}}}{\mathit{\boldsymbol{\overline P}} ^{(k + 1)}}\mathit{\boldsymbol{b}} $ | (15) |
式中,
| $ \begin{array}{l} {\mathit{\boldsymbol{\overline P}} ^{(k + 1)}} = {\mathop{\rm diag}\nolimits} \left( {\sqrt {\omega _1^{(k)}} \;\;\;\sqrt {\omega _2^{(k)}} \;\;\;\; \cdots \;\;\;\;\sqrt {\omega _n^{(k)}} } \right){\mathit{\boldsymbol{\overline P}} ^{(k)}} \times \\ \;\;\;\;\;\;\;\;\;\;\;{\mathop{\rm diag}\nolimits} \left( {\sqrt {\omega _1^{(k)}} \;\;\;\;\sqrt {\omega _2^{(k)}} \;\;\;\; \cdots \;\;\;\;\sqrt {\omega _n^{(k)}} } \right) \end{array} $ | (16) |
式中,ωi(i=1, 2, …, n)为降权因子,可通过式(17)进行确定:
| ${\omega _i} = \frac{1}{{\left| {{V_i}} \right| + \varepsilon }} $ | (17) |
为了防止|Vi|=0,在其中加入一个很小的数ε。基于式(14)的目标函数,同理运用选权迭代的思想,有目标函数为:
| $ \min {\mathit{\Omega }_5} = \sum\limits_{i = 1}^n {\frac{{{{\left| {{{\bar V}_i}} \right|}^2}}}{{\left| {{{\bar V}_i}} \right|}}} $ | (18) |
式中,Ω5为对应的残差绝对值之和,可类似于式(15),得到最终的参数估值。
2 L1范数最小方法的比较分析 2.1 算例1采用文献[15]的CORS网数据,将原始数据的LS估计结果当作参考值,然后模拟出Gauss-Markov模型的观测数据,模拟步骤可查阅文献[16, 17]。为了与LS方法进行比较,在相应的观测值中随机加入6个大小为[-100, -3]和[3, 100]倍单位权中误差的粗差,然后分别采用以下5种方案进行计算。
方案1:无误差的LS估计;
方案2:含粗差的LS估计;
方案3:基于式(10)的L1范数最小化方法;
方案4:基于式(14)的L1范数最小化方法;
方案5:基于式(16)的L1范数最小化方法;
方案6:基于式(18)的L1范数最小化方法;
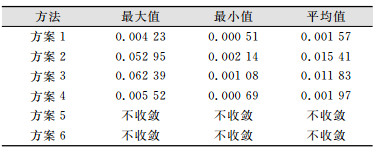
为了消除随机偶然因素的影响,随机模拟运行了200次。各方案得到的参数估值与参考值的距离的统计结果如表 1所示。从表 1可以得知,无粗差时,LS估计得到参数估值与参考值非常接近,这充分说明当观测值中不含粗差时,LS估计是一种很好的参数估计方法,无需采用其他方法就能保证成果的可靠性。当观测值中含粗差时,LS估计得到估值远远偏离参考值,这说明LS估计对粗差十分敏感,不具有抗差性。基于方案3和方案4的L1范数最小化方法能够有效抵御粗差的不良影响。方案3没有考虑观测值之间的相关性,结果相对较差,这一结果充分说明相关性对L1范数最小化方法具有重要影响。方案5和方案6收敛性较差,因而不适于求解L1范数最小化问题。
| 表 1 200次模拟各种方案的统计结果 Tab.1 Statistical Results for Each Scheme with 200 Times |
 |
2.2 算例2
为了比较方案3和方案4在粗差探测方面的功效,以文献[18]GPS向量网为例进行分析。
将大小为0.5、-0.6、-0.2、0.3和-0.4 m的粗差分别加入到第5、15、21、31和第37号观测值,得到新的观测值。为了将结果进行对比,将无粗差时的LS估计当作参考值。由方案2~方案4得到的坐标估值及其与参考值之间的欧氏距离
为了比较两种L1范数最小化方法的粗差探测效果,给出了两种方案的残差序列图,分别如图 1和图 2所示,残差序列表示对应残差的位置。
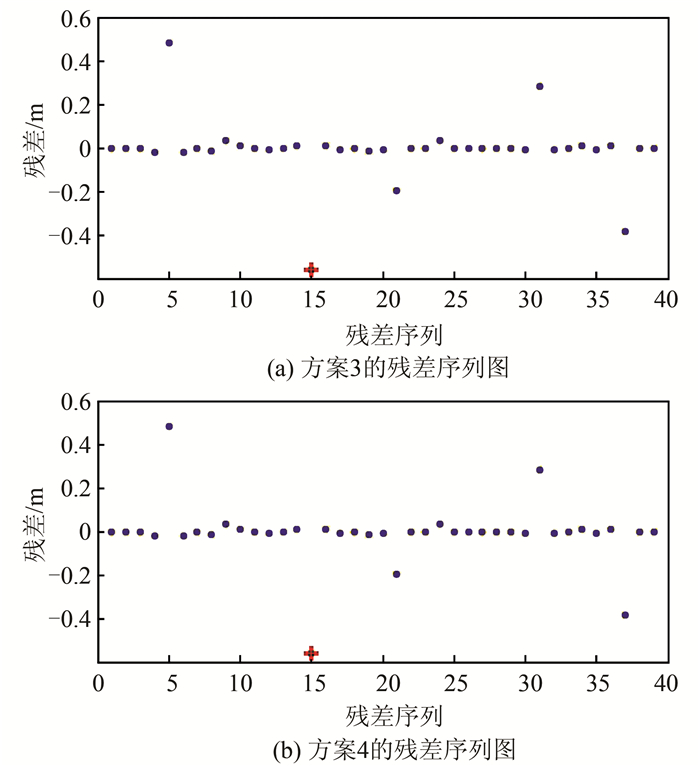 |
| 图 1 方案3和方案4的残差序列图 Fig.1 Chart of Residuals for Scheme 3 and Scheme 4 |
 |
| 图 2 剔除第15个观测值后方案3和方案4的残差序列图 Fig.2 Chart of Residuals for Scheme 3 and Scheme 4 After Deleting Observation 15 |
方案3和方案4均判断第15个观测值为粗差,于是剔除第15个观测值,可得到新的残差序列,如图 2所示。从图 2可知,方案3认为第5个观测值图中+为粗差,而方案4认为原观测值第37个观测值为粗差。继续剔除对应粗差,得到相应的残差序列。从图 3的残差序列可以判断,方案3认为原观测值序列第37个观测值为粗差,而方案4认为原观测值第31个观测值为粗差。同样,分别剔除相应的观测值,进而得到方案3和方案4新的残差序列,如图 4所示。方案3认为原观测值序列第31个观测值为粗差,而方案4认为原观测值第5个观测值为粗差。同样,分别剔除相应的观测值,得到两种方案新的残差序列,如图 5所示。
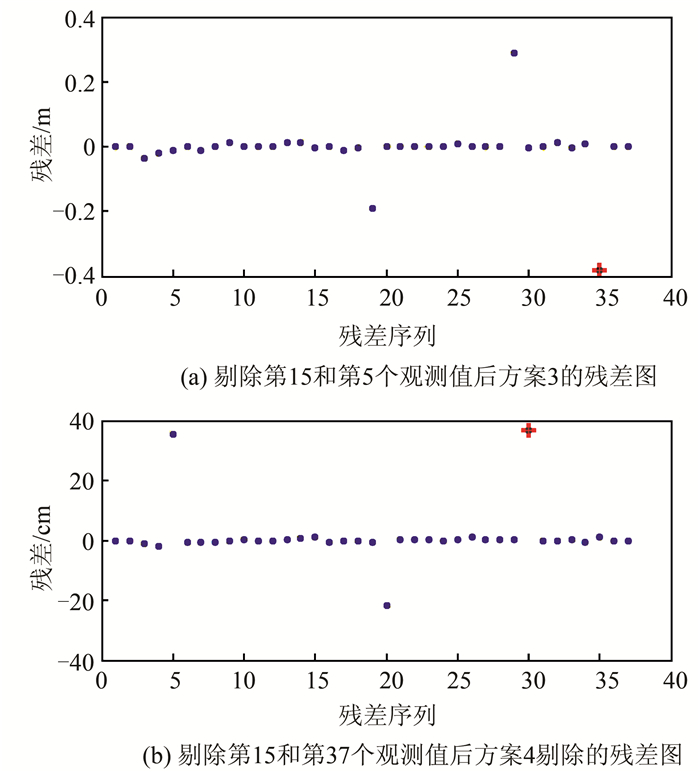 |
| 图 3 方案3和方案4剔除相应观测值后得到的残差图 Fig.3 Chart of Residuals for Scheme 3 After Deleting Observation 15 and 5 and for Scheme 4 After Deleting Observations 15 and 37 |
 |
| 图 4 方案3和方案4剔除观测值后得到的残差序列图 Fig.4 Chart of Residuals for Scheme 3 and Scheme 4 After Deleting Observation |
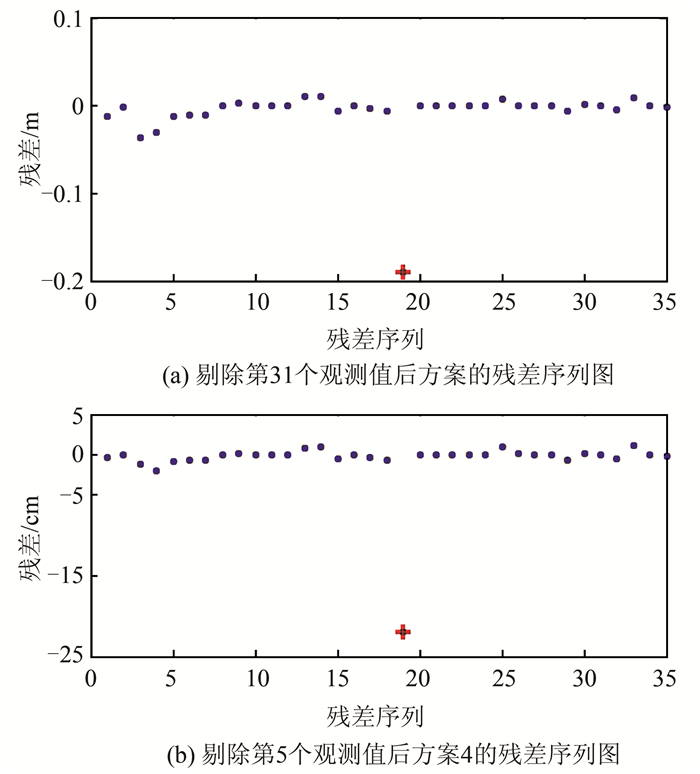 |
| 图 5 方案3和方案4剔除相应观测值后得到的残差图 Fig.5 Chart of Residuals for Scheme 3 and Scheme 4 After Deleting Observations |
图 5可知,根据模拟的粗差,方案3和方案4均有效的探测出所有粗差。在删除所有粗差后,两种方案的残差序列如图 6所示。图 6中的残差序列表明方案3和方案4中的残差序列均很小,故所有的模拟粗差均被准确识别和探测。虽然方案3和方案4探测粗差的顺序有所不同,但粗差探测结论相同。当然粗差大小是否对两种方案有影响,有待进一步研究。
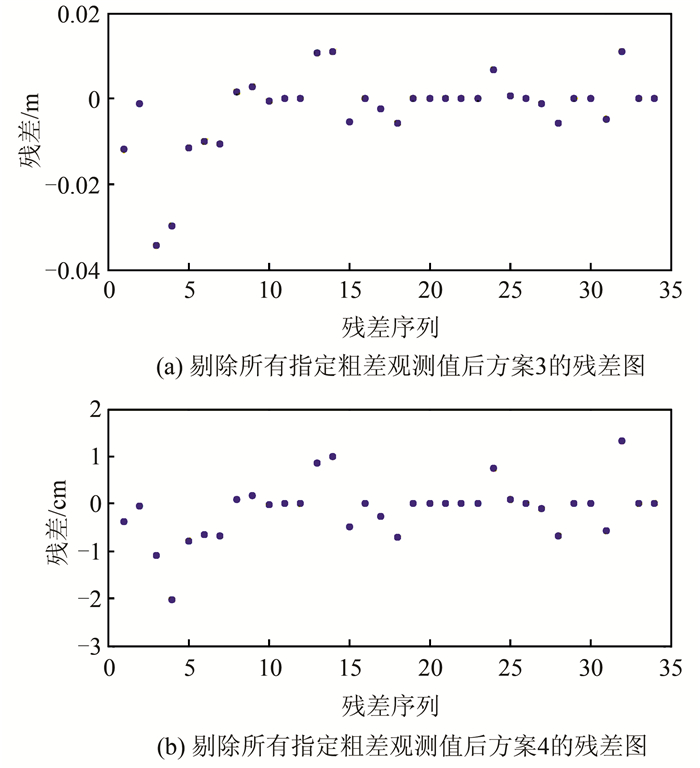 |
| 图 6 剔除所有指定粗差观测值后方案3和4得到的残差图 Fig.6 Chart of Residuals for Scheme 3 and 4 After Deleting All Pointed Outlying Observation |
3 结束语
本文针对相关观测,对L1范数最小化方法处理的不同策略进行了分析,并通过数值模拟比较了各种方法的有效性和可靠性。Monte Carlo模拟结果表明,考虑观测值相关性,没有影响其粗差识别功效,反而使得基于线性规划的L1范数方法更具稳健性,而基于选权迭代的L1范数方法收敛性较差,因而不适用于解算L1范数最小化问题。
| [1] |
郭建锋, 赵俊. 粗差探测与识别统计检验量的比较分析[J]. 测绘学报, 2012, 41(1): 14-18. |
| [2] |
Hekimlglu S, Erdogan B, Soycan M, et al. A Univariate Approach for Detecting Outliers in Geodetic Networks[J]. Journal of Surveying Engineering, 2014, 140(2): 1-8. |
| [3] |
Baselga S. Noneistence of Rigorous Tests for Multiple Outlier Detection in Least-Squares Adjustment[J]. Journal of Surveying Engineering, 2011, 137(3): 109-112. DOI:10.1061/(ASCE)SU.1943-5428.0000048 |
| [4] |
Keein I, Matsuoka M T, Guaztto M P, et al. On Evaluation of Different Methods for Quality Control of Correlated Observations[J]. Survey Review, 2015, 47(340): 28-35. DOI:10.1179/1752270614Y.0000000089 |
| [5] |
黄维彬. 近代平差理论及其应用[M]. 北京: 解放军出版社, 1992.
|
| [6] |
Koch K R. Parameter Estimation and Hypothesis Testing in Linear Models[M]. 2nd ed. Berlin: Springer Verlag, 1999.
|
| [7] |
Marshall J, Bethel J. Basic Concepts of L1 Norm Minimization for Surveying Applications[J]. Journal of Surveying Engineering, 1996, 122(4): 168-179. DOI:10.1061/(ASCE)0733-9453(1996)122:4(168) |
| [8] |
Amirir-Simkooei A. Formulation of L1 Norm Minimization in Gauss-Markov Models[J]. Journal of Surveying Engineering, 2003, 129(1): 37-43. DOI:10.1061/(ASCE)0733-9453(2003)129:1(37) |
| [9] |
Yetkin M, Inal C. L1 Norm Minimization in GPS Networks[J]. Survey Review, 2011, 43(323): 523-532. DOI:10.1179/003962611X13117748892038 |
| [10] |
Khodabadeh A, Amiri-Simkooei A R. Recursive Algorithm for L1 Norm Estimation in Linear Models[J]. Journal of Surveying Engineering, 2011, 137(1): 1-8. DOI:10.1061/(ASCE)SU.1943-5428.0000031 |
| [11] |
Xu P L. On Robust Estimation with Correlated Observations[J]. Bull Geod, 1989, 63(3): 237-252. DOI:10.1007/BF02520474 |
| [12] |
Xu P.L. Sign-constrained Robust Least Squares, Subjective Break-down Point and the Effect of Weights of Observations On Robustness[J]. Journal of Geodesy, 2005, 79(1): 146-159. |
| [13] |
郭建锋.模型误差理论若干问题研究及其在GPS数据处理中的应用[D].武汉: 中国科学院测量与地球物理研究所, 2007 http://www.wanfangdata.com.cn/details/detail.do?_type=degree&id=Y1622218
|
| [14] |
Farebrother R W. L1-Norm and L-Norm Estimation: An Introduction to the Least Absolute Residuals, the Minimax Absolute Residual and Related Fitting Procedures[M]. New York: Springer, 2013.
|
| [15] |
Snow K. Applications of Parameter Estimation and Hypothesis Testing to GPS Network Adjustments[D]. Columbur: Ohio State University, 2002 http://www.mendeley.com/research/applications-af-parameter-estimation-hypothesis-testing-gps-network-adjustments/
|
| [16] |
Yang Y, Song L, Xu T. Robust Estimator for Correlated Observations based on Bifactor Equivalent Weightes[J]. Journal of Geodesy, 2002, 76(6): 353-358. |
| [17] |
Guo J F, Ou J K, Wang H T. Robust Estimation for Correlated Observations: Two Local Sensitivity-based Downweighting Strategies[J]. Journal of Geodesy, 2010, 84(4): 243-250. DOI:10.1007/s00190-009-0361-y |
| [18] |
Ghilani C. Adjustment Computations Spatial Data Analysis[M]. 5th ed. New Jersey: John Wiley & Sons, 2010.
|
 2019, Vol. 44
2019, Vol. 44

