| 最小化最大边权的正射影像镶嵌线自动搜索 | [PDF全文] |
2. 信阳师范学院地理科学学院,河南 信阳, 464000
2. School of Geographic Sciences, Xinyang Normal University, Xinyang 464000, China
数字正射影像图(digital orthophoto map,DOM)的生产需要将多张具有重叠区域的数字微分纠正影像进行镶嵌操作,镶嵌线(亦称拼接线或接缝线)的搜索是其中一个关键的步骤[1]。镶嵌线应尽量使镶嵌影像在镶嵌线两侧无几何错位且色彩过度自然,即应尽量避免穿过建筑、树木等高出地面的地物和色彩反差大的区域[2]。在实际生产中,特别是对于城区高分辨率航摄影像,使用现有商业软件自动搜索的镶嵌线往往不能满足生产要求,还需进行较多人工编辑,生产效率较低。因此,研究镶嵌线的自动搜索方法对于提高DOM产品的质量与生产效率具有重要意义[3]。
基于重叠区影像差异的方法是最常用的镶嵌线自动搜索方法之一,其主要思想是对重叠区域中的每个像元计算差异值,得到一个差异影像,然后采用一定的搜索策略在该差异影像上选择一条两侧影像差异最小的路径作为镶嵌线[4]。文献[5]提出利用Dijkstra算法在差值影像上搜索镶嵌线,但其搜索到的镶嵌线可能是像素数量较少但像素差值较大的路线,且算法复杂度较高。文献[6]在文献[5]的基础上提出了基于最小化最大算法的镶嵌线搜索策略,有效抑制了镶嵌线在差值影像上的局部最大值。文献[7]提出利用Twin Snakes模型自动搜索镶嵌线,定义了包含色彩和纹理信息的差异测度,并通过最小化两条动态轮廓间的能量值搜索最佳路径,但该算法仅对林区影像效果好。文献[8, 9]提出基于蚁群算法的镶嵌线搜索算法,有效避开了建筑、树木等高出地面的地物及水面等反差较大的地物,但该算法效果受限于蚂蚁的数目,且效率较低。文献[10]利用影像亮度差异和梯度差异构建重叠区域差异影像,并采用最优生成树方法搜索镶嵌线,该方法回避了迭代搜索过程,效率较高。纵观以上镶嵌线搜索方法,虽然各有优点,但依然存在一定的问题,大体可归为两个方面:一方面,以上方法的差异描述基于单个像素或局部纹理,而非地物区域,因此,不能很好地反映重叠区域的几何差异,难以避免镶嵌线穿越建筑等障碍区域,为此,文献[11-13]分别提出利用数字表面模型、激光雷达和道路矢量数据等作为辅助数据搜索镶嵌线,通过辅助数据区分障碍区域和非障碍区域,使得镶嵌线避开建筑等地物,然而此类辅助数据的获取十分困难;另一方面,就搜索策略而言,现有算法大都难以在得到全局最优的镶嵌线的同时兼顾运算效率。
综合以上分析,本文提出一种最小化最大边权的镶嵌线自动搜索算法。首先,计算影像重叠区域的视差图,并将视差图和差值影像叠加得到差异影像;然后,基于Bottleneck模型将镶嵌线搜索问题转换为带权无向图中最小化最大边权路径求取问题,在差异影像上搜索最佳镶嵌线;最后,通过实验证明本文算法不仅能有效避开建筑等几何差异较大的区域,也能避开色度差异较大的区域,得到比较理想的镶嵌线。
1 基于最小化最大边权的镶嵌线搜索原理 1.1 重叠区域差异影像的生成使镶嵌线避开建筑、树木等高出地面或色彩差异大的区域的关键在于使用某种测度准确地表达影像重叠区域的差异。重叠区域的差异主要包括几何差异和色度差异。通常采用差值影像来表示两幅待镶嵌影像的色度差异,设差值影像上像素(i, j)的灰度为Δgij,其表达式为:
| $ \Delta {g_{ij}} = \left| {{g_{ij}} - {{g'}_{ij}}} \right| $ | (1) |
式中,gij、g′ ij分别为左右影像上像素(i, j)的灰度值。
几何差异主要是由摄影角度的差异造成的,DOM一般是根据数字高程模型微分纠正得到的,高出地面的地物在纠正后依然存在投影差,在多张单片正射影像上会出现在不同的位置,当镶嵌线穿越这些地物时两侧会出现几何错位。图 1(a)和图 1(b)是两幅相邻的单片正射影像;图 1(c)为相应的差值影像。可以看出,左右影像重叠区域的几何差异反映在差值影像上表现为不连续的地物轮廓线,缺乏区域连续性和完整性,不能正确反映建筑物的顶部区域,容易导致镶嵌线穿越这些区域。因此,本文使用视差图来表达左右影像重叠区域的几何差异。
 |
| 图 1 示例影像 Fig.1 Sample Image |
假设左右相机具有相同的姿态和焦距f,摄影基线长度为Tx,物点P(X, Y, Z)在左右影像上的成像几何示意图如图 2所示,d为点P在左右影像上的水平像点坐标之差,即左右视差,其表达式为:
 |
| 图 2 左右影像成像几何透视图 Fig.2 Geometric Perspective of Stereo Image |
| $ d = \left| {{x_l} - {x_r}} \right| = f\frac{{{T_x}}}{Z} $ | (2) |
式中,xl、xr分别表示该点在左右影像上的x坐标。由式(2)可知,当摄影基线和焦距一定时,像点的左右视差d与物距Z成反比,即离相机越近的物体视差越大。因此,建筑物等地物的高程越高,在左右影像上形成的视差越大,即在视差图上表现为高亮度区域,如图 1(d)所示。视差图能够准确描述出高出地面的物体的连续性区域信息,可以弥补差值影像在差异描述时的不足。
因此,本文采用差值影像与视差图相结合的差异影像来描述重叠区域的差异。首先,根据计算机视觉中的立体影像匹配原理,使用半全局约束立体匹配(semi-global matching, SGM)算法[14]计算视差图,并对其进行高斯模糊处理以确保镶嵌线远离高出地面物体的边缘;然后,根据式(1)计算重叠区域的差值影像;最后,将视差图与差值影像叠加得到最终的差异影像,如图 1(e)所示。由于视差图反映了区域级的几何差异,差值影像反映了像素级的色度差异,因此两者叠加得到的差异影像能很好地描述重叠区域的真实差异。此时,镶嵌线搜索就是在差异影像上寻找一条避开高亮度区域的最优路线,本文提出的镶嵌线自动搜索算法的总体流程如图 3所示。
 |
| 图 3 本文算法流程 Fig.3 Flow Chart of Proposed Approach |
1.2 基于最小化最大边权算法的搜索策略
本文将差异影像视为带权无向图,以BottleNeck模型[15]为基础,将镶嵌线自动搜索问题转换为带权无向图中最小化最大边权路径的求解问题。
1) 图搜索空间的构建主要包括基于差异影像的带权无向图的构建和图中边权值的设立两个问题。如图 4所示,本文将差异影像中的像素点视为无向图中的顶点,采用四邻域方法确定邻接点,即每个顶点最多存在4个邻接点(如图 4中顶点p4的邻接点为p1、p3、p5、p7),对于图像上的任一像素,其邻域可由行列号确定,因此,无需使用邻接表或邻接矩阵来表示无向图,可节省大量存储空间。若pu、pv为基于差异影像的带权无向图中的两个邻接点,其构成的边(u, v)的权值w(u, v)为pu、pv的像素值的平均值为:
 |
| 图 4 四邻域带权无向图 Fig.4 4-Neighborhood Weighted Undirected Graph |
| $ w\left( {u, v} \right) = \left( {{d_u} + {d_v}} \right)/2 $ | (3) |
式中,du、dv分别表示顶点pu、pv的像素值。
2) 最小化最大边权算法。若镶嵌线两侧影像差异最大部分的目视差异不明显,则镶嵌线两侧其他部分的目视差异更不明显,此时的镶嵌线可被视为符合要求。以上即为Bottleneck模型的基本思想,其数学模型为:
| $ \left\{ \begin{array}{l} f\left( {{P_S}} \right) = \max \left( {d\left( {i, j} \right)} \right), \left( {i, j} \right) \in {P_S}\\ \min f\left( {{P_S}} \right) \end{array} \right. $ | (4) |
式中,PS表示镶嵌线;d(i, j)表示重叠区域第i行j列的像素对应的差异值;f(PS)表示镶嵌线上差异最大值;minf(PS)表示使f(PS)最小。
左右影像重叠区域的差异值可由差异影像上的像素值来表示,此时,搜索最优镶嵌线就是要使得镶嵌线上差异影像的像素最大值最小,因此,求解Bottleneck模型实质上就是求解带权无向图的最小化最大边权路径问题。针对该问题,本文基于Dijkstra最短路径算法思想提出最小化最大边权算法,具体做法是对于一个带权无向图,给定起点S和终点E,引入两个集合W和U,W存放已搜索过的顶点,U存放待计算的顶点,初始时两个集合均为空,f表示顶点到起点S的路径上的最大边权值,w(u, v)表示邻接点u和v的边权值。
算法具体步骤如下:①将起始点S放入集合U中,且f(S)取值为0,此时,集合W为空。②从集合U中查找f值最小的顶点k,将k加入集合W中,如果k就是终点E,路径查找结束。③如果k不是终点E,则找到k的所有邻接点k′ i(i=1, 2, 3, 4)。此时,k′ i的最大边权值f(k′ i)= max(p(k, k′ i), f(k))。若k′ i不在集合W中,则将k′ i加入集合U,转步骤②;若k′ i已在集合W中且f(k′ i)比原值小,则更新W中f(k′ i)的值,转步骤②。
本文算法与Dijkstra算法的最大区别在于对每个顶点计算的不是该点到起点的路径长度,而是该点到起点的路径上的最大边权。因此,可以避免搜索到的镶嵌线是总像素数较少而差异值较大的路径,能够得到更优的镶嵌线。
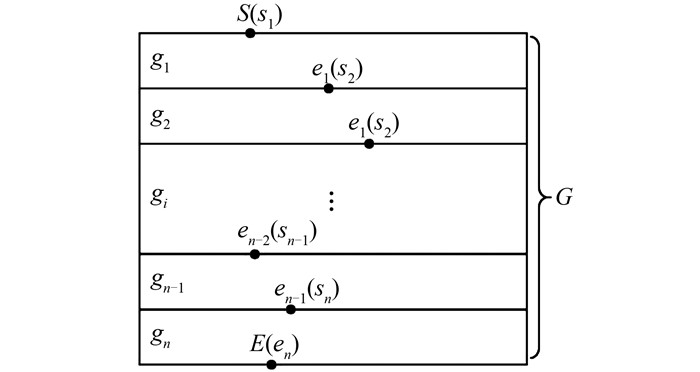
3) 算法性能优化。根据影像重叠区域的差异影像逐像素建立带权无向图进行最小化最大边权路径搜索所需的计算量较大,因此,本文采用分块策略对其进行优化,如图 5所示。首先,将带权无向图G按行等距分割为多个子图gi;然后,从上至下依次计算每个子图的最小化最大边权路径,对于除图G终点E所在子图外的每个子图gi,当集合W中的新增点位于该子图的最后一行时停止搜索,并将该点视为该子图的终点ei和下一子图的起点si+1,而图G的终点则为图G终点所在的子图的终点;最后,将所有子图的最小化最大边权路径相连即可得到图G的最小化最大边权路径。优化前的最小化最大边权算法的时间复杂度为O(n×log(n)),而优化后的时间复杂度可降为O(n×log(n/m)),其中,n表示图中顶点的数目,m表示子图个数。
 |
| 图 5 算法效率优化 Fig.5 Efficiency Optimization of the Algorithm |
2 实验结果分析
1) 实验设计。为验证本文算法的可行性,使用Visual C++编程实现了本文提出的正射影像镶嵌线自动搜索算法,并在配备Intel Pentium双核E5400、2.6 GHz CPU和4 GB内存的台式计算机上进行实验。首先,在密集建筑区和稀疏建筑区两种类型的影像上进行有效性实验;然后,将本文算法的正射影像镶嵌效果与现有的逐行检测算法、Dijkstra算法和最优生成树算法做出对比分析。
2) 镶嵌线质量分析。实验影像的地物类型主要包括房屋、道路、树木和湖泊等,影像大小为1 200像素×1 666像素,空间分辨率为0.1 m,图 6(a)为密集建筑区影像,图 6(b)为稀疏建筑区影像,图 6(c)、图 6(d)分别为其对应的差异影像,搜索到的镶嵌线均用白线显示在影像上。
 |
| 图 6 镶嵌线搜索结果 Fig.6 Results of Seamline Detection |
从图 6中可以看出,本文所使用的差异影像不仅可以有针对性地突出显示高出地面的地物目标,还能显示重叠区域色度差异细节。从整体上来看,镶嵌线很好地避开了地面建筑物和较高的树木,无论在密集建筑区还是稀疏建筑区,镶嵌后的影像上均基本没有镶嵌痕迹。
在差异影像上,理想的镶嵌线应沿着灰度值小的区域前进,参考基于差分影像的镶嵌线搜索方法,给出定量评价镶嵌线质量的两个指标:①差异影像上镶嵌线的像素最大灰度值最小;②差异影像上镶嵌线的像素平均灰度值最小,其表达式如下:
| $ \left\{ \begin{array}{l} {C_1} = \min \left( {\max \left( {{d_{ij}}} \right)} \right), \left( {i, j \in {P_S}} \right)\\ {C_2} = \min \left( {\frac{{\sum {{d_{ij}}} }}{{L\left( {{P_S}} \right)}}} \right), \left( {i, j \in {P_S}} \right) \end{array} \right. $ | (5) |
式中,dij表示差异影像上第i行j列像素的灰度值;L(PS)表示镶嵌线PS上的像素个数。
表 1统计了两个实验区的实验数据,可以看出,本文算法在密集建筑区表现良好,如式(5)所示的像素最大灰度指标和像素平均灰度指标均优于稀疏建筑区,这是由于稀疏建筑区的微分纠正影像在纠正时存在一定误差,导致地面也存在较大投影差,生成的视差图质量不高,因此,镶嵌线不可避免地穿越了差异影像上亮度较高的区域,但镶嵌线在镶嵌后的正射影像上并没有穿越建筑和树木等高出地面的区域,镶嵌效果依然比较理想,这表明本文算法具有较好的鲁棒性。
| 表 1 镶嵌线质量与效率统计 Tab.1 Quality and Efficiency of the Seamlines |
 |
3) 与现有算法对比分析。为了与其他算法比较,采用逐行检测算法、Dijkstra算法、最优生成树算法和本文算法分别对相同影像区域进行镶嵌线搜索实验。实验影像包括密集建筑区和稀疏建筑区的影像,空间分辨率为0.1 m,大小分别为600像素×2 179像素和400像素×1 276像素,实验结果如图 7所示。
 |
| 图 7 种算法效果对比图 Fig.7 Comparison of 4 Kinds of the Algorithms |
表 2为逐行检测算法、Dijkstra算法、最优生成树算法和本文算法在密集建筑区和稀疏建筑区上的镶嵌线质量和效率统计数据。
| 表 2 密集和稀疏建筑区镶嵌线质量与效率对比 Tab.2 Contrast of Quality and Efficiency of Seamlines in Dense Building Area and Sparse Building Area |
 |
由图 7和表 2可知,从效率上看,逐行检测算法效率最优,本文算法为得到高精度的视差图耗时稍多于Dijkstra算法和最优生成树算法。从目视效果来看,逐行检测算法搜索到的镶嵌线在一定程度上沿着地物边缘前进,但仍多次穿越建筑物和树木等地物,镶嵌效果不理想,Dijkstra算法和最优生成树算法得到的镶嵌线效果有所提升,穿越建筑物和树木的次数少于逐行检测算法,而本文算法几乎没有穿越建筑物和树木,基本避开了高出地面的地物和色度差异较大的区域,镶嵌效果具有较大优势。从定量指标来看,在平均灰度、最大灰度和大灰度像素数3个方面,本文算法搜索到的镶嵌线均优于其他算法,依据式(5)所示的两个镶嵌线质量评价指标,说明本文算法得到的镶嵌线质量最为理想。
图 8为多张影像的镶嵌结果,可以看出,本文算法对于多张影像的镶嵌效果理想,镶嵌线基本避开了建筑物,沿道路或建筑边缘前行。
 |
| 图 8 多张影像镶嵌结果 Fig.8 Multiple Image Seamlines |
3 结束语
本文提出最小化最大边权的镶嵌线自动搜索算法,通过视差图和差值影像共同构建差异影像并视其为带权无向图,采用最小化最大边权算法计算无向图上的最优路径作为镶嵌线,并采取分块搜索策略提高算法效率。实验结果表明,本文算法得到的镶嵌线能有效避开影像中高出地面和色度差异较大的地物区域,从而得到高质量的镶嵌影像。从目视效果和定量指标上来看,本文算法的镶嵌线搜索结果在可容忍的时间内均优于逐行检测、Dijkstra和最优生成树等现有算法。
| [1] |
张祖勋, 张剑清. 数字摄影测量学[M]. 武汉: 武汉大学出版社, 1997.
|
| [2] |
潘俊, 王密, 李德仁. 接缝线网络的自动生成及优化方法[J]. 测绘学报, 2010, 39(3): 289-294. |
| [3] |
张静, 杨博, 王密, 等. 基于资源3号影像的全国DOM快速制作方法[J]. 测绘地理信息, 2016, 41(6): 70-74. |
| [4] |
周清华, 潘俊, 李德仁. 遥感图像镶嵌接缝线自动生成方法综述[J]. 国土资源遥感, 2013, 25(2): 1-7. |
| [5] |
Davis J. Mosaics of Scenes with Moving Objects[C].IEEE Computer Society Conference on Computer Vision and Pattern Recognition, Santa Barbara, CA, USA, 1998
|
| [6] |
Jaechoon C, Hyongsuk K, Chun S L. Seam-Line Determination for Image Mosaicking: A Technique Minimizing the Maximum Local Mismatch and the Global Cost[J]. ISPRS Journal of Photogrammetry and Remote Sensing, 2010, 65(1): 86-92. DOI:10.1016/j.isprsjprs.2009.09.001 |
| [7] |
Kerschner M. Seamline Detection in Colour Orthoimage Mosaicking by Use of Twin Snakes[J]. ISPRS Journal of Photogrammetry and Remote Sensing, 2001, 56(1): 53-64. DOI:10.1016/S0924-2716(01)00033-8 |
| [8] |
张剑清, 孙明伟, 张祖勋. 基于蚁群算法的正射影像镶嵌线自动选择[J]. 武汉大学学报·信息科学版, 2009, 34(6): 675-678. |
| [9] |
孙明伟.正射影像全自动快速制作关键技术研究[D].武汉: 武汉大学, 2009
|
| [10] |
陈继溢, 许彪, 张力, 等. 采用最优生成树的正射影像镶嵌线快速智能检测[J]. 测绘学报, 2015, 44(10): 1125-1131. DOI:10.11947/j.AGCS.2015.20140467 |
| [11] |
左志权, 张祖勋, 张剑清, 等. DSM辅助下城区大比例尺正射影像镶嵌线智能检测[J]. 测绘学报, 2011, 40(1): 84-89. |
| [12] |
孙杰, 马洪超, 汤璇. 机载LiDAR正射影像镶嵌线智能优化研究[J]. 武汉大学学报·信息科学版, 2011, 36(3): 325-328. |
| [13] |
Wan Youchuan, Wang Dongliang, Xiao Jianhua, et al. Automatic Determination of Seamlines for Aerial Image Mosaicking Based on Vector Roads Alone[J]. ISPRS Journal of Photogrammetry and Remote Sensing, 2013, 76: 1-10. DOI:10.1016/j.isprsjprs.2012.11.002 |
| [14] |
Hirschmuller H. Accurate and Efficient Stereo Processing by Semi-Global Matching and Mutual Information[C].IEEE Computer Society Conference on Computer Vision and Pattern Recognition, San Diego, USA, 2005
|
| [15] |
Fernandez E, Garfinkel R, Arbiol R. Mosaicking of Aerial Photographic Maps via Seams Defined by Bottleneck Shortest Paths[J]. Operation Research, 1998, 46(3): 293-304. |
 2020, Vol. 45
2020, Vol. 45

