| 高分六号高分辨率相机在轨几何定标方法与精度验证 |
2. 湖北工业大学计算机学院,湖北 武汉,430060
2. School of Computer Science, Hubei University of Technology, Wuhan 430060, China
随着卫星遥感技术的飞速发展,卫星影像逐渐发展成高空间、时间、光谱分辨率的星系。国际上著名的星系有SPOT[1]系列、IKONOS[2]、Pleiades[3]、IRS-P[4]系列、ALOS[5]等,中国也研发并发射了天绘一号[6]、资源三号[7]、高分专项系列卫星。
高分六号搭载了2 m/8 m的高分辨率相机(简称高分相机)及16 m的宽幅相机。高分相机首次采用了96 km的成像幅宽,将有效提高中高分辨率遥感数据的获取规模,增强时效性;同时高分相机将会为宽幅相机提供更高精度的几何基准,从而辅助其进行在轨几何处理。卫星发射入轨后,为了消除卫星在发射、运行过程中由复杂环境因素引起的误差,需要进行在轨几何定标以保证几何定位能力。
海外学者借助高精度的地面检校场对SPOT卫星进行在轨几何定标,内部畸变经标定能优于0.1像素[1]。Baltsavias等[8]采用高精度控制数据对IKONOS进行在轨几何定标,定标后影像的定位精度优于5 m,高程精度优于3 m;Lussy等[9]仅利用一定数量的控制点对Pleiades进行在轨几何定标,定标精度提升有限;Radhadevi等[10]用地面定标场对IRS-P6、KOMPSAT2等卫星实现了精确的在轨几何定标;Takaku等[11]借助密集的控制点,利用线性回归对ALOS PRISM进行绝对内部定标,定标后影像实现了子像素级的片间拼接,立体像对的平面、高程精度均优于2 m[12, 13]。
随着国内卫星定标场[14]的建设,王建荣等[15]利用东北数字定标场对天绘一号卫星进行整体标定,定标后无控平面、高程精度分别达到10.3 m、5.7 m;王密等[16]基于高分四号卫星数据分析了静止轨道卫星成像几何误差源及成像区域的特点,提出了其严格几何成像模型;并对星上的载荷进行在轨几何定标,定标后影像内部畸变能够达到子像素级。杨博[17]对卫星成像链路误差进行分析,提出了基于探元指向角模型的分步定标方法,并利用嵩山定标场对资源三号数据进行了实验验证。本文基于以上研究,结合高分六号高分相机光学配置进行在轨几何定标,基于不同地物类型、空间位置、成像角度等对定标后的结果进行检验。
1 高分六号高分相机简介高分相机为单台中心投影离轴相机,光学镜头采用离轴三反光学系统,相机焦平面采用8片多光谱集成的单向时间延时积分电荷耦合元件(time delayed and integration charge coupled device,TDICCD),通过反射镜光学拼接,不同于传统推扫线阵卫星采用视场拼接方式实现“品字形”排列的TDICCD拼接处理,能在轨实现全色波段(panchromatic band,PAN)和4个多光谱谱段TDICCD的物理“共线拼接”。高分相机焦面采用8片五色集成的TDICCD通过反射镜拼接组成。光谱成像仪各谱段位置关系见图 1。
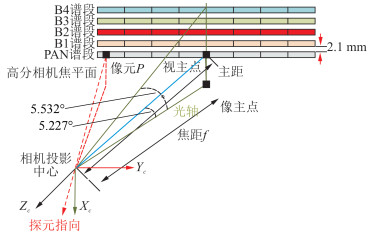 |
| 图 1 高分相机各谱段位置关系示意图 Fig.1 Diagram of Position Relationship Between Bands of High-Resolution Camera |
2 高分相机在轨几何定标模型与方法 2.1 高分相机在轨几何定标模型
在轨几何定标旨在消除严密成像模型中的各项系统误差,系统误差主要分为外部误差与内部误差。相机安装角是高分相机外部误差的主要来源,对相机安装角进行标定是外部误差标定的关键[18],相机安装角已经建立了相应的数学模型。对于相机内部,存在各项难以模型化的物理畸变,且多项误差之间存在很强的相关性,难以剥离,导致标定后的精度不稳定,因此需要在外定标参数确定的“相机坐标系”下采用探元指向角作为内定标模型,如图 2所示。
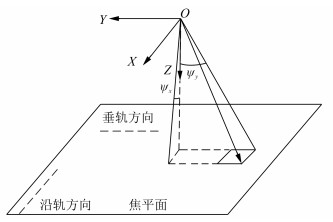 |
| 图 2 探元指向角模型示意图 Fig.2 Diagram of Detector Directional Angle Model |
为了标定TDICCD上所有探元的光束指向,线阵上不同探元的编号不同,可利用一组参数结合探元号来拟合每个探元的探元指向角,经过实验验证,采用三阶模型便可以高精度地描述探元指向角:
| $ \left\{\begin{array}{l} \psi_{x}(s)=a x_{0}+a x_{1} \times s+a x_{2} \times s^{2}+a x_{3} \times s^{3} \\ \psi_{y}(s)=a y_{0}+a y_{1} \times s+a y_{2} \times s^{2}+a y_{3} \times s^{3} \end{array}\right. $ | (1) |
式中,ax0、ax1、ax2、ax3、ay0、ay1、ay2、ay3是与探元号相关的用以确定探元指向角的内定标参数;s代表垂轨方向上的探元号。
2.2 高分相机在轨几何定标流程高分六号高分相机采用的在轨几何定标方案为基于探元指向角模型先外定标后内定标,先绝对定标后相对定标。卫星在轨的姿态轨道等参数测量精度高,但是相机在卫星本体的安装关系会出现偏移,从而产生外部系统差,因此需要先标定外部相机安装关系,标定后的外部安装关系将提供精确的广义参考,从而进行内部畸变标定,采用探元指向角模型实现内部畸变的标定。以上定标流程基于具有一定典型性的影像的PAN结合高精度数字正射影像图(digital orthophoto map,DOM)、数字高程模型(digital elevation model,DEM)进行,称为绝对定标;多光谱段的几何定标基于标定后的PAN进行,称为相对定标。高分相机在轨几何定标流程见图 3。
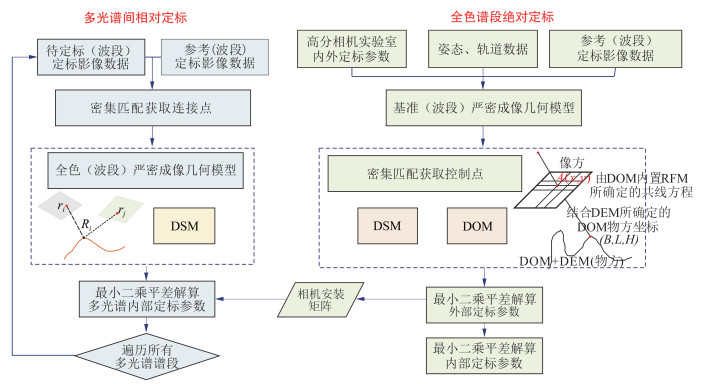 |
| 图 3 高分相机在轨几何定标流程 Fig.3 On-orbit Geometric Calibration Process of High-Resolution Camera |
2.2.1 PAN绝对定标
绝对定标时,选取具有一定特征的对地观测影像与覆盖该区域的高精度DOM、DEM进行密集匹配,获取大量在垂轨方向上铺满,沿轨方向上一段距离,整体呈矩形区域的均匀分布的虚拟控制点。本文以实验室检校的定标参数为初始值,基于最小二乘分步解算外部相机安装矩阵以及与内部探元号相关的内部检校参数,从而进行在轨几何绝对定标。
2.2.2 多光谱段间相对定标多光谱段间相对定标旨在对除PAN外的其他多光谱影像基于已经实现误差标定的PAN参数实现各片TDICCD内部畸变的标定。根据外部定标参数的物理意义,其可为内部畸变的标定提供广义的外部参考,因此绝对定标求取的外部定标参数适合作为同一视场下任一谱段、分片CCD的外部定标参数。几何定标的关键是选取合适的多光谱基准波段,以建立多光谱与PAN之间的相对关系。选取基准波段时,要同时兼顾多光谱与PAN的辐射一致性,从而可基于绝对定标后的高精度PAN实现多光谱段影像的几何定标。
高分相机搭载的多光谱段共有4个波段,每个波段由8片TDICCD构成焦面。经过实验与测试分析发现,相对于PAN以及其他多光谱段,B2谱段有较好的匹配效果,与焦面的几何关系适中。
1)B2谱段与绝对定标后的PAN通过密集匹配可以获取大量像方连接点,连接点的匹配原则同绝对定标一致,ri、rj为一对分别与PAN、B2对应的连接点。PAN可以基于绝对定标所确定的内、外参数构建严格成像模型,结合DEM可将PAN对应的像方连接点ri投影至高程面从而确定其所对应物点的空间坐标Ri。
2)将Ri作为控制点,那么其在B2谱段影像上所对应的像方点则为rj,利用最小二乘平差方法对B2谱段进行内定标参数的解算。
3)与步骤1)中B2谱段基于PAN的定标过程类似,以B2谱段为基准谱段,对B1、B3、B4谱段进行内定标参数的求解,从而完成高分相机在轨几何定标。
3 实验与分析 3.1 实验数据为了确保在轨几何定标的精度,选择的绝对定标景要有以下特点:①选取无侧摆或侧摆较小的高分相机对地观测遥感影像;②为了保证“虚拟控制点”采集的数量与精度,应该选取通视效果好、地物特征明显且地形高程差异较小的地区。除以上特征外,相对定标景选取时,地区地物类型还应具有丰富的纹理特征,往往选取戈壁沙漠地区的影像作为谱段间相对定标的定标景。本文选取的待定标影像的详细信息见表 1,选取的定标景影像及其参考影像缩略图见图 4,图 4(a)、图 4(d)中红色边框圈定了参考数据在卫星影像上的覆盖范围。本文定标参考为唐山检校场的高精度DOM与DEM,DOM的空间分辨率为0.36 m,DEM空间分辨率为5 m。
| 表 1 定标影像详细信息 Tab.1 Detail Information of Calibration Images |
 |
 |
| 图 4 卫星定标景影像数据与参考影像数据 Fig.4 Satellite Calibration Images and Reference Images |
3.2 几何定标精度分析
对所选定标景与参考数据进行绝对定标与相对定标,每片TDICCD均获取了均匀分布的控制点,通过剔除粗差较大的点来进行定标参数的求解,定标后的外部安装参数结果如表 2所示。
| 表 2 高分相机外定标参数 Tab.2 External Calibration Parameters of High-Resolution Camera |
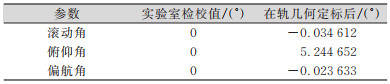 |
图 5展示了高分相机各线阵内部畸变曲线,可以看出,垂轨方向上,从星下点成像线阵到影像边缘线阵畸变值逐渐变大,沿轨方向上,从影像起始行开始到一景影像的末尾行畸变值逐渐增大。由此可见,在轨几何定标对消除垂轨、沿轨方向的畸变是十分必要的。
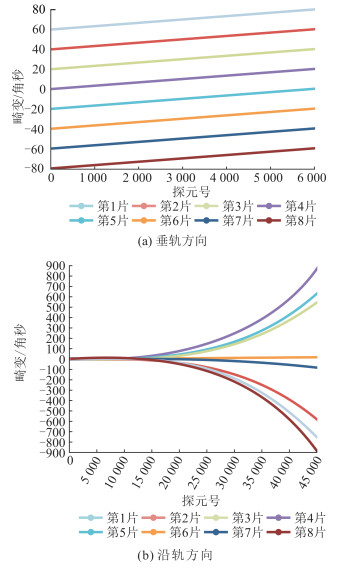 |
| 图 5 高分相机各线阵内部畸变曲线 Fig.5 Internal Geometric Distortion Curve of Each Linear Array in High-Resolution Camera |
如表 3所示,对PAN进行在轨几何绝对定标后,消除了卫星成像几何定位精度的系统差,绝对定标后各成像线阵的绝对定位精度在垂轨、沿轨方向上均优于2 m,相对定位精度在垂轨、沿轨方向上均优于1个全色像素。整景影像的绝对定位精度在垂轨、沿轨方向上均优于2.5 m,相对定位精度在垂轨、沿轨方向上均优于1个全色像素。
| 表 3 绝对定标前后的绝对定标景几何精度 Tab.3 Geometric Accuracy of Absolute Calibration Images Before and After Absolute Calibration |
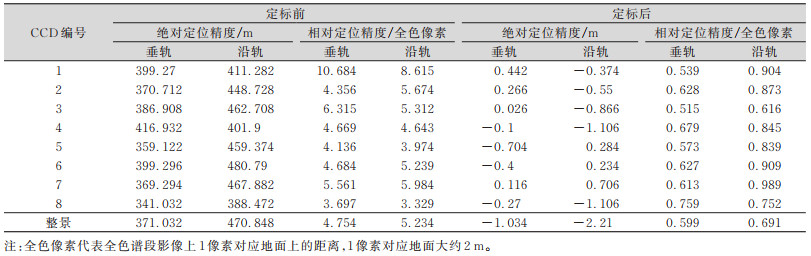 |
如表 4所示,对于定标后相对定标景的波段间配准精度主要是从整景尺度来评断,相对于PAN的波段配准精度,定标后B2谱段在垂轨、沿轨方向上均优于0.3个多光谱像素,B1、B3、B4相对B2谱段的波段配准精度在垂轨、沿轨方向也均优于0.3个多光谱像素,鉴于B2谱段在焦面上的几何关系,B1、B3、B4波段配准精度依次降低。
| 表 4 相对定标景波段配准精度 Tab.4 Band Registration Accuracy of Relative Calibration Images |
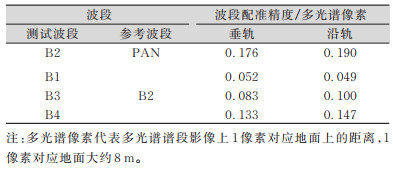 |
3.3 几何定位精度与多光谱配准精度检验
本文选取多组数据基于新定标参数生产了1A级产品,其中20景数据用来检验几何定位精度,13景数据用来检验多光谱配准精度,选取的数据具有一定典型性与随机性,选择通视效果好的影像保证了和参考影像匹配同名点的数量与质量,影像地物类型丰富。
表 5展示了测试景的几何精度。测试的参考数据为空间分辨率为2 m的DOM和5 m的DEM。根据测试结果可知,过滤样本中的奇异值后,绝对定位精度在垂轨和沿轨方向上的均值绝对值均优于15 m,在平面上的均值也近似15 m。过滤样本中的奇异值后,相对定位精度在垂轨和沿轨方向上的均值分别为1.053和1.496个全色像素。由于不同时间成像姿态、轨道的差异,不同测试景仍具有一定的系统差,经测试可得系统差优于15 m,内部精度稳定,剔除粗差后,内部畸变优于1.5个全色像素。
| 表 5 测试景几何精度 Tab.5 Geometric Accuracy of Test Images |
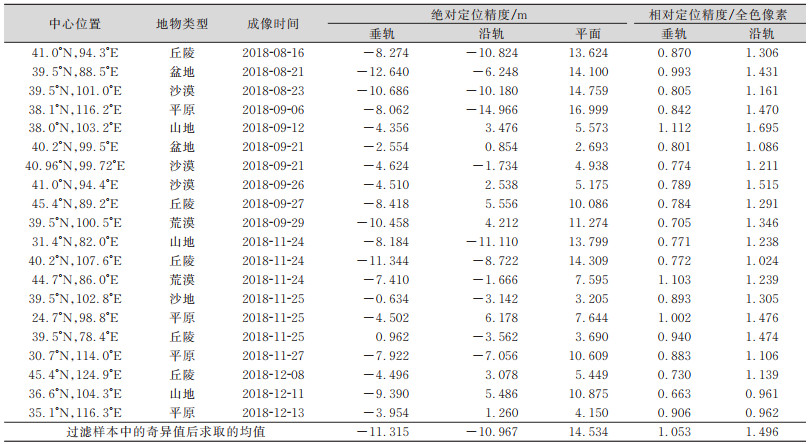 |
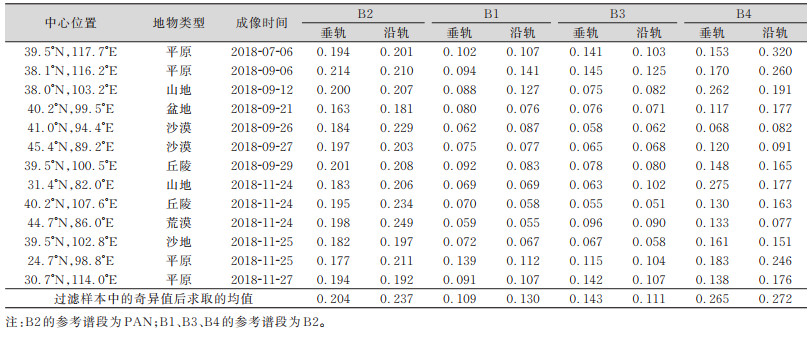
表 6展示了测试景波段配准精度,可以看出,多光谱间配准精度均优于0.3个多光谱像素,完全满足了多光谱多波段合成的容差,为后续进行影像融合等工作提供了几何条件。同时这也印证了内定标参数的稳定性优于外定标参数,且其对不同的影像产品具有一定普适性。
| 表 6 测试景波段配准精度/多光谱像素 Tab.6 Band Registration Accuracy of Test Images/multispectral pixel |
 |
4 结束语
本文采用基于相机安装矩阵、探元指向角的几何成像模型,结合高分六号高分相机的光学配置参数与几何特点,提出适用于高分六号高分相机的先外定标再内定标,先绝对定标再相对定标的在轨几何定标方法。在轨几何定标实验中采用覆盖唐山地面检校场的高精度高分辨率影像数据进行绝对定标,采用纹理特征丰富的影像进行多光谱相对定标,并利用定标后获取的定标参数生产了多个测试影像的1A级产品,评价了绝对定位精度、相对定位精度及多光谱配准精度,在无控制点的情况下,相较于相对定位精度,选取的测试景的绝对定位精度存在较大的系统差;多光谱配准精度也达到子像素级,以上均证明了内定标参数的稳定性。
| [1] |
Breton E, Bouillon A, Gachet R, et al. Pre-flight and In-flight Geometric Calibration of SPOT5 HRG and HRS Images[J]. International Archives of Photogram-metry Remote Sensing and Spatial Information Sciences, 2002, 34(1): 20-25. |
| [2] |
Bouillon A, Breton E, de Lussy F, et al. SPOT5 HRG and HRS First In-flight Geometric Quality Results[C]. SPIE Proceedings Sensors, Systems, and Next-Generation Satellites Ⅵ, Crete, Greece, 2003
|
| [3] |
Greslou D, de Lussy F, Delvit J M, et al. Pleiades-HR Innovative Techniques for Geometric Image Quality Commissioning[J]. ISPRS-International Archives of the Photogrammetry, Remote Sensing and Spatial Information Sciences, 2012, 39-B1(1): 543-547. |
| [4] |
Srivastava P K, Alurkar M S. Inflight Calibration of IRS-1C Imaging Geometry for Data Products[J]. ISPRS Journal of Photogrammetry and Remote Sensing, 1997, 52(5): 215-221. DOI:10.1016/S0924-2716(97)00014-2 |
| [5] |
Takaku J, Futamura N, Iijima T, et al. High Resolution DEM Generation from ALOS PRISM Data-Simulation and Evaluation[C]. 2004 IEEE International Geoscience and Remote Sensing Symposium, Anchorage, AK, USA, 2004
|
| [6] |
王任享. 天绘一号卫星无地面控制点摄影测量关键技术及其发展历程[J]. 测绘科学, 2013, 38(1): 5-7. |
| [7] |
李德仁. 我国第一颗民用三线阵立体测图卫星: 资源三号测绘卫星[J]. 测绘学报, 2012, 41(3): 317-322. |
| [8] |
Baltsavias E, Li Z, Eisenbeiss H. DSM Generation and Interior Orientation Determination of IKONOS Im-ages Using a Testfield in Switzerland[J]. Photogram metrie Fernerkundung Geoinformation, 2006(1): 41. |
| [9] |
de Lussy F, Greslou D, Dechoz C, et al. Pleiades HR in Flight Geometrical Calibration: Location and Mapping of the Focal Plane[J]. The International Archives of the Photogrammetry, Remote Sensing and Spatial Information Sciences, 2012, 39-B1: 519-523. |
| [10] |
Radhadevi P V, Solanki S S. In-flight Geometric Calibration of Different Cameras of IRS-P6 Using a Physical Sensor Model[J]. The Photogrammetric Record, 2008, 23(121): 69-89. DOI:10.1111/j.1477-9730.2007.00453.x |
| [11] |
Takaku J, Tadono T. PRISM On-Orbit Geometric Calibration and DSM Performance[J]. IEEE Transactions on Geoscience and Remote Sensing, 2009, 47(12): 4060-4073. DOI:10.1109/TGRS.2009.2021649 |
| [12] |
Gruen A, Kocaman S, Wolff K. Calibration and Validation of Early ALOS/PRISM Images[J]. The Journal of the Japan Society of Photogrammetry and Remote Sensing, 2007, 46(1): 24-38. |
| [13] |
Radhadevi P V, Müller R, d'Angelo P, et al. In-flight Geometric Calibration and Orientation of ALOS/ PRISM Imagery with a Generic Sensor Model[J]. Photogrammetric Engineering & Remote Sensing, 2011, 77(5): 531-538. |
| [14] |
张永生. 高分辨率遥感测绘嵩山实验场的设计与实现: 兼论航空航天遥感定位精度与可靠性的基地化验证方法[J]. 测绘科学技术学报, 2012, 29(2): 79-82. DOI:10.3969/j.issn.1673-6338.2012.02.001 |
| [15] |
王建荣, 王任享. "天绘一号"卫星无地面控制点EFP多功能光束法平差[J]. 遥感学报, 2012, 16(S1): 112-115. DOI:10.11834/jrs.20120023 |
| [16] |
王密, 程宇峰, 常学立, 等. 高分四号静止轨道卫星高精度在轨几何定标[J]. 测绘学报, 2017, 46(1): 53-61. |
| [17] |
杨博. 光学线阵推扫式卫星影像在轨几何定标理论与方法研究[D]. 武汉: 武汉大学, 2014
|
| [18] |
Wang M, Yang B, Hu F, et al. On-Orbit Geometric Calibration Model and Its Applications for High-Resolution Optical Satellite Imagery[J]. Remote Sensing, 2014, 6(5): 4391-4408. DOI:10.3390/rs6054391 |
 2022, Vol. 47
2022, Vol. 47


