| 基于多因子加权的遥感制图最佳波段组合分析 |
2. 武汉市测绘研究院,湖北 武汉,430022
2. Wuhan Geomatics Institute, Wuhan 430022, China
多光谱遥感影像因其波段信息丰富的特点被广泛应用于土地利用与覆盖监测、专题信息提取、地图编绘与更新等研究中[1, 2],而多光谱波段组合是遥感影像制图的关键技术之一[3, 4]。Landsat系列卫星自其发射以来持续提供高质量的地表多光谱影像,是重要的遥感研究信息源,其波段组合研究主要包括基于影像波段信息的指标计算和基于土地覆盖分类的精度评价两个方面。
一方面,基于影像波段信息的指标计算方法在最佳波段组合分析中广泛应用。例如,Dwivedi等[5]调查了Landsat TM影像20种波段组合的最佳指数因子指标,提出B1-B3-B5组合最适宜提取盐渍化土壤。李秀梅等[6]基于Landsat TM/ETM+影像进行了光谱统计分析,确定了B7-B4-B2波段组合方案以更好地提取海岸线的变化信息。王莉等[7]基于Landsat TM影像,综合了相关系数和最佳指数因子指标,选择B7-B4-B1组合作为兖州市土地利用覆盖变化表达的最佳波段组合。郭力娜等[8]基于Landsat-8 OLI影像,根据最佳指数因子及不同土地利用类型的光谱特征曲线确定B1-B5-B7为土地利用特征提取的最佳波段组合。
另一方面,将土地覆盖分类精度作为评价波段组合最为重要的因素。例如,Yu等[9]基于Landsat-8OLI影像和SVM分类器,确定了B4-B5-B6、B1-B2-B5-B7波段组合用于研究区土地覆盖分类的精度最高。类似地,Elhag[10]基于Landsat-8 OLI影像和最大似然分类器,确定了B4-B5-B6、B4-B5-B6-B7、B3-B4-B5-B6-B7为适宜典型地中海森林分类的最佳波段组合。
在以上两类最佳波段组合分析研究中,基于指标计算的方法采用不同的评价指标可能得到不同的结论,且少有兼顾信息提取与制图效果的最佳波段组合研究;基于分类精度评价的方法所获得的结论高度依赖于研究区域且过程繁琐、计算量大,难以推广到大区域的遥感影像最佳波段选取研究。鉴于此,本文在已有研究的基础上,基于长江经济带区域的Landsat-8 OLI影像数据,提出了多因子加权的最佳波段组合分析方法,从全局加权与场景加权的角度研究最佳波段组合方案,在提高信息提取精度的同时确保遥感影像目视效果,为长江经济带区域等大区域的遥感制图的波段组合选取提供参考。
1 研究区与数据长江经济带是我国规模最大、经济发展水平最高的经济带,横跨中国东、中、西三大区域,地处97°21′E~123°10′E, 21°8′N~34°19′N,总面积达205万km2,覆盖了全国陆地总面积的21%,人口和生产总值均占全国1/4以上。其以长江为依托,以洞庭湖、鄱阳湖等湖泊为生态环境支撑点,集中了水、城市、湿地、草场、生物等要素,有着重要的经济地位、生态地位及较强的发展潜力。
实验数据选用了成像时间为2017年5月至2017年8月、空间分辨率为30 m的118景Landsat-8多光谱影像,如图 1(a)所示。参考Yu等[9]的研究,本文剔除了空间分辨率较粗且缺乏对比度的热红外波段以方便影像处理,只保留红、绿、蓝(Red、Green、Blue)可见光波段,近红外波段(NIR)、短波红外波段(SWIR1、SWIR2)及海岸波段(Coastal)。原始L1T级影像数据已经过系统辐射校正和几何校正处理,后经大气校正、云去除、影像裁剪及匀色镶嵌预处理后[11],获得了空间无缝、色彩均衡的长江经济带区域卫星影像图,如图 1(b)所示。
 |
| 图 1 研究数据 Fig.1 Research Data |
2 研究方法 2.1 多因子指标计算
描述影像波段信息量及波段间相关性的指标包括标准差、信息熵、相关系数、最佳指数因子等,依据参与指标计算的影像波段数量,将评价指标划分为单波段、双波段及多波段评价指标,以单波段与双波段指标作为辅助参考,遵循3个主要原则:①单个波段信息量尽可能大;②波段信息冗余量尽可能小;③研究地物类型的光谱差异尽可能大,以便于地物特征的提取与分析[11]。对多波段指标进行归一化加权处理以便于确定最佳波段组合。
2.1.1 单波段指标标准差与方差:标准差与方差是概率统计学中常用的度量样本数据离散程度的指标,可用于反映各波段像元灰度值DN(digital number)总体的离散程度,各波段图像的标准差越大,表明其包含的信息越丰富,地物的边界越明显,目标越容易区分与提取[12]。
信息熵:信息熵指信息中排除冗余后的平均信息量[13],可用于描述各波段影像中所包含的平均信息量,波段影像中各灰度级出现的概率即为此灰度级像元信号所发出的信息。
2.1.2 双波段指标皮尔逊相关系数:相关系数是度量两变量间线性相关程度的指标,可用于描述两波段信息重叠程度。
协方差:协方差是衡量两个变量总体误差的指标,将波段影像看作具有正态分布的随机变量,两波段间的相关性可由协方差度量。
方差膨胀系数(variance inflation factor, VIF): VIF表示多元回归模型和一元回归模型的方差比值[14],可用于评价多光谱影像波段之间的多重共线性[9]。
2.1.3 多波段指标最佳指数因子(optimum index factor, OIF): OIF为Chavez[15]提出的针对波段组合的指标,可用于获取包含信息量较大且各波段信息冗余度较小的波段组合。其公式如下:
| $ \mathrm{OIF}=\sum\limits_{i=1}^3 S_i / \sum\limits_{j=1}^3\left|R_{i j}\right| $ | (1) |
式中,Si为i波段标准差;Rij为i、j波段相关系数。
协方差矩阵行列式值:协方差矩阵是多光谱遥感数据分析中最重要的数学概念之一[16],其行列式值可用于最佳波段组合评价。Sheffield等[17]提出基于N维数据熵值原理的图像熵值法,结果同协方差矩阵行列式值呈正相关。任意三波段组合协方差矩阵如下:
| $ \boldsymbol{\Sigma}_s=\left|\begin{array}{ccc} \boldsymbol{S}_1^2 & \boldsymbol{C}_{12} & \boldsymbol{C}_{13} \\ \boldsymbol{C}_{21} & \boldsymbol{S}_2^2 & \boldsymbol{C}_{23} \\ \boldsymbol{C}_{31} & \boldsymbol{C}_{32} & \boldsymbol{S}_3^2 \end{array}\right| $ | (2) |
式中,Si2为i波段方差;Cij为i、j波段的协方差。
2.2 多因子加权多因子加权阶段包括全局加权与场景加权两部分。全局加权即对长江经济带区域影像全局的指标进行加权分析。场景加权以选取的城市、水体、植被场景为样本,在最佳波段组合评价中将研究区域的典型地表覆盖比例纳入考虑。
2.2.1 全局加权根据式(1)、式(2)统计长江经济带区域的影像特征,采用较为综合的最佳指数因子与协方差矩阵行列式值进行全局的最佳波段组合分析。为消除不同因子数值差异的影响,本文采用z-score方法(见式(3))对计算结果进行标准化处理,并将两项指标分别赋予50%的权重计算其综合分数。
| $ X_{\mathrm{norm}}=\frac{X-\mu_X}{\sigma_X} $ | (3) |
式中,X为最佳指数因子值或协方差矩阵行列式值,μ为样本数据均值,σ为样本标准差。
2.2.2 场景加权本文设定了以发达城区为主体的城市场景、以河流与湖泊为主体的水体场景、以森林及非森林自然区域(耕地、草地、灌木地等)为主体的植被场景三大场景。在研究区域选取部分典型场景区域为样本(空间分布见图 1(b)),并分别计算适宜各场景信息表达的最佳波段组合方案。
1) 分场景指标计算。具有不同光谱特征的场景有不同的最佳波段组合。根据式(1)~式(3),分别对3个场景的样本数据进行指标计算与统计,可获得城市、水体、植被3个场景下适宜的最佳波段组合,可为不透水面、水体等地物信息提取与目视解译提供波段组合参考。
2) 考虑地表覆盖比例的场景加权。根据2020年度的Globe Land30土地覆盖产品[18]在长江经济带范围内的统计结果,城市、水体、植被场景所占比例约为4%、3%、93%。为使覆盖面积占比较小的城市与水体场景在定量计算中有更大的贡献,赋予城市∶水体∶植被比为2∶2∶6的权重比例,对分场景的指标计算结果进行场景加权分析。
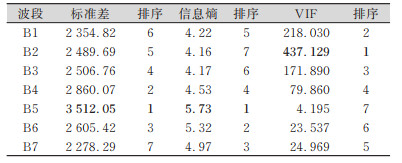
3 结果与分析 3.1 全局加权结果各波段的标准差及信息熵计算结果如表 1所示。综合两个单波段信息量指标可认为近红外波段(B5)、短波红外波段(B6)具有较高的信息量,可优先选择。
| 表 1 各波段标准差、信息熵、VIF值 Tab.1 Standard Deviation, Information Entropy, VIF of Each Band |
 |
7个波段的皮尔逊相关系数矩阵如图 2所示。可以看出,除B5波段外(R45=0.27、R56=0.26),各波段倾向于与其邻近波段有较强的相关性。以0.9为临界值,B1~B4、B6~B7波段间的相关性较强。
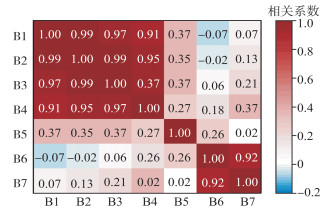 |
| 图 2 相关系数矩阵 Fig.2 Correlation Coefficient Matrix |
各波段的VIF值如表 1所示。当VIF≥10时,可认为数据多重共线性严重[19]。可以看出,除B5外的波段均有较为为严重的多重共线性,且4个较大的VIF值源于B1~B4波段,相关分析和多重共线性分析均说明波段B1~B4高度相关,尤其是B1与B2波段。此外,波段B6和B7也高度相关。因此,可在B1~B4波段、B6~B7波段中各选择1个波段,并在任意组合中包含B5波段。
根据式(1)、式(2)计算所得的OIF值与协方差矩阵行列式值,经式(3)标准化及加权的结果如图 3所示。可以看出,两个多波段指标计算结果具有很好的一致性。其中,B1-B5-B6、B1-B5-B7、B2-B5-B6、B2-B5-B7、B3-B5-B6、B3-B5-B7、B4-B5-B6、B4-B5-B7这8种波段表现出明显的优势。特别地,最佳波段组合方案B4-B5-B6同时符合单波段信息量评价与双波段相关性评价的选取策略。
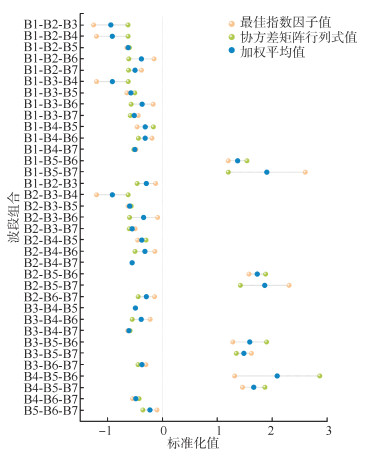 |
| 图 3 波段组合评分全局加权结果 Fig.3 Fig 3 Index Weighted Results of Overall Area |
3.2 场景加权结果 3.2.1 分场景指标计算
根据§2.2提出的多因子指标加权方法,对选取的城市、水体、植被场景下的样本进行指标计算与统计。结果表明,城市场景的最佳波段组合为B4-B5-B7,而水体与植被场景下的最佳波段组合均为B4-B5-B6。ESRI提供的常用波段组合方案[20]认为适合植被分析的波段组合包括B5-B4-B3、B5-B6-B2、B6-B5-B4,适合水体提取的波段组合为B5-B6-B4,与本文指标计算的结果较为一致。
3.2.2 考虑地表覆盖比例的场景加权在多场景指标计算结果的基础上,根据2∶2∶6计算比例赋予计算权值,统计城市、水体和植被场景的综合加权分数,选择最终得分最高的8组波段组合进行分析,如表 2所示。
| 表 2 不同波段组合多因子场景加权得分结果 Tab.2 Scene Weighted Results of Different Band Combinations |
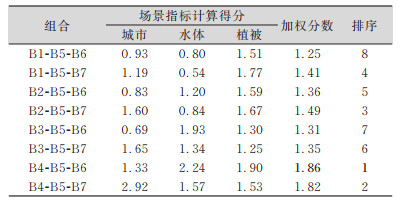 |
分析结果表明,场景加权结果与全局加权结果基本一致,排名较高的8位仍为B1/B2/B3/B4-B5-B6/B7的交叉组合,其中B4-B5-B6、B4-B5-B7组合有较大优势,B4-B5-B6组合为最适合长江经济带区域遥感制图的波段组合。在多指标加权中有较好的表现的B1-B5-B7组合排名下降(第2~4名),其主要原因是B1-B5-B7组合在植被场景下得分较高(1.77),在城市、水体场景下得分较低(1.19、0.54),而植被为长江经济带区域主要的地表覆盖类型,因此在B1-B5-B7合成影像中,城市、水体不能得到均衡的表达。B4-B5-B6的组合既满足了信息量大、信息冗余小的地物分类及提取要求,也兼顾了多场景均衡表达的制图需要。
结合人眼判读习惯和实际目视结果,本文将人眼最为敏感的绿色赋予信息量最大的波段,蓝色赋予信息量较少的波段,即因此赋予B6、B5、B4波段于红、绿、蓝三色进行假彩色合成。在此种彩色合成结果中,植被区域呈黄绿色调,湖泊水体呈深蓝色调,积雪区域呈浅蓝色,层次明显、色彩丰富、各类地物边界明显且配色符合目视判读习惯,包含较大信息量且有较好的目视效果,最终制图结果示例如图 4所示。此方案与NASA(National Aeronautics and Space Administration)的土地覆盖与土地利用变化项目中用于变化检测与制图的Landsat ARD(analysis ready data)产品[21]展示所采用的波段组合方案一致,也验证了实验结论的可靠性。
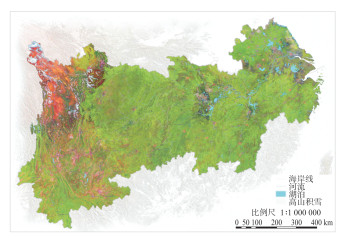 |
| 图 4 长江经济带遥感影像图 Fig.4 Remote Sensing Image of the Yangtze River Economic Zone |
3.3 结果验证
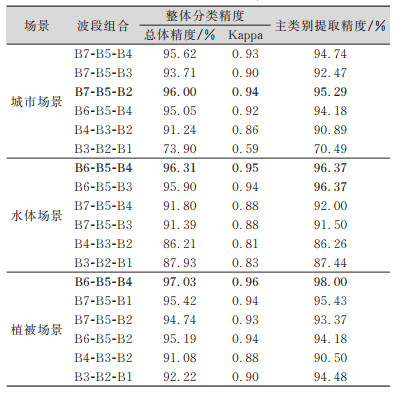
为了进一步检验最佳波段组合方案的可靠性,本文从分类精度的角度对实验结果进行验证。在城市、水体、植被3个典型场景中选取影像样本,并采用最大似然分类法进行监督分类。训练样本提取于4个土地覆盖产品Globe Land30[18]、FROM-GLC[22]、GLC_FCS30[23]、CLCD[24]分类结果完全一致且异质性较小的区域,3类场景分别选取了23 696、85 431、49 963个样本点,经人工目视检查,有较高可信度。测试样本由人工目视选取,城市、水体、植被场景各有525、232、437个样本点,整体与主要地表覆盖类别(分别为不透水面、水体、林地)的分类精度评价结果如表 3所示。结果表明,各个场景指标计算得分较高(排名1~4)的波段组合整体分类精度及主类别提取精度较高,明显高于指标计算得分较低的B4-B3-B2、B3-B2-B1波段组合。城市场景下整体分类精度最高的波段组合为B7-B5-B2,主要类别不透水面的F-Score达到95.29%。水体场景与植被场景下整体分类最高的波段组合均为B6-B5-B4,主要类别(水体与森林)分类的F-Score分别为96.37%、98%。同时,B6-B5-B4组合在城市、水体、植被场景中均保持着较高分类精度(分别为95.05%, 96.31%, 97.03%)。分类精度评价结果与指标计算的结果较为一致,验证了实验结论的可靠性。
| 表 3 分类精度评价 Tab.3 Classification Accuracy Evaluation |
 |
3.4 讨论
长江经济带区域的整体与分场景的实验结果表明,最佳指数因子和协方差矩阵行列式值在应用于同一数据集时表现出整体相似但不完全一致的结果。两个统计指标是以获得目视解译信息最大化的波段组合为目标而采取的不同的优化方法,其差异主要来源于对单波段信息量(方差或标准差)的权重设置[25]。本文通过两指标加权获得多个候选组合以支持长江经济带遥感影像制图的最佳波段组合分析。
在不同区域遥感影像的针对性研究中,相关系数与最佳指数因子[5, 7]等统计指标被广泛使用,地物光谱特征曲线[3, 6]、分类精度[9, 10]、地类OIF值排名[8]等因子也作为辅助信息被纳入最佳波段组合的分析中。本文总结了常用的最佳波段组合方法,分析相关系数与多重共线性、最佳指数因子与协方差矩阵行列式值等指标的一致性与差异来源,并将土地覆盖类型的面积比例引入典型场景的指标计算,通过多因子加权获得的最佳波段组合分析结果更为全面可信且能有效提高影像制图的目视效果。
4 结束语本文基于长江经济带区域2017年Landsat-8OLI影像数据集,建立了基于多因子加权的最佳波段组合评价方法,确定长江经济带区域遥感制图的最佳波段组合。实验结果表明,B6、B5、B4进行RGB彩色合成是兼顾了信息提取精度与制图目视效果的最佳波段组合。应当注意的是,城市区域的最佳波段组合为B5-B7-B4,水体和植被区域的最佳波段组合为B6-B5-B4。这为类似的大区域遥感影像制图的波段选择提供了一定的参考。此结果与ESRI提供的常用波段组合以及NASA的Landsat ARD产品采用的波段组合一致,验证了实验结论的可靠性。
| [1] |
武汉市近20年土地利用/覆被变化遥感监测与分析[J]. 测绘地理信息, 2021, 46(5): 83-87. |
| [2] |
基于Landsat-8卫星OLI遥感影像和AdaBoost算法的水体信息提取[J]. 测绘地理信息, 2017, 42(3): 44-47. |
| [3] |
基于Landsat 8影像的湿地信息提取最佳波段组合[J]. 地球环境学报, 2014, 5(5): 339-343. |
| [4] |
多特征组合的TM影像EnMap-Box土地利用分类[J]. 测绘地理信息, 2019, 44(3): 109-112. |
| [5] |
Dwivedi R S, Rao B R M. The selection of the Best Possible Landsat TM Band Combination for Delineating Salt-Affected Soils[J]. International Journal of Remote Sensing, 1992, 13(11): 2051-2058. DOI:10.1080/01431169208904252 |
| [6] |
渤海湾海岸带遥感监测及时空变化[J]. 国土资源遥感, 2013, 25(2): 156-163. |
| [7] |
基于多时像TM/ETM+影像的兖州市土地利用/覆盖变化[J]. 测绘科学, 2009, 34(3): 171-174. |
| [8] |
最佳波段组合的城市土地利用类型提取[J]. 测绘科学, 2019, 44(8): 161-167. |
| [9] |
Yu Zhiqi, Di Liping, Yang Ruixing, et al. Selection of Landsat 8 OLI Band Combinations for Land Use and Land Cover Classification[C]. 2019 8th International Conference on Agro-Geoinformatics(Agro-Geoinformatics), Istanbul, Turkey, 2019.
|
| [10] |
Elhag M. Consideration of Landsat-8 Spectral Band Combination in Typical Mediterranean Forest Classification in Halkidiki, Greece[J]. Open Geosciences, 2017, 9(1): 468-479. |
| [11] |
赵无双. 长江经济带遥感影像制图应用与分析[D]. 武汉: 武汉大学, 2020.
|
| [12] |
Price J C. An Approach for Analysis of Reflectance Spectra[J]. Remote Sensing of Environment, 1998, 64(3): 316-330. |
| [13] |
Shannon C E. A Mathematical Theory of Communication[J]. ACM Sigmobile Mobile Computing and Communications Review, 2001, 5(1): 3-55. |
| [14] |
O'brien R M. A Caution Regarding Rules of Thumb for Variance Inflation Factors[J]. Quality & Quantity, 2007, 41(5): 673-690. |
| [15] |
Chavez P S. Statistical Method for Selecting Landsat MSS Ratios[J]. Journal of Applied Photographic Engineering, 1982, 8(1): 23-30. |
| [16] |
Psilovikos A, Elhag M. Forecasting of Remotely Sensed Daily Evapotranspiration Data over Nile Delta Region, Egypt[J]. Water Resources Management, 2013, 27(12): 4115-4130. |
| [17] |
Sheffield C. Selecting Band Combinations from Multi Spectral Data[J]. Photogrammetric Engineering and Remote Sensing, 1985, 58(6): 681-687. |
| [18] |
基于GlobeLand30的全球城乡建设用地空间分布与变化统计分析[J]. 测绘学报, 2015, 44(11): 1181-1188. |
| [19] |
Vittinghoff E, Glidden D V, Shiboski S C, et al. Regression Methods in Biostatistics[M]. Boston: Springer, 2012.
|
| [20] |
Butler K. Band Combinations for Landsat 8[EB/OL]. (2013-07-24)[2022-02-22]. https://www.esri.com/arcgis-blog/products/product/imagery/bandcombinations-for-landsat-8/.
|
| [21] |
Potapov P, Hansen M C, Kommareddy I, et al. Landsat Analysis Ready Data for Global Land Cover and Land Cover Change Mapping[J]. Remote Sensing, 2020, 12(3): 426. |
| [22] |
Gong Peng, Liu Han, Zhang Meinan, et al. Stable Classification with Limited Sample: Transferring a 30 m Resolution Sample Set Collected in 2015 to Mapping10 m Resolution Global Land Cover in 2017[J]. Science Bulletin, 2019, 64(6): 370-373. |
| [23] |
Zhang Xiao, Liu Liangyun, Chen Xidong, et al. GLC_FCS30: Global Land-Cover Product with Fine Classification System at 30 m Using Time-Series Landsat Imagery[J]. Earth System Science Data, 2021, 13(6): 2753-2776. |
| [24] |
Yang Jie, Huang Xin. The 30 m Annual Land Cover Dataset and Its Dynamics in China from 1990 to 2019[J]. Earth System Science Data, 2021, 13(8): 3907-3925. |
| [25] |
Beauchemin M, Fung K O B. On Statistical Band Selection for Image Visualization[J]. Photogrammetric Engineering and Remote Sensing, 2001, 67(5): 571-574. |
 2022, Vol. 47
2022, Vol. 47


