| 基于改进的MROGH的特殊纹理航摄影像匹配 |
航摄影像通常包含大面积的荒漠、林地和耕地为内容的影像[1],在纹理上表现为贫乏纹理和重复纹理,这类影像称之为特殊纹理影像。由于贫乏纹理影像内容信噪比低[2],易受噪声干扰,匹配成功率低;重复纹理影像特性会导致描述符可区分性差,形成多个匹配,常用的影像匹配方法往往难以奏效[3]。
针对贫乏纹理影像,通常利用线特征来辅助影像匹配,例如线交叉上下文特征[4]、灭点方向引导的直线匹配[5, 6]、线段匹配(LSM)[7],但是线特征并不总是出现在航摄影像中。针对重复纹理影像,文献[8, 9]利用无人机数据处理海岛礁和道路边坡等地区,但是精度不足;文献[10]利用相位相关法辅助重复纹理区域影像匹配,获得数量足够且分布均匀的同名点;文献[11]提出基于图论的方法进行特殊航摄影像的匹配,匹配效果较好,但计算复杂度高无法投入实际生产中。文献[12]提出了MROGH(multi-support region order-based gradient histogram)匹配方法,在重复纹理影像中仍具有很好的独特性,但仅依靠灰度梯度向量还是会出现误匹配和匹配不均匀等情况[13]。
本文提出一种基于颜色不变量和MROGH的影像匹配方法。通过采用缩小搜索空间的匹配策略提高效率,采用最小二乘方法提高匹配精度。实验表明,本文提出影像匹配算法不仅能获取较多匹配点,而且具有较高的匹配正确率。
1 基本原理 1.1 颜色不变量基于特征的影像匹配方法通常只利用局部影像的灰度信息去构建描述符,忽略了彩色影像原有的颜色特征。本文研究在彩色影像上描述特征点的局部特征的方法,引入颜色不变量模型,Kubelka-Munk理论针对非透明物体提出了一种物体光谱辐射特性模型[14],可用式(1)表达:
| $ \begin{array}{c} E(\lambda, \vec{x})= \\ e(\lambda, \vec{x})\left(1-\rho_{f}(\vec{x})\right)^{2} R_{\infty}(\lambda, \vec{x})+e(\lambda, \vec{x}) \rho_{f}(\vec{x}) \end{array} $ | (1) |
式中,E为物体的反射光谱;λ为光谱波长;
| $ E(\lambda, \vec{x})=e(\vec{x})\left(\left(1-\rho_{f}(\vec{x})\right)^{2} R_{\infty}(\lambda, \vec{x})+\rho_{f}(\vec{x})\right) $ | (2) |
式(2)对于λ的一阶导数为:
| $ E_{\lambda}=e(\vec{x})\left(1-\rho_{f}(\vec{x})\right)^{2} \frac{\partial R_{\infty}(\lambda, \vec{x})}{\partial \lambda} $ | (3) |
二阶导数为:
| $ E_{\mu}=e(\vec{x})\left(1-\rho_{f}(\vec{x})\right)^{2} \frac{\partial^{2} R_{\infty}(\lambda, \vec{x})}{\partial \lambda^{2}} $ | (4) |
(E, Eλ, Eλλ)即为高斯颜色模型。根据式(3)和式(4)可以推导出颜色不变量H:
| $ H=\frac{E_{\lambda}}{E_{\lambda\lambda}}=\frac{\partial R_{\infty}(\lambda, \vec{x})}{\partial \lambda} / \frac{\partial^{2} R_{\infty}(\lambda, \vec{x})}{\partial \lambda^{2}}=f\left(R_{\infty}(\lambda, \vec{x})\right) $ | (5) |
对于彩色图像来说,通常用RGB(red-green-blue)三原色表示彩色空间。为了建立起RGB颜色空间和高斯颜色模型间的关系,引入CIE-1964-XYZ标准下的XYZ颜色空间[15]。根据CIE-1964-XYZ标准下的XYZ颜色分量和RGB颜色分量与高斯颜色模型之间的近似关系可以推导出高斯颜色模型和RGB颜色空间的关系:
| $ \left[\begin{array}{c} E \\ E_{\lambda} \\ E_{\mu} \end{array}\right]=\left[\begin{array}{rrr} 0.06 & 0.63 & 0.27 \\ 0.30 & 0.04 & -0.35 \\ 0.34 & -0.06 & 0.17 \end{array}\right]\left[\begin{array}{l} \mathrm{R} \\ \mathrm{G} \\ \mathrm{B} \end{array}\right] $ | (6) |
常用的旋转不变性是基于局部影像统计估计的方式,会导致许多正确匹配点没有被找到。MROGH算法避开了统计的方式,用特征点和周围采样点来生成旋转不变的坐标系,在此坐标系中生成的梯度自然是旋转不变的,在理论上能实现真正意义的旋转不变性。下面详细介绍坐标系生成方式和梯度计算方法。
如图 1所示,P是特征点,Pi是以特征点为中心支持区域内的采样点。为每个采样点建立平面坐标系,其中以Pi为原点,P到Pi连线方向定义为y轴方向,顺时针旋转和y轴正交的方向为x轴方向,则
| $ \left\{\begin{array}{l} D x\left(P_{i}\right)=H\left(P_{i}^{1}\right)-H\left(P_{i}^{3}\right) \\ D y\left(P_{i}\right)=H\left(P_{i}^{2}\right)-H\left(P_{i}^{4}\right) \end{array}\right. $ | (7) |
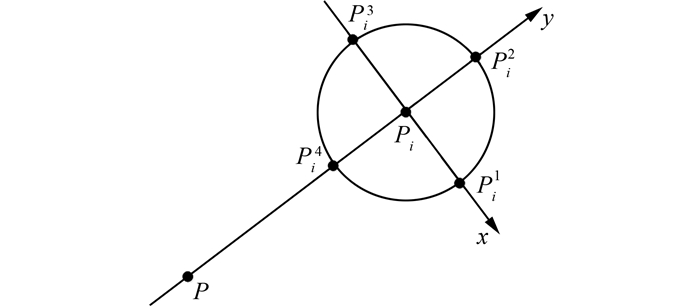 |
| 图 1 旋转不变的坐标系 Fig.1 Rotation-Invariant Coordinate System |
式中,Pij(j=1, 2, 3, 4)是采样点的支持区域与上述定义坐标系的坐标轴的交点;H(Pij)表示该点的颜色不变量值。此处采样点的梯度大小m(Pi)和梯度方向θ(Pi)可以定义为:
| $ \left\{\begin{array}{l} m\left(P_{i}\right)=\sqrt{D x\left(P_{i}\right)^{2}+D y\left(P_{i}\right)^{2}} \\ \theta\left(P_{i}\right)=\tan ^{-1}\left(D y\left(P_{i}\right) / D x\left(P_{i}\right)\right) \end{array}\right. $ | (8) |
按照式(8)为支持区域内的所有采样点生成旋转不变的梯度,并将梯度按照45°的距离加权等分成8个向量,然后按照颜色不变量把支持区域内的所有采样点排序,按序列等分成K份,最后每份区间中采样点的梯度被合并,这K份梯度向量共同组成这个支持区域的描述符。这种方式生成的梯度直方图不仅利用了采样点的局部彩色信息,还将特征点和采样点的关系、采样点之间的空间关系纳入其中,增加了描述符所包含的信息。这种方式生成的描述符是单一支持区域的,为了进一步提高描述符的独特性,本文根据MROGH多支持区域的原则,以特征点为中心等距离递增选用N个支持区域。同时也保证了描述符的尺度不变性。本文取N值为6。
1.3 影像匹配策略本文算法的描述符为192维,相较于传统的SIFT算法的描述符维数有所增加,所以在影像匹配时会增加计算量,消耗大量的匹配时间。为了提高本文算法的匹配效率,本文采用预测同名区域[3]的方法来缩小匹配过程中的搜索范围。匹配策略流程如图 2所示。具体做法是,首先对左右影像进行降采样,在其金字塔影像上进行初始匹配,利用匹配结果生成影像间的几何关系,达到利用少数点快速获得立体像对之间的单应矩阵的目的;然后在原始影像上提取特征,利用影像间的几何关系预测特征点在搜索影像上的同名范围,以达到减小特征匹配搜索范围、节省匹配时间的目的;接下来用本文改进的描述符的欧式距离作为匹配约束条件,在每个特征点的同名范围内进行特征匹配,再利用RANSAC算法进行误匹配点剔除工作;最后在匹配结果中应用最小二乘方法使匹配精度达到子像素级。
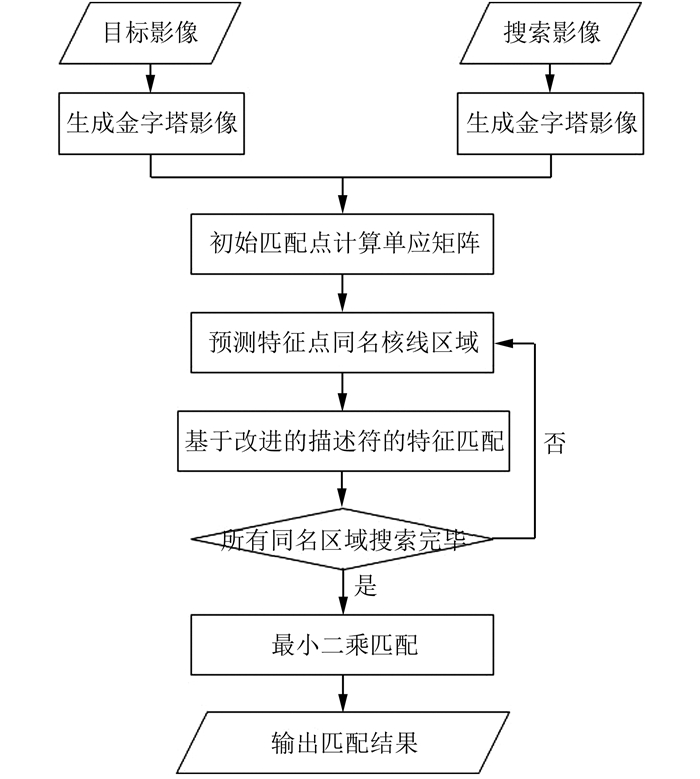 |
| 图 2 匹配策略流程图 Fig.2 Matching Strategy |
2 实验结果与分析 2.1 实验数据和定量评价指标
本文采取农田、林地和沙漠3组真实的特殊纹理影像数据,具体数据如表 1所示。采用C++语言在VS2010平台上实现匹配功能,计算机配置为CPU E5-1650 v3,64 GB内存,64位操作系统。
| 表 1 实验数据详细信息 Tab.1 Data Details |
 |
为定量评估本文匹配算法的先进性,分别从正确匹配点数量、匹配精度、匹配时间3个角度对匹配结果进行评估。实验中采用RANSAC方法剔除误匹配点后得到的匹配点集合可以认为是正确匹配点,但是匹配点的位置仍然存在误差,其误差计算式为:
| $ D=\sqrt{\frac{\sum\limits_{i=1}^{n}\left(\delta_{i}-\bar{\delta}\right)^{2}}{n}} $ | (9) |
式中,D为中误差;δi代表匹配点误差,δi=Xi-X′i;Xi为左影像上的匹配点变化到右影像上的坐标,X′i为右影像的坐标;n为匹配点数量;
改进的描述符中,采样点的等分份数是一个关键指标,为了找到本文算法所用描述符的最佳K值,本文分别选取10组特殊纹理立体影像对,测试在不同的K值下的影像匹配精度,测试结果如图 3所示。总体来说,随着K值的增加,匹配精度逐渐增高,而K=5时的匹配精度相较于K=4时的匹配精度并没有明显的提高。考虑到随着K值的增大,特征描述符的维度越大、匹配所消耗的时间也越多,所以综合考虑匹配精度和匹配效率这两方面的因素,本文取K值为4。
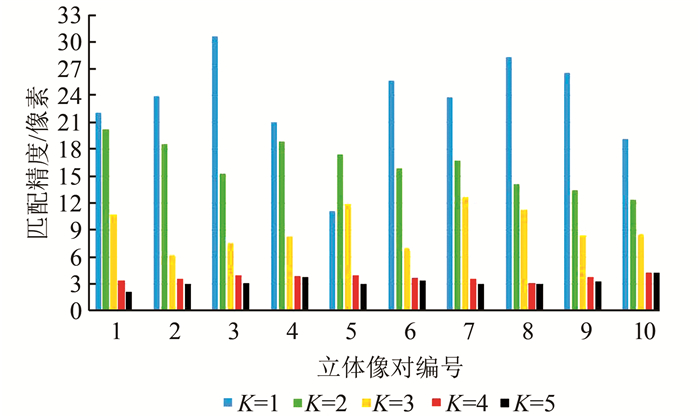 |
| 图 3 K值变化时匹配精度图 Fig.3 Matching Accuracy with Different K Values |
2.3 特殊纹理影像匹配实验 2.3.1 实验一
实验一选取了一组农田影像,匹配结果示意图如图 4所示,对于农田影像,SIFT(scale-invariant feature transform)算法提取到的匹配点很少,MROGH算法可以提取到大量的匹配点,但是匹配点主要聚集在图中绿色农作物覆盖的区域,而在枯萎的农作物区域和已经收割过的农作物区域,匹配到的同名点数量相对比较少,这种现象使得匹配点分布不均匀;本文算法得到的匹配点数量较多且在分布方面比较均匀,优于MROGH算法。表 2为实验结果,在匹配点数量方面,本文算法获得的匹配点最多,达到5 842对匹配点,这是由于本文方法引入了颜色不变量模型,充分利用了影像的颜色信息,对于影像中处于不同阶段不同颜色的农作物有很好的可区分性。在匹配精度方面,本文方法得到的匹配点精度达到了半个像素以内,明显优于前两种算法,MROGH算法得到的匹配点精度较差,这可能是MROGH算法得到的匹配点分布不均匀造成的。从匹配时间方面,MROGH算法匹配时间最多,这是因为它的描述符维数比较高。本文方法的匹配时间最少,虽然本文方法的描述符维数和MROGH相等,但本文在匹配搜索阶段通过预测同名区域的方法缩小搜索范围,节省了匹配时间。
 |
| 图 4 农田实验影像示意图 Fig.4 Matching Results with Farmland Image |
| 表 2 农田影像匹配结果统计表 Tab.2 Matching Result Statics with Farmland Image |
 |
2.3.2 实验二
实验二选取了一组林地影像,匹配结果示意图如图 5所示,SIFT算法几乎匹配不到同名点,MROGH算法得到的匹配点主要集中在图中裸露岩石区域和图像上方大面积浅绿色植被区域,匹配点分布不够均匀,这种情况的匹配点数量虽多,但是匹配点分布聚集,匹配效果仍然不理想;本文方法得到的匹配点数量比较多且分布比较均匀。表 3为实验结果,在匹配点数量方面,本文方法匹配到816对匹配点,数量最多且匹配点的分布情况相对更加均匀,说明本文方法的优势。在匹配精度方面,本文方法的匹配精度最优,可以达到0.56个像素。在匹配时间方面本文方法匹配时间和SIFT算法相似,小于MROGH算法。
 |
| 图 5 林地实验影像示意图 Fig.5 Matching Results with Forest Image |
| 表 3 林地影像匹配结果统计表 Tab.3 Matching Result Statics with Forest Image |
 |
2.3.3 实验三
实验三选取了一组沙漠影像,匹配结果示意图如图 6所示,3种方法在沙漠影像中可以提取到的匹配点都很少,匹配点多分布于沙漠的脊状纹理上,这主要是因为沙漠的纹理太单一,同名点间相似性太大,难以区分。比较来看SIFT算法和MROGH算法得到的匹配点只集中在影像的上方区域的沙脊上,本文算法比MROGH算法得到的匹配点要多,在影像的下方区域仍可以匹配到一些同名点。表 4为实验结果,本文方法可以匹配到430对同名点,明显多于前两种算法,这些匹配点大多分布于沙脊上,同时在沙坑位置也可以匹配到同名点,这是由于本文方法引入了颜色不变量,充分应用影像的颜色信息,避免了灰度梯度向量的混淆,可以表述像沙坑这种颜色有微小变化的区域的特征。在匹配精度方面本文的匹配精度优于前两种算法,保持在0.5个像素左右。从匹配时间方面,本实验和前两个实验相似。
 |
| 图 6 沙漠实验影像示意图 Fig.6 Matching Results with Desert Image |
| 表 4 沙漠影像匹配结果统计表 Tab.4 Matching Result Statics with Desert Image |
 |
3 结束语
本文在MROGH算法基础上引入颜色不变量模型,得到了结合影像的颜色信息和空间关系的局部描述符,提高了描述符的独特性;通过预测特征同名区域减少了匹配搜索空间,提高了匹配效率;通过最小二乘影像匹配方法提高了匹配精度。通过特殊纹理影像匹配对比实验表明,本文方法较MROGH和SIFT匹配方法能获取更多匹配点和更高的匹配精度。
| [1] |
钟灿. 非常规航摄影像定位方法及精度评定[D]. 武汉: 武汉大学, 2013
|
| [2] |
温久民, 韩健, 陈奕云. 喀斯特山区无人机摄影测量技术研究[J]. 测绘地理信息, 2018, 43(5): 32-34. |
| [3] |
袁修孝, 陈时雨, 张勇. 利用PCA-SIFT进行特殊纹理航摄影像匹配[J]. 武汉大学学报·信息科学版, 2016, 41(9): 1 137-1 144. |
| [4] |
Wu B, Zhang Y, Zhu Q. Integrated Point and Edge Matching on Poor Textural Images Constrained by Self-adaptive Triangulations[J]. ISPRS Journal of Photogrammetry and Remote Sensing, 2012, 68(1): 40-55. |
| [5] |
李畅, 刘亚文, 胡敏, 等. 面向街景立面三维重建的近景影像直线匹配方法研究[J]. 武汉大学学报·信息科学版, 2010, 35(12): 1 461-1 465. |
| [6] |
Li C, Zhang Y J, Zhang Z X. Automatic Keyline Recognition and 3D Reconstruction for Quasi-planar Facades in Close-Range Images[J]. The Photogrammetric Record, 2016, 31(153): 29-50. DOI:10.1111/phor.12141 |
| [7] |
Bay H, Ferrari V, Gool L V. Wide-Baseline Stereo Matching with Line Segments[C]. Computer Vision and Pattern Recognition, IEEE Computer Society Conference, San Diego, USA, 2005
|
| [8] |
谭金石, 黄书华, 黄正忠. 基于无人机遥感的海岛礁监测技术研究[J]. 测绘地理信息, 2018, 43(6): 55-57. |
| [9] |
周明, 邱凌云. 无人机技术在线路边坡病害巡查中的研究与应用[J]. 测绘地理信息, 2018, 43(4): 62-64. |
| [10] |
何海清, 张永军, 黄声享. 相位相关法辅助的重复纹理区低空影像匹配[J]. 武汉大学学报·信息科学版, 2014, 39(10): 1 204-1 207. |
| [11] |
Chen S, Yuan X, Yuan W, et al. Poor Textural Image Matching Based on Graph Theory[J]. ISPRS Journal of Photogrammetry and Remote Sensing, 2017, 129(7): 21-31. |
| [12] |
Fan B, Wu F, Hu Z. Rotationally Invariant Descriptors Using Intensity Order Pooling[J]. IEEE Transactions on Pattern Analysis and Machine Intelligence, 2012, 34(10): 2 031-2 045. DOI:10.1109/TPAMI.2011.277 |
| [13] |
梁焕青, 谢意, 付四洲. 颜色不变量与AKAZE特征相结合的无人机影像匹配算法[J]. 测绘学报, 2017, 46(7): 900-909. |
| [14] |
Gevers T, Smeulders A W M. Color Based Object Recognition[J]. Pattern Recognition, 1985, 18(3/4): 297. |
| [15] |
Geusebroek J M, Boomgaard R V D, Smeulders A W M, et al. Color Invariance[J]. IEEE Transactions on Pattern Analysis & Machine Intelligence, 2001, 23(12): 1 338-1 350. |
 2021, Vol. 46
2021, Vol. 46

