| 激光干涉测距技术在垂直控制网中布设研究 |
2. 水利部水工金属结构质量检验测试中心金属结构处,河南 郑州,450044;
3. 中国地质大学(北京)土地科学技术学院,北京,100083;
4. 海南省海洋地质调查研究院测绘室,海南 海口,570206
2. Metal Structure Office, National Center of Quality Inspection and Testing for Hydraulic Metal Structure, The Ministry of Water Resources, Zhengzhou 450044, China;
3. College of Land Science and Technology, China University of Geosciences(Beijing), Beijing 100083, China;
4. Surveying and Mapping Office, Marine Geological Survey Institute of Hainan Province, Haikou 570206, China
随着国家超高建筑的不断增加,垂直控制网的布设越来越重要。控制网作为工程施工的标准,在工程施工中起控制与约束的作用。传统测量方式在狭窄空间垂直控制网布设中存在多种局限。其中,经纬仪测量系统通过后方交会方式获取目标点的三维坐标,改善了传统测量方式测距精度远小于测角精度的弊端,但该测量方式人为误差较大、自动化程度低;全站仪测量系统通过测量空间距离、水平角度、垂直角度获取目标点的三维坐标,便携性好、自动化程度高,但在测量速度和精度方面仍难以满足某些特殊高精度测量任务要求[1]。全球导航卫星系统(global navigation satellite system,GNSS)定位精度高,测站间无需通视,可全天候工作,在国内海上风电等众多工程控制网布设中得到了广泛应用[2-8],但在精度要求较高、障碍物较多的工程中,存在信号较弱,控制位置难以到达的问题,不能满足测量要求。
激光跟踪测量系统的测角原理与全站仪类似[9],具有高精度、高效率、高自动化的特点。其在短距离测量中精度可达几十微米,是当前测量精度较高的测量系统之一,同时范百兴等[10]采用附有约束条件的参数平差方法构建了空间联合精密控制网平差模型,对多个联合测量系统进行平差解算,验证了该测量方式的平差模型可行性。激光跟踪仪凭借其高自动化测量模式,适用于高精度垂直控制网布设,被广泛应用于航空、航天、造船、汽车、机械制造、水电等工业测量领域[11-14],同时随着建筑物的增高,垂直控制网布设成为了主要方式。
三峡升船机为齿轮齿条爬升式垂直升船机,克服三峡水位落差大的问题,具有提升重量大、升程高、通航水位变幅大等特点,其水平和研究难度超过世界上许多通航升船机[15]。它是三峡水利枢纽的重要通航保障,极大促进了长江航运事业的发展[16]。因此在升船机的建设过程中,控制网布设的精度是重中之重。本文以三峡升船机建设中垂直控制网布设为研究对象,利用激光跟踪测量仪的短距离、高精度特性,模拟现场环境,对激光跟踪仪控制网布设精度进行研究,为200 m级三峡升船机的建设提供理论基础。
1 测量原理 1.1 激光跟踪仪测量原理激光跟踪仪在野外工作中具有较强的适用性,其测量模式为绝对测距模式。该系统通常按照右手坐标系获取目标点p在顺时针球坐标系(spherical clockwise system,SCW)下的位置,公式如下:
| $ \left\{\begin{array}{l} x=D \times \sin \beta \cos \alpha \\ y=D \times \sin \beta \sin \alpha \\ z=D \times \cos \beta \end{array}\right. $ | (1) |
式中,α、β、D分别表示水平角、天顶角、斜距。将式(1)进行线性化,按照误差传播定律计算得到p的精度误差。令水平角测角误差为mα,垂直角测角误差为mβ,两点之间的测距误差为mD,根据实际情况,水平角和垂直角测角误差相同,mα = mβ,则目标点位测量的中误差估计公式为:
| $ \left\{\begin{array}{l} m_x{ }^2=\sin ^2 \beta \cos ^2 \alpha \times m_D{ }^2+\left(\sin ^2 \beta \sin ^2 \alpha+\cos ^2 \beta \cos ^2 \alpha\right) \frac{D^2}{\rho^2} m_\beta{ }^2 \\ m_y{ }^2=\sin ^2 \beta \sin ^2 \alpha \times m_D{ }^2+\left(\sin ^2 \beta \cos ^2 \alpha+\cos ^2 \beta \sin ^2 \alpha\right) \frac{D^2}{\rho^2} m_\beta{ }^2 \\ m_z{ }^2=\cos ^2 \beta \times m_D{ }^2+\sin ^2 \beta \frac{D^2}{\rho^2} m_\beta{ }^2 \end{array}\right. $ | (2) |
式中,ρ为固定常数。将X、Y方向上的误差整理到水平面上可得:
| $ \left\{\begin{array}{l} m_{x y}{ }^2=m_x{ }^2+m_y{ }^2=\sin ^2 \beta \times m_D{ }^2+\frac{D^2}{\rho^2} m_\beta{ }^2 \\ m_p{ }^2=m_x{ }^2+m_y{ }^2+m_z{ }^2=m_D{ }^2+\left(1+\sin ^2 \beta\right) \frac{D^2}{\rho^2} m_\beta{ }^2 \end{array}\right. $ | (3) |
平面误差和整体误差都包含距离误差项和角度误差项,角度误差系数远大于距离误差系数。因此角度测量误差远大于距离测量误差,其中,测距中误差以固定误差给出,测角中误差以距离值的线性关系给出,在160 m测量范围内标称点位精度为±(15 μm+ 6 μm/m)。随着距离增加,测角误差越来越大,对点位精度的影响也越来越大,具体影响趋势见图 1。当垂直角小于π/4时,水平面方向精度误差较大,主要影响整体点位精度,而随着垂直角的增加,垂直方向误差占比越来越大,当达到3π/8时,水平面点位误差与垂直面点位误差共同影响整体点位误差精度。因此测量过程中根据测量要求选择合适的测量视角。
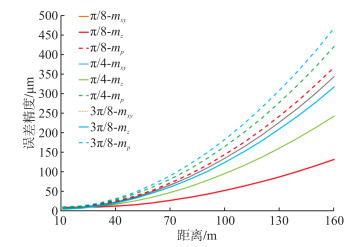 |
| 图 1 距离值对点位误差的影响 Fig.1 Influence of Distance Values on Point Position Errors |
1.2 测站三维平差模型解算
在垂直三维控制网中,设激光跟踪仪在第i个测站任意状态下的坐标系为
| $ \left\{\begin{array}{l} H_{i j}=2 {\rm{ \mathsf{π} }}-\arctan \frac{Y_{i j}}{X_{i j}} \\ V_{i j}=\frac{{\rm{ \mathsf{π} }}}{2}-\arctan \frac{Z_{i j}}{\sqrt{X_{i j}^2+Y_{i j}^2}} \\ S_{i j}=\sqrt{\left(X_j-X_i\right)^2+\left(Y_j-Y_i\right)^2+\left(Z_j-Z_i\right)^2} \end{array}\right. $ | (4) |
对
| $ \left\{\begin{aligned} V_{i j}{ }^S=& d_1 \delta X_{i 0}+d_2 \delta Y_{i 0}+d_3 \delta Z_{i 0}+d_4 \delta R_{x_i}+d_5 \delta R_{y_i}+\\ & d_6 \delta R_{z_i}+d_7 \delta X_j+d_8 \delta Y_j+d_9 \delta Z_j-l_{i j}{ }^S \\ V_{i j}{ }^H=& e_1 \delta X_{i 0}+e_2 \delta Y_{i 0}+e_3 \delta Z_{i 0}+e_4 \delta R_{x_i}+e_5 \delta R_{y_i}+\\ & e_6 \delta R_{z_i}+e_7 \delta X_j+e_8 \delta Y_j+e_9 \delta Z_{i j}-l_{i j}{ }^H \\ V_{i j}{ }^V=& f_1 \delta X_{i 0}+f_2 \delta Y_{i 0}+f_3 \delta Z_{i 0}+f_4 \delta R_{x_i}+f_5 \delta R_{y_i}+\\ & f_6 \delta R_{z_i}+f_7 \delta X_j+f_8 \delta Y_j+f_9 \delta Z_j-l_{i j}{ }^V \end{aligned}\right. $ | (5) |
式中,
| $ \boldsymbol{V}=\boldsymbol{A \delta_X}-\boldsymbol{l} $ | (6) |
式中,A表示系数矩阵;l表示自由项;δX =
设观测值权阵为P,按照最小二乘原理即可解算得到未知参数为:
| $ \boldsymbol{\delta_X}=\left(\boldsymbol{A}^{\mathrm{T}} \boldsymbol{P A}\right)^{-1} \boldsymbol{A}^{\mathrm{T}} \boldsymbol{P l} $ | (7) |
激光跟踪仪AT402全自动程度较高,在测量过程中通过自检校系统验证各控制点的测量精度,对于超限测点根据具体情况判定是否重测,图 2为激光跟踪仪在垂直控制网中的实验流程。
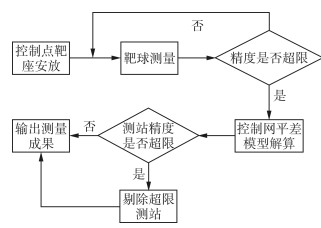 |
| 图 2 实验流程 Fig.2 Flow Chart of the Experiment |
2.2 实验内容
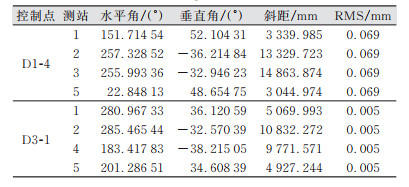
本文利用激光跟踪仪在垂直空间内进行控制网布设,并验证控制网中各控制点的布设精度,为200 m级三峡升船机控制网布设提供理论基础。针对垂直控制网的布设条件,本文选取水利部水工金属结构质量检测中心院内的启闭机实验平台进行实验,实验平台是一个长宽深均为10 m的凹井,周围实验机械设施均停止使用,无其他大型机械设施运行影响,在其内部侧壁上面共布设三层12个控制点,架设5站对控制点进行观测,保证每个控制点至少有3个测站可以观测到,其具体测站示意如图 3所示。所有控制点均分布在实验平台的垂直侧壁上,由于部分控制点位置不容易安放靶球,在测量时存在轻微移动现象,因此12个控制点经三角网平差解算之后,有3个控制点误差较大,严重影响控制网整体的测量精度和控制网的稳定性,因此,剔除控制点D2-2等3个控制点,对剩余9个控制点重新进行三角网平差解算,得到的均方根(root mean square,RMS)数据见表 1,控制点最大误差为0.069 mm。
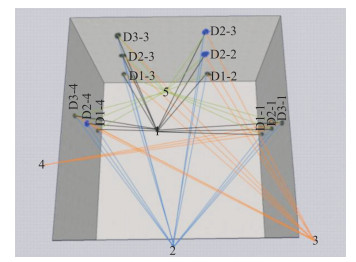 |
| 图 3 控制点布设测量示意图 Fig.3 Layout Survey Diagram of Control Points |
| 表 1 测量控制点解算数据/mm Tab.1 Solution Data of Measurement Control Points/mm |
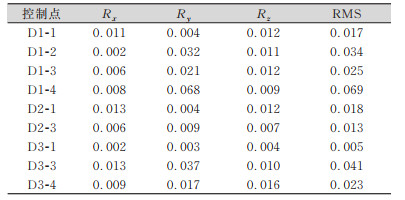 |
根据表 1,在X、Z方向上的测量误差变化较小,而Y方向上的测量精度误差波动较大,其间接影响了点位整体的测量误差。其中,控制点D3-1测量精度最高,仅有5 μm的点位误差,而控制点D1-4整体测量误差较大,远高于其他控制点的测量误差。
如表 2所示,控制点D1-4测量垂直角在测站1和测站5处大于45°,增大了整体点位的精度误差,而控制点D3-1的4个测站角度均小于45°,使该控制点的整体测量精度较高。因此,垂直角增加会增大控制点的整体精度误差。由于目标点三维坐标是根据激光跟踪仪测量的角度和距离计算出来的,对比各控制点的解算距离和实际测量距离同样可以检验各点位的测量精度,其测量距离与解算距离差值见图 4。大部分控制点的点位误差较稳定,在±0.06 mm间浮动,完全符合200 m级三峡升船机施工的测量精度要求。
| 表 2 点位原始数据 Tab.2 Original Point Data |
 |
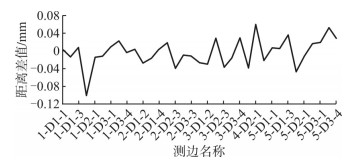 |
| 图 4 平差后解算距离与解算距离的差值 Fig.4 Difference Between Solution Distances and Solution Distances After Adjustment |
3 结束语
本文以模拟实验环境为例,验证激光跟踪仪在垂直控制网中的布设精度,证明了激光跟踪仪能够满足亚毫米级的高精度控制网布设任务。同时激光跟踪仪无需人工照准,可视范围水平方向无死角,垂直方向观测角可达135°,能够适用于大型耸立建筑的垂直控制网布设环境,为200 m级三峡升船机的布设提供了稳定的解决方案。
| [1] |
杨凡. 高能粒子加速器工程精密测量研究[D]. 郑州: 信息工程大学, 2011
|
| [2] |
黄丁发, 张勤, 张小红. 卫星导航定位原理[M]. 武汉: 武汉大学出版社, 2015.
|
| [3] |
张靖. 海上风电工程GNSS控制网建立方法研究[J]. 人民长江, 2021, 52(4): 153-156. |
| [4] |
张勤, 黄观文, 王利, 等. GPS在西安市地面沉降与地裂缝监测中的应用研究[J]. 工程地质学报, 2007, 15(6): 828-833. DOI:10.3969/j.issn.1004-9665.2007.06.019 |
| [5] |
张国强. GPS定位技术在精密工程测量中的应用研究[J]. 测绘与空间地理信息, 2006, 29(2): 41-42. DOI:10.3969/j.issn.1672-5867.2006.02.012 |
| [6] |
吴迪军, 熊伟, 郑强. 港珠澳大桥首级控制网复测方法研究[J]. 工程勘察, 2011, 39(9): 74-78. |
| [7] |
李凯锋, 欧阳永忠, 陆秀平, 等. 基于PPP技术的海岛礁平面控制测量应用实践[J]. 武汉大学学报·信息科学版, 2015, 40(3): 412-416. |
| [8] |
宋丽琴. 西江四等GPS平面控制网的布测[J]. 哈尔滨师范大学自然科学学报, 2015, 31(3): 70-74. DOI:10.3969/j.issn.1000-5617.2015.03.022 |
| [9] |
李广云, 李宗春. 工业测量系统原理与应用[M]. 北京: 测绘出版社, 2011.
|
| [10] |
范百兴, 李广云, 周维虎, 等. 激光跟踪仪空间联合平差模型及精度分析[J]. 武汉大学学报·信息科学版, 2018, 43(1): 120-126. |
| [11] |
马骊群. 大尺寸计量校准技术研究及在量值传递中的应用[D]. 大连: 大连理工大学, 2007
|
| [12] |
于成浩, 柯明, 赵振堂. 激光跟踪仪测量精度的评定[J]. 测绘工程, 2006, 15(6): 39-42. |
| [13] |
周维虎, 费业泰, 李百源, 等. 激光跟踪仪几何误差修正[J]. 仪器仪表学报, 2002, 23(1): 56-59. |
| [14] |
刘万里, 曲兴华, 欧阳健飞, 等. 激光跟踪测量系统角度自动校正装置设计[J]. 光学精密工程, 2008, 16(9): 1 695-1 700. |
| [15] |
邱章云, 罗琛. 三峡升船机塔柱施工期变形监测[J]. 中国工程科学, 2013, 15(9): 102-107. |
| [16] |
赵锡锦. 三峡升船机工程建设综述[J]. 中国工程科学, 2013, 15(9): 9-14. |
 2022, Vol. 47
2022, Vol. 47


