| 一种联合WiFi信息和PDR算法的智能手机室内定位方法 |
2. 广州汽车集团股份有限公司汽车工程研究院,广东 广州,511434
2. Automotive Research & Development Center, Guangzhou Automobile Group Co., Ltd., Guangzhou 511434, China
在室内场景中,由于建筑物的遮挡、室内结构复杂,全球导航卫星系统(global navigation satellite system,GNSS)常受到信号干扰,难以提供精确的定位导航信息。因此,实现室内环境定位服务显得尤为重要。为达到这一目标,研究人员提出了许多室内定位技术,如ZigBee定位[1]、射频识别技术[2]、红外定位[3]、超声波定位[4]、超宽带无线电技术[5]、WiFi定位[6]、航位推算定位[7]、地磁定位[8]等。这些定位技术都存在各自的优缺点,使用场景也各有不同,至今没有一种通用的室内定位技术大范围推广。
手机上集成了加速度计、陀螺仪、磁力计等多种传感器,这使得利用手机进行航位推算成为可能[9]。同时,由于WiFi的普及,如商场、机场等室内环境大多分布了覆盖率较高的WiFi,基于手机WiFi的定位方式成为一种热门的室内定位方案。WiFi定位的成本较低,但精度易受环境影响;行人航位推算(pedestrian dead reckoning,PDR)定位精度不受外界影响,但只能获取相对位置,且存在累计误差。故本文提出联合WiFi指纹定位和PDR算法的室内定位方法。
1 方法原理与流程 1.1 手机WiFi指纹定位算法WiFi指纹定位利用多个WiFi热点在定位环境中形成具有唯一性的信号强度序列进行定位。这种信号强度序列被称为WiFi指纹。整个定位技术包含训练和服务两个阶段。训练阶段主要包括WiFi指纹的采集与处理、定位模型的确定;服务阶段是指利用手机WiFi模块和定位模型确定手机位置的过程。
1)构建WiFi指纹地图。实地采集指定WiFi热点设备的接收信号强度(received signal strength,RSS)值,得到WiFi指纹。同时记录该位置的空间信息,如平面坐标、楼层等,即可得到WiFi指纹地图。
图 1展示了某一地点RSS值的分布与高斯模型。同一位置不同WiFi热点的信号强度分布类似高斯分布,用采集到的数据构建高斯模型,并用高斯模型选出高概率数据,对这些数据求平均值,将其作为各个位置的每个热点滤波后的信号强度值,再录入指纹地图数据库,减少异常信号数据对定位结果的影响[10]。
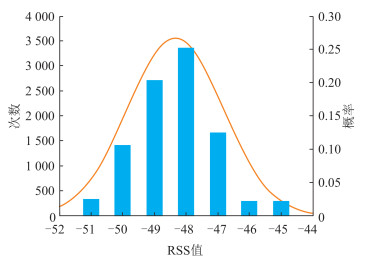 |
| 图 1 RSS值分布与高斯模型 Fig.1 Distribution of RSS Values and Gaussian Model |
2)建立WiFi指纹匹配算法。利用WiFi指纹进行定位起源于RADAR算法[11],该算法使用k最近邻(k-nearest neighborhood,KNN)算法去推断用户位置。将定位时采集到的信号向量与指纹地图数据库中的数据进行比较,选出相似度最接近的一个或多个WiFi指纹,综合这些指纹的位置信息,便可得到WiFi定位的估计位置。
KNN是当前最常见的匹配算法,该算法直接计算采集的信号向量与指纹向量的欧氏距离,等同对待每个指纹对定位结果的贡献。加权KNN(weighted KNN,WKNN)算法在定位过程中,不仅能计算出前k个欧氏距离最小的指纹向量,还能对不同指纹位置设置不同的权重,这k个位置的平均值计算公式如下:
| $ \mathop x\limits^ \rightharpoonup=\sum\limits_{i=1}^{k} \omega_{i} {{\overset{\rightharpoonup }{\mathop{x}}}_{i}} $ | (1) |
式中,
| $\omega_{i}=\frac{1}{d_{i}} / \sum\limits_{i=1}^{k} \frac{1}{d_{i}} $ | (2) |
式中,di为向量的欧氏距离。
当前指纹向量与手机采集的信号向量间的欧氏距离越小,该指纹的重要性权重就越大。由于每个指纹对定位结果的贡献不同,而不能等同对待。本文用WKNN算法来实现手机WiFi指纹定位。
1.2 基于手机传感器的PDR算法PDR算法通过将体积小、精度低的惯性传感器固定在行人身上,检测行人步数、步长、步行方向,从而实现位置推算[12]。
利用手机加速度计的数据分析行人步行状态,实现步伐检测,根据一步过程中的加速度特征,使用步长估算模型计算行人步行距离,再结合手机的加速度计和磁力计算出步行方向。于是,在每一步结束的时刻,可以根据步长和方向计算步行相对坐标,再不断递推,最终达到行人定位的目的。因此,手机PDR算法的核心在于步伐检测、步长估计、方向角确定3个方面。
1)步伐检测。手机步伐检测采用的传感器是手机加速度计,对手机加速度计的数据进行预处理,可将步伐检测问题转化为加速度变化周期检测问题。
本文采用的是改进的峰值检测法。人在行走过程中,行走的速度会影响到加速度变化周期,而手机的无规律抖动,或步行过程中使用手机,会导致加速度中出现一些伪波峰,如图 2所示。
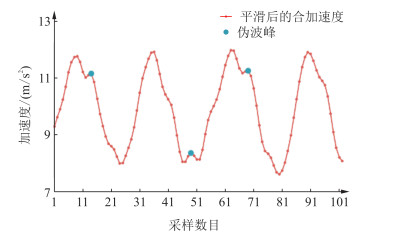 |
| 图 2 伪波峰现象 Fig.2 Pseudo Crest Phenomenon |
手机开启加速度监听后,不断采集加速度数据,对于原始加速度数据,需要对其合加速度进行均值滤波,再进行峰值检测。检测到峰值后需要计算3个特征值,分别是相邻波峰时间间隔、波峰的加速度值、两个波峰的差值,只有这3个特征值同时满足阈值约束时,才能判定行人当前已行走一步。
2)步长估计。非线性模型主要通过对人步行过程中的加速度观测值采用统计分析方法建立数学模型。Weinberg[13]提出了一种简单的非线性模型:
| $ S \approx \sqrt[4]{A_{\max }-A_{\min }} \times a $ | (3) |
式中,S为行人步长;Amax、Amin分别代表一步过程中Z轴方向的最大、最小加速度;a为常量,代表模型系数。
人在正常行走时,速度的变化不会太大,在整体上是一个渐变的过程,这个过程中前后两步之间的步长虽然不同,但差异不大,因此可以在非线性步长估算的基础上对每一步进行微调。本文采用卡尔曼滤波对非线性步长估计模型进行改进。
在步长估算中,将t时刻每一步的步长作为系统状态xt,则系统变化规律可用以下线性状态方程描述:
| $x_{t}=\boldsymbol{F}_{t} x_{t-1}+B_{t} \boldsymbol{u}_{t}+w_{t} $ | (4) |
式中,Ft表示系统从t-1时刻演化到t时刻的状态转移矩阵;Bt是作用在控制器向量ut上的输入,即控制模型;wt是过程噪声,并服从N(0,Q) 分布。令Ft=1,即令前后两步步长相等,由于系统没有控制输入,所以不存在Btut项,则wt的意义就是前后两步的步长变化。
将非线性步长估算模型的计算结果作为系统的观测zt,观测值与系统状态值之间的关系可以用线性测量方程表示:
| $ z_{t}=\boldsymbol{H}_{t} x_{t}+v_{t} $ | (5) |
式中,Ht为测量矩阵;vt为观测噪声,服从N(0,Q) 分布,且与过程噪声互不相关。
由于Weinberg模型需要事先确定各自的模型系数a,所以在实验前,在走廊中正常行走100 m,利用步伐检测计算步数,根据每一步的加速度特征计算a。图 3展示了步长估计结果,可以看出,使用卡尔曼滤波对非线性模型进行改进后,步长估计结果比原模型算法的结果更加稳定、准确。
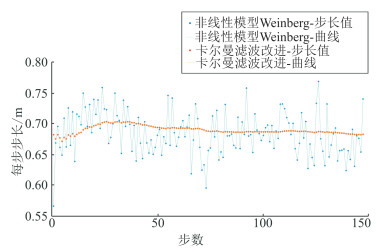 |
| 图 3 基于卡尔曼滤波的步长估计 Fig.3 Step Estimation Based on Kalman Filter |
3)方向角确定。本文利用手机中陀螺仪和电子罗盘数据,采用互补滤波器进行方向角确定。
1.3 PDR定位结果纠正考虑到行人行走具有连续性,并且始终在当前位置可达的区域行走,需要利用地图结构纠正PDR计算结果。在融合地图信息时,可以使用粒子滤波算法对行人运动特征进行约束,对处于不可达的区域的粒子,将其权值降低,使得位置估计更准确。
粒子滤波算法通过寻找一组在状态空间中传播的样本来近似表示概率密度函数[14],用样本均值代替积分运算,进而获得系统状态最小方差估计。
在本文PDR算法中,算法的输入为手机加速度A、磁场强度M、上一时刻位置xt-1,算法输出为当前位置xt,则系统的状态方程可以表达为如下形式:
| $ x_{t}=\boldsymbol{F}\left(x_{t-1}, A, M\right) $ | (6) |
对于粒子滤波中的每一个粒子,在计算其重要性权值时,可以使用如下重要性密度函数:
| $ p\left(z_{t} \mid x_{t}^{i}\right)=\frac{1}{2 {\rm{ \mathsf{ π}}}} \mathrm{e}^{-\frac{\left(x_{t}-x_{t}^{i}\right)^{2}}{2 \sigma^{2}}} $ | (7) |
式中,σ为位置估计标准差;xt为利用上一时刻位置估算结果进行预测的位置;xti为利用上一时刻第i个粒子的位置进行预测的结果,两者都由式(6)计算。由于整个粒子群的初始化是在初始位置附近采样,后续定位计算中可能出现部分粒子的预测结果与上一时刻的位置形成“穿墙而过”的现象,因此需要对这一类粒子的权重进行抑制。如图 4所示,图中黑色圆点为上一时刻位置估算结果,上方粒子和下方粒子为粒子群的预测位置,由于图中上方粒子与上一步位置估算结果的连线与墙相交,则认为这部分粒子的预测结果不合理,将其重要性权重降低。
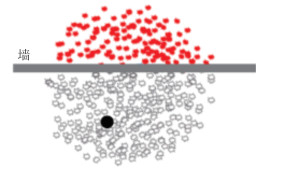 |
| 图 4 粒子权重抑制示意图 Fig.4 Diagram of Particle Weight Suppression |
本文利用PostgreSQL空间查询插件PostGIS中的ST_Intersects函数完成“穿墙”检测。基于这一思路,每个粒子的重要性权值wt(xti)的递推更新公式可表示为如下形式:
| $ w_{t}\left(x_{t}^{i}\right)=\left\{\begin{array}{l} \tilde{w}_{t}\left(x_{t-1}^{i}\right) p\left(z_{t} \mid x_{t}^{i}\right), \text { 正常粒子 } \\ 0.01 \tilde{w}_{t}\left(x_{t-1}^{i}\right) p\left(z_{t} \mid x_{t}^{i}\right), \text { 穿墙粒子 } \end{array}\right. $ | (8) |
式中,
在PDR算法中应用粒子滤波时,有大量的粒子参与计算,造成粒子少时算法不稳定、粒子多时算法效率低两个弊端。为了能得到一种稳定的、能用于实时定位的算法,本文在标准粒子滤波算法的基础上提出了一种简化的粒子滤波算法。
首先,粒子数量过多导致算法时间复杂度较高,而在实际运算过程中,粒子不可避免地会发生权重衰减,大部分粒子的权重都非常低,它们却使得数据库交互次数大大增加。为了降低计算成本,本文采用25个粒子进行递推计算。这25个粒子在初始化时,以当前定位位置为中心,往X、Y方向以1 m为间隔形成一个5 × 5大小的点阵,如图 5所示,图中黑点为当前位置。每次初始化或重采样时都按照这种规则设置粒子,避免随机采样导致算法性能不稳定的问题。
 |
| 图 5 粒子分布示意图 Fig.5 Diagram of Distribution of Particles |
其次,采用的粒子数量只有25个,对其进行加权求和运算并不能逼近贝叶斯滤波中的积分运算,得到的计算结果与实际位置间会存在较大偏差。因此,在利用粒子估算当前时刻位置时,本文没有采用粒子位置的加权和进行计算,而是直接使用重要性权值最大的粒子的位置作为本次定位优化结果。这会使得定位轨迹尽量保持原始PDR定位轨迹的原貌。而在标准粒子滤波算法中,由于加权和受到很多粒子的影响,会对每一步的定位结果都进行修改,比如在走廊中靠墙行走时,标准粒子滤波算法会使轨迹更加靠近走廊中间。使用简化的粒子滤波算法,粒子对轨迹的影响不大,当轨迹发生“穿墙”现象时,重要性权值最大的粒子会对定位结果进行改正。
除了以上两点简化操作,其他步骤如重要性权值更新、粒子退化检测等都与粒子滤波算法保持一致。针对PDR算法,采用简化粒子滤波算法后的计算结果如图 6所示,图中的轨迹与原PDR算法计算的轨迹基本一致,在原PDR轨迹第一次发生“穿墙”现象的位置,图中的轨迹有明显的不连续“跳动”,避免了定位结果落入不可达区域,这就是由权值最大的粒子对定位结果进行改正的结果。
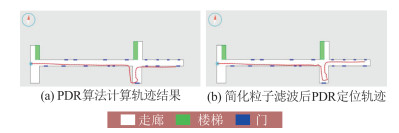 |
| 图 6 采用简化粒子滤波前后的轨迹 Fig.6 Trajectories Before and After Using Simplified Particle Filter |
2 手机室内定位系统实现和实验分析 2.1 系统实现
本文室内定位系统包含3个部分:手机客户端、服务器端和WiFi基站。系统采用的是客户端-服务器(client/server,C/S)和浏览器-服务器(browser/ server,B/S)混合结构模式。其中,在训练阶段完成WiFi指纹地图构建和定位算法的确定。服务阶段中服务器端使用PDR定位模块和WiFi定位模块计算出定位结果并将其返回手机端,手机端获取定位结果后会更新到手机界面的地图上。
2.2 实验分析本文以武汉大学信息学部5号楼的一楼和二楼为实验区域进行了一组行人定位实验。实验所在走廊面积约190 m2,东西方向的走廊长约62 m,宽约2.5 m;南北方向的走廊长约15 m,宽约3.7 m,实验设备为红米4手机。
首先构建WiFi指纹地图,沿着实验区域的走廊中间位置,以1 m为间隔采集了62个位置的WiFi指纹,每个位置指纹约有50个WiFi热点信号,在每个位置采集信号的时间约5 min,采集的次数为10 000次。将处理后的WiFi指纹与位置信息一同存入数据库,每个位置都对应唯一的WiFi指纹信息。
实验过程中,行人手持实验设备从5号楼正门出发,沿一楼走廊直行后上楼梯到二楼,并继续直行,整个轨迹长约110 m。为了得到系统的定位精度,行人在行走过程中选择5个地点作为对比点,记录该位置的实际坐标和定位结果。对比点1、2、3、4、5的定位误差分别为1.80 m、0.78 m、1.89 m、1.43 m、2.44 m。
真实轨迹及对比点分布见图 7。由图 8定位轨迹可以发现,步行方向的稳定对于PDR算法尤为重要。图 7(a)中,在上楼过程中手机抖动剧烈,手机检测到的方向角存在较大误差,因此,楼梯部分定位结果与实际轨迹偏差较大。此外,由于对比点1附近方向检测的噪声较大,轨迹方向与实际情况偏差较大。在该处转弯时,PDR算法发生了“穿墙”,而本文采用的简化粒子滤波算法能在“穿墙”点附近找到一个合适的定位结果,从而保证PDR算法的正常递推。在对比点3附近,由于WiFi定位模块检测到楼层发生切换,使得PDR算法重新设置初始位置,并在二楼进行递推计算。
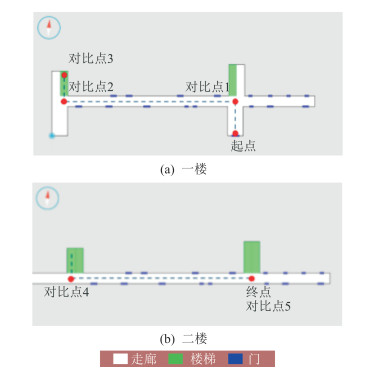 |
| 图 7 真实轨迹及对比点分布 Fig.7 Real Trajectories and Distribution of Contrast Points |
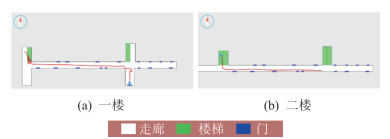 |
| 图 8 系统定位结果 Fig.8 System Positioning Results |
5个对比点误差都在3 m以内,误差最大的是在二楼中对比点5,由于行人到达该点时经历了一段较长距离的直行,误差不断积累,最终达到2.44 m。因此在长距离直行时,由于无法有效地融合地图结构信息,PDR算法的误差无法及时降低。而在一楼的对比点1使用粒子滤波纠正“穿墙”结果后,在对比点2处的误差有一定降低,只有0.78 m。
3 结束语本文使用的简化粒子滤波融合地图信息能有效降低PDR算法的累积误差,而WiFi指纹定位既能为PDR算法提供初始值,又能检测楼层切换,从而实现定位系统的跨楼层定位,使得室内定位系统的适应性更强,为其他室内联合定位方案提供了参考。
| [1] |
Goncalo G, Helena S. Indoor Location System Using ZigBee Technology[C]. 2009 Third International Conference on Sensor Technologies and Applications, Athens, Greece, 2009
|
| [2] |
Ni L M, Liu Y H, Lau Y C, et al. LANDMARC: Indoor Location Sensing Using Active RFID[C]. Proceedings of the First IEEE International Conference on Pervasive Computing and Communications, Fort Worth, TX, USA, 2003
|
| [3] |
Kemper J, Linde H. Challenges of Passive Infrared Indoor Localization[C]. 2008 5th Workshop on Positioning, Navigation and Communication, Hannover, Germany, 2008
|
| [4] |
Hazas M, Hopper A. Broadband Ultrasonic Location Systems for Improved Indoor Positioning[J]. IEEE Transactions on Mobile Computing, 2006, 5(5): 536-547. DOI:10.1109/TMC.2006.57 |
| [5] |
Ingram S J, Harmer D, Quinlan M. UltraWideBand Indoor Positioning Systems and Their Use in Emergencies[C]. Position Location and Navigation Symposium, Monterey, CA, USA, 2004
|
| [6] |
le Dortz N, Gain F, Zetterberg P. WiFi Fingerprint Indoor Positioning System Using Probability Distribution Comparison[C]. 2012 IEEE International Conference on Acoustics, Speech and Signal Processing, Kyoto, Japan, 2012
|
| [7] |
Judd T. A Personal Dead Reckoning Module[C]. 10th International Technical Meeting of the Satellite Division of the Institute of Navigation, Kansas City, USA, 1997
|
| [8] |
徐亮. 基于地磁导航的室内定位算法研究与实现[D]. 南京: 南京邮电大学, 2015
|
| [9] |
陈春阳, 郭英, 毕京学. 手机陀螺仪与加速度计联合定位初步分析[J]. 导航定位学报, 2014, 2(4): 74-77. |
| [10] |
薛卫星, 邱卫宁, 花向红, 等. RSSI信号特征值对WiFi室内定位精度的影响分析[J]. 测绘地理信息, 2016, 41(4): 23-26. |
| [11] |
Bahl P, Padmanabhan V N. RADAR: An In-Building RF-Based User Location and Tracking System[C]. Conference on Computer Communications. Nineteenth Annual Joint Conference of the IEEE Computer and Communications Societies, Tel Aviv, Israel, 2000
|
| [12] |
张鹏, 赵齐乐, 李由, 等. 基于PDR、WiFi指纹识别、磁场匹配组合的室内行人导航定位[J]. 测绘地理信息, 2016, 41(3): 29-32. |
| [13] |
Weinberg H. Using the ADXL202 in Pedometer and Personal Navigation Applications[J]. Analog Devices AN-602 Application Note, 2002, 2(2): 1-6. |
| [14] |
魏国华. 粒子滤波算法研究与实现[D]. 成都: 电子科技大学, 2015
|
| [15] |
王法胜, 鲁明羽, 赵清杰, 等. 粒子滤波算法[J]. 计算机学报, 2014, 37(8): 1 679-1 694. |
 2022, Vol. 47
2022, Vol. 47

