| 基于传统超宽带的室内高精度动态定位算法 |
2. 深圳大学信息工程学院,广东 深圳,518060;
3. 武汉大学测绘遥感信息工程国家重点实验室,湖北 武汉,430079
2. College of Information Engineering, Shenzhen University, Shenzhen 518060, China;
3. State Key Laboratory of Information Engineering in Surveying, Mapping and Remote Sensing, Wuhan University, Wuhan 430079, China
随着无线通信技术的发展以及移动通信和无线传感器网络的普及,全球导航定位技术日趋成熟。室外条件下,全球定位系统(global positioning system, GPS)是人们普遍采用的定位解决方案,在没有外部设备辅助情况下,其定位精度可达10 m以内。然而在室内环境中,由于传播环境更为复杂,无线传播信道受到的干扰使得室内定位的难度随之增加。与此同时,由于室内定位在商业、公共安全以及军事方面的巨大应用,基于位置的服务正在成为人们生活和工作中不可或缺的一部分。因此如何稳定、实时地提供精准的位置信息成为了目前研究的热点。
现行的室内定位解决方案众多,如WiFi(wireless fidelity)指纹定位、蓝牙定位、红外线定位、射频识别(radio frequency identification,RFID)定位以及超宽带(ultra-wideband,UWB)定位等。其中,UWB技术凭借传输速率高、结构简单、功耗小、穿透力强以及良好的抗多径性能等优点,在短距离无线通信领域、定位和跟踪领域有着非常广阔的应用前景。相比其他技术,UWB更适用于室内环境下的精准定位,目前基于UWB传感器的室内定位系统可以达到cm级的定位精度。
近些年来,许多文章开始深入分析UWB等技术在室内定位中的应用[1-3]。这些研究中,大多数集中于从UWB的信道模型和测距误差角度来提高室内定位精度,文献[4, 5]分析了UWB技术在多径环境中的传播模式以及性能;Dardari等[6]结合到达时间(time of arrival, TOA)的方法研究了UWB信号在多径环境下的测距精度,然而基于TOA的方法对于系统有很高的时钟同步要求,实际应用中很难达到;而文献[7, 8]则通过到达时间差(time difference of arrival, TDOA)的方法降低了室内定位系统对时钟同步的要求,同时提升了定位精度。Kolakowski等提出了协同定位的改进算法,将双边两路测距(double-sided two-way ranging,DS-TWR)和TDOA结合[9],基于最小二乘和Taylor级数展开[10-12]来进一步实现室内条件下的精准定位。
上述算法并未顾及目标的运动信息,定位模型没有考虑目标在一组观测时间内的位置变化,对动态运动进行定位时会带来较大的误差,无法满足对精度和实时性有较高要求的应用场景。本文提出了一种引入速度参数的UWB室内定位算法,并根据先验知识对目标的位置观测和速度估计进行约束,从而实现对运动目标的高精度定位。
1 定位系统及原理UWB室内定位系统由一组观测锚节点和移动标签组成,其架构如图 1所示。移动标签通过UWB将测距信息发送到观测锚节点并记录发送时间,观测锚节点接收传送的信息并记录信息到达的时间,通过这种方式,观测锚节点和移动标签之间进行信息传输和交流,并将记录的信息用于测距计算。为消除UWB设备的时钟晶振频率漂移对测距精度的影响,本文采用的DS-TWR测距原理如图 2所示。
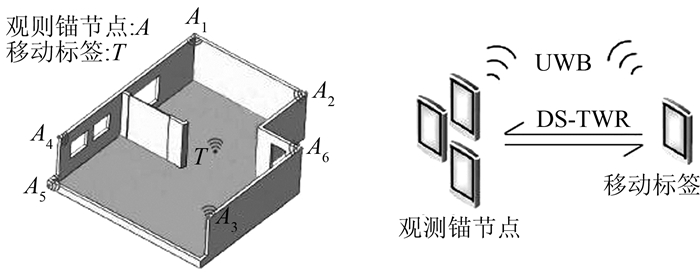 |
| 图 1 UWB室内定位系统 Fig.1 UWB Indoor Localization System |
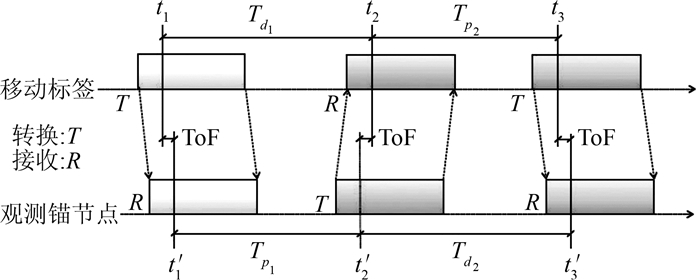 |
| 图 2 双边两路测距 Fig.2 Double-Sided Two-Way Ranging |
移动标签发起第一次往返测量,并由观测锚节点进行响应;同理观测锚节点发起第二次往返测量,并由移动标签进行响应,这样就完成了一个完整的DS-TWR交换过程。
每个设备精确的记录下发送和接收消息的时间戳。则消息在设备间飞行时间Tf可以表示为:
| $ {T_f} = \frac{{{T_{{d_1}}} \times {T_{{d_2}}} - {T_{{p_{_2}}}} \times {T_{{p_{_1}}}}}}{{{T_{{d_1}}} + {T_{{d_2}}} + {T_{{p_{_1}}}} + {T_{{p_2}}}}} $ | (1) |
式中,Td1=t2-t1; Td2=t′3-t′2; Tp1=t′2-t′1; Tp2=t3-t2。则
| $ d = c \times {T_f} $ | (2) |
式中,c为真空中的光速。
由于UWB测距设备自身时钟晶振频率漂移造成的Tf计算误差e误差为:
| ${e_{误差}} = \frac{1}{2}{T_f}\left( {{e_T} - {e_A}} \right)$ | (3) |
式中, eT、eA分别为移动标签和观测锚节点对应的时钟频率漂移,一般情况下取值为2 × 10-6~40× 10-6。
采用式(1)计算Tf的方式,可以获得更为精确的测距结果,即使在100 m的测距环境下,由设备时钟晶振频率漂移造成的测距误差仅为2.2 mm。
2 顾及速度参数的UWB室内定位算法在上述UWB室内定位系统中,观测锚节点i的坐标为(xi,yi, zi),i=1, 2, 3,…,N,移动标签的坐标为(x, y, z),则移动标签与观测锚节点i可建立观测方程为:
| ${d_i} = \sqrt {{{\left( {x - {x_i}} \right)}^2} + {{\left( {y - {y_i}} \right)}^2} + {{\left( {z - {z_i}} \right)}^2}} $ | (4) |
式中,di为移动标签与观测锚节点i通过DS-TWR得到的观测距离。
根据一组观测锚节点的观测,可以列出观测方程组,求得运动目标的位置。由于上述方程为非线性方程求解困难,本文将采用Taylor级数展开法线性化观测方程,通过加权最小二乘法实现对目标位置的精确估计。观测锚节点i和观测锚节点1与移动标签之间观测距离的差di, 1为:
| $ \begin{array}{*{20}{c}} {{d_{i, 1}} = {d_i} - {d_1}{\rm{ = }}}\\ {\sqrt {{{\left( {x - {x_i}} \right)}^2} + {{\left( {y - {y_i}} \right)}^2} + {{\left( {z - {z_i}} \right)}^2}} - }\\ {\sqrt {{{\left( {x - {x_1}} \right)}^2} + {{\left( {y - {y_1}} \right)}^2} + {{\left( {z - {z_1}} \right)}^2}} } \end{array} $ | (5) |
线性化得:
| $ \begin{array}{*{20}{c}} {{d_{i, 1}}^2 + 2{d_{i, 1}}{d_1} = {d_i}^2 - {d_1}^2 = }\\ { - 2x{x_{i, 1}} - 2y{y_{i, 1}} - 2z{z_{i, 1}} + {D_i} - {D_1}} \end{array} $ | (6) |
式中,xi, 1=xi-x1;yi, 1=yi-y1;zi, 1=zi-z1;Di=xi2+yi2+zi2。初始位置P0(x0, y0, z0)的估计为:
| $ {P_0} = {\left( {\mathit{\boldsymbol{G}}_0^{\rm{T}}{\mathit{\boldsymbol{G}}_0}} \right)^{ - 1}}\mathit{\boldsymbol{G}}_0^{\rm{T}}{\mathit{\boldsymbol{H}}_0} $ | (7) |
其中,
| $ {\mathit{\boldsymbol{G}}_0} = - \left[ {\begin{array}{*{20}{c}} {\begin{array}{*{20}{c}} {{x_{2, 1}}}&{{y_{2, 1}}}\\ {{x_{3, 1}}}&{{y_{3, 1}}} \end{array}}&{\begin{array}{*{20}{c}} {{z_{2, 1}}}&{{d_{2, 1}}}\\ {{z_{3, 1}}}&{{d_{3, 1}}} \end{array}}\\ {\begin{array}{*{20}{c}} {{x_{4, 1}}}&{{y_{4, 1}}} \end{array}}&{\begin{array}{*{20}{c}} {{z_{4, 1}}}&{{d_{4, 1}}} \end{array}} \end{array}} \right] $ | (8) |
| $ {\mathit{\boldsymbol{H}}_0} = \frac{1}{2}\left[ {\begin{array}{*{20}{c}} {\begin{array}{*{20}{c}} {d_{^{2, 1}}^2 - {D_2} + {D_1}}\\ {d_{^{3, 1}}^2 - {D_3} + {D_1}} \end{array}}\\ {d_{^{4, 1}}^2 - {D_4} + {D_1}} \end{array}} \right] $ | (9) |
将式(3)在初始位置P0(x0, y0, z0)处进行泰勒级数展开,并忽略掉二阶以上分量,可得:
| $ \begin{array}{*{20}{c}} {{d_i} - {d_{0i}} = \frac{{{x_i} - {x_0}}}{{{d_{0i}}}}\left( {{X_{\rm{i}}} - {x_0}} \right) + }\\ {\frac{{{y_i} - {y_0}}}{{{d_{0i}}}}\left( {{Y_{\rm{i}}} - {y_0}} \right) + \frac{{{z_i} - {z_0}}}{{{d_{0i}}}}\left( {{Z_{\rm{i}}} - {z_0}} \right)} \end{array} $ | (10) |
式中,
一组观测时间内,运动目标在不同观测锚节点观测的移动标签位置不同。但由于UWB采样频率较高,认为一组较短的观测时间内,移动标签以速度v(vx, vy, vz)做匀速直线运动,则有:
| $\left\{ {\begin{array}{*{20}{c}} {{X_{\rm{i}}} = x + {v_x}\Delta {t_i}}\\ {{Y_{\rm{i}}} = y + {v_y}\Delta {t_i}}\\ {{Z_{\rm{i}}} = z + {v_z}\Delta {t_i}} \end{array}} \right.$ | (11) |
式中,Δti=ti-t1,ti为第i个观测锚节点与移动标签测距完成的时刻;p(x, y, z)为t1时刻对应的移动标签位置。将式(11)带入式(10)得:
| $ \begin{array}{*{20}{c}} {{d_i} - {d_{0i}} = \frac{{{x_i} - {x_0}}}{{{d_{0i}}}}\left( {x - {x_0}} \right) + \frac{{{y_i} - {y_0}}}{{{d_{0i}}}}\left( {y - {y_0}} \right) + }\\ {\frac{{{z_i} - {z_0}}}{{{d_{0i}}}}\left( {z - {z_0}} \right) + \frac{{{x_i} - {x_0}}}{{{d_{0i}}}}{v_x}\Delta {t_i} + \frac{{{y_i} - {y_0}}}{{{d_{0i}}}}{v_y}\Delta {t_i} + }\\ {\frac{{{z_i} - {z_0}}}{{{d_{0i}}}}{v_z}\Delta {t_i}} \end{array} $ | (12) |
记Δx=x-x0,Δy=y-y0,Δz=z-z0,写成矩阵形式为:
| $ \mathit{\boldsymbol{\varepsilon }} = \mathit{\boldsymbol{h\delta }} $ | (13) |
其中,
| $ \begin{array}{l} \mathit{\boldsymbol{\varepsilon }} = \left[ {\begin{array}{*{20}{c}} {\begin{array}{*{20}{c}} {{d_1} - {d_{01}}}\\ {{d_2} - {d_{02}}} \end{array}}\\ {\begin{array}{*{20}{c}} \vdots \\ {{d_N} - {d_N}} \end{array}} \end{array}} \right], \;\mathit{\boldsymbol{\delta }} = \left[ {\begin{array}{*{20}{c}} {\begin{array}{*{20}{c}} {\Delta x}\\ {\Delta y}\\ {\Delta z} \end{array}}\\ {\begin{array}{*{20}{c}} {{v_x}}\\ {{v_y}}\\ {{v_z}} \end{array}} \end{array}} \right], \;\\ \mathit{\boldsymbol{h}} = \left[ {\begin{array}{*{20}{c}} {\frac{{{x_1} - {x_0}}}{{{d_{01}}}}}&{\frac{{{y_1} - {y_0}}}{{{d_{01}}}}}&{\frac{{{z_1} - {z_0}}}{{{d_{01}}}}}&{\frac{{{x_1} - {x_0}}}{{{d_{01}}}}\Delta {t_1}}&{\frac{{{y_1} - {y_0}}}{{{d_{01}}}}\Delta {t_1}}&{\frac{{{z_1} - {z_0}}}{{{d_{01}}}}\Delta {t_1}}\\ {\frac{{{x_2} - {x_0}}}{{{d_{02}}}}}&{\frac{{{y_2} - {y_0}}}{{{d_{02}}}}}&{\frac{{{z_2} - {z_0}}}{{{d_{02}}}}}&{\frac{{{x_2} - {x_0}}}{{{d_{02}}}}\Delta {t_2}}&{\frac{{{y_2} - {y_0}}}{{{d_{02}}}}\Delta {t_2}}&{\frac{{{z_2} - {z_0}}}{{{d_{02}}}}\Delta {t_2}}\\ \vdots & & & & & \vdots \\ {\frac{{{x_N} - {x_0}}}{{{d_{0N}}}}}&{\frac{{{y_N} - {y_0}}}{{{d_{0N}}}}}&{\frac{{{z_N} - {z_0}}}{{{d_{0N}}}}}&{\frac{{{x_N} - {x_0}}}{{{d_{0N}}}}\Delta {t_N}}&{\frac{{{y_N} - {y_0}}}{{{d_{0N}}}}\Delta {t_N}}&{\frac{{{z_N} - {z_0}}}{{{d_{0N}}}}\Delta {t_N}} \end{array}} \right] \end{array} $ | (14) |
利用加权最小二乘算法,得到δ的最小二乘估计为:
| $ \mathit{\boldsymbol{\delta }} = {\left( {{\mathit{\boldsymbol{h}}^{\rm{T}}}{\mathit{\boldsymbol{Q}}^{ - 1}}\mathit{\boldsymbol{h}}} \right)^{ - 1}}{\mathit{\boldsymbol{h}}^T}{\mathit{\boldsymbol{Q}}^{ - 1}}\mathit{\boldsymbol{\varepsilon }} $ | (15) |
式中,Q是位置和速度的权值矩阵,选取合适的Q对最终的定位精度有着重要的影响,由于观测值的精度与距离有关,权值矩阵Q的选取可以根据对距离和速度的先验知识进行训练,以进一步提高定位精度。
算法初始迭代时,代入初始位置P0(x0, y0, z0)得到第一组(Δx, Δy, Δz)的值,在下一次迭代时,更新x0=x0+Δx,y0=y0+Δy,z0=z0+Δz,重复以上过程,当(Δx, Δy, Δz)足够小且其绝对值之和满足预先设定的阈值λ,即|Δx|+|Δy|+|Δz|≤λ时,另x=x0, y=y0, z=z0, 则p(x, y, z)即为经过多次迭代后估计得到t1时刻对应的移动标签位置。
3 位置精度因子精度因子可以从空间几何角度来描述系统环境分布的情况,其值越小,定位系统的空间分布越合理。位置精度因子(position dilution of precision,PDOP)可以用来衡量定位系统精度,PDOP值越小,定位精度越高[13]。作为选择空间中最优观测基站依据,其值可以通过观测数据的设计矩阵求得,令:
| $ \mathit{\boldsymbol{G}} = {\left( {{\mathit{\boldsymbol{A}}^{\rm{T}}}\mathit{\boldsymbol{A}}} \right)^{ - 1}} $ | (16) |
式中,A为关于目标位置分量的设计矩阵,根据式(12),可以写为:
| $ \mathit{\boldsymbol{A}} = \left[ {\begin{array}{*{20}{c}} {\frac{{{x_1} - {x_0}}}{{{d_{01}}}}}&{\frac{{{y_1} - {y_0}}}{{{d_{01}}}}}&{\frac{{{z_1} - {z_0}}}{{{d_{01}}}}}\\ {\frac{{{x_2} - {x_0}}}{{{d_{02}}}}}&{\frac{{{y_2} - {y_0}}}{{{d_{02}}}}}&{\frac{{{z_2} - {z_0}}}{{{d_{02}}}}}\\ \vdots &{}& \vdots \\ {\frac{{{x_N} - {x_0}}}{{{d_{0N}}}}}&{\frac{{{y_N} - {y_0}}}{{{d_{0N}}}}}&{\frac{{{z_N} - {z_0}}}{{{d_{0N}}}}} \end{array}} \right] $ | (17) |
代入式(16),G可表示为:
| $ \mathit{\boldsymbol{G}} = \left[ {\begin{array}{*{20}{c}} {{p_{11}}}&{{p_{12}}}&{{p_{13}}}\\ {{p_{21}}}&{{p_{22}}}&{{p_{23}}}\\ {{p_{31}}}&{{p_{32}}}&{{p_{33}}} \end{array}} \right] $ | (18) |
则PDOP值的计算公式为:
| $ {\rm{PDOP}} = \sqrt {{q_{11}} + {q_{22}} + {q_{33}}} $ | (19) |
实验采用的是基于DecaWave DWM1000测距开发板和STM32最小系统模块自主研发的UWB定位模块。在室内建立无遮挡测量环境,基站坐标为观测锚节点1(0, 0, 200)、观测锚节点2(0, 350, 200)、观测锚节点3(250, 350, 200)、观测锚节点4(250, 0, 200)、观测锚节点5(0, 350, 0)和观测锚节点6(250, 0, 0)。以50 cm为步长在地面上构建网格,网格交点如图 3所示。
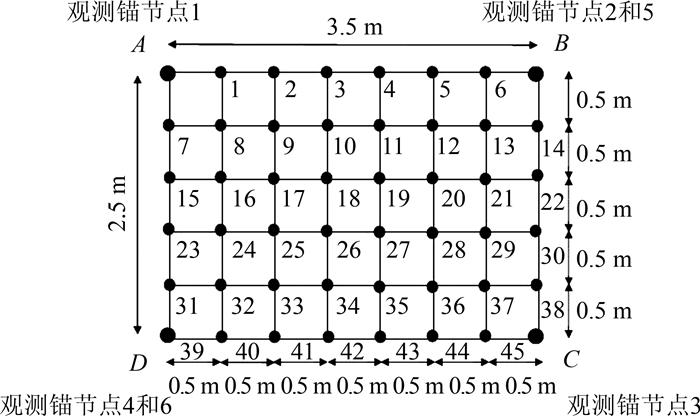 |
| 图 3 UWB定位模块分布 Fig.3 Modules Distribution of UWB Positioning |
4.2 实验环境PDOP分析
为了评定UWB定位系统布设环境的几何分布的合理性,实验选取环境中Z=100 cm这一平面,对其各个位置上的PDOP值进行计算,结果如图 4所示。
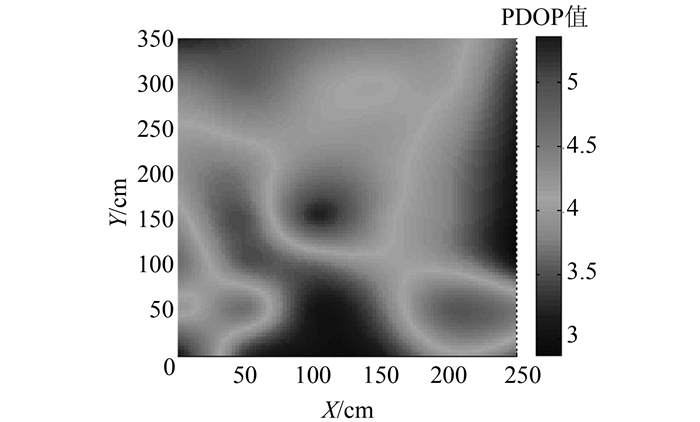 |
| 图 4 PDOP值 Fig.4 PDOP Value |
图 4中,PDOP最大值为5.35,最小值为2.94,能够满足高精度UWB室内定位需求。
4.3 静态定位结果及分析基于上述的UWB定位系统,为了分析本文算法在目标在静态条件下的定位精度,将静态目标放置于不同的网格点进行测距。根据长方形的对称原则,在保证能够获得足够多数据的前提下,将目标分别放置于点1(0, 50, 75)、点3(0, 150, 75)、点5(0, 250, 75)、点8(50, 50, 75)、点10(50, 150, 75)、点12(50, 250, 150)、点14(50, 350, 150)、点15(100, 0, 150)、点17(100, 100, 150)、点19(100, 200, 150)、点21(100, 300, 150)处。目标以轮询的方式在每个位置进行1000组测距,利用本文算法对每一组样本数据进行求解,并求出相应的平均值坐标和中位数坐标,并与实际位置进行比较,进而评估本文算法的定位精度和稳定性。结果如表 1所示。
| 表 1 不同网格点观测误差/cm Tab.1 Differences Observed at Grid Points/cm |
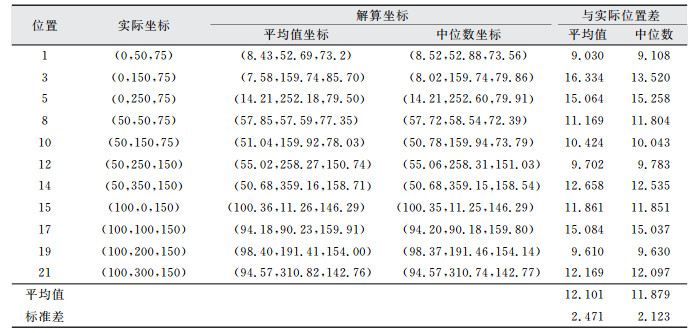 |
由表 1可以看出,对于三维环境中的静态目标,平均值坐标与实际坐标的误差平均值为12.101cm,标准差为2.471cm,中位数坐标与实际位置的定位误差为11.879 cm,标准差为2.123 cm。由此可见,定位结果的精度可达cm级,并且具有一定的稳定性,为进行动态定位提供了良好的实验基础。
4.4 动态定位结果及分析1) 单摆运动。选取Y-Z平面,使目标在平面内做单摆运动,分析在单摆运动过程中目标在Y轴和Z轴方向上坐标值的变化。图 5给出了单摆运动情况。可以看出,目标在Z轴和Y轴方向的变化呈正弦变化,能准确地体现单摆运动的规律。
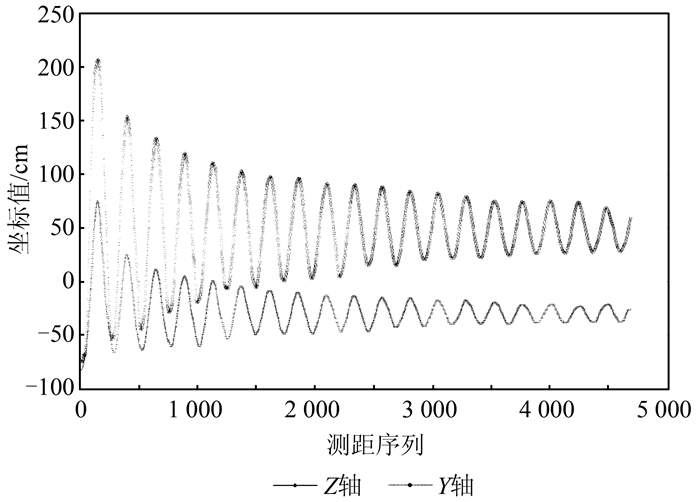 |
| 图 5 单摆运动 Fig.5 Simple Pendulum Motion |
2) 匀速直线运动。使目标从坐标(250, 0, 75)出发,沿DC直线运动至坐标(250, 350, 75)处,然后沿CB边移动到点(0, 350, 150), 最后沿BD连线返回起点(250, 0, 75),运动过程保持2 m/s的匀速直线运动。用Matlab根据求解的定位结果在真实轨迹附近的分布情况,分析动态定位的效果。首先,对运动路线上各个位置的PDOP值进行分析,如图 6所示。
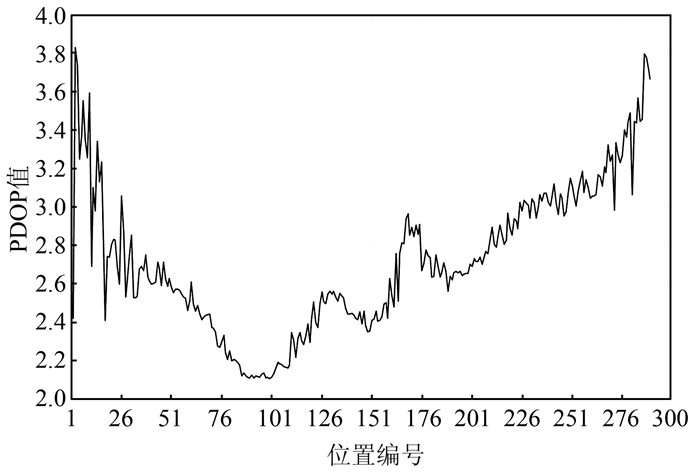 |
| 图 6 运动轨迹PDOP值变化 Fig.6 PDOP Change of Moving Trajectory |
从图 6中可以看出,动态验证实验的UWB定位系统的空间几何分布合理,可以满足高精度定位的要求。
图 7给出了运动轨迹点分布。图 7中,实线代表目标运动的真实轨迹;点代表解算求出的目标运动位置。可以看出,解算的轨迹点在真实轨迹附近的分布情况,解算得到的目标位置可以较好地反映目标运动的真实轨迹。
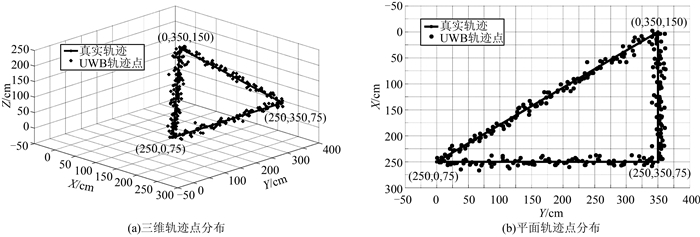 |
| 图 7 运动轨迹点分布 Fig.7 Trajectory Points Distribution |
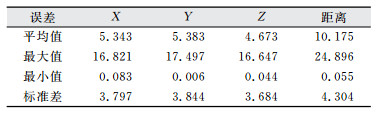
表 2给出了在X、Y、Z 3个分量以及距离上的定位误差。可以看出,测距的平均误差为10.175 cm,位置分量x、y、z的误差波动为4.5~18 cm,标准差在2~3.5 cm波动,说明顾及速度参数的解算模型可以精确、稳定地估计运动目标的位置。
| 表 2 动态定位误差分析/cm Tab.2 Error Analysis for Dynamic Positioning/cm |
 |
5 结束语
本文分析了基于DS-TWR的UWB室内定位模型,针对一组观测内运动目标位置变化的问题,提出了一种考虑速度参数的UWB定位解算方法。通过室内环境下对静态和运动目标的定位结果对比和分析,能够发现顾及速度参数的定位算法可以实现对运动目标的精确定位。然而,由于引入速度参数,本文算法需要的观测数也随之上升,从而提高基站布设成本,增加解算的时间花销,降低算法实时性。在今后的工作中,如何减少解算所需观测数量,进一步提高定位精度和实时性,分析不同运动情况下算法的表现,将成为今后深入研究的方向。
| [1] |
Zhang J, Orlik P V, Sahinoglu Z, et al. UWB Systems for Wireless Sensor Networks[J]. Proceedings of the IEEE, 2009, 97(2): 313-331. DOI:10.1109/JPROC.2008.2008786 |
| [2] |
许龙. 城市环境下基于降维Kalman滤波的室内导航算法[J]. 测绘地理信息, 2010, 35(4): 40-42. |
| [3] |
周建国, 张鹏, 冯欣, 等. 基于无线传感器网络的室内定位研究[J]. 测绘地理信息, 2012, 37(5): 26-28. |
| [4] |
汪洋, 张乃通, 唐珣, 等. UWB室内视距环境多径传播模型[J]. 通信学报, 2005, 26(10): 24-28. DOI:10.3321/j.issn:1000-436X.2005.10.006 |
| [5] |
蒋婷婷, 李畅怡, 郑国莘, 等. 基于UWB定位系统脉冲信号在多径信道传播的时延[J]. 微计算机信息, 2007, 23(27): 140-142. DOI:10.3969/j.issn.1008-0570.2007.27.055 |
| [6] |
Dardari D, Conti A, Ferner U, et al. Ranging with Ultrawide Bandwidth Signals in Multipath Environments[J]. Proceedings of the IEEE, 2009, 97(2): 404-426. DOI:10.1109/JPROC.2008.2008846 |
| [7] |
Farid Z, Nordin R, Ismail M. Recent Advances in Wireless Indoor Localization Techniques and System[J]. Journal of Computer Networks and Communications, 2013, 2013(42): 15. |
| [8] |
Schmitz J, Hernández M, Mathar R. Real-Time Indoor Localization with TDOA and Distributed Software Defined Radio: Demonstration Abstract[C]. The 15th International Conference on Information Processing in Sensor Networks, Vienna, Austria, 2016
|
| [9] |
Kolakowski M, Djaja-Josko V. TDOA-TWR Based Positioning Algorithm for UWB Localization System[C]. The 21st International Conference on Microwave, Radar and Wireless Communications (MIKON, 2016), Krakow, Poland, 2016
|
| [10] |
任斌, 徐会彬. 基于总体最小二乘的泰勒级数展开的TOA的UWB定位方法[J]. 科学技术与工程, 2013, 13(21): 6129-6133. DOI:10.3969/j.issn.1671-1815.2013.21.015 |
| [11] |
谢芝玉, 刘雄飞, 胡志坤. 基于Taylor展开的UWB井下定位算法研究与实现[J]. 计算机工程与应用, 2017, 53(2): 231-235. DOI:10.3778/j.issn.1002-8331.1504-0051 |
| [12] |
方姝, 倪育德, 刘逸, 等. 基于最小二乘与Taylor级数展开的新型混合定位方法[J]. 计算机工程, 2015(6): 316-321. DOI:10.3969/j.issn.1000-3428.2015.06.057 |
| [13] |
潘林, 蔡昌盛, 罗小敏, 等. 一种顾及权重的PDOP值计算方法[J]. 测绘科学技术学报, 2014(3): 236-239. DOI:10.3969/j.issn.1673-6338.2014.03.004 |
 2018, Vol. 43
2018, Vol. 43


