| 中国海域岛礁重力测量及潮汐改正 |
2. 武汉大学地球空间环境与大地测量教育部重点实验室,湖北 武汉,430079;
3. 地球空间信息技术协同创新中心,湖北 武汉,430079
2. Key Laboratory of Geospace Environment & Geodesy, Ministry of Education, Wuhan University, Wuhan 430079, China;
3. Collaborative Innovation Center of Geospatial Technology, Wuhan 430079, China
固体潮改正是重力测量改正的主要项,由固体潮改正引起的重力变化可达±300 μGal。在重力测量中,准确的固体潮改正应依据当地长时间固体潮观测获得的固体潮模型进行改正。由于不可能在每个测站都实现长期的固体潮观测,因此,固体潮改正通常是根据现有的理论固体潮改正模型计算出测站的固体潮改正值,从而对重力测量值进行改正。由于地球物性的非均匀性,采用理论固体潮模型代替测站模型会带来较大的误差,如岛礁重力测量。文献[1, 2]对北礵岛、平岛、小平岛以及海洋岛等4个岛礁绝对重力测量经过固体潮改正、海潮负荷改正、气压改正、极移改正、光速有限改正、仪器有效高度改正后组均值相对于总均值的差值(偏差)进行了分析。结果表明,即使在经过上述改正后,4个岛的偏差依然出现了较大的振幅,表明改正并不完全。其中平岛、小平岛和海洋岛呈近半日周期特征,北礵岛周期特征不明显;海洋岛的最大振幅超过了100 μGal,极大地影响了最终结果的准确度和精度。
潮汐因子的取值、改正方式的差异都可对潮汐改正精度造成影响[3, 4]。不同天文系统参数的选取以及模型的适用性也是固体潮改正时需要顾及的因素[5, 6]。固体潮改正依赖于固体潮模型。当地固体潮模型的获取通常有以下两种途径:①通过理论模型进行预测;②通过长时间的地面固体潮观测获得。Dehant等从理论上模拟了分层、旋转微椭球地球流体静力平衡和非流体静力平衡的固体潮潮汐参数[7]。Mathews采用由VLBI观测获得的液核共振周期对PREM模型的液核和地球的动力学扁率进行了修正,获得了另一个固体潮模型[8]。孙和平等利用国际地球潮汐中心收集到的全球地球动力学合作观测与研究网络超导重力仪总长806 673.36 h的观测资料,构建了基于液核共振效应的重力潮汐实测模型。该模型与Dehant等给出的DDW和Mathews给出的模型值最大差异为0.4%[9]。周江存等采用高精度引潮位展开表、重力固体潮理论模型[7, 8]和重力潮汐全球实验模型[9],远区采用NAO99全球海潮模型,近区采用文献[10]提供的中国近海潮汐资料,M4潮波采用FES04全球海潮模型值,构建了中国及邻区的精密重力潮汐改正模型,并提供了计算软件。通过与武汉站实测数据比较,周江存等的模型在中国大陆地区的重力潮汐改正模型精度优于0.5 μGal[11]。
要使重力潮汐改正的精度达到μGal级,则重力潮汐因子的精度应达到1%,相位延迟应达到0.50。《国家重力控制测量规范》(以下简称《规范》)采用了零潮汐改正,规定了高精度绝对重力测量的固体潮改正公式C.1[12],该公式依据的是1983年国际标准地球潮汐模型委员会提出的模型公式,由许厚泽进行了简化[13],通过求取日月的天文参数,从而在时间域内进行直接计算。《规范》中潮汐因子的取值或者计算式并没有明确给出。为了计算简便,在重力测量固体潮改正计算中,我国许多地区采用的潮汐因子值是1.16,该值是依据莫洛金斯基地球模型I计算得到的,我国内陆地区潮汐因子经海潮改正后接近这个值,适合精度要求较低的情形。Wahr在顾及地球自转及扁率的影响下,给出了一组潮汐因子计算公式,由于Wahr的潮汐因子理论值与实际潮汐观测结果有1%的系统偏低,为此,Melchior等给出了一组统计的潮汐因子计算公式[14],该公式与实测值相比较,在我国内陆相对偏差,优于或略大于1%,在北方和南方沿海地区大于1%。张宏伟对比了不同潮汐因子取值差异对我国重力测量的影响,建议对我国固体潮汐改正的潮汐因子取值进行划区处理[5]。
岛礁重力测量改正中,海潮负荷改正的量级仅次于固体潮改正,约为固体潮改正的15%。研究资料表明,对我国高精度重力测量进行海潮负荷改正是必要的[10, 15, 16]。从海潮负荷计算软件、地球模型和海潮模型中选取3个因素均能对海潮负荷改正的计算结果产生影响[17]。大气潮汐则更小,约为固体潮的1%。极移改正引起重力的长期变化,与测点的地理位置相关,其年变化小于10 μGal[16]。仪器高改正与测点重力垂直梯度有关,日变化是微小量。基于上述各项改正的量级分析,本文对目前的固体潮模型在我国岛礁重力测量的适用性进行了比较,对引起上述偏差的可能原因进行了分析。
1 模型适用性比较为了检验现有固体潮模型在我国岛礁重力测量固体潮改正的效果,在无法获得小平岛和海洋岛观测数据的情况下,利用平岛和北礵岛实测绝对重力测量数据,采用4种方式计算了两个岛在实测数据段的固体潮改正值以及最后的偏差。这4种方式分别代表了4种不同的固体潮改正模型,分别是《规范》中的公式C.1(简记为GFC1)、文献[10]中的潮汐改正计算软件(简记为JMCX)、TSOFT软件计算的固体潮改正值(简记为TSOFT)以及两岛观测采用的A10重力仪自带的g7软件(简记为g7)。其中在编制GFC1计算程序时,潮汐因子的计算采用了Melchior等的统计公式。TSOFT计算时采用的是1999微椭非弹性[7]、非流体静力平衡地球模型得到的固体潮模型。g7软件计算固体潮使用ETGTAB程序,利用Tamura分潮表。将GFC1、JMCX、TSOFT以及g7计算的固体潮值应用于平岛、北礵岛实测数据段的固体潮改正,计算组均值相对于总均值的偏差,4种模型的结果比较见图 1、图 2。由图 1、图 2可见,JMCX、g7、TSOFT的结果差异极小,在图中几乎完全重叠在一起,难以分辨。两个岛的误差统计见表 1。由于现行的《规范》中没有明确海潮负荷改正的处理,而海潮负荷计算软件、地球模型和海潮模型的选取并不能有效地消除上述偏差,因此,比较中海潮负荷改正都采用了g7软件提供的海潮负荷改正值。需要说明的是,平岛距离海岸约41 km,每30 min观测为一组,共记录98组。北礵岛距离海岸约25 km,每30 min观测为一组,共记录66组。在两岛均采用A10绝对重力仪施测,精度指标为10 μGal。两岛均同步进行了重力垂直梯度观测。
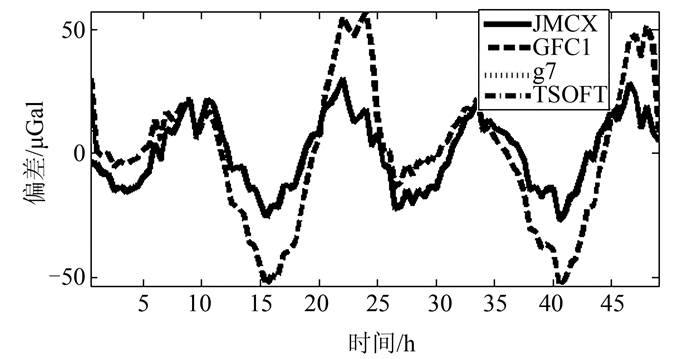 |
| 图 1 平岛偏差 Figure 1 Deviations of Pingdao |
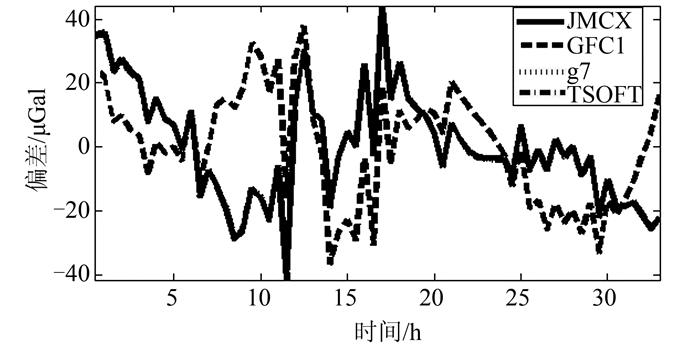 |
| 图 2 北礵岛偏差 Figure 2 Deviations of Beishuangdao |
| 表 1 平岛和北礵岛误差估计/μGal Table 1 Error Estimation of Pindao and Beishuangdao/μGal |
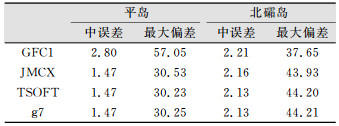 |
由图 1可知,在平岛应用GFC1、JMCX、TSOFT和g7等4个不同软件计算得到的固体潮值与观测值均出现了较大的偏差,且呈现近半日周期特性。其中GFC1最大振幅达57.05 μGal, JMCX最大为30.53 μGal,TSOFT最大为30.23 μGal,g7最大为30.25 μGal。由图 2可知,北礵岛偏差周期性不显著,GFC1最大振幅为37.65 μGal,JMCX最大为43.93 μGal,TSOFT最大为44.20 μGal,g7最大为44.21 μGal。两岛的偏差均已经超过了《规范》中对相对重力测量仪器标称精度的要求。由前述的各改正量级分析,即便顾及到A10绝对重力仪±10 μGal的精度,组均值相对于总均值的偏差产生如此大的振幅也说明改正不完全。此外,由表 1可见,JMCX、TSOFT及g7误差基本一致,而GFC1的误差较其他3个模型偏大。
由于无法获得小平岛和海洋岛的数据,并不能对这两个岛给出定量的结果。但由表 1可见,除了GFC1在应用到固体潮改正时精度比其他3个模型略差外,JMCX、TSOFT及g7模型在精度上并无明显差异。对于小平岛和海洋岛,纪立东等[2]采用的是ETGTAB计算固体潮,与本文中的g7一致,因此,笔者推测本文所采用的4种不同固体潮模型在应用于该两岛改正后,与纪立东等的结果相比,不会产生明显的差异,但依然会出现偏差较大的结果。当然,确切的结果需要进一步的定量计算。
平岛、小平岛和海洋岛均位于黄海,北礵岛位于东海。地质地球物理勘探目前均未在以上测区发现活动火山[18, 19],在施测期间也未发生强烈地震。因此,可以认为以上几个岛屿的重力测量结果没有受到活动岩浆和地震的影响。我国地域广阔,由于地球内部物质的不均匀性,固体潮模型的适用性在不同地区存在差异。以Dehant理论固体潮模型DDW为例,西北部的拉萨台站固体潮观测经过大气和海潮等改正后,与DDW模型存在很大差异。DDW理论模型S1波振幅因子与拉萨的观测结果差异达38.86%,O1、K1、M2和S2等4个主要潮波的平均差异超过1%。对文献[20]中潮波的差异取绝对值,绝对值平均差异为2.04%,去掉差异最大的S1波后,绝对值平均差异为0.99%。在中部的武汉站,观测固体潮参数在经大气、海潮等改正后则与DDW的结果符合较好,振幅因子日波平均偏差为0.59%,半日波偏差优于0.15%。在东南部的中国香港,孙和平等的计算显示,在不做近海验潮站数据改正的情况下,O1、K1、M2和S2经海潮负荷改正的固体潮重力潮汐参数与DDW理论地球潮汐模型的振幅因子差异优于1%。在考虑近海潮高变化效应后,相位滞后均得到了较好的改善,但O1和M2波振幅因子与DDW相比差异上升,O1波差异从0.98%上升为1.7%,M2波从0.55%上升为0.64%。同时,不同的海潮模型在中国香港对半日波段的负荷改正的有效性存在较大的差异[20-22]。可见,理论固体潮模型在我国不同地区的适用性存在差异。本文以平岛和北礵岛为例的模型适用性的比较也表明,即便在经过海潮负荷改正后,偏差也没有得到较好的改善。特别是海洋岛近100 μGal的振幅,难以用海潮模型精度较低来加以解释。因此,在进行岛礁重力固体潮改正时,固体潮模型的适用性是需要考虑的一个重要因素,而海潮模型的选取也是重力测量海潮负荷改正需要考虑的。
全球海潮模型的差异主要集中在浅水区域和极地地区,而全球海潮模型在中国海域的实用性也较差[23]。我国海域的潮汐性质比较复杂,但总体来说,渤海、黄海、东海的潮波以半日潮为主,尤其以M2、S2占主导优势。其中海洋岛和小平岛测区所在的辽东半岛从鸭绿江口沿辽宁海岸到大连老铁山为正规半日潮,由老铁山以北,经长兴岛、营口、葫芦岛至团山角为不正规半日潮。平岛所在的北黄海从靖海湾沿山东南岸到江苏海岸为正规半日潮。北礵岛所在的东海从宁波向南至厦门浮头湾以北都是正规半日潮[24-33]。平岛的偏差曲线与JMCX、TSOFT及g7计算的潮汐改正曲线相位具有较强的一致性,近半日周期特征明显,这也与该岛潮波以半日潮为主的认识相符,说明偏差产生的原因主要是由于潮汐改正不完全所致。至于固体潮模型的适用性差异与海潮模型的精度较差产生的偏差,哪一项是主要因素还需要更多的数据进一步研究。
北礵岛的偏差曲线在小潮期间的高潮和低潮时间出现了明显的震荡,偏差曲线相位与JMCX、TSOFT及g7计算的潮汐改正曲线不一致,偏差曲线出现了较大的滞后,但滞后与潮汐表预报高潮(低潮)相对于理论潮汐的滞后基本一致。北礵岛位于我国福建省三沙湾东北向,距离湾口的霞浦东冲验潮站约50 km,附近地形复杂,岛屿众多。三沙湾潮波为规则的半日潮,涨潮历时大于落潮历时,但是潮位日不等现象显著,在该岛重力施测时间段内,三沙湾当年小潮日不等达到最大,在东冲低潮日不等达到了120 cm[26],笔者推测这是北礵岛偏差曲线出现震荡的原因,也反映出该岛所处测区的海潮模型适用性较差。综上所述,笔者认为,造成两岛重力测量出现大幅偏差的原因是由于固体潮模型和海潮模型在施测区域的适用性较差引起的,至于两者中具体到某个岛礁上哪一项是主要的影响因素,还需要做进一步研究。
2 讨论《规范》对相对重力测量仪器的要求是标称精度为±20 μGal,绝对重力仪为±2 μGal。从图 1、图 2可见,岛礁重力测量由于潮汐模型误差引起的改正不完全而导致偏差的最大振幅已经大于《规范》所要求的精度要求。这意味着如果潮汐改正不完全,岛礁重力测量尤其是相对重力测量的结果存在普遍偏大或者偏小的可能,从而导致最终结果不准确。《规范》中要求相对重力测量测段应采用对称观测,即A-B-C…C-B-A,每条测线一般在24 h内闭合,特殊情况可以放宽到48 h。以平岛为例,在经过固体潮改正以及海潮改正后,平岛的偏差振幅峰值依然可达±30 μGal,峰值振幅差近60 μGal,且出现近半日的周期特征。如果按照24 h内闭合和A-B-C…C-B-A的对称观测要求,每个测站结果总体偏大或偏小并不能得到有效消除,并且误差也会带入到段差之中,即使增加仪器数量,也不能削弱该误差。
设测站A、B的观测值在经潮汐改正后的值分别为LA、LB,由于潮汐模型误差导致的改正误差分别为δgA、δgB,则真值分别为
1) 在进行海岛礁重力测量潮汐改正时,应谨慎选择固体潮模型。为了满足我国海域岛礁重力测量的高精度要求,应尽快建立适应于我国海域岛礁的高精度固体潮和海潮模型。
2) 在对岛礁实施重力测量前,应对岛礁所在海域的海洋潮汐特征进行调研,仔细制定观测时长和时间段。在缺少本地固体潮模型的情形下,岛礁相对重力测量应谨慎选择观测时间段,尽量选择在零潮汐附近进行观测。对于高精度的绝对重力测量,应在经济、效率允许的条件下尽量延长观测时间来提高最终的观测结果的精度,在组间隔0.5 h的要求下,最小观测时间不应少于24 h,观测时长最好采用12 h的整数倍。或者通过文献[1]的方法进行模型校准来提高改正精度。
3) 重力测量《规范》中,对于高精度重力测量,应该增加海潮负荷改正。
致谢: 感谢周江存博士提供JMCX软件。| [1] | 赵珞成, 罗志才, 许闯, 等. 岛礁重力测量潮汐改正新方法[J]. 武汉大学学报·信息科学版, 2015, 40(7): 913–916 |
| [2] | 纪立东, 张权, 张宏伟, 等. 潮汐对高精度重力测量的改正分析[J]. 测绘地理信息, 2014, 39(1): 26–28 |
| [3] | 许厚泽. 精密重力测量的潮汐改正[J]. 测绘学报, 1984, 13(2): 88–93 |
| [4] | 李金文. 不同固体潮改正公式及国家重力网的统一[J]. 武汉测绘科技大学学报, 1992, 17(3): 51–56 |
| [5] |
张宏伟. 海岛重力测量数据的预处理与分析[D]. 郑州: 信息工程大学, 2012 |
| [6] | 孙和平, DucarmeB, 许厚泽, 等. 基于全球超导重力仪观测研究海潮和固体潮模型的适定性[J]. 中国科学(D辑), 2005, 35(7): 649–657 |
| [7] | Dehant V, Defraigne P, Wahr J M. Tides for a Convective Earth[J]. J Geophys Res, 1999, 104(B1): 1 035–1 05 DOI: 10.1029/1998JB900051 |
| [8] | Mathews P M. Love Numbers and Gravimetric Factor for Diurnal Tides[J]. J Geodetic Soc Japan, 2001, 47(1): 231–236 |
| [9] | 孙和平, 徐建桥, DucarmeB. 基于全球超导重力仪观测资料考虑液核近半日共振效应的固体潮实验模型[J]. 科学通报, 2003, 48(6): 610–614 |
| [10] | 孙和平, 许厚泽, 周江存, 等. 武汉超导重力仪观测最新结果和海潮模型研究[J]. 地球物理学报, 2005, 48(2): 299–307 |
| [11] | 周江存, 徐建桥, 孙和平. 中国大陆精密重力潮汐改正模型[J]. 地球物理学报, 2009, 52(6): 1 474–1 482 |
| [12] |
中华人民共和国国家质量监督检验检疫总局. 国家重力控制测量规范: GB/T 20256-2006[S]. 北京: 中国标准出版社, 2006 |
| [13] | 许厚泽. 精密重力测量的潮汐改正[J]. 测绘学报, 1984, 13(2): 88–93 |
| [14] | Melchior P, Becker M D. A Discussion of World-Wide Measurements of Tidal Gravity with Respect to Oceanic Interactions, Lithosphere Heterogeneities, Earth's Flattening and Inertial Forces[J]. Physics of the Earth & Planetary Interiors, 1983, 31(1): 27–53 |
| [15] | 许厚泽, 孙和平, 徐建桥, 等. 武汉国际重力潮汐基准研究[J]. 中国科学(D辑), 2000, 30(5): 549–553 |
| [16] | 王勇, 张为民, 王虎彪, 等. 绝对重力测量的潮汐改正[J]. 大地测量与地球动力学, 2003, 23(2): 65–68 |
| [17] | 邓洪涛, 赵珞成. 海岛重力测量负荷改正及其影响因素分析[J]. 海洋测绘, 2017, 37(1): 14–16 |
| [18] | 高德章, 赵金海, 薄玉玲, 等. 东海重磁地震综合探测剖面研究[J]. 地球物理学报, 2004, 47(9): 853–861 |
| [19] | 郝天珧, 黄松, 徐亚, 等. 关于黄海深部构造的地球物理认识[J]. 地球物理学报, 2010, 53(6): 1 315–1 326 |
| [20] | 徐建桥, 陈晓东, 周江存, 等. 拉萨重力潮汐变化特征[J]. 科学通报, 2012, 57(22): 2 094–2 101 |
| [21] | 徐建桥, 周江存, 陈晓东, 等. 武汉台重力潮汐长期观测结果[J]. 地球物理学报, 2014, 57(10): 3 091–3 102 |
| [22] | 孙和平, 许厚泽, 陈武, 等. 香港地区重力固体潮和海潮负荷特征研究[J]. 地球物理学报, 2006, 49(3): 724–734 |
| [23] | 李大炜, 李建成, 金涛勇, 等. 利用验潮站资料评估全球海潮模型的精度[J]. 大地测量与地球动力学, 2012, 32(4): 106–110 |
| [24] |
吴俊彦, 肖京国, 成俊, 等. 中国沿海潮汐类型分布特点[C]. 中国测绘学会九届四次理事会暨学术年会, 桂林, 2008 |
| [25] | Fang Guohong. Tide and Tidal Current Chars for the Marginal Seas Adjacent to China[J]. Chinese Journal of Oceanology and Limnology, 1986, 4(1): 1–16 DOI: 10.1007/BF02850393 |
| [26] | 林航. 福建三沙湾的潮汐特征[J]. 福建水产, 2014, 36(4): 306–314 |
| [27] | 许闯, 吴云龙, 罗志才, 等. 基于短时间序列重力观测数据的潮汐改正方法[J]. 武汉大学学报·信息科学版, 2015, 40(2): 176–181 |
| [28] | 张贤林. 确定精密重力仪相位滞后方法的研究[J]. 地球物理学报, 1997, 40(3): 392–400 |
| [29] | 许厚泽. 固体地球潮汐[M]. 武汉: 湖北科学技术出版社, 2010 |
| [30] | 蒋骏, 张雁滨, 林钢, 等. 固体潮观测中的震颤异常波[J]. 地球物理学报, 2012, 55(2): 462–471 |
| [31] | 高茂生, 叶思源, 史贵军, 等. 潮汐作用下的滨海湿地浅层地下水动态变化[J]. 水文地质工程地质, 2010, 37(4): 24–27 |
| [32] | 杨锦玲, 关玉梅, 钟继茂, 等. 厦门重力固体潮海潮负荷改正研究[J]. 地球物理学进展, 2016, 31(3): 992–998 DOI: 10.6038/pg20160309 |
| [33] | 赵庆海, 郭玉良, 齐显峰. 大地测量数据处理中的潮汐系统和模型[J]. 海洋测绘, 2007, 27(6): 71–75 |
 2018, Vol. 43
2018, Vol. 43

