| BDS/GPS组合导航仿真实验研究 |
2. 成都大学建筑与土木工程学院,四川 成都,610106
2. School of Architecture and Civil Engineering, Chengdu University, Chengdu 610106, China
GPS是目前应用广泛的导航定位系统,它为全球用户提供高精度的导航定位服务,但是在观测条件较差、截止高度角较大情况下,可见卫星数和定位精度都大幅下降[1]。BDS是中国自主研发、独立运行的全球定位系统,目前处于建设研发阶段[2]。多星座组合定位导航的概念早在多年前已提出,对多系统组合导航的定位算法和精度的评定都进行了大量的研究[3]。吕金浩等[4]对组合系统单点定位、相对定位等算法原理进行了阐述,开发了相应软件并实现了组合定位功能。吴玲等[5]阐述了时空标准统一的前提下多星座导航定位解算,并验证了多星座导航系统在可见卫星数、定位稳定性和定位精度方面带来的提高。在多星座组合导航的研究中,国内外主要研究完整导航定位系统之间的组合。由于BDS的异构轨道星座的设计能够更好地覆盖GPS薄弱的高纬度地区,对异构轨道中,不同类型轨道在组合导航系统中作用与优劣势的研究还很少见。本文研究BDS及其不同组合方式下组合系统的导航精度,利用计算机程序模拟仿真星座数据,并计算其精度因子随时间的变化量,直观地展示目前BDS的建设成果以及组合系统对定位精度的提升情况[6]。
1 组合导航仿真的基本原理 1.1 时空基准的统一BDS与GPS是两个独立的导航定位系统[7],需要统一时空标准,北斗时(BeiDou time, BDT)和GPS时(global positioning system time, GPST)均采用原子时时间基准。GPST与BDT之间的转换关系为:
| $ {\rm{GPST}} = {\rm{BDT}} + 14 + {C_3} - {C_0} $ | (1) |
式中, C为GPST、BDT和国际时间局(Bureau International de I’ Heure,BIH)维持时间之间的偏差。
GPS使用WGS84坐标基准,BDS使用2000中国大地坐标系(China geodetic coordinate system 2000, CGCS2000)[8]坐标基准,两者处在cm级的误差水平,此处忽略此误差。
1.2 卫星位置计算卫星仿真目的是得到卫星在地固坐标系中的三维坐标。仿真计算时采用轨道坐标系和地固坐标系,根据卫星运动开普勒定理[9],可得到卫星在轨道坐标系中的坐标,通过卫星轨道坐标系到地固坐标系的数学转换模型可以得到卫星在地固坐标系中的三维坐标[10]。
通过地固坐标系与站心坐标系转换的数学模型[11],可得在用户位置下的站心直角坐标,算得站心极坐标,该极坐标可以用于卫星对于用户位置的可见性计算。设(X, Y, Z)为卫星站心坐标系下坐标,(R, A, E)为站心极坐标下坐标,卫星到测站距离R、卫星的方位角A和高度角E分别为:
| $ \left\{ \begin{array}{l} R = \sqrt {{X^2} + {Y^2} + {Z^2}} \\ A = \arctan (\frac{Y}{X})\\ E = \arctan (\frac{Z}{{\sqrt {{X^2} + {Y^2}} }}) \end{array} \right. $ | (2) |
本文通过未知数构成的权阵(PTP)-1计算位置精度因子(position dilution of precision,PDOP)值[12],权阵为:
| $ {({\mathit{\boldsymbol{P}}^{\rm{T}}}\mathit{\boldsymbol{P}})^{ - 1}} = \left[ {\begin{array}{*{20}{c}} {\sigma _x^2}&{{\sigma _{xy}}}&{{\sigma _{xz}}}&{{\sigma _{xt}}}\\ {{\sigma _{yx}}}&{\sigma _y^2}&{{\sigma _{yz}}}&{{\sigma _{ty}}}\\ {{\sigma _{zx}}}&{{\sigma _{zy}}}&{\sigma _z^2}&{{\sigma _{tz}}}\\ {{\sigma _{tx}}}&{{\sigma _{ty}}}&{{\sigma _{tz}}}&{\sigma _t^2} \end{array}} \right] $ | (3) |
式中, P表示几何矩阵,可得:
| $ {\rm{PDOP}} = \sqrt {\sigma _x^2 + \sigma _y^2 + \sigma _z^2} $ | (4) |
PDOP值的大小直观地反映卫星星座相对于用户的几何精度[13], 根据组合导航的基本原理设计程序实时计算对应用户位置下的PDOP值数据,以动态折线图的形式在仿真程序中展示,同时储存在TXT文本文件中以供后期的数据分析与处理。
2 BDS/GPS组合导航仿真设计本文仿真模拟GPS与BDS的多种组合方式[14],在单一系统卫星星座的仿真基础上,选取需要组合的相应轨道卫星,屏蔽非组合内的多余卫星。目的是为了验证异构轨道的BDS不同类型轨道在组合系统中的作用和对组合系统定位精度的影响。具体组合方式为:DBS独立系统[15]、GPS独立系统、BDS和GPS的组合、模拟BDS和GPS的组合、BDS的中地球轨道(medium earth orbit, MEO)和GPS的组合、BDS的MEO与BDS的倾斜地球同步轨道(inclined geosynchronous satellite orbit, IGSO)和GPS的组合。
仿真系统采用了Unity3D引擎进行可视化仿真,Unity3D是一款非常强大的可视化引擎,能轻松地制作逼真的三维可视化动画并完成各种复杂的交互任务。配合使用Visual Studio开发环境下C#语言编写仿真算法进行数据处理与计算[16]。本文针对多种组合导航方式设计的仿真系统工作流程图,如图 1所示。主要由以下4个部分组成:①读取星历数据, 本文采用真实精密卫星星历数据; ②处理卫星星历数据, 本文主要对卫星星历数据进行了由轨道坐标系到地固坐标系再到站心坐标系的转换; ③计算可见卫星数和精度因子PDOP值;④实现仿真模拟可视化显示。
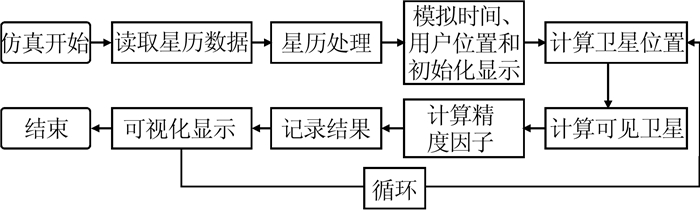 |
| 图 1 仿真系统的工作流程图 Fig.1 Flow Chart of Integrated Navigation System |
3 组合导航仿真实验与分析 3.1 仿真实验数据
仿真使用2013年7月3日的BDS和GPS的真实精密卫星星历为起算数据。仿真系统的起始时间模拟为2013年7月3日0时0分,模拟时间t的流逝速度为真实时间的3 600倍,仿真中1 s大约为真实的1 h,通过加快时间的流速以便通过动态仿真对卫星星座的运行和定位进行可视化。模拟用户位置采用成都、北京、上海、华盛顿、冰岛、基多、巴西利亚和堪培拉的大地经纬度数据。以上城市或国家的选取考虑到亚太地区、非亚太地区、中纬度、高纬度、低纬度的各种分布情况。
3.2 卫星可见数与分析通过图 2可知,对比华盛顿和巴西利亚的结果表明,仅能间断性地观测到BDS卫星,且数量极少,原因是BDS卫星并未覆盖到非亚太地区;在亚太地区的北京、上海、成都,BDS卫星可见数在8~13颗,GPS卫星数在7~11颗,组合系统卫星数在16~22颗,组合系统的卫星可见数明显增多,提高了GPS定位的稳定性;在太平洋边缘堪培拉卫星可见数BDS不及GPS,但组合系统卫星可见数大幅增加,GPS定位的稳定性有改善;在极地区域冰岛,观测到的BDS卫星数量仅少数时段能达到4颗,未能明显提高系统的定位稳定性,原因在于BDS建设尚未完成,已建成部分主要覆盖亚太地区,所以目前BDS还并未发挥出其异构轨道的设计优势。
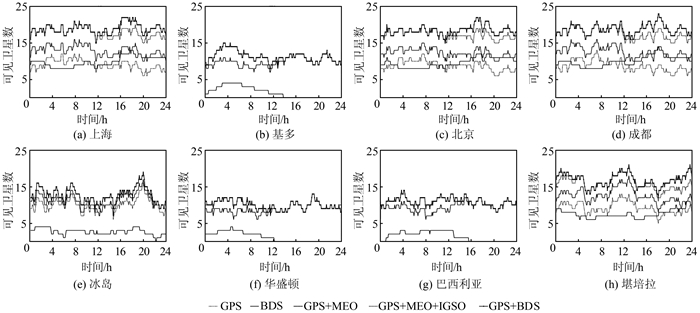 |
| 图 2 卫星可见数 Fig.2 Number of Visible Satellite |
3.3 PDOP值及结果分析
从整体上分析,由图 3看出,在非亚太地区华盛顿和巴西利亚,组合系统PDOP值并未改善;在亚太地区北京、上海、成都,组合系统PDOP值明显减小,且曲线更趋于平滑,表明组合系统对定位精度有很大提高,对比不同的纬度,BDS对GPS的改善程度随纬度增大而增大,BDS在高纬度区域较GPS更有优势;在亚太边缘地区,如太平洋中西部区域,BDS精度不及GPS,但在组合系统下,大大提高了GPS的定位精度。由于BDS目前只能覆盖亚太地区,所以在非亚太区域,BDS并未改善GPS的定位精度,本次实验对BDS系统建设的阶段性的性能有验证作用,对继续建设完善有参考价值,将来BDS系统建设完成后,在全球范围内的精度还有待进一步验证。从异构轨道的不同组合上分析,不同的组合方式下,精度和稳定性的提升主要来至卫星数量的增加。
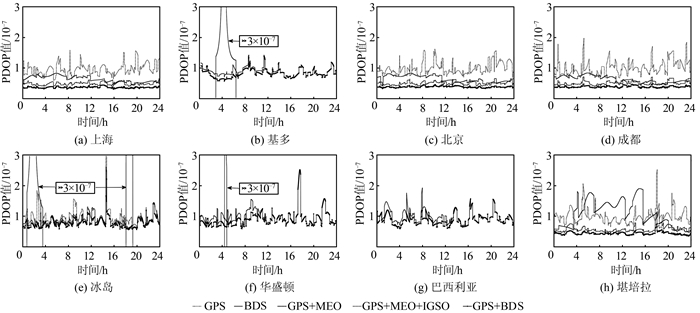 |
| 图 3 组合系统的PDOP值 Fig.3 Position Dilution of PDOP |
4 结束语
目前,组合导航仿真系统能明显地提高定位精度和稳定性,同时验证了现阶段中国BDS在亚太地区的优势, 以及在精度和稳定性方面的先进水平。本文设计的仿真程序算法精度会随着中国BDS的不断完善而提高,对于中国BDS的建设与研究具有参考意义。
| [1] |
李征航, 黄劲松. GPS测量与数据处理[M]. 武汉: 武汉大学出版, 2010.
|
| [2] |
郝金明, 刘伟平, 杨力, 等. 北斗卫星导航系统精密定轨技术研究现状[J]. 测绘科学技术学报, 2015, 32(3): 221-225. DOI:10.3969/j.issn.1673-6338.2015.03.001 |
| [3] |
曾庆化, 刘建业, 胡倩倩, 等. 北斗系统及GNSS多星座组合导航性能研究[J]. 全球定位系统, 2011, 36(1): 53-57. DOI:10.3969/j.issn.1008-9268.2011.01.011 |
| [4] |
吕金浩, 吕志伟, 杨剑伟, 等. GPS/BDS组合相对定位解算及精度分析[J]. 全球定位系统, 2014, 39(3): 4-7. |
| [5] |
吴玲, 孙永荣, 俞晓磊, 等. GPS/GLONASS/GALILEO多星座组合导航系统研究[J]. 中国空间科学技术, 2009, 29(3): 23-28. DOI:10.3321/j.issn:1000-758X.2009.03.004 |
| [6] |
张清华, 王源, 孙阳阳, 等. 北斗卫星导航系统空间信号可用性的初步评估[J]. 测绘地理信息, 2015, 40(6): 22-24. |
| [7] |
唐卫明, 徐坤, 金蕾, 等. 北斗/GPS组合伪距单点定位性能测试和分析[J]. 武汉大学学报·信息科学版, 2015, 40(4): 529-533. |
| [8] |
程鹏飞, 文汉江, 成英燕, 等. 2000国家大地坐标系椭球参数与GRS80和WGS84的比较[J]. 测绘学报, 2009, 38(3): 189-194. DOI:10.3321/j.issn:1001-1595.2009.03.001 |
| [9] |
刘基余. GPS卫星导航定位原理与方法[M]. 北京: 科学出版社, 2008.
|
| [10] |
崔立鲁, 何秀凤, 罗志才, 等. Galileo系统定位性能仿真模拟分析[J]. 测绘信息与工程, 2007, 32(4): 10-12. DOI:10.3969/j.issn.1007-3817.2007.04.005 |
| [11] |
李征航, 张小红. 卫星导航定位新技术及高精度数据处理方法[M]. 武汉: 武汉大学出版社, 2009.
|
| [12] |
王泽民, 孟泱, 伍岳, 等. GPS、Galileo及其组合系统导航定位的DOP值分析[J]. 武汉大学学报·信息科学版, 2006, 31(1): 9-11. |
| [13] |
刘季, 张小红. GPS/BD组合导航定位试验和精度分析[J]. 测绘信息与工程, 2012, 37(4): 1-3. |
| [14] |
高晓, 戴吾蛟. GPS-BD2组合相对定位精度分析[C].中国卫星导航学术年会, 武汉, 2013
|
| [15] |
杨鑫春, 李征航, 吴云. 北斗卫星导航系统的星座及XPL性能分析[J]. 测绘学报, 2011, 40(S1): 68-72. |
| [16] |
於宗俦, 鲁林成. 测量平差基础[M]. 北京: 测绘出版社, 1994.
|
 2019, Vol. 44
2019, Vol. 44

