| 一种三维数字城市自动纹理映射优化方法 |
2. 国家领土主权与海洋权益协同创新中心,湖北 武汉,430079;
3. 中冶建筑研究总院有限公司,北京,100088
2. Collaborative Innoation Center for Territorial Sovereignty and Maritime Rights, Wuhan 430079, China;
3. Central Research Institute of Building and Construction Co., Ltd., China Metallurgical Group Corporation, Beijing 100088, China
快速而高效地获取三维数字城市模型是三维重建的研究热点,而基于多视影像的快速自动三维建模技术是目前获得高保真模型的有效途径。该技术相比常规的利用3DSMax、Sketch Up[1]等三维建模设计软件,不仅效率提高,并且由于其自动化程度高,对从业技术人员要求也降低,为后续的基于三维数字城市的应用,如城市规划、抢险救灾、三维GIS等各行各业的应用减少了时间和经济成本。三维重建可分为几何重建和纹理重建两部分。几何重建已经取得了很好的效果,然而只有通过纹理映射,才能够建立具有真实感的模型。由于天气、光照等多种因素的影响,所获取的航空影像存在很大的色彩差异,导致最后的三维重建结果会存在很多的接缝。如何获得理想状态下的无缝纹理映射效果,很多学者进行了研究并提出了一些解决方法。刘彬等[2]提出一种多参数加权的无缝纹理映射算法,通过构造一个平滑的加权方程, 融合多源信息消除纹理的接缝。Lempitsky等[3]将纹理影像的选取视为三角网上多值标记问题,从而形成了一个标准马尔科夫随机场问题;然后,根据提出的一个接缝补平方法进行处理,弥补了边界处的接缝。Pan等[4]提出了一种色彩调整的方法来消除基于影像的三维纹理映射中的接缝现象。周漾[5]利用色彩变换的原理,采用以纹理三角形为处理基元,以三角网的边邻接关系为拓扑的面级别泊松融合。段春梅[6]提出基于马太效应的融合算法,通过一个迭代过程结合利用可见性和纹理区域构建的概率模型,将纹理碎片重新组合,从而来减少纹理接缝。由于是针对近景摄影测量等获取的小数据进行的实验,将该方法用于航空摄影测量的大数据时存在如纹理碎片过多等问题。Michael等[7]的方法计算量大,纹理接缝明显,依赖后期的色彩进行调整。综上所述,目前解决纹理接缝的主要方法有通过对纹理影像的选择进行优化和通过对纹理贴片间进行匀色两种。
本文在文献[6]的研究基础上针对航空影像的大数据结合马太效应和贪心算法实现了纹理映射优化。
1 纹理映射算法总体框架本文提出的纹理映射算法流程如图 1所示,输入参数为目标的三角网模型及对应的影像集和影像对应的内外方位元素。
 |
| 图 1 算法流程图 Fig.1 Flow Chart of Algorithm |
2 纹理分布优化算法
在基于多视图的纹理映射中,一个三角面可以同时被多张影像所见,三角面的纹理影像的选取决定了最终纹理映射的效果[8-10]。基于本文的纹理映射方案,将通过可见性分析后得到三角面的最优纹理影像分布,作为三角网模型的纹理影像初始分布。为了便于叙述,下面以单色图像代替影像来说明,不同颜色代表不同影像。
用t表示三角网模型中的任意三角面, N(t)代表其一邻域三角面集合,如图 2中黑色代表三角面t,灰色代表t的邻域三角面N(t),即具有共同顶点的三角面。C={Ci|i=1, …, N}表示输入纹理序列的颜色集合, N为颜色数, 即初始纹理影像数目。C(t)表示t的颜色, A(Ci)表示模型中属于颜色Ci的总的三角面个数, A(C(t))表示属于颜色C(t)的三角面的总个数。笔者把A(C(t))和A(Ci)简称为颜色面积。可见性系数集合V(t)扩展为V(t, Ci),表示t在Ci所代表图像中的可见性系数。同理,在三角面t的邻域N(t)中,NC={NCi|i=1, …, n}为表示邻域中纹理序列的颜色集合,n为颜色数即纹理影像的数目。C(t)表示t的颜色,Num表示三角面t的邻域三角面N(t)的总个数,NA(Ci)表示属于颜色NCi的三角面的个数。
 |
| 图 2 邻域三角面示意图 Fig.2 Neighborhood Triangles Diagram |
2.1 基于马太效应的纹理分布优化
在对模型的三角面选择纹理影像时,笔者优先考虑在模型上分布面积更多的纹理影像。故马太效应的思想与笔者所要解决的纹理映射中三角面纹理影像的选取原则不谋而合。
根据文献[6],本文依据马太效应原则提出了概率模型, 描述三角面t从颜色C(t)变为颜色Ci的概率为:
| $ {P_{t|C\left( t \right) \to {C_i}}} = {P_a} \times {P_v} $ | (1) |
式中,描述当前的颜色分布导致的积累优势效应的
同理,三角面t的颜色为C(t)的概率Pt为:
| $ \begin{array}{l} {P_t} = {\rm{ }}\frac{{A\left( {{C_t}} \right)}}{{A\left( {{C_1}} \right) + A\left( {{C_2}} \right) + \ldots + A\left( {{C_N}} \right){\rm{ }}}}{\rm{ }} \times {\rm{ }}\\ \;\frac{{V\left( {t, {C_t}} \right)}}{{V\left( {t, {C_1}} \right) + V\left( {t, {C_2}} \right) + \ldots + V(t, {C_n})}}{\rm{ }} \end{array} $ | (2) |
具体的纹理分布优化步骤。
1) 查找以最优纹理影像作为初始分布三角网模型中的所有边界三角形,认为相邻两个三角面的颜色不同,则参考纹理影像不同,即为边界三角形,并存储边界三角形。
2) 遍历边界三角形。统计出三角网模型中每个三角面t的对应颜色和整个三角网模型所使用到的纹理序列的颜色数N,并统计出每种颜色Ci所覆盖的模型三角形的个数A(Ci),对A(Ci)进行排序。
3) 根据反映马太效应运行核心趋势的平方根定律,认为在本文的算法中,对于N种颜色或输入纹理影像经过该纹理分布优化算法, 剩余大约
4) 当纹理重分布完成即当遍历完所有的边界三角形时停止。
2.2 基于贪心算法的纹理分布优化贪心算法的本质是在对问题求解时,总是作出在当前看来是最好的选择。也就是说,不从整体最优上加以考虑,所做出的仅是在某种意义上的局部最优解。基于马太效应从整体上对纹理分布进行了优化,但纹理接缝产生的根本原因是相邻三角面所选择的纹理影像不同。故本文再次结合三角面t的邻域三角面N(t)采用贪心算法进行处理。
基于贪心算法的纹理分布优化步骤。
1) 以马太效应的结果为基础,再次查找出边界三角形。
2) 遍历边界三角形,对每个边界三角形t查找其邻域N(t)的所有三角形,对邻域三角形的颜色数n进行统计并统计出每种颜色NCi对应的三角面个数NA(Ci),用公式NA(Ci)/Num计算出概率最大的颜色NCi且属于t的可见影像集的作为三角面t的新颜色,同时将邻域中的三角面的颜色与t的颜色不同的三角形加入边界三角形的序列。
3) 采用以上的贪心算法遍历,直到结束遍历,纹理分布不再改变时停止。此时即可得到最优的纹理分布。
3 实验与分析实验影像数据来源于某地区的倾斜航空影像,其中下视镜头的焦距为50.77 mm,前后左右的4个镜头焦距分别为82.27 mm、82.15 mm、82.04 mm、82.33 mm,影像的尺寸为8 176像素×6 132像素,像元大小为0.006 mm。实验的三角网模型数据顶点个数为260 709,三角面个数为519 255,输入影像数为44张。程序的运行环境为Windows 7、GTX960、16G、i7-4790 CPU@ 3.6GHz。实验结果利用Meshlab软件来进行显示。实验中分别利用单色影像来观察纹理的分布情况,如图 3所示,利用真实纹理影像来观察真实纹理贴图效果如图 4。图 5~图 7反映了局部纹理贴图效果。其中图 4、图 7所反映的文献[3]、文献[7]中所采用的基于马尔科夫随机场的方式所得到的纹理贴图效果,由于其构建能量函数时,平滑项表示被贴上不同标签的两个相邻三角面的公共边投影到两张对应影像上的像素值差异性积分。故使用单色影像时无法体现影像的特征和影像间的色彩差异程度,无法正常计算。此处仅利用真实影像的贴图效果与本文算法结果进行对比。同时,也将本文算法结果与商业软件ContextCapture结果进行了对比。
 |
| 图 3 单色影像贴图效果图 Fig.3 Solid Color Image Texture Renderings |
 |
| 图 4 真实影像贴图效果图 Fig.4 Real Image Texture Renderings |
 |
| 图 5 局部贴图效果对比图 (与马太效应对比) Fig.5 Local Texture Comparison (To Mattew Effect) |
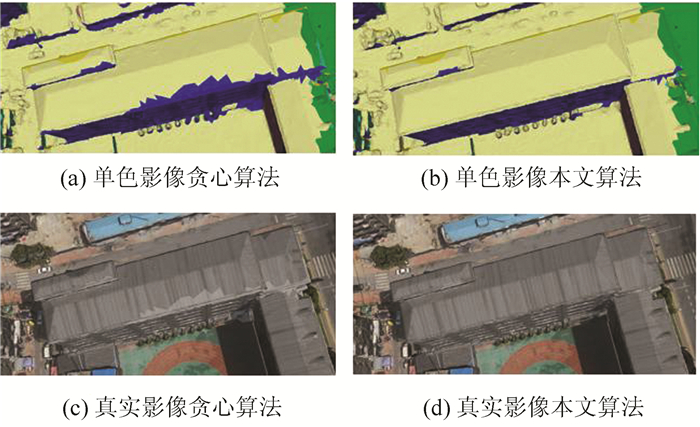 |
| 图 6 局部贴图效果对比图 (与贪心算法对比) Fig.6 Local Texture Comparison (To Greedy Algorithm) |
 |
| 图 7 局部贴图效果对比图 (与基于马尔科夫随机场对比) Fig.7 Local Texture Comparison (To Markov Random Field) |
表 1分别对马太效应、贪心算法、马尔科夫随机场以及本文的算法在纹理影像数目、纹理分布优化后得到的纹理块个数以及算法时间进行了统计。
| 表 1 算法效果统计表 Tab.1 Algorithm Effect |
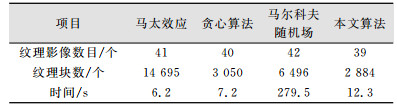 |
从表 1中可以看出,由于本文针对的是航空摄影测量的三维数字城市模型数据,地面的起伏比较大,模型覆盖区域面积广,故纹理影像数目上并没有太大的改变。从纹理块个数上来看,本文算法相比单独的马太效应有较大改善。由图 5也可看出,单独基于马太效应的纹理优化分布由于过多地考虑三角形纹理影像在整体中的分布概率,忽视了邻域关系,导致很多的纹理碎片,故纹理块个数多于另外几种方法。从纹理块个数上看,本文方法相比单独的贪心算法虽改善不大,然而由图 6可看出,单独基于贪心算法的纹理分布算法,由于只考虑了邻域三角形的影响,仅仅达到了局部最优的纹理分布,不能得到整体最优的结果,所以尽管从纹理块个数上看和本文算法类似,但从效果上看,本文的算法更好。最后,从时间效率上来看,本文方法的时间消耗相比马太效应和贪心算法稍多一点,但这几种方式相比基于马尔科夫随机场,时间消耗非常少。由表 1和图 7可见,本文算法在时间和效果上都要优于马尔科夫随机场的结果,并且效果上接近于商业软件ContextCapture的贴图效果。综上所述,本文方法结合了马太效应和贪心算法的优点,得到了一个整体最优的分布。
4 结束语本文提出的纹理分布优化方法在一定程度上减少了纹理接缝,明显提高了三维数字城市重建结果,算法原理简单且时间消耗少,具有一定的实际意义。由于影像间始终存在着不可避免的色彩及亮度差异。所以在进行完纹理分布优化后,为达到更好的无缝映射效果,后续还应该进行纹理间匀色的工作[9, 10],这能改善后面的贴图效果,对贴图后再次进行匀色也十分有必要,未来会继续针对贴图后纹理块间匀色这方面进行研究和完善。
| [1] |
万宝林. 3DS Max与Sketch Up的三维城市建模技术实验对比分析[J]. 测绘地理信息, 2015, 40(2): 23-25. |
| [2] |
刘彬, 陈向宁, 薛俊诗. 多参数加权的无缝纹理映射算法[J]. 中国图像图形学报, 2015, 20(7): 929-936. |
| [3] |
Lempitsky V, Ivanov D. Seamless Mosaicing of Image-Based Texture Maps[C]. 2007 IEEE Conference on Computer Vision and Pattern Recognition, Piscata-way, 2007
|
| [4] |
Pan R, Taubin G. Color Adjustment in Image-Based Texture Maps[J]. Graphical Models, 2015, 79: 39-48. DOI:10.1016/j.gmod.2015.04.002 |
| [5] |
周漾.馆藏文物纹理重建与组织关键技术研究[D].武汉: 武汉大学, 2013
|
| [6] |
段春梅.基于多视图的三维模型重建方法研究[D].济南: 山东大学, 2009
|
| [7] |
Michael W, Nils M, Michael G. Let There Be Color! Large-Scale Texturing of 3D Reconstructions[M]. Cham, Switzerland: Springer International Publishing, 2014.
|
| [8] |
张剑清, 贺少军, 苏国中. 三维模型重建中影像纹理重组织方法研究[J]. 武汉大学学报·信息科学版, 2005, 30(2): 115-117. |
| [9] |
王邦松, 艾海滨, 安宏, 等. 航空影像色彩一致性处理算法研究[J]. 遥感信息, 2011(1): 45-49. DOI:10.3969/j.issn.1000-3177.2011.01.009 |
| [10] |
詹总谦, 饶友琢. 秩亏自由网平差在近景影像色彩均衡处理中的运用[J]. 遥感信息, 2014, 29(6): 3-5. DOI:10.3969/j.issn.1000-3177.2014.06.001 |
 2019, Vol. 44
2019, Vol. 44

