| 遥感GPP模型在亚热带常绿林的应用比较 |
2. 中国科学院成都山地灾害与环境研究所,四川 成都,610041;
3. 中国科学院大学,北京,100049
2. Institute of Mountain Hazards and Environment, Chinese Academy of Sciences, Chengdu 610041, China;
3. University of Chinese Academy of Sciences, Beijing 100049, China
陆地生态系统总初级生产力(gross primary productivity,GPP)作为一个估算地球支持能力和评价生态系统可持续发展的重要指标[1],对其进行定量评估对深入了解陆地生态碳循环的过程及调控机制,客观评价生态系统的碳源/汇属性,预测未来气候变化意义重大。
涡度相关通量(eddy covariance)方法是一种直接观测生态系统和大气间CO2和水热通量交换的标准方法,不仅可以对净生态系统生产力(net ecosystem productivity,NEP)直接观测,也为生态系统GPP的估算提供了一种可行的方法(GPP=NEP+Re, Re为生态系统呼吸(ecosystem respiration))[2]。但是由于其提供点尺度上的各项生态系统碳通量观测数据为离散分布的空间点,空间连续性较差,难以用在区域尺度和全球尺度的碳通量空间格局的描述和研究中。因此具备区域甚至全球的观测覆盖能力, 能够提供时空连续的植被变化信息,并把通量塔观测数据和遥感数据相结合而发展起来的陆地生态系统生产力估算模型的卫星遥感,可以弥补在大面积区域缺乏广泛通量塔观测的缺陷[3]。近年来,相关学者提出了很多基于遥感的GPP估算模型,如VPM模型[4]、EC-LUE模型[5]、MODIS-PSN模型[6]以及TG模型[7]等,以适应区域甚至全球尺度生态系统生产力监测与评估的需求。
目前,我国有关森林生态系统固碳动态的研究多在温带或暖温带进行,对亚热带区的研究工作正在快速发展中,但仍较为欠缺。常绿阔叶林(evergreen broad-leaf forest,EBF)和常绿针叶林(everygreen needleleaved forset, ENF)作为亚热带典型的植被类型,探讨遥感模型在两种植被类型的应用具有重要意义。本文基于卫星遥感资料以及地面气象观测资料,利用3个总初级生产力(GPP)遥感估算模型估算了2003~2005年基于站点水平的亚热带常绿林生态系统总初级生产力(GPP),对比分析了不同模型的估算能力。
1 数据来源及模型介绍 1.1 数据来源及预处理千烟洲通量观测站(115°01′13″E, 26°44′48″N)位于江西省泰和县中国生态系统研究网络千烟洲试验区西南部。实验站现有植被大多是1985年前后人工种植的针叶林,通量塔周围近100 km2范围内森林覆盖率达70%[8]。千烟洲4~9月为生长季,10月到次年3月为非生长季。鼎湖山通量观测站(112°32′10″E, 23°10′24″N)位于广东省肇庆市鼎湖山保护区内。鼎湖山地区由于其独特的地理位置、气候条件和人文因素,仍然保存有比较完整的、典型的南亚热带地带性植被常绿阔叶林,成为当今地球该纬度带上最具特色和研究价值的地区之一[9]。
国际通量观测研究网络的建立,为区域或全球尺度的碳水循环模拟提供了强有力的数据基础。本文使用中国通量观测研究联盟网站(http://www.chinaflux.org/)提供的千烟洲(QYZ)以及鼎湖山(DHS)2003~2005的涡度相关通量观测数据。具体数据项包括辐射数据、气象数据(温度和降水)和通量观测数据(生态系统净交换(net ecosystem exchange, NEE)和生态系统呼吸,总初级生产力GPP通过公式GPP=Re-NEE得到。为了与各GPP模型模拟步长匹配,GPP与光合有效辐射(photosynthetic active radiation, PAR)采用8 d的累加值,气温采用8 d的平均值。数据在使用前进行了处理,如坐标轴旋转、WPL校正、无效数据剔除以及夜间通量摩擦风速订正等。
同时,下载了2003~2005年间两个站点周边的地表反射率产品MOD09A1和地表温度产品MOD11A2以及MOD17A2数据产品(https://ladsweb.nascom.nasa.gov/)。其中MOD17A2是基于光能利用率的GPP产品。根据站点通量塔的经纬度信息,提取和处理了千烟洲(QYZ)和鼎湖山(DHS)观测站附近3 km×3 km范围内的反射率、地表温度以及GPP数据。应用反射率数据的蓝波段(459~479 nm),红波段(620~670 nm),近红外波段(841~875 nm)和短波红外波段(1 628~1 652 nm)4个波段的反射率进行植被指数的计算。本文用到的植被指数包括增强植被指数(enhanced vegetation index, EVI)[10]、归一化植被指数(normalized difference vegetation index, NDVI)和陆地水分指数(land surface water index, LSWI)[11-15]。为了消除云、气溶胶、传感器等因素对EVI、NDVI和LSWI数据的影响,采用TIMESAT软件对植被指数数据进行平滑处理,剔除异常值。
1.2 GPP估算模型介绍 1.2.1 VPM模型VPM(vegetation photosynthesis model)模型是以涡度通量观测资料为基础,以遥感数据为驱动变量,模拟生态系统总初级生产力的光能利用率模型。VPM被广泛应用在不同区域生态系统GPP估算过程中,模型采用LUE模型的一般形式:
| $ {\rm{GPP}} = {\varepsilon _g} \times {\rm{FPA}}{{\rm{R}}_{{\rm{PAV}}}}{\rm{ \times PAR}} $ | (1) |
式中,εg为光能利用效率受气温、水分和叶物候影响的变量;FAPARPAV为植被冠层吸收光合有效辐射的比率;PAR为光合有效辐射。
VPM模型中光能利用率(εg)表示为最大光能利用率(ε0)和温度胁迫系数(Tscalar)、水分胁迫系数(Wscalar)的函数,计算公式如下:
| $ {\varepsilon _g} = {\varepsilon _0} \times {T_{{\rm{scalar}}}} \times {W_{{\rm{scalar}}}} \times {P_{{\rm{scalar}}}} $ | (2) |
| $ {T_{{\rm{scalar}}}} = \frac{{(T - {T_{\min }})(T - {T_{\max }})}}{{[(T - {T_{\min }})(T - {T_{\max }})] - {{(T - {T_{{\rm{opt}}}})}^2}}} $ | (3) |
| $ {W_{{\rm{scalar}}}}{\rm{ = }}\frac{{{\rm{1 + LSWI}}}}{{{\rm{1 + LSW}}{{\rm{I}}_{{\rm{max}}}}}} $ | (4) |
| $ {\rm{FAPA}}{{\rm{R}}_{{\rm{PAV}}}} = a{\rm{ \times EVI}} $ | (5) |
式中,T为气温(℃);Tmin为光合最低温度(℃);Tmax为光合最高温度(℃);Topt为光合最适温度(℃);当T小于Tmin时,Tscalar等于0。LSWI为陆地表面水分指数;LSWImax为生长季最大陆地表面水分指数。
1.2.2 EC-LUEEC_LUE(eddy covariance-light use Efficiency model)模型是基于涡度相关碳通量站点资料发展起来的光能利用率模型。采用蒸发系数(evaporative fraction,EF)作为湿度对最大光能利用率的调节作用,将EF(f(w))引入模型中在一定程度上使碳通量和水通量藕合在一起,从而解决了土壤含水量等因子难以获取的弊端,提高了模型的精确性和尺度上推可行性[15]。EC-LUE模型的输人变量主要包括归一化植被指数(NDVI)、光合有效辐射(PAR)、温度以及波文比(f(w))。
| $ {\rm{GPP = }}{\varepsilon _{\rm{0}}}{\rm{ \times min}}(f(T{\rm{), }}f(W{\rm{)) \times }}f{\rm{PAR \times PAR}} $ | (6) |
| $ f{\rm{PAR}} = 1.24 \times {\rm{NDVI - 0}}{\rm{.168}} $ | (7) |
| $ f{\rm{(W) = }}\frac{{{\rm{LE}}}}{{{\rm{HS + LE}}}} $ | (8) |
式中,PAR是光合有效辐射;LE是潜热;HS是显热。
1.2.3 TG模型TG(temperature and greenness model)模型是基于遥感的GPP估算模型,不需要地面观测数据作为模型输入,是一个完全基于遥感数据的GPP模型。
| $ {\rm{GPP = }}m \times \left( {{\rm{EV}}{{\rm{I}}_{{\rm{Scaled}}}} \times {\rm{LS}}{{\rm{T}}_{{\rm{Scaled}}}}} \right) $ | (9) |
| $ {\rm{EV}}{{\rm{I}}_{{\rm{Scaled}}}}{\rm{ = EVI - 0}}{\rm{.1}} $ | (10) |
| $ {\rm{LS}}{{\rm{T}}_{{\rm{Scaled}}}}{\rm{ = }}\min \left[ {\left( {{\rm{LST/30}}} \right);\left( {2.5 - \left( {0.05{\rm{LST}}} \right)} \right)} \right] $ | (11) |
式中,参数m通过模型标定得到;LST(Land surface temperature)是地表温度。
2 数据分析与结果 2.1 模型标定与验证对于VPM和EC-LUE模型,其输入参数如最大光能利用率采用经验值,植被指数、温度等数据则可以通过遥感数据和地面观测数据得到,因此这两个模型可以不进行模型标定。但是模型标定对TG模型估算精度有很大影响,同时为了获取TG模型输入参数m, 本文将所有数据随机分为两部分,数据的70%用于模型标定,余下30%的数据用于模型验证分析。模型标定与验证结果(表 1)表明,TG模型在标定阶段估算误差较大,但在模型验证阶段各模型精度都有一定程度的提高。8 d的标定后TG模型参数值m:千烟洲为151.24 g·C·m-2;鼎湖山为97.26 g·C·m-2。
| 表 1 TG模型标定与验证 Tab.1 Calibration and Validation for TG Model |
 |
2.2 模拟GPP与涡动相关估算GPP的对比
表 2对各种GPP模型在研究期内(8 d)的估算精度按站点(千烟洲以及鼎湖山)分别进行了统计分析。总体来说,这些预测模型模拟效果都不好,但所有模型(VPM、EC-LUE、TG)都要优于MOD17(R2分别为0.50,0.32)的模拟效果。表 2中,在千烟洲生态站,上述所有估算模型都低估了实测GPP,除了EC-LUE模型,其他各模型的偏差几乎都大于15 g·C·m2·8-1。尽管VPM、EC-LUE和TG的R2值差不多都为0.79,但EC-LUE模型的RMSE以及偏差都要最小。这说明在亚热带常绿针叶林的GPP估算中,EC-LUE模型具有较好的模拟效果。对于鼎湖山生态站,预测模型模拟效果较差(R2都小于0.70),除了EC-LUE模型,其他模型都低估了实测GPP。所有模型中,VPM模型具有最高的R2以及较小的偏差,而EC-LUE模型R2仅为0.48,说明水汽压是影响EBF生态系统光能利用率大小的重要环境因子。EC-LUE模型在ENF生态系统中低估量最小并且在EBF生态系统中高估了实测GPP,是因为fPAR是基于植被冠层叶绿素水平的,所以会在一定程度上高估GPP。
| 表 2 通量观测数据与模型模拟结果的比较 Tab.2 Performance of Models over the Study Period |
 |
2.3 模拟GPP与实测GPP季节动态上的差异
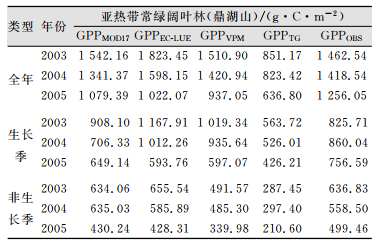
对模拟GPP与实测GPP在全年以及生长季(6个月)、非生长季(6个月)尺度上进行了对比(表 3、表 4)。对亚热带针叶林(千烟洲)来说,GPPMOD17、GPPEC-LUE、GPPVPM和GPPTG全年分别低估了41.27%、17.97%、39.88%、38.48%;生长季分别低估37.83%、4.81%、29.35%、29.06%;而非生长季则分别低估了49.07%、48.03%、63.97%、60.17%。对亚热带阔叶林(鼎湖山)来说,GPPMOD17、GPPVPM、GPPTG全年分别低估了4.69%、7.31%、44.35%,而GPPEC-LUE高估了6.24%;对于生长季GPPMOD17和GPPTG分别低估7.36%、38.08%,而GPPEC-LUE、GPPVPM分别高估了12.54%、3.72%;非生长季则分别低估了0.2%、2.13%、22.62%、53.15%。说明EC-LUE模型在亚热带常绿针叶林的全年尺度和生长季尺度上的模拟效果最好,而VPM和MOD17模型适合于亚热带阔叶林的GPP估算。
| 表 3 亚热带常绿针叶林(千烟洲)年度和季节尺度(4~9月,10~3月)GPP遥感模型和涡度协方差通量塔观测GPP的统计 Tab.3 The Annual and Seasonal Scale (from April to September, from October to March) Camparison Between GPP Model and Eddy Convariance in Subtropical ENF (Qianyanzhou) |
 |
| 表 4 亚热带常绿阔叶林(鼎湖山)年度和季节尺度(4~9月,10~3月)GPP遥感模型和涡度协方差通量塔观测GPP的统计 Tab.4 Annual and Seasonal Scale (from April to September, from October to March)Camparison Between GPP Model and Eddy Convariance in Subtropical EBF (Dinghushan) |
 |
2.4 GPP与模型输入因子的关系
在GPP估算中VPM、EC-LUE和TG模型估算精度都要比MOD17高,不同模型在两个站点的生态系统中预测结果也有一定的差异。拟分析实测碳通量数据与主要输入参数之间的依赖性,进一步探讨各模型在亚热带常绿针叶林与常绿阔叶林生态系统中的适用性。
EVI和PAR作为所有模型的输入参数,是影响GPP模拟精度的重要因子。由表 5可知,EVI与千烟洲观测站实测GPP的判定系数为0.72,大于EVI与鼎湖山观测站实测GPP的判定系数,仅为0.48。可见,在亚热带常绿针叶林(ENF)的GPP估算中,EVI和实测GPP之间的相关性较大,在亚热带常绿阔叶林(鼎湖山)的GPP估算中其相关性较小。因此需要考虑更多其他的环境参数。同时,在千烟洲观测站PAR和实测GPP的判断系数为0.64,在鼎山湖观测站为0.72,两个观测站的PAR和实测GPP判断系数较为接近,并且都大于0.5。在千烟洲观测站NDVI和LSWI与实测GPP的判定系数都要大于在鼎湖山的判定系数值。说明ENF观测地区的植被指数和陆地水分指对GPP的值均有较强的影响。
| 表 5 不同环境参数之间的相关性 Tab.5 Correlation Coefficient Values Between Various Factors |
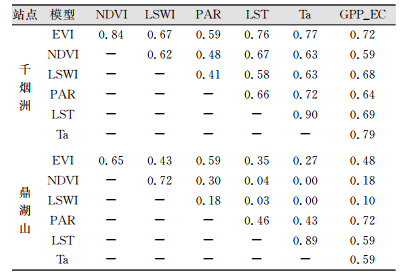 |
分析表 5可得,千烟洲实测GPP与各环境参数的相关性和鼎湖山实测GPP与各环境参数的相关性差异较大。千烟洲观测站的实测GPP与各个环境参数的判断系数均大于0.5,相关性比较大。并且实测GPP与各环境参数的判断系数差异小,最高为空气温度(temperature air, Ta):0.79,最低为NDVI为0.59,相差仅0.2。鼎湖山观测站的实测GPP与各个环境参数的判断系数之间的差异较大,与PAR判断系数最大,为0.72,与LSWI判断系数最小为0.1,相差0.62。其相同点在于,其相关系数最大的3个均有LST和Ta,这说明温度在ENF和EBF的GPP估算中都起到重要的作用。
3 结束语本文结合涡动相关法和光能利用率模型获得了千烟洲和鼎湖山的2003~2005年的GPP,分别代表了亚热带常绿针叶林(ENF)和亚热带常绿阔叶林(EBF)两种不同植被覆盖类型的GPP,对4种不同的光能利用率模型(MOD17、VPM、EC-LUE、TG)的在ENF和EBF中的模拟精度进行了评价。
1) 在标定阶段,TG模型低估了实测GPP,在千烟洲观测站TG判断系数为0.79;在鼎湖山观测站判断系数为0.65。
2) 在8 d的GPP模拟中,MOD17的模拟效果最差,其判断系数在千烟洲观测站为0.5,在鼎湖山观测站只有0.32,而其他模型(EC-LUE除外,其判断系数在鼎湖山观测站为0.48)判断系数都很高,均大于0.6;其次,相同的模型在不同的生态系统中模拟效果不同,EC-LUE在亚热带常绿针叶林(千烟洲)的判断系数为0.79,在亚热带常绿阔叶林(鼎湖山)只有0.48。
3) 在模拟GPP与涡动相关估算GPP的对比中,无论是ENF还是EBF中,EVI模型的模拟效果都是最差的;在千烟洲站点,MOD17模型全年尺度上低估了41.27%,生长季低估了37.83%,非生长季EC-LUE模型效果最差,低估了63.97%;在鼎湖山站点,TG模型在全年尺度上低估49.50%,生长季低估了38.08%,非生长季低估了53.15%;由此可见,无论是亚热带常绿针叶林还是亚热带常绿阔叶林都不适合用TG模型来估算GPP;在千烟洲站点的GPP估算中,EC-LUE模型的模拟效果最好,全年低估了17.97%,生长季低估4.81%。表明在亚热带常绿针叶林的GPP估算中适合用EC-LUE模型;在鼎湖山站点的GPP估算中,VPM和MOD17的效果都很好,全年尺度上VPM和MOD17分别低估了7.31%和4.69%,在生长季尺度上,VPM高估了3.72%,MOD17低估了7.36%,结合8 d的GPP模拟说明在亚热带常绿阔叶林的GPP估值中适合使用VPM模型。
由千烟洲站点和鼎湖山站点的实测GPP与各环境参数(EVI、NDVI、LSWI、PAR、LST和Ta)的不同相关性可以看出,各环境参数的相关性的大小对GPP的估算影响巨大。千烟洲观测站点的实测GPP值与各环境参数之间的相关性都很高,前3为Ta、EVI、LST,相关系数分别为0.79、0.72和0.69,鼎湖山观测站点的实测GPP值与PAR的相关系数(0.72)最高,与千烟洲差异很大。因此,可以通过研究各环境参数与不同生态系统的相互作用来提高各模型的模拟精度。
| [1] |
袁文平, 蔡文文, 刘丹, 等. 陆地生态系统植被生产力遥感模型研究进展[J]. 地球科学进展, 2014, 29(5): 541-550. |
| [2] |
陈晓峰, 江洪, 牛晓栋, 等. 季节性高温和干旱对亚热带毛竹林碳通量的影响[J]. 应用生态学报, 2016, 27(2): 335-343. |
| [3] |
Liu Zhengjia, Wang Lunche, Wang Sisi. Comparison of Different GPP Models in China Using MODIS Image and China Flux Data[J]. Remote Sensing, 2014, 6(10): 10215-10231. DOI:10.3390/rs61010215 |
| [4] |
王旭峰, 马明国, 李新, 等. 遥感GPP模型在高寒草甸的应用比较[J]. 遥感学报, 2012, 16(4): 757-762. |
| [5] |
Yuan W, Liu S, Zhou G, et al. Deriving a Light Use Efficiency Model from Eddy Covariance Flux Data for Predicting Daily Gross Primary Production Across Biomes[J]. Agricultural and Forest Meteorology, 2007, 143(3/4): 189-207. |
| [6] |
Running S W, Thornton P E, Nemani R, et al. Global Terrestrial Gross and Net Primary Productivity from the Earth Observing System[M]. New York: Springer, 2000.
|
| [7] |
Sims D A, Rahman A F, Cordova D V, et al. A New Model of Gross Primary Productivity for North American Ecosystems Based Solely on the Enhanced Vegetation Index and Land Surface Temperature from MODIS[J]. Remote Sensing of Environment, 2008, 112(4): 1633-1646. DOI:10.1016/j.rse.2007.08.004 |
| [8] |
王媛, 张娜, 于贵瑞. 千烟洲马尾松人工林生态系统的碳循环模拟及模型参数的敏感性分析[J]. 应用生态学报, 2010, 21(7): 1656-1666. |
| [9] |
王春林, 周国逸, 王旭, 等. 鼎湖山针阔叶混交林生态系统能量平衡分析[J]. 热带气象学报, 2007, 23(6): 643-651. DOI:10.3969/j.issn.1004-4965.2007.06.018 |
| [10] |
杨远程, 郝兴华, 彭碧波, 等. 基于多路径效应的植被覆盖研究[J]. 测绘地理信息, 2014, 39(2): 52-54. |
| [11] |
刘元亮, 李艳, 吴剑亮. 基于LSWI和NDVI时间序列的水田信息提取研究[J]. 地理与地理信息科学, 2015, 31(3): 32-38. DOI:10.3969/j.issn.1672-0504.2015.03.007 |
| [12] |
贾文晓, 刘敏, 佘倩楠, 等. 基于FLUXNET观测数据与VPM模型的森林生态系统光合作用关键参数优化及验证[J]. 应用生态学报, 2016, 27(4): 1095-1102. |
| [13] |
叶子飘, 康华靖, 杨小龙. 不同CO2浓度下番茄幼苗叶片的光能利用效率[J]. 应用生态学报, 2016, 27(8): 2543-2550. |
| [14] |
马敏娜, 袁文平. 青藏高原总初级生产力估算的模型差异[J]. 遥感技术与应用, 2017, 32(3): 406-418. |
| [15] |
陈晋, 唐艳鸿, 陈学泓, 等. 利用光化学反射植被指数估算光能利用率研究的进展[J]. 遥感学报, 2008, 12(2): 2. |
 2019, Vol. 44
2019, Vol. 44

