| LEO空间目标地基甚短弧角度数据初轨确定 |
2. 中国科学院国家天文台长春观测站,吉林 长春, 130117
2. Changchun Observatory, National Astronomical Observatories, Chinese Academy of Sciences, Changchun 130117, China
望远镜光学监测是发现空间新目标的主要手段之一[1, 2],从光学图像提取的角度观测值成为新目标轨道确定的唯一数据。将新目标编目入库的数据处理过程中的第一步为初轨确定[3, 4],在此基础上,联合处理其他数据,获得满足精度要求的轨道参数,实现新目标的编目入库。初轨确定是在没有任何初始信息的前提下,利用单个短弧段的观测数据,采用简单的动力学模型(通常是二体模型)快速计算出空间目标的粗略轨道,后续可以基于该轨道进行改进[5]。新目标监测数据基本上由固定方向监测图像获得,由于监测视场较小,导致低轨目标的观测弧段较短[6, 7],绝大部分情况下不足其周期的百分之一,这样弧长特别短的弧段称为甚短弧。
针对天基甚短弧段初轨确定的问题[8, 9],章品等[10]提出了距离搜索方法,并对该方法进行了相应的仿真实验。结果表明,在处理天基甚短弧段(10~20 s)的初轨确定问题时,该方法在解的成功率和精度上都有明显优势。中科院国家天文台长春人造卫星观测站在2017年建立了由8个小望远镜组成的迷你光电阵,笔者在文献[11]中对该光电阵的观测数据进行了初步分析,弧长的中位数约为41 s。利用光电阵2017年9月12日的观测数据,对距离搜索算法进行测试,分析影响初轨解算成功率和初轨误差。
1 方法距离搜索法的基本过程如下[10]。假设在t1, t2, …, tn时刻分别获得某空间目标的角度观测值:赤经RA1, RA2, …, RAn和赤纬DEC1, DEC2, …, DECn。测站到空间目标方向(即望远镜视线方向)的单位矢量Li(i=1, 2, …, n)为:
| $ \left\{ \begin{array}{l} {L_{{x_i}}} = {\rm{cos}}\left( {{\rm{DE}}{{\rm{C}}_i}} \right){\rm{cos}}\left( {{\rm{R}}{{\rm{A}}_i}} \right)\\ {L_{{y_i}}} = {\rm{cos}}\left( {{\rm{DE}}{{\rm{C}}_i}} \right){\rm{sin}}\left( {{\rm{R}}{{\rm{A}}_i}} \right)\\ {L_{{z_i}}} = {\rm{sin}}\left( {{\rm{DE}}{{\rm{C}}_i}} \right) \end{array} \right. $ | (1) |
式中,Lxi、Lyi、Lzi为Li在天球坐标系下的3个方向的分量。用ρ1、ρn表示t1、tn时刻的观测距离,如果ρ1、ρn已知,可根据ri=ρiLi-Ri(i=1, n)得到两个位置矢量r1、rn,这样纯角度的初轨确定问题就转换为基于两个位置矢量的轨道确定问题,即所谓的初轨确定Lambert问题(利用两个时刻的位置向量计算轨道参数)。可以在一定区间内以一定步长分别假设ρ1、ρn的值,每一个观测值组合可以算出一组轨道参数,并基于此参数计算出其他时刻的角度观测值,并与实际观测值进行比较,根据残差进行判断,从而筛选出可能的定轨结果,再根据半长轴(semi-majora xis, SMA)和偏心率等的分布约束筛选出最优解,限于篇幅,具体的实现流程可参考文献[10]。
2 结果 2.1 观测数据的目标识别笔者根据文献[11]介绍的方法,利用TLE数据和SGP4算法进行观测数据目标识别,即判断该数据是否来自已编目目标,编目目标数据库采用美国公开的TLE数据。2017年9月12日共获得观测弧段3 766个,其中的3 105个弧段可以和现有的1 219个TLE目标关联上,占比为82.45%。1 219个目标的轨道分布如图 1所示。
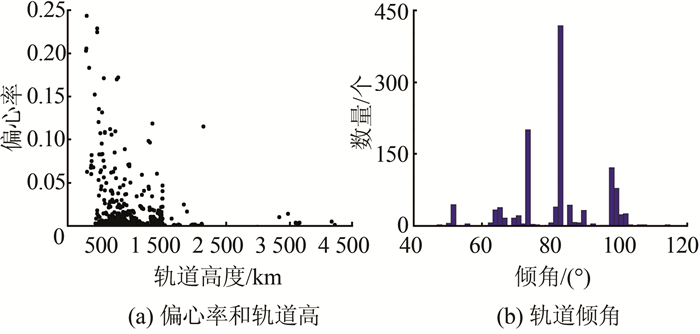 |
| 图 1 空间目标轨道分布 Fig.1 Distribution of Space Objects |
根据图 1可以看出,观测到的目标均为LEO(low earth orbit)目标,轨道高度在4 500 km以下,其中,大部分目标为近圆轨道目标,其轨道高度在500~2 000 km。大部分目标中77.3%的目标偏心率小于或等于0.005,偏心率小于0.05的占到了总数的95.6%。就轨道倾角而言,这些目标的倾角基本在50°~110°,其中86.1%的目标倾角在70°~105°。
2.2 初轨确定结果利用距离搜索法进行初轨确定,分别从初轨确定成功率和初始轨道参数误差的角度进行介绍。首先,利用距离搜索法初轨确定成功率为92.27%。分别对初轨确定成功和失败的观测弧段进行分析,发现定轨失败和成功的弧段的观测值点的个数中位值分别为11和24,对应的弧长分别为18.7 s和40.8 s。考虑到观测弧段弧长对初轨确定的可能影响,分别分析不同弧长区间的初轨确定成功率,结果发现,弧长15~30 s、30~40 s和45~60 s的初轨确定成功率分别为95.3%、96.9%和98.2%。
根据统计结果可以看出,初轨成功率和初轨弧长有较大关系,弧长越长,初轨确定成功率越高。显然,弧长越长观测数据几何结构越强,更有利于解算初始轨道参数;更多的观测值可以解算得到更多可能的轨道参数。
2.3 初轨误差统计得到初始轨道后,利用TLE数据可估计初始轨道参数的误差。分别统计了初轨参数中SMA、偏心率、倾角和升交点赤经(right ascension of ascending node, RAAN)的误差,结果如图 2所示。
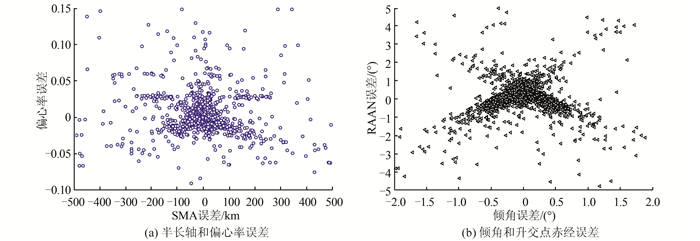 |
| 图 2 初始轨道误差分布 Fig.2 Distribution of IOD Elements Errors |
根据图 2可知,绝大部分初轨SMA误差绝对值小于100 km,据统计约69%的SMA误差小于34 km,偏心率误差绝对值小于0.009,倾角误差小于0.35°,RAAN误差小于0.45°。另外可以发现,轨道倾角误差和RAAN误差近似成线性关系,经计算得到两者的皮尔逊相关系数为-0.35,即两者为弱相关关系。根据倾角误差和RAAN误差可知,初轨参数定出的轨道在空间的位置误差较大,轨道形状误差小一些。
对于某个观测弧段,其已知信息包括角度数据和弧段长度,以及可以估计得到的观测值(赤经、赤纬)变化率。初轨误差和观测弧段的弧长和观测值变化率的分布如图 3所示。
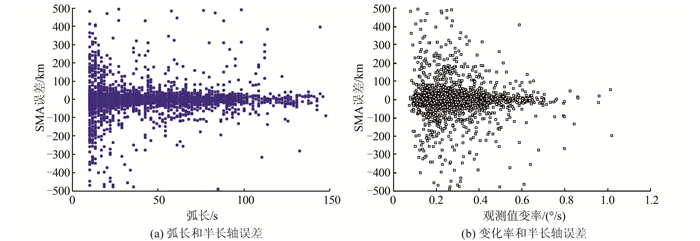 |
| 图 3 初轨半长轴误差和弧段长度及变化率 Fig.3 Distribution of SMA Error, Arc Duration and Change Rate of Observations |
根据图 3可发现,轨道SMA误差随弧长增长而降低;同时,角度观测值变化率主要分布在每秒[0.1°, 0.4°],观测值变化率较小时,SMA有可能出现较大的误差。为详细对比不同弧长条件下,初轨参数误差的大小,分别对不同弧长区间SMA误差进行统计,弧长小于20 s、30 s、60 s和全部弧长的初轨SMA误差分别为80 km、54 km、36 km和34 km。
根据上述统计结果可知,弧长越长得到的初始轨道参数的误差越小。这是因为弧段越长,意味着几何结构越好,相比于更短的弧段,得到的轨道根数更接近真实轨道;另外,根据距离搜索算法的原理,弧长越长在进行初轨计算时可以得到更多的轨道参数。因此,最后筛选时更有可能得到接近真实轨道参数的解。进一步对影响初始轨道计算成功率的因素分析,考虑到观测值变化率不同带来的影响,分别统计了计算成功和失败的弧段的观测值变化率,结果显示,初轨计算失败的显著小于计算成功的弧段的观测值变化率。
综上分析可知,利用距离搜索法计算地基观测数据的初始轨道,其结果和处理天基数据[10]相当,表明该算法具有普适性。
3 结束语长春人造卫星观测站地基迷你光电阵每天可观测到约三、四千个甚短弧段,这些数据可用于空间碎片角度观测数据处理相关算法的验证和改善。本文利用其2017年9月12日的观测数据,对距离搜索算法进行了测试。结果显示,初轨确定成功率约为92.3%,初轨误差和处理天基数据的结果相当。进一步对初轨成功率和参数误差进行了分析,显示弧长越长、观测值角度变化率越大,初轨确定的结果越好。总体而言,距离搜索算法不仅适用于天基观测数据,也适用于地基实测甚短弧角度数据,该算法具有较好的普适性。下一步将考虑如何降低初轨误差并提高初始轨道计算成功率。
| [1] |
魏二虎, 严韦. 太空垃圾实时监测系统建立可行性分析[J]. 测绘信息与工程, 2007, 32(2): 1-4. DOI:10.3969/j.issn.1007-3817.2007.02.001 |
| [2] |
李振伟.空间目标光电观测技术研究[D].长春: 中国科学院研究生院(长春光学精密机械与物理研究所), 2014
|
| [3] |
刘磊.基于天基监视的空间目标测向初轨确定研究[D].长沙: 国防科学技术大学, 2010
|
| [4] |
王秀红, 李俊峰, 王彦荣. 天基照相机监测空间目标定轨方法及精度分析[J]. 光学精密工程, 2013, 21(6): 1394-1403. |
| [5] |
刘林, 张巍. 关于各种类型数据的初轨计算方法[J]. 飞行器测控学报, 2009, 28(3): 70-76. |
| [6] |
张雪敏, 李萌, 熊超. 天基单星测角跟踪条件下的空间非合作目标定轨[J]. 航天控制, 2018, 36(3): 40-45. |
| [7] |
曹坤梅, 曲炜, 刘利生. 实时定轨条件下初轨确定方法研究[J]. 装备指挥技术学院学报, 2003, 14(1): 87-89. DOI:10.3783/j.issn.1673-0127.2003.1.020 |
| [8] |
刘磊, 郗晓宁, 戎鹏志, 等. 一种稀疏测向数据下的天基初轨确定模型及其算法[J]. 宇航学报, 2009, 30(3): 870-876. DOI:10.3873/j.issn.1000-1328.2009.03.007 |
| [9] |
李冬, 易东云, 程洪玮. 天基空间目标监视的短弧段定轨技术[J]. 宇航学报, 2011, 32(11): 2339-2345. DOI:10.3873/j.issn.1000-1328.2011.11.006 |
| [10] |
章品, 桑吉章, 潘腾, 等. 应用距离搜索的低轨空间碎片初始轨道确定方法[J]. 航天器工程, 2017, 26(2): 22-28. DOI:10.3969/j.issn.1673-8748.2017.02.004 |
| [11] |
雷祥旭, 桑吉章, 李振伟. 长春地基光电阵观测数据初步分析[J]. 测绘地理信息, 2019, 44(1): 41-44. |
 2019, Vol. 44
2019, Vol. 44

