| 基于PDR、WiFi指纹识别、磁场匹配组合的室内行人导航定位 |
随着面对公众的位置服务时代的来临及智能手机等移动终端的日益普及,实时、准确的室内定位技术越来越重要[1, 2]。 近年来,随着微机电系统(micro-electro-mechanical,MEMS)技术的发展而产生的MEMS 传感器(如陀螺、加速度计、磁强计)具有成本低(大批量时)、尺寸小、重量轻、功耗低、可靠性高等优点[3],广泛应用于消费类电子产品。行人航迹推算(pedestrian dead-reckoning,PDR)技术利用加速度计和陀螺或磁强计的量测信息能够不断推算用户的位置,因此不依赖于任何外部设备的布设,也不容易受到环境干扰[4]。但是,PDR技术的缺点在于其导航精度因为传感器误差的存在和导航计算中的积分算法,会随着导航距离的增加而降低。
此外,也有学者将室内磁场异常作为一种指纹来用于定位[5]。磁场匹配定位的优势在于不需要任何发射设备,难点在于磁场指纹只有三个维度。为了提高其维度,通常使用批量匹配。批量匹配的方法已经用于室外高精度的重力[6]、地磁[7]以及地形匹配导航[8]。但是,消费电子产品中的惯性传感器误差大,且行人动态复杂,难以挖掘出有效的约束信息(除非将设备固定)。而由于室内环境复杂[9],当前室内磁场匹配技术存在较高的误匹配率,导航误差可能达到数十米,极大地影响用户体验。
针对现有技术的局限性,本文提出一种基于惯性传感器、WiFi指纹识别、磁场匹配组合的室内行人定位系统。
1 PDR、WiFi指纹识别、地磁匹配组合导航算法 本文PDR、WiFi、地磁匹配组合(magnetic matching,MM)导航算法流程如图 1所示。
 |
| 图 1 PDR、WiFi指纹识别、MM组合导航算法流程图 Figure 1 Flow Chart of PDR/WiFi/MM Algorithm |
1.1 数据库建立
传统的逐点采集数据库的建立方法精度较高,但时间和人力成本过高[10]。为节约成本,本文采用走动测量的方式构建数据库,即手持测量设备(智能手机)沿预设轨迹走遍整个区域,通过使用已知路标点(如起点、终点、拐角和路口)的坐标和楼道的方位角信息来修正PDR导航结果,得到整个轨迹上各脚步点的参考位置。本研究中,路标点坐标是通过将室内地图覆盖在Google地球上提取出的,楼道方位角信息由路标点坐标计算得到。
智能手机上WiFi更新率通常较低(如三星手机约为0.3 Hz),因此一旦WiFi数据更新,便将WiFi信号与最邻近脚步点的坐标组合构成一个WiFi指纹。第i个参考点(RPi)上的WiFi指纹为:
| $\begin{align} & \mathbf{F}{{\mathbf{W}}_{i}}=\{\mathbf{po}{{\mathbf{s}}_{i}},\ {{\mathbf{\sigma }}_{pos}}_{i},\ \left( ma{{c}_{i,1}},RS{{S}_{i,1}} \right),\ \ \left( ma{{c}_{i,2}},RS{{S}_{i,2}} \right),\ \cdots , \\ & \ \left( ma{{c}_{i,{{m}_{i}}}},RS{{S}_{i,{{m}_{i}}}} \right)\} \end{align}$ | (1) |
式中,posi和σposi分别为RPi点的坐标及其精度;maci,j和RSSi,j分别为RPi点上接收到的WiFi信号的MAC地址和信号强度;mi为RPi点上接收到的可用WiFi信号的数目。
由于磁强计的高采样率(通常大于10 Hz)不但可将所有脚步点作为参考点,还可在两脚步点间按一定距离内插,将所有内插点作为参考点。第k个参考点(RPk)上的磁场强度指纹为:
| $\mathbf{F}{{\mathbf{M}}_{k}}=\left\{ \mathbf{po}{{\mathbf{s}}_{k}},\ {{\mathbf{\sigma }}_{pos}}_{k},\ {{\mathbf{m}}_{k}} \right\}$ | (2) |
式中,posk 和σposk分别为RPk点的坐标及其精度; mk 为RPk点上的磁场强度指纹。
1.2 WiFi指纹识别算法WiFi指纹识别采用KNN(k-nearest neighbor)算法,通过对比待测点接收到的WiFi信号以及数据库中各参考点的信号,来找到信号强度距离最小(即信号最接近)的k个参考点,然后将k个参考点的位置结合各自的信号强度距离加权平均,计算得到待测点的位置。信号强度距离计算公式为:
| ${{d}_{i}}=\sqrt{\sum\limits_{j=1}^{{{n}_{i}}}{\left| SS_{rec,{{l}_{u}}}^{j}-SS_{DB,i}^{j} \right|}},\ \ i\in {{I}_{RP}}{{n}_{i}}$ | (3) |
式中,di为参考点RPi的信号强度距离;lu为待测点位置;SSrec,lu为 lu点处接收到的WiFi信号;SSDB,i为数据库中RPi点处的WiFi信号;ni为RPi点处收到的WiFi信号数;IRP为数据库中的参考点的集合。利用加权平均求取待测点坐标的计算式为:
| $\mathbf{\hat{r}}=\sum\limits_{i=1}^{k}{\left[ ({{c}_{i}}/C){{\mathbf{r}}_{i}} \right]}$ | (4) |
式中,ci=1/di;C=∑ki=1ci;ri为WiFi信号与待测点WiFi信号第i接近的参考点坐标;为计算得到的待测点坐标。
1.3 磁场匹配将待测点上的磁场指纹与数据库内位置指纹进行匹配,找到最接近的k个位置。所谓“接近”可通过平均距离最小来确定。平均距离计算公式为:
| $MAD=\frac{1}{N}\sum\limits_{i=1}^{N}{\left| {{S}_{i}}-{{M}_{i}} \right|}$ | (5) |
式中,Si是测量轨迹的磁场指纹;Mi为搜索区域内候选轨迹的磁场指纹;N为轨迹的长度。
1.4 行人航迹推算(PDR)PDR算法是一种相对定位方式,通过上一脚步的位置,结合传感器测量或计算出的航向和步长信息,来推算下一脚步的位置。具体的计算公式为:
| $\left[ \begin{matrix} {{\varphi }_{k+1}} \\ {{\lambda }_{k+1}} \\ \end{matrix} \right]=\left[ \begin{matrix} {{\varphi }_{k}}+{{w}_{\varphi ,k}}+[({{s}_{k}}+{{w}_{s,k}})\cos ({{\psi }_{k-1}}+{{w}_{\psi ,k-1}})]/({{R}_{m}}+h) \\ {{\lambda }_{k}}+{{w}_{\lambda ,k}}+[({{s}_{k}}+{{w}_{s,k}})\sin ({{\psi }_{k-1}}+{{w}_{\psi ,k-1}})]/[({{R}_{n}}+h)cos{{\varphi }_{k}}] \\ \end{matrix} \right]$ | (6) |
式中,φ、λ、ψ和s分别为纬度、经度、航向和步长;Rm和Rn分别为子午圈和卯酉圈曲率半径;h为高程;下标k 和k+1 为脚步数;步长模型为sk=A/fk+B+ws,其中fk=1/(tk-tk-1)为走路的频率;tk-1、tk为相邻两脚步的时间;A和B为常系数;wφ,k、wλ,k、wψ,k、ws,k和wb,k分别为纬度、经度、航向、步长和垂向陀螺零偏的噪声。
1.5 信息融合本文使用卡尔曼滤波算法组合PDR、WiFi和磁场匹配,其状态方程和量测方程为:
| $\left\{ \begin{align} & \delta {{\mathbf{x}}_{k+1}}={{\mathbf{\Phi }}_{k+1,k}}\delta {{\mathbf{x}}_{k}}+{{\mathbf{w}}_{k}} \\ & {{\mathbf{z}}_{k+1}}={{\mathbf{H}}_{k+1}}\delta {{\mathbf{x}}_{k+1}}+{{\mathbf{v}}_{k+1}} \\ \end{align} \right.$ | (7) |
式中,
| $\begin{align} & {{\mathbf{\Phi }}_{k+1,k}}=\left[ \begin{matrix} 1 & 0 & \frac{-{{s}_{k}}\sin {{\psi }_{k}}}{{{R}_{m}}+h} & \frac{\cos {{\psi }_{k}}}{{{R}_{m}}+h} & 0 \\ 0 & 1 & \frac{{{s}_{k}}\cos {{\psi }_{k}}}{({{R}_{n}}+h)cos{{\varphi }_{k}}} & \frac{\sin {{\psi }_{k}}}{({{R}_{n}}+h)cos{{\varphi }_{k}}} & 0 \\ 0 & 0 & 1 & 0 & \Delta t \\ 0 & 0 & 0 & 1 & 0 \\ 0 & 0 & 0 & 0 & 1 \\ \end{matrix} \right] \\ & {{\mathbf{x}}_{k}}={{\left[ \begin{matrix} \delta {{\varphi }_{k}} & \delta {{\lambda }_{k}} & \delta {{\psi }_{k}} & \delta {{s}_{k}} & {{b}_{k}} \\ \end{matrix} \right]}^{T}} \\ & {{\mathbf{w}}_{k}}=[{{w}_{N,k}}\ \ {{w}_{E,k}}\ \ \ {{w}_{\psi ,k}}\ \ {{w}_{s,k}}\ \ {{w}_{b,k}}] \end{align}$ |
其中,δφk、δλk、δψk、δsk及bk依次为纬度、经度、航向、步长和垂向陀螺零偏的误差;vk+1为WiFi或磁场匹配相应的量测噪声向量。当WiFi定位结果到上一时刻的组合定位结果的距离小于预设阈值(本文为15 m,即假定组合定位误差均方值RMS为5 m,取三倍RMS值作为阈值)时,认为WiFi定位结果可用,此时,相应的观测向量和观测矩阵分别为${{\mathbf{z}}_{WiFi,k+1}}={{\left[ \begin{matrix} {{{\hat{\varphi }}}_{PDR}}-{{{\tilde{\varphi }}}_{WiFi}} & {{{\hat{\lambda }}}_{PDR}}-{{{\tilde{\lambda }}}_{WiFi}} \\ \end{matrix} \right]}^{T}},{{\mathbf{H}}_{WiFi,k+1}}=\left[ \begin{matrix} {{\mathbf{I}}_{2\times 3}} & {{\mathbf{0}}_{2\times 2}} \\ \end{matrix} \right]$;当磁场匹配结果到上一时刻的组合定位结果的距离小于预设阈值(本文为15 m)时,相应的观测向量和观测矩阵分别为${{\mathbf{z}}_{MM,k+1}}={{\left[ \begin{matrix} {{{\hat{\varphi }}}_{PDR}}-{{{\tilde{\varphi }}}_{MM}} & {{{\hat{\lambda }}}_{PDR}}-{{{\tilde{\lambda }}}_{MM}} \\ \end{matrix} \right]}^{T}},{{\mathbf{H}}_{MM,k+1}}=\left[ \begin{matrix} {{\mathbf{I}}_{2\times 3}} & {{\mathbf{0}}_{2\times 2}} \\ \end{matrix} \right]$ ,${{{\hat{\varphi }}}_{PDR}},{{{\hat{\lambda }}}_{PDR}}$分别为PDR预测得到的纬度和经度;${{{\tilde{\varphi }}}_{WiFi}}$、${{{\tilde{\lambda }}}_{WiFi}}$、${{{\tilde{\varphi }}}_{MM}}$及MM分别为WiFi定位结果的纬度、经度和磁场匹配结果的纬度、经度。 卡尔曼滤波预测公式为:
| $\left\{ \begin{align} & \ \ \ \ \ \ \ \ \delta \mathbf{x}_{k+1}^{-}={{\mathbf{\Phi }}_{k+1,k}}\delta {{\mathbf{x}}_{k}} \\ & \mathbf{P}_{k+1}^{-}={{\mathbf{\Phi }}_{k+1,k}}{{\mathbf{P}}_{k}}\mathbf{\Phi }_{k+1,k}^{T}+{{\mathbf{\Gamma }}_{k}}{{\mathbf{Q}}_{k}}\mathbf{\Gamma }_{k}^{T} \\ \end{align} \right.$ | (8) |
量测方程为:
| $\left\{ \begin{align} & {{\mathbf{K}}_{k+1}}=\mathbf{P}_{k+1}^{-}\mathbf{H}_{k+1}^{T}{{[{{\mathbf{H}}_{k+1}}\mathbf{P}_{k+1}^{-}\mathbf{H}_{k+1}^{T}+{{\mathbf{R}}_{k+1}}]}^{-1}} \\ & \delta {{\mathbf{x}}_{k+1}}=\delta \mathbf{x}_{k+1}^{-}+{{\mathbf{K}}_{k+1}}[{{\mathbf{z}}_{k+1}}-{{\mathbf{H}}_{k+1}}\delta \mathbf{x}_{k+1}^{-}] \\ & \ \ \ \ \ \ \ \ \ {{\mathbf{P}}_{k+1}}=[\mathbf{I}-{{\mathbf{K}}_{k+1}}{{\mathbf{H}}_{k+1}}]\mathbf{P}_{k+1}^{-} \\ \end{align} \right.$ | (9) |
式中,P为待估状态向量δx的协方差矩阵;K为卡尔曼滤波增益矩阵;Q和R分别为状态噪声阵和量测噪声阵;下标k和k+1代表时刻tk和tk+1;上标“-”表示相应项为预测值。
2 实验结果分析利用两组测试数据检验算法的性能,测试所用设备为三星Galaxy S3和S4手机,S3手机用于数据库测绘,S4用于定位实验。两次实验分别在卡尔加里大学的EEEL教学楼和ENB办公楼进行。
2.1 EEEL测试(丰富的WiFi和磁场信号)实验区域面积为140 m × 60 m,WiFi和磁场数据库由4条不同轨迹生成,见图 2,生成的WiFi和磁场数据库见图 3,测试轨迹见图 4,各数字指示了行走顺序。
 |
| 图 2 数据库建立所用轨迹 Figure 2 Trajectories Used to Generate WiFi and Magnetic DBs at EEEL |
 |
| 图 3 EEEL测试生成的WiFi和磁场数据库 Figure 3 Number of Received WiFi Signals and Magnetic Intensity at Each RP in EEEL |
 |
| 图 4 导航测试轨迹 Figure 4 Test Trajectory at EEEL |
卡尔曼滤波状态噪声阵Q、WiFi量测噪声阵RWiFi和磁场匹配量测噪声阵RMM的设定分别为:Q=diag([q2N q2E q2ψ q2s q2b]);RWiFi=diag(vWiFi)和RMM=diag(vMM)。本研究中,qN、qE、qψ、qs和qb的值分别设定为1.56×10-8 rad(通过0.1 m/6 400 km计算得到)、1.80×10-8 rad(通过0.1 m/6 400 km/(cos30°)计算得到)、2°、0.05 m和0.1°/s。var(rWiFi)和var(rMM)均设定为10 m。步长计算公式中参数A和B的值分别为0.36 m/s和0.28 m。
本实验分别计算了PDR、WiFi、磁场匹配、PDR+WiFi组合、PDR+磁场匹配组合以及PDR+WiFi+磁场匹配的联合定位结果。图 5显示了6种方案的定位结果,图 6显示了除PDR外(因为PDR结果随距离不断发散)的5种方案的定位误差图以及定位误差的累计分布函数(cumulative distribution function,CDF),其中红色线标示出了CDF曲线中80%的概率所对应的定位误差值。
 |
| 图 5 PDR 、WiFi、MM、PDR+WiFi、PDR+MM以及PDR+WiFi+MM定位结果 Figure 5 Positioning Results of PDR,WiFi,MM,PDR+WiFi,PDR+MM,and PDR+WiFi+MM |
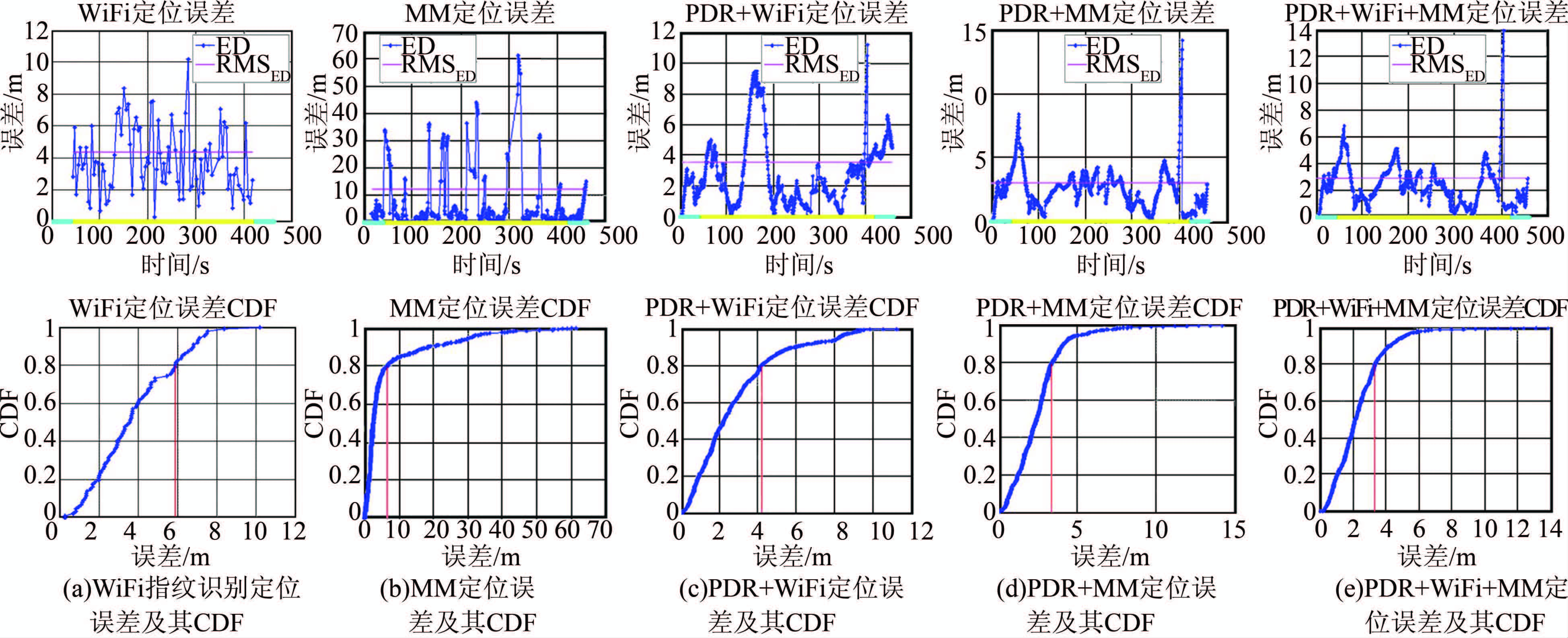 |
| 图 6 5种方案的定位误差图以及定位误差的累计分布函数(CDF) Figure 6 Positioning Errors Distance and Their CDFs for Five Schemes |
可以看出,PDR结果连续且和真实轨迹形状相近,然而,航向误差不断累积并导致位置误差。WiFi能提供绝对位置信息,且误匹配率较低,但结果有明显的波动,这是基于信号强度方法的固有问题。与WiFi相比,磁场匹配结果波动更小,但存在严重的误匹配,因此,磁场匹配的关键是使用其他手段来降低其误匹配。PDR+WiFi、PDR+磁场匹配以及PDR+WiFi+磁场匹配的组合均提供了连续稳定的定位结果,但在400 s处均出现了超过10 m的位置误差。经检查发现,该误差是发生在门口处,这是由于测试者手拉门导致手机姿态出现剧烈变化所致。因此,尽管从长时间尺度上PDR误差会被WiFi或者磁场匹配修正,但短期内PDR误差难以被探测。这也反映了稳健可靠的PDR技术对于组合导航性能的重要性。
为了便于对比,各种方案的位置误差最大值和RMS见表 1。
| 表 1 各种方案的位置误差最大值和RMS/m Table 1 Max Errors and RMSs of Different Schemes/m |
可见,即便是在WiFi指纹识别或是磁场匹配环境较差的ENB实验中,PDR、WiFi、磁场匹配也提供了与EEEL相近的精度。
3 结束语本文提出了一种基于PDR、WiFi指纹识别、磁场匹配组合的室内行人导航定位方法。实测结果表明,在不需额外人工外业工作量的基础上(WiFi和磁场数据库测绘可同时完成),达到比传统惯性+WiFi或惯性+磁场匹配更稳定的导航结果。本方法在WiFi几何分布差或者磁场梯度不明显的环境中仍能提供连续可靠的导航结果。
| [1] |
龚健雅, 王国良. 从数字城市到智慧城市:地理信息技术面临的新挑战[J].
测绘地理信息,2013,39(2) : 1–6.
Gong Jianya, Wang Guoliang. From Digital City to Smart City:New Challenges to Geographic Information Technology[J]. Journal of Geomatics,2013,39(2) : 1–6. |
| [2] |
张华兵, 方志祥, 郭翌寒, 等. 基于实景显著性的行人导航数据模型[J].
测绘地理信息,2015,40(3) : 57–59.
Zhang Huabing, Fang Zhixiang, Guo Yihan, et al. A Saliency-Based Pedestrian Navigation Data Model[J]. Journal of Geomatics,2015,40(3) : 57–59. |
| [3] | El-Sheimy N, Niu X. The Promise of MEMS to the Navigation Community[J]. Inside GNSS,2007,2 : 46–56. |
| [4] | Huang C, Liao Z, Zhao L. Synergism of INS and PDR in Self-contained Pedestrian Tracking with a Miniature Sensor Module[J]. IEEE Sensors Journal,2010,10(8) : 1349–1359. DOI:10.1109/JSEN.2010.2044238 |
| [5] | Xie H, Gu T, Tao X, et al.MaLoc: A Practical Magnetic Fingerprinting Approach to Indoor Localization Using Smartphones[C].The 2014 ACM International Joint Conference on Pervasive and Ubiquitous Computing, Seattle,Washington, USA, 2014 |
| [6] | Golden J P. Terrain Contour Matching (TERCOM): A Cruise Missile Guidance Aid[J]. Proc SPIE,1980,238 : 10–18. DOI:10.1117/12.959127 |
| [7] | Yan L,Cui C.A New Algorithm of Gravity Matching Aided Navigation[C].The 2nd International Conference for Spatial Information Technology, Wuhan,China,2007 |
| [8] | Liu Y, Wu M, Hu X, et al.Research on Geomagnetic Matching Method[C]. The 2nd IEEE Conference on Industrial Electronics and Applications, Harbin, China, 2007 |
| [9] |
朱庆, 熊庆, 赵君峤. 室内位置信息模型与智能位置服务[J].
测绘地理信息,2014,39(5) : 1–7.
Zhu Qing, Xiong Qing, Zhao Junqiao. Indoor Location Information Model and Intelligent Location Service[J]. Journal of Geomatics,2014,39(5) : 1–7. |
| [10] | Bolliger P.Redpin-adaptive, Zero-configuration Indoor Localization Through User Collaboration[C]. The 1st ACM International Workshop on Mobile Entity Localization and Tracking in GPS-less Environments, New York, USA,2008 http://cn.bing.com/academic/profile?id=2130859118&encoded=0&v=paper_preview&mkt=zh-cn |
 2016, Vol. 41
2016, Vol. 41

