| 一种LiDAR平面配准方法辅助的IMU室内定位算法 |
2. 中国地质大学(北京)土地科学技术学院,北京,100083
2. School of Land Science and Technology, China University of Geosciences, Beijing 100083, China
在复杂的室内环境中,由于建筑物的遮蔽,往往无法获得定位卫星信号。相比于全球导航卫星系统(global navigation satellite system, GNSS)定位,惯性导航系统(inertial navigation system, INS)可以不依赖外界信号,通过测量载体在惯性参考系的加速度和角速度,将其对时间进行积分,从而得到载体在导航坐标系中的速度、姿态和位置等信息。但是由于传感器误差的影响,INS得到的位姿误差随时间不断增加。激光雷达(light detection and ranging, LiDAR)在移动过程中可以不断获得周围环境的点云扫描数据,通过对不同位置获得的数据进行匹配,可以得到LiDAR的位移,因此,可以利用LiDAR辅助惯性测量单元(inertial measurement unit, IMU)实现室内高精度定位。
目前,LiDAR和IMU的室内组合导航方法主要是将2D-LiDAR的水平位移和方位角与IMU位姿进行组合,提高室内定位精度。Kohlbrecher等[1]设计了一套以2D-LiDAR扫描匹配结果为基础的实时定位与建图系统,通过扩展卡尔曼滤波(extended Kalman filter, EKF)融合了LiDAR、IMU、GPS和罗盘仪等传感器的观测数据,可以在复杂环境下分析载体的三维实时运动状态,证明了利用EKF融合LiDAR扫描匹配和IMU数据的理论可行性。Kumar等[2]提出了一种室内实时定位建图方案,以无人机为载体,利用IMU和2D-LiDAR数据获得水平位移,利用第二组LiDAR的地面信息获得高度变化,将两组位移信息通过卡尔曼滤波融合,获得无人机的三维轨迹。Tang等[3]将2D-LiDAR扫描匹配得到的航向角、二维位置和IMU数据进行滤波融合,证明在动态条件下,滤波结果比单独LiDAR扫描匹配得到的轨迹精度更高。
随着LiDAR扫描技术的发展,目前出现了大量价格低廉的3D-LiDAR,基于3D-LiDAR的配准方法也在不断成熟。然而,LiDAR配准得到的位移和姿态误差会随着时间不断累积,误差模型难以估计。针对以上问题,本文使用两组3D-LiDAR和IMU,通过基于平面特征的点云配准方法获得Li‐DAR的速度,并利用EKF滤波将其和IMU的位姿推算结果进行数据融合,从而限制IMU位姿推算的误差漂移,以提高室内导航定位的精度。
1 IMU/LiDAR组合导航算法 1.1 IMU误差模型IMU在导航坐标系下的运动学模型公式可参考文献[4], IMU初始对准过程可以参考文献[5]。需要注意的是,本文导航坐标系采用东-北-天(E-N-U)坐标系。考虑到背包载体6自由度的运动情况,系统误差状态向量可表示如下:
| $ \mathit{\boldsymbol{X}}(t) = ({\mathit{\boldsymbol{\delta }}_\varepsilon }, {\mathit{\boldsymbol{\delta }}_v}, {\mathit{\boldsymbol{\delta }}_r}, {\mathit{\boldsymbol{b}}_g}, {\mathit{\boldsymbol{b}}_a}) $ | (1) |
式中,
本文使用的3DM系列航姿参考系统是一种微电子机械系统IMU,其数据误差主要考虑陀螺仪误差和加速度计误差。陀螺仪误差一般包括常值漂移、随机漂移和白噪声分量,可表示成ω(t)=ω0+ωd(t)+wω。其中,ω0为常值漂移;ωd(t)为随机漂移;wω为白噪声。通过IMU长时间静态数据分析,选择一阶马尔可夫过程描述陀螺仪的随机漂移:
| $ {\dot \omega _d}(t) = - \frac{1}{\tau }{\omega _d}(t) + w(t) $ | (2) |
式中,τ指相关时间,是由长时间静态数据分析获得的固定参数;w (t)指白噪声。加速度计误差与陀螺仪误差类似,采用同样的模型估计。
1.2 IMU/LiDAR组合导航IMU的测量坐标系和LiDAR的仪器坐标系存在旋转平移偏差,在进行组合导航前首先进行IMU和LiDAR之间相对位置关系的校准。通过文献[6]中的外参标定方法可获得IMU和LiDAR坐标系相对旋转关系
以往研究证明EKF是一种相对高效且稳定的非线性误差分析方法[7-9],因此本文采用该滤波算法实现IMU和LiDAR的组合导航,流程见图 1。其中,
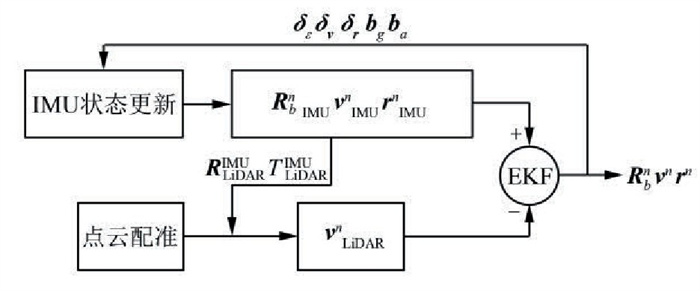 |
| 图 1 IMU/LiDAR组合导航系统流程图 Fig.1 Flow Chart of IMU/LiDAR Integrated Navigation System |
每次滤波过程都包括系统状态更新和观测值更新,具体在组合导航系统中指IMU误差状态的预测更新和基于LiDAR平面配准结果的观测值更新。IMU数据的更新频率和LiDAR数据的更新频率不一致,本文中IMU数据的更新频率是100 Hz,点云数据更新频率是20 Hz。当IMU数据更新时,进行系统位姿推算和系统误差更新;当LiDAR数据更新时,首先利用IMU得到的系统位姿为LiDAR数据提供初始姿态,然后使用文献[10]中的基于平面特征的点云配准方法进行两帧点云之间的旋转平移矩阵计算。在得到相邻三帧点云之间的相对位移后,计算得到中间时刻LiDAR的运动速度
将LiDAR速度作为观测值的系统观测方程为:
| $ {\mathit{\boldsymbol{Z}}_k} = {\mathit{\boldsymbol{H}}_k}{\mathit{\boldsymbol{X}}_k} + {\mathit{\boldsymbol{V}}_k} $ | (3) |
式中,
本文利用组合导航算法进行实验,使用的IMU型号是3DM-GX5-25, LiDAR型号是Velodyne公司生产的VLP-16系列。测量范围为100 m,测量距离精度为±3 cm,竖直方向测量角分辨率为2°,水平方向测量角分辨率为0.1°~0.4°。将两组LiDAR和IMU安装在同一个刚体支架背包上,由实验人员背负支架在实验场景内步行采集数据。
为了给组合导航轨迹提供参考信息,在获得所有点云平面配准关系后,利用图优化(general graph optimization, g2o)对所有关系进行非线性优化,得到一组近似真实轨迹的姿态位移信息,见图 2(a);并且利用这组姿态位移恢复了所有点云的相互位置姿态关系,得到了整个会议室的稠密点云模型,见图 2(b)。从点云模型可以看出,实验场景有足够的平面特征为点云配准提供便利。
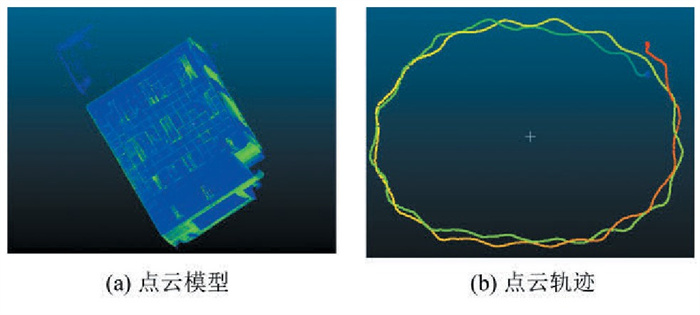 |
| 图 2 g2o生成的点云模型和点云轨迹 Fig.2 Point Cloud Model and Trajectory Generated by g2o |
2.2 实验结果分析
图 3为IMU、LiDAR、参考轨迹的姿态角对比图。可以看出,IMU推算的俯仰角、横滚角相比于LiDAR平面配准得到的姿态角误差更小;IMU推算出的航向角和LiDAR平面配准的航向角误差近似,但是一段时间后,明显还是后者的累积误差更大。出现这种情况是因为实验选取的IMU陀螺仪精度较高,而平面配准的姿态精度容易受所提取平面的噪声影响;而且平面配准存在误匹配和中断的可能性,而陀螺仪的姿态输出可以始终保持不间断。基于这种情况,在EKF的设计中,使用LiDAR的姿态来更正系统姿态误差的方法并不可取。
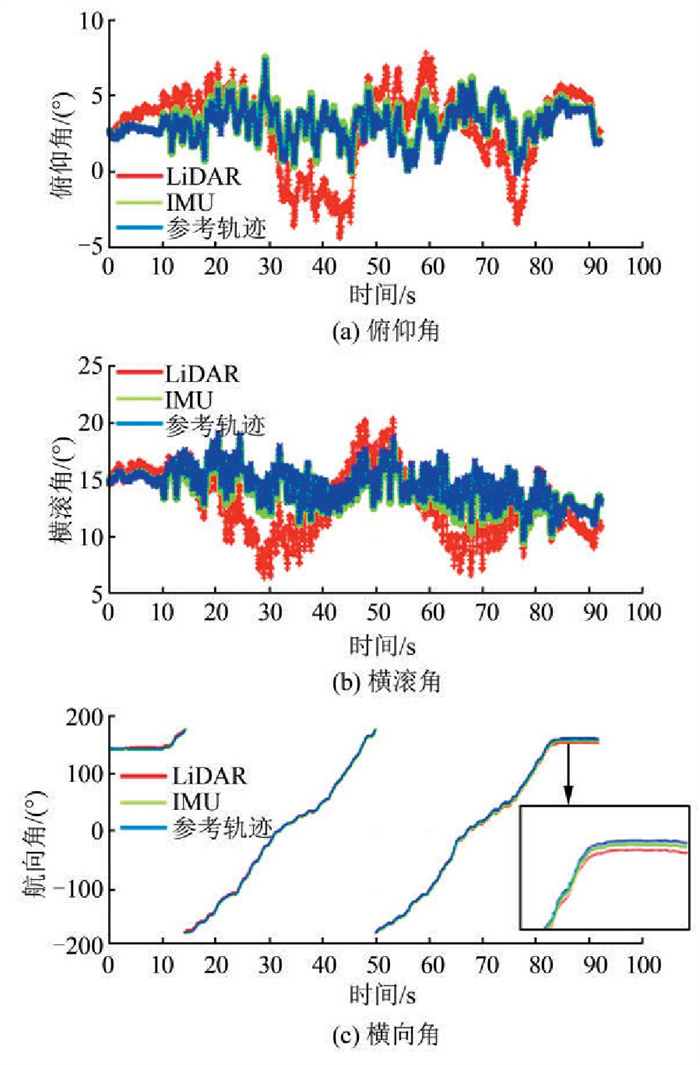 |
| 图 3 IMU、LiDAR、参考轨迹姿态角对比 Fig.3 Attitude Comparison of IMU, LiDAR and Reference Trajectory |
以参考轨迹的水平位置为参考,图 4给出了水平方向上滤波输出的位置误差。LiDAR观测量的加入有效地抑制了滤波的误差漂移,滤波轨迹的水平误差始终控制在0.25 m内。另外,滤波轨迹的水平误差随着轨迹呈周期变化,每次回到起始点时水平误差都趋于零。在图 4框出的最后一段轨迹中,当单独LiDAR配准误差出现较大误差时,滤波误差仍然保持在较小范围内,与参考轨迹保持一致,并没有被观测值的误差所影响。
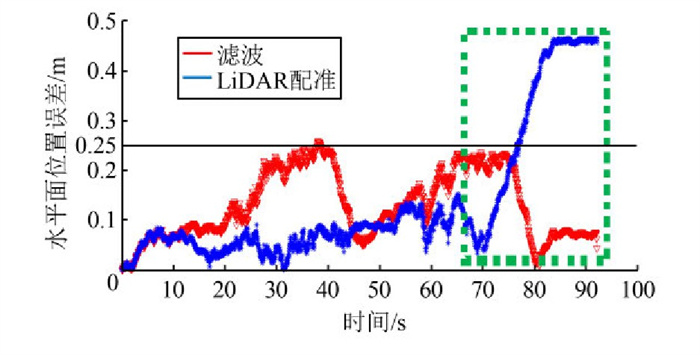 |
| 图 4 水平轨迹误差比较 Fig.4 Comparison of Horizontal Trajectory Errors |
图 5给出了垂直地面方向上滤波输出的位置误差。在轨迹高度误差方面,相比IMU单独导航,虽然组合导航高度误差得到了一定控制,轨迹最后高度误差仍维持在1 m内,但是相比于LiDAR轨迹高度的来回震荡,滤波的轨迹高度始终往一个方向偏离,且高度误差与时间呈线性关系。这是因为相比于水平面的轨迹计算,IMU在竖直方向受到更多重力有害加速度影响,LiDAR的高度观测值无法完全抑制INS的漂移。一般这个问题的解决方式是在垂直地面方向上添加其他约束来进一步抑制INS在高度上的误差,有待进一步研究。
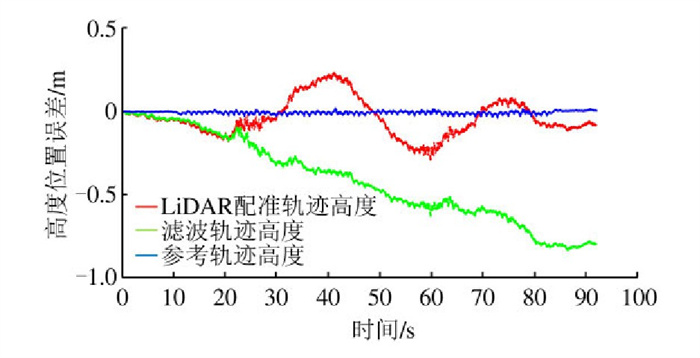 |
| 图 5 滤波、LiDAR、参考轨迹高度变化 Fig.5 Height Variation of Filtering, LiDAR and Reference Trajectory |
以上实验证明,以LiDAR速度为观测值的EKF可以有效地抑制IMU的水平定位误差,并且在LiDAR配准出现较大误差时,滤波也可以将水平误差控制在0.25 m内。
3 结束语本文提出了一种LiDAR平面配准方法辅助的IMU室内定位方法,将LiDAR速度和IMU位姿利用EKF融合,有效约束了误差漂移。实验结果表明:①在动态运动条件下,无论周围环境特征是否丰富,本文采用的IMU姿态比点云配准的姿态更准确,所以即使在一些特征不明显的区域,整个系统始终可以输出准确的姿态;② LiDAR配准得到的LiDAR速度确实限制IMU轨迹的漂移,并且在一些点云配准误差较大的场景,滤波后的结果仍然可以保持一定的水平位移精度;③相较于采用LiDAR的位移和姿态作为观测值的方式,本文将LiDAR速度作为观测值的方案更适合解决实时数据采集中可能遇到的点云配准失效问题。在缺少闭环检测的情况下,LiDAR点云配准获得的位移和姿态都存在误差累积的问题,但是LiDAR的速度误差只和点云配准算法及LiDAR测量精度相关。本文提出的方法可被应用于无GPS信号的室内实时定位导航。
| [1] |
Kohlbrecher S, von Stryk O, Meyer J, et al. A Flexible and Scalable SLAM System with Full 3D Motion Estimation[C]. 2011 IEEE International Symposium on Safety, Security, and Rescue Robotics, Kyoto, Japan, 2011.
|
| [2] |
Kumar G, Patil A, Patil R, et al. A LiDAR and IMU Integrated Indoor Navigation System for UAVs and Its Application in Real-Time Pipeline Classification[J]. Sensors, 2017, 17(6). DOI:10.3390/s17061268 |
| [3] |
Tang J, Chen Y W, Niu X J, et al. LiDAR Scan Matching Aided Inertial Navigation System in GNSSDenied Environments[J]. Sensors(Basel, Switzerland), 2015, 15(7): 16 710-16 728. DOI:10.3390/s150716710 |
| [4] |
严恭敏. 车载自主定位定向系统研究[D]. 西安: 西北工业大学, 2006.
|
| [5] |
捷联惯导在地铁轨道检测中的应用[J]. 测绘地理信息, 2018, 43(1): 55-58. |
| [6] |
Yang Z F, Shen S J. Monocular Visual-Inertial State Estimation with Online Initialization and Camera-IMU Extrinsic Calibration[J]. IEEE Transactions on Automation Science and Engineering, 2017, 14(1): 39-51. DOI:10.1109/TASE.2016.2550621 |
| [7] |
多星座组合精密动态定位的抗差扩展Kalman滤波方法研究[J]. 武汉大学学报·信息科学版, 2015, 40(10): 1 329-1 333. |
| [8] |
Zhao S, Farrell J A. 2D LiDAR Aided INS for Vehicle Positioning in Urban Environments[C]. 2013 IEEE International Conference on Control Applications(CCA), Hyderabad, India, 2013.
|
| [9] |
Fallon M F, Johannsson H, Brookshire J, et al. Sensor Fusion for Flexible Human-Portable Building-Scale Mapping[C]. 2012 IEEE/RSJ International Conference on Intelligent Robots and Systems, Vilamoura-Algarve, Portugal, 2012.
|
| [10] |
Pathak K, Birk A, Vaškevičius N, et al. Fast Registration Based on Noisy Planes with Unknown Correspondences for 3-D Mapping[J]. IEEE Transactions on Robotics, 2010, 26(3): 424-441. DOI:10.1109/TRO.2010.2042989 |
| [11] |
Li R B, Liu J Y, Zhang L, et al. LiDAR/MEMS IMU Integrated Navigation(SLAM)Method for a Small UAV in Indoor Environments[C]. 2014 DGON Inertial Sensors and Systems(ISS), Karlsruhe, Germany, 2014.
|
| [12] |
Deilamsalehy H, Havens T C, Manela J. Heterogeneous Multisensor Fusion for Mobile Platform ThreeDimensional Pose Estimation[J]. Journal of Dynamic Systems, Measurement and Control, 2017, 139(7). DOI:10.1115/1.4035452 |
 2021, Vol. 46
2021, Vol. 46

