| GAMIT数据处理中基线解算模式的对比分析 |
2. 武汉大学卫星导航定位技术研究中心,湖北 武汉,430079;
3. 中国矿业大学,北京, 100083
2. GNSS Research Center, Wuhan University, Wuhan 430079, China;
3. China University of Mining and Technology, Beijing 100083, China
随着GPS技术的快速发展,空间大地测量、地壳运动监测、地球动力学与气候监测、工程测量等都对精密GPS数据处理提出了更高的精度要求,如何获得高精度基线解依然是当前面临的重要问题[1-4]。GAMIT软件是世界上最优秀的GPS定位和定轨软件之一,具有高精度和高稳健性的特征。当采用精密星历和高精度起算点坐标时,长基线相对精度能达到10-9量级,短基线的精度也能够达到1 mm。同时,由于其具有解算速度快、持续升级等优点,已在国内外得到广泛使用[5]。
当前,国内外学者对影响GAMIT软件基线解算精度的各种因素进行了研究。张双成等利用相邻点间基线长度均为3 m的3个点对不同短基线模型进行了分析[5];姜卫平等对星历误差、起算点坐标等对基线解算的影响进行了研究[6]。由于缺乏对不同基线解算模式及其适用范围的研究,因此对GAMIT数据处理中基线解算模式的对比分析是极为必要的。
本文利用不同范围内的基线组成同步闭合环,以标准化的均方根误差(NRMS)、基线重复性等对两种处理模式BASELINE、RELAX的基线解算结果进行对比分析,得出有意义的结论。
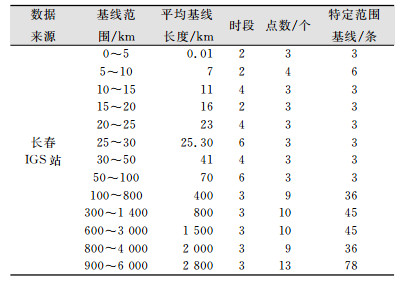
1 基线选取及GAMIT基线解算模式介绍 1.1 基线数据选取为了利用GAMIT软件进行高精度GPS基线解算,本文采用两种处理模式BASELINE、RELAX对不同长度的基线进行解算,并分析结果。为使结果更有代表性,选取各时段的基线长度均在相应的基线长度范围内,如表 1所示。
| 表 1 基线介绍 Table 1 Introduction of Baseline |
 |
1.2 GAMIT基线解算模式介绍
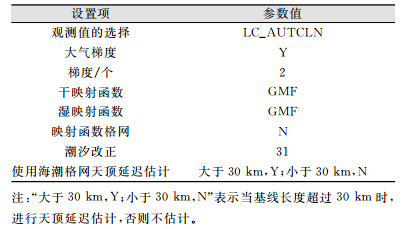
基于GAMIT软件进行高精度基线解算时,依据GPS数据处理的多样性,该软件提供了多种参数选择,以确保稳定可靠的GPS定位结果。本文在处理表 1中的基线时,选用的主要参数设置项如表 2所示。
| 表 2 控制参数的选择 Table 2 Selection of Control Parameters |
 |
进行高精度静态GPS相对定位时,依据对卫星轨道参数的设置,GAMIT提供了两种处理模式:①BASELINE不包含轨道或地球定向参数,可用来固定轨道;②RELAX包含测站、轨道和地球自转参数,需要设置先验约束(轨道坐标、各方向的约束值和1%的直接辐射压、y-偏差系数、1%的第三轴系数等)。依据表 2中的相关参数值,基于GAMIT软件分别采用BASELINE和RELAX两种解算模式对表 1中的基线进行处理。
2 两种解算模式结果对比分析采用上述的数据和解算方法,分别采用BASELINE和RELAX两种处理模式进行解算,得到基线解算结果文件。下面将从标准化的均方根误差(NRMS)、基线精度、基线重复性和基线较差方面对两种处理模式进行对比分析。
2.1 标准化的均方根误差和解算精度的比较和分析标准化的均方根误差(NRMS)是衡量基线解算质量的最主要的指标之一。进行高精度基线解算时,要求NRMS的值小于0.3,如图 1所示,两种处理模式下NRMS差别很小,且都小于0.3,满足精密基线解算的要求[7]。
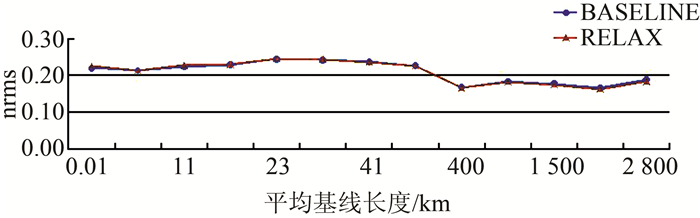 |
| 图 1 BASELINE和RELAX模式下NRMS值对比 Figure 1 Contrast of nrms in BASELINE/RELAX |
根据基线处理结果,绘制相应的精度随基线长度变化的曲线图,如图 2所示,因所选基线及时段较多,根据本文目的,选择精度的平均值做对比。
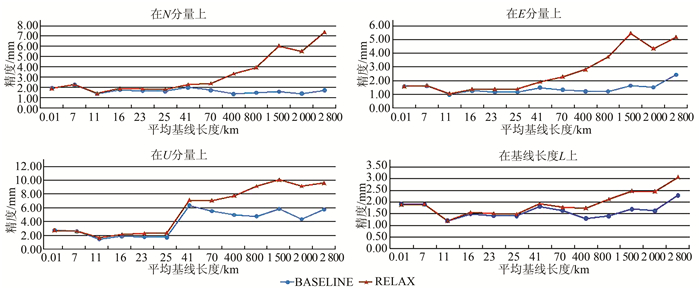 |
| 图 2 两种处理模式的精度对比 Figure 2 Accuracy Comparison of Two Processing Modes |
图 2中,两种处理模式各分量上的精度,当基线长度小于100 km时,差异在1 mm以内,当基线长度大于100 km时,差异随着基线长度的增加而增大;在U分量方向上,精度差异较大;BASELINE的解算精度较为稳定,RELAX解算精度的波动性较大。因此,对于长度大于100 km的基线,BASELINE模式解算精度较高。
2.2 基线重复性的比较与分析基线重复性是衡量数据处理质量的重要指标之一,用同一基线两种方法的基线较差来计算统计意义下的重复性,可以用下式计算基线向量的重复性Rl为[8]:
| $ \left\{ {\begin{array}{*{20}{l}} {{R_l} = {{\left[{\frac{{\frac{n}{{n-1}}\sum\limits_{i = 1}^n {\frac{{{{\left( {{L_i}-\bar L} \right)}^2}}}{{\delta _i^2}}} }}{{\sum\limits_{i = 1}^n {\frac{1}{{\delta _i^2}}} }}} \right]}^{1/2}}}\\ {\bar L = \sum\limits_{I = 1}^N {\frac{{{L_i}}}{{\delta _i^2}}/\sum\limits_{i = 1}^n {\frac{1}{{\delta _i^2}}} } } \end{array}} \right. $ | (1) |
式中,L为单日解基线分量(或边长)的加权平均值;n为单日解数目;Li为第i日的基线分量(或边长)。利用式(1)可分别求出基线在3个分量方向和基线长度方向的重复性。为方便比较两种处理模式的差异和优劣,画出重复性随基线长度变化的折线图,如图 3所示。
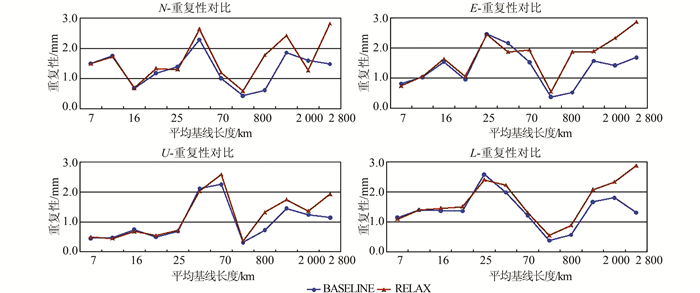 |
| 图 3 两种处理模式的重复性对比 Figure 3 Repeatability Comparison of Two Processing Modes |
由图 3可知,两种处理模式的重复性差别不大(最大不超过2 mm)。基线长度小于400 km时,两者几乎重合;基线长度大于400 km时,BASELINE模式解算基线的重复性优于RELAX模式。
2.3 基线较差的比较与分析如图 4所示,基线较短时,两种处理模式的基线较差很小,表明基线向量差别小;当基线较长时,差别较大。
 |
| 图 4 加权平均基线较差 Figure 4 Baseline Difference of Weighted Average |
当基线较长时,利用解算历元时刻发布的IGS站的精确坐标作为真值,反算出站点之间在X、Y、Z三个方向的基线分量,并与GAMIT所求基线分量做对比,结果如图 5所示,限于篇幅,仅列出Z方向基线差,横坐标如ajac bzrg表示测站ajac与测站bzrg之间的基线。
 |
| 图 5 Z方向基线差对比 Figure 5 Contrast of Baseline Difference in Z Direction |
从图 5可以看出,当平均基线长度为400 km、800 km时,两种处理模式的解算结果与真值吻合得很好;随着平均基线长度的增加,RELAX的吻合度越来越差,如2 800 km时,差距已非常明显。因此在长基线数据处理中,BASELINE模式的解算效果较好。
3 结束语笔者通过采用BASELINE、RELAX两种模式对每个时段的基线长度均在特定范围内的同步闭合环进行高精度基线解算,从解算结果的NRMS、基线平均精度、基线重复性和基线较差4个方面进行比较,得出以下结论:①NRMS均小于0.3,说明BASELINE和RELAX两种处理模式的解算结果均满足高精度基线解算的基本要求;②对于中、短基线而言,BASELINE模式和RELAX模式从基线精度、基线重复性和基线较差等方面看都相差甚微;③基线较长时,BASELINE模式在平均精度、基线重复性和在与真值的对比等方面均比RELAX模式好;因此,在中、短基线(小于100 km)数据处理中,两种处理模式都可以选择;当基线较长(大于100 km)时,BASELINE的解算模式较好。
| [1] |
蒋志浩, 张鹏, 秘金钟, 等. 基于CGCS2000的中国地壳水平运动速度场模型研究[J].
测绘学报,2009,38(6) : 471–476.
Jiang Zhihao, Zhang Peng, Bi Jinzhong, et al. The Model of Crustal Horizontal Movement Based on CGCS2000 Frame[J]. Acta Geodaetica et Cartographica Sinica,2009,38(6) : 471–476. |
| [2] |
朱建树, 许超钤. 利用北海CORS监测大气可降水量的应用研究[J].
测绘地理信息,2015,40(5) : 36–38.
Zhu Jianshu, Xu Chaoqian. Applied Research of Monitoring Precipitable Water Vapor by Using Beihai CORS[J]. Journal of Geomatics,2015,40(5) : 36–38. |
| [3] |
谢树明, 潘鹏飞, 周晓慧. GPS坐标时间序列共模误差空间特性分析[J].
地理空间信息,2014,12(4) : 44–54.
Xie Shuming, Pan Pengfei, Zhou Xiaohui. Spatial Characteristics Analysis of Common Mode Error in GPS Coordinate Time Series[J]. Geospatial Information,2014,12(4) : 44–54. |
| [4] |
吴伟伟.华北地区GPS连续站坐标时间序列特征研究[D].北京:中国地震局地震预测研究所, 2014 Wu Weiwei. Insight into the Characteristics of GPS Time Series in North China[D]. Beijing: Institute of Earthquake Science, China Earthquake Administration, 2014 http://cdmd.cnki.com.cn/Article/CDMD-85405-1014316479.htm |
| [5] |
张双成, 曹海洋, 高涵, 等. 基于GAMIT的GPS短基线解类型分析及应用[J].
测绘通报,2011,(10) : 27–29.
Zhang Shuangcheng, Cao Haiyang, Gao Han, et al. Application and Analysis of GPS Short Baseline Processing Based on GAMIT[J]. Bulletin of Surveying and Mapping,2011,(10) : 27–29. |
| [6] |
姜卫平, 刘经南, 叶世榕. GPS形变监测网基线处理中系统误差的分析[J].
武汉大学学报·信息科学版,2001,26(3) : 196–199.
Jiang Weiping, Liu Jingnan, Ye Shirong. The Systematical Error Analysis of Baseline Processing in GPS Network[J]. Geomatics and Information Science of Wuhan University,2001,26(3) : 196–199. |
| [7] |
韩艳, 高雅萍, 张双成. GAMIT10.40软件处理GPS数据高精度的探讨[J].
西部探矿工程,2012,(3) : 159–161.
Han Yan, Gao Yaping, Zhang Shuangcheng. Discussion on the High Precision of GPS Data Processing by GAMIT10.40 Software[J]. Mineral Exploration Projects in West China,2012,(3) : 159–161. |
| [8] |
鄂栋臣, 詹必伟, 姜卫平, 等. 应用GAMIT/GLOBK软件进行高精度GPS数据处理[J].
极地研究,2005,17(3) : 173–182.
E Dongchen, Zhan Biwei, Jiang Weiping, et al. High-precision GPS Data Processing by GAMIT/GLOBK[J]. Chinese Journal of Polar Research,2005,17(3) : 173–182. |
 2016, Vol. 41
2016, Vol. 41

