| 任意旋转角三维空间直角坐标转换的迭代算法 |
2. 河北省水利水电勘测设计研究院,天津, 300250
2. Hebei Research Institute of Investigation and Design of Water Conservancy and Hydropower, Tianjin 300250, China
传统的三维空间直角坐标转换均是在假设旋转角为微小量时将非线性模型转化为线性模型求解7参数,如莫洛金斯基模型、布尔莎转换模型、武测模型等,这些模型只适用于小旋转角的转换(如西安80坐标系、北京54坐标系与WGS84坐标系间的转换),而工程坐标系与地方坐标系或国家坐标系转换、三维可视化不同视角的空间坐标变换,摄影测量中空间共线方程建立及后方交会等都要进行坐标转换,这些都是大旋转角变换,此时,用传统模型将产生较大的模型误差。为此,很多学者对大旋转角坐标变换进行了大量研究[1-7]。姚宜斌等[8]提出了大角度的三维基准转换参数求解模型;曾怀恩等[9]对三维坐标转换的非线性模型不作线性化处理,采用了一种直接搜索法求解模型参数;王传江等[10]提出了在3个或3个以上公共点时,通过构建辅助公共点,实现大旋转角的坐标转换。当前,大旋转角7参数解算模型仍存一定的局限性和近似性,转换参数求取过程中模型病态问题和迭代收敛速度慢等依然是研究热点。本文在传统三维坐标转换基础上,提出了迭代法精密求解转换参数的算法,该方法不仅适合小旋转角也适用于大旋转角的三维坐标转换,具有计算过程简便、收敛速度快、不依赖7参数的初值、计算结果精确、便于程序实现等特点。
1 三维直角坐标精密转换模型与转换参数的迭代算法传统的三维直角坐标转换模型为:
| $ {\left[ \begin{array}{l} X\\ Y\\ Z \end{array} \right]_{{\rm{New}}}} = \left[ \begin{array}{l} \Delta X\\ \Delta Y\\ \Delta Z \end{array} \right] + k\mathit{\boldsymbol{R}}{\left[ \begin{array}{l} X\\ Y\\ Z \end{array} \right]_{{\rm{Old}}}} $ | (1) |
式中,[X Y Z]NewT表示经坐标转换后的新坐标系统下的坐标;[X Y Z]OldT表示旧坐标系统下的坐标;[ΔX ΔY ΔZ]T为平移因子;k为尺度缩放因子;R为坐标旋转矩阵。坐标旋转矩阵R构成过程为:首先将坐标轴绕X轴逆时针旋转Φ,得旋转矩阵RX;再将坐标轴绕新的Y轴逆时针旋转Ψ,得旋转矩阵RY,最后将坐标轴绕新的Z轴逆时针旋转Ψ,得旋转矩阵RZ;将以上3次旋转合并即可得坐标旋转矩阵R。
若新旧坐标系下有3个以上(含3个)的基准点,则可按最小二乘准则进行迭代计算,即可求解7参数的最优估值。其评定精度为:
| $ {\sigma _0} = \sqrt {{\mathit{\boldsymbol{V}}^{\rm{T}}}\mathit{\boldsymbol{PV}}/f} $ | (2) |
式中,f为自由度,此时f=3n-7,n为公共点个数。
转换参数的迭代算法如下。
1) 任意设定7参数初值,并给定参数改正数的限差,迭代结束的条件设定为:旋转参数1×10-3 s, 平移参数1 mm, 尺度参数1×10-7。
2) 整理参数值,计算新旧坐标旋转矩阵和新旧坐标标差值,组成误差方程。若有n个公共点,则组成3n个误差方程。
3) 用最小二乘法求取7参数的改正数x(k+1)(k为迭代次数)。
4) 检核参数的改正数是否小于给定的限差,若不符合限差,则将X(k)=X(k-1)+x(k)作为新的初值,重复步骤1)~步骤4);符合限差时,迭代结束,将X(k)作为参数最佳估值。
2 算例分析 2.1 算例1文献[8, 9]均以广州新机场航站楼网构件实例对坐标转换方法进行研究。该例设计坐标系为右手系,测量坐标系为左手系。为计算方便,设计坐标系Z与Y坐标对调,将设计坐标系记为X′(X)向北,Y′(Z)向东,Z′(Y)向上,此时两坐标系统统一到左手系。
采用本文算法,17个公共点全部参与解算,按最小二乘法,可得由xyz坐标系转到X′Y′Z′的平移参数为[-109.110 147, -96.496 681, -101.334 650]T, 旋转参数θ=1′41.414 9″,Φ=11′27.409 2″,Ψ=1′00.081 7″,比例尺k=1.002 025 37,计算得到单位权中误差m0=8.16 mm,迭代参数为3次,与文献[1]比较,内符合精度一致,迭代次数有所降低,参数解算收敛速度较快,优于文献[1]的算法。
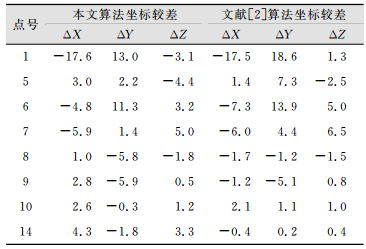
为比较坐标转换后的外附合精度,与文献[9]同样以8、10、14等3个公共点解算转换参数,再用求得的转换参数将实测坐标转换到设计坐标,与已知坐标较差得到的外附合精度为15.9 mm,转换精度与文献[8]一致,优于文献[2]的转换精度。利用本文算法与文献[9]算法分别求取的坐标较差数据如表 1所示。
| 表 1 转换后的节点坐标较差/mm Tab.1 Difference Between Transformed Node Coordinates/mm |
 |
2.2 算例2
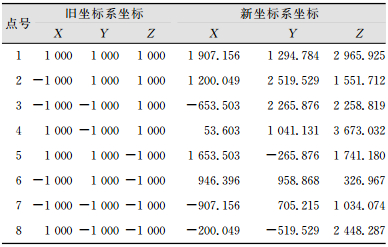
以文献[9]中的模拟数据为例。已知点1~8分别为立方体的8个顶点,他们的坐标已知(表 2)。设这些点沿X轴平移500 m,沿Y轴平移1 000 m,沿Z轴平移2 000 m,分别绕X、Y、Z轴旋转30°、45°、60°,尺度参数为1,变换后的坐标见表 2。
| 表 2 模拟数据/m Tab.2 Simulated Data/m |
 |
为分析初值选取对解算转换参数精度及计算速度的影响,分别选取以下3种初始值方案(表 3)。
| 表 3 旋转角、坐标平移量、长度比初始值变化时转换参数计算结果 Tab.3 Change when Initial Value of the Rotation Angle, Coordinate Translation, Length Factor the Results of Transformation Parameters |
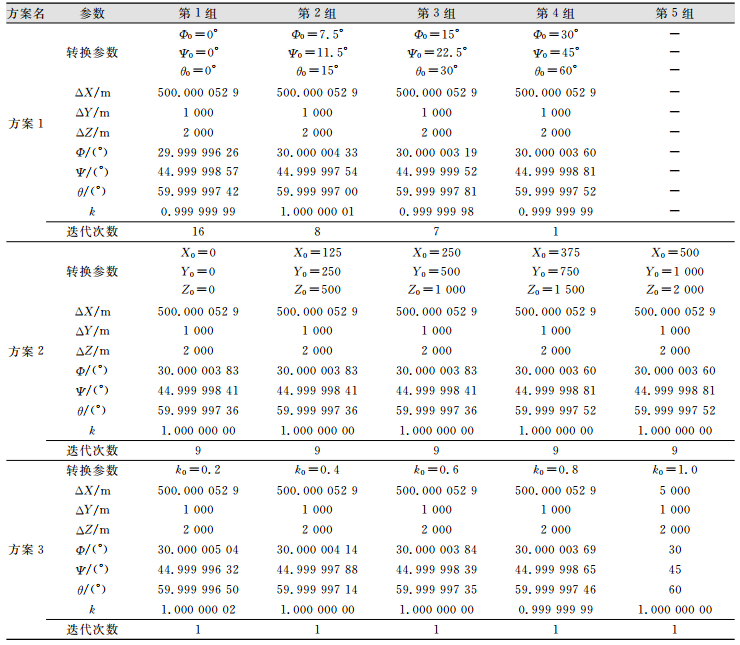 |
方案1 坐标平移量均为0,尺度比为1,X、Y、Z轴旋转角选取4组数据。
方案2 X、Y、Z轴旋转旋角都为10°,尺度比为1,X、Y、Z轴平移量选取5组数据。
方案3 X、Y、Z轴旋转旋角为30°、45°、60°,X、Y、Z轴平移量均为100,尺度比按0.2递增,选取5组数据。
表 3的计算结果表明,7参数的初值无论如何选取,解算的转换参数均可达到预期精度,由此可见,本文算法对于7参数解算不依赖于初始值大小。迭代次数与旋转角初始值的大小有关,初始值越接近真值,迭代次数越少。因此旋转角初始值影响参数计算速度。
3 结束语本文提出的三维空间直角坐标转换的精密迭代算法适用于任意大小旋转角的三维坐标转换,不依赖于初始值的大小,参数计算精度高,解算稳定,收敛速度快,易于编程实现,可解决实际工程中多类型三维空间直角坐标转换问题[10],具有较高的推广应用价值。
| [1] |
罗长林, 张正禄, 邓勇, 等. 基于改进的高斯-牛顿法的非线性三维直角坐标转换方法研究[J]. 大地测量与地球动力学, 2007, 27(1): 50-54. |
| [2] |
潘国富, 鲍志雄, 金永新. 7参数模型完整公式及简化公式的适用性研究[J]. 导航定位学报, 2013, 1(2): 34-37. DOI:10.3969/j.issn.2095-4999.2013.02.008 |
| [3] |
许超钤, 姚宜斌, 熊思婷, 等. 三维任意旋转角度坐标转换的整体最小二乘回归解法[J]. 测绘信息与工程, 2010, 35(5): 46-48. |
| [4] |
王海青, 张永超. 关于空间直角坐标转换中的病态问题的探讨[J]. 科技传播, 2013, 5(1): 110-111. |
| [5] |
刘志平, 杨磊. 大旋转角的空间直角坐标转换方法的改进[J]. 大地测量与地球动力学, 2016, 36(7): 586-590. |
| [6] |
潘国荣, 汪大超, 周跃寅. 两种大转角空间坐标转换模型研究[J]. 山东科技大学学报(自然科学版), 2015, 34(1): 61-67. DOI:10.3969/j.issn.1672-3767.2015.01.010 |
| [7] |
尹晖, 王晶晶, 田鑫. 三维空间基准转换公共点选取的新方法[J]. 测绘地理信息, 2016, 41(2): 14-17. |
| [8] |
姚宜斌, 黄承猛, 李程春, 等. 一种适用于大角度的三维坐标转换参数求解算法[J]. 武汉大学学报·信息科学版, 2012, 37(3): 253-256. |
| [9] |
曾怀恩, 黄声享. 三维坐标转换参数求解的一种直接搜索法[J]. 武汉大学学报·信息科学版, 2008, 33(11): 1118-1121. |
| [10] |
王传江, 王解先, 顾建祥. 大旋转角三维直角坐标转换的一种线性模型[J]. 铁道勘察, 2012, 38(6): 4-6. DOI:10.3969/j.issn.1672-7479.2012.06.003 |
 2019, Vol. 44
2019, Vol. 44

