| 基于决策树对有无降水进行预测 |
在全球变暖的背景下,海陆热力差异发生了改变,使得大尺度环流结构也发生了改变,加剧区域以及全球的水循环进一步影响降水的空间分布。地表蒸发也会随着地表温度的升高而增加,而且温度的升高还会增强大气保持水分的能力[1]。研究过去50年的降水资料发现,西南地区8~12月降水的比例减少; 长江中下游及华南地区春秋降水比例降低,而冬夏季降水比例增加[2]。气象数据呈现多源性、多样性的特点[3]。
面对大量的气象数据,基于统计理论的相关分析方法和回归方法仍然在降水的预测预报中发挥着重要作用[4]; 模式输出统计方法是一种被广泛采用进行天气预报的方法,但是在降水这类反映大中小尺度综合效应的天气时,预报效果比较差[5]; 利用数据挖掘处理具有非线性相关特征的降水时,具有比较大的优势[4, 6, 7]。
文献[8, 9]利用SLIQ(supervised learning in quest)决策树对是否降水进行预测,将地表温度、大气压强、风速、水汽压和露点温度作为降水的属性,分别利用基于Gini指数和基于信息熵的SLIQ决策树方法对降水进行预测,前者的准确度是72.30%,后者的准确度是74.92%[8, 9]。本文选取数据挖掘中的C4.5决策树和随机森林,把是否有降水作为预测的对象。随机森林利用装袋(bagging)有放回抽样技术从原始样本中抽取多个样本,继而在每个样本上训练基决策树,最后组合这些决策树的预测,通过投票的方式对新的未分类样本进行预测,具有很高的预测准确度[10]。
1 降水预测本文从ECMWF(European Center for Medium Range Weather Forcast)下载2000-2014 (15 a)的地表温度、大气压强、风速、大气可降水量、露点温度和降水量的日平均数据,每一天的气象数据为一条记录。将地表温度、大气压强、风速、大气可降水量和露点温度作为属性特征; 降水作为数据记录的类标号,类标号的值是有或无。
1.1 决策树决策树是一种树结构。其中,树的最顶层节点是根节点,每一个非叶节点表示在一个属性上进行测试,每一个分支表示一个测试输出,在每一个叶节点存放一个类标号[11]。
C4.5决策树和SLIQ决策树的不同之处在于非叶节点(根节点和内部节点)的划分标准。非叶节点的划分标准一般根据其子女节点的不纯性来度量。不纯性度量为:
| $ {\rm{Entropy}}\left( t \right) =-\sum\limits_{i=1}^c {p\left( {i\left| t \right.} \right)} {\log _2}\left( {p\left( {i\left| t \right.} \right)} \right) $ | (1) |
| $ {\rm{Gini}}\left( t \right) = 1- \sum\limits_{i=1}^c {{{\left[{p\left( {i\left| t \right.} \right)} \right]}^2}} $ | (2) |
式中,t表示即将划分的非叶节点; c表示分成的类的个数; p(i|t)表示在t节点中类i的概率。
信息熵、基尼指数越高,节点的不纯性越高,对节点划分的最好结果是子女节点有很低的不纯性。利用当前节点和其子女节点的不纯性的差可以确定根据何种属性对当前节点进行划分,也就是信息增益Δinfo:
| $ {\mathit{\Delta } _{{\rm{info}}}} = I\left( {{\rm{parent}}} \right)-\sum\limits_{j = 1}^k {\frac{{N\left( {{v_j}} \right)}}{N}I\left( {{v_j}} \right)} $ | (3) |
式中,I(·)是给定节点的不纯性度量; k是分类的个数; N是父节点上的记录总数; N(vj)是与vj相关的记录个数。父节点的不纯性度量I(parent)是固定的,要使得信息增益Δinfo最大,即是要子女节点的不纯性度量I(vj)最小。
信息增益Δinfo作为划分标准,会倾向于有更多取值的属性,即有更多的vj值。由于与vj值有关的记录数量变小,N(vj)/N、I(vj)显然变小,信息增益Δinfo变大。C4.5对划分标准进行了改进,采用的是信息增益率(gain ratio):
| $ G = \frac{{{\mathit{\Delta }_{{\rm{info}}}}}}{S} $ | (4) |
其中,划分信息
随机森林是一种组合分类器。它的主要原理是:采用固定的概率分布从原始样本中产生K个随机样本,这K个随机样本独立同分布; 然后,在这K个样本上训练基分类器,其中划分非叶节点时,在随机选取的log2M个属性中挑选最佳划分点,继而生成K颗独立的决策树; 最后组合多棵决策树做出的预测,采用投票的方式对新的样本进行分类。随机森林的流程如图 1所示。
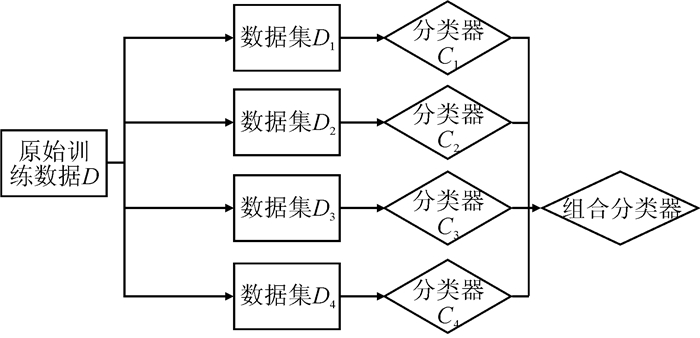 |
| 图 1 随机森林构建流程图 Figure 1 Flow Chart of Random Forest Construction |
1.2 决策树在降水预测中的实现
C4.5决策树、SLIQ以及随机森林的基分类器运用不同的标准对非叶节点进行划分,生成单棵决策树的具体步骤如图 2所示。
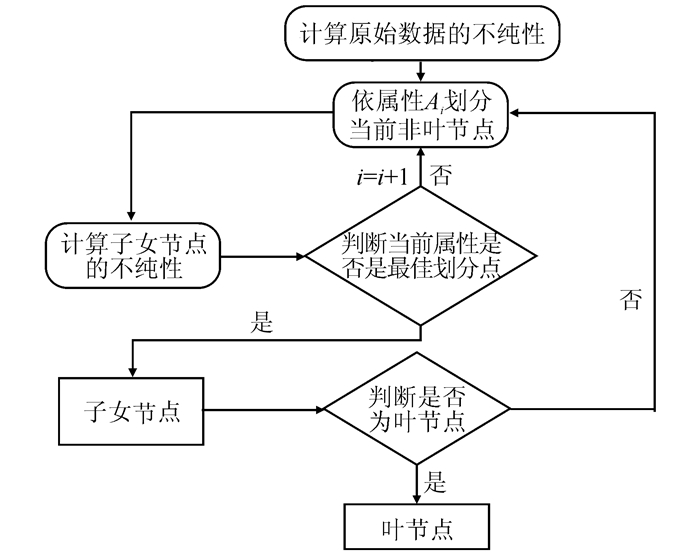 |
| 图 2 决策树生成流程图 Figure 2 Flow Chart of Decision Tree Construction |
1) 对于根节点(当前节点),先算出每类(无降水、有降水)的概率PN、PY,利用式(1) 算出其信息熵值Eparent;
2) 考虑某个属性Ai,将当前节点划分为子女节点,依据式(1) 计算子女节点的信息熵值,利用式(3) 和式(4) 计算信息增益和信息增益率,判断是否为最佳划分,若不是最佳划分,考虑其他属性值;
3) 判断由最佳划分得到的子女节点是否为叶节点。如果不是,则重复步骤2),对当前节点进行划分;
4) 重复步骤3),直至所有的测试记录都从属于一个叶节点[11]。
2 不同决策树预测准确度比较本文分别选取不同数量的数据记录作为训练数据,利用不同的决策树,采用10-折交叉验证(K=10) 方法评估决策树的性能,也即得到决策树的预测准确度(利用软件WEKA实现)。结果如图 3所示。
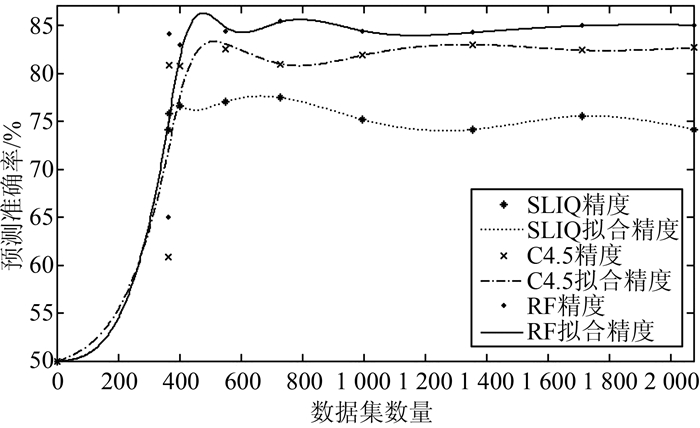 |
| 图 3 基于不同决策树对不同数据集的预测准确率 Figure 3 Forecast Accuracy of Different Decision Trees to Different Data Sets |
由图 3可以得到,随着数据量的持续增大,3种算法的预测准确度趋于平稳; 在预测准确度平稳后,随机森林的平均预测准确度为84.36%,C4.5决策树的为82.63%,基于信息熵的SLIQ的为75.11%;随机森林和C4.5决策树的平均预测准确率明显高于SLIQ的。
C4.5决策树和SLIQ决策树的主要区别在于划分根节点和内部节点时采用的不纯性指标。采用信息增益率来寻找最佳划分能够克服使用信息增益带来的问题,进而提高预测准确率。随机森林通过在原数据集中构建随机样本,训练基决策树,通过综合基决策树的分类信息确实能够增加预测的准确度。但是不同于SLIQ大幅提高预测准确率的是,随机森林的平均预测准确率只比C4.5决策树提高1.73%,而随机森林在构建模型时所消耗的时间却是C4.5的几十倍。如图 4所示,随着数据量的增加,随机森林和C4.5决策树所需的时间呈线性增加,但是随机森林所需时间的增长率远大于C4.5决策树。
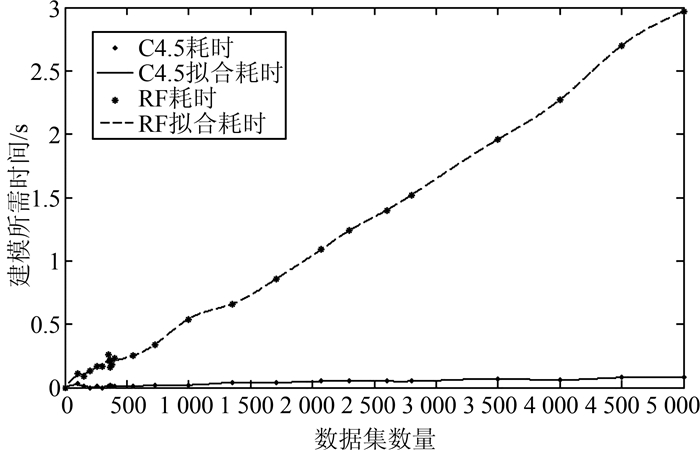 |
| 图 4 对不同数据集建模所需的时间 Figure 4 Modeling Time for Different Data Sets |
3 结束语
在降水的预测中,基于统计的相关分析和回归分析在处理非线性相关特征时有局限性,数据挖掘具备处理这方面问题的能力。本文采用决策树中运用广泛的C4.5决策树、随机森林,把ECMWF的气象数据(地表温度、大气压强、风速、大气可降水量以及露点温度)作为特征属性,对有无降水进行预测。随机森林的平均预测准确度为84.36%,C4.5决策树的平均预测准确度为82.63%,两者都远高于SLIQ的平均预测准确度(75.11%)。但是,随机森林建模所需的时间远大于C4.5决策树所需的时间。所以,对于记录数量很大的数据集来说,在对准确率要求不是很严格的情况下,可以采用C4.5决策树进行预测。
| [1] | 高涛, 谢立安. 近50年来中国极端降水趋势与物理成因研究综述[J]. 地球科学进展, 2014, 29(5): 577–589 DOI: 10.11867/j.issn.1001-8166.2014.05.0577 |
| [2] |
段亚雯, 朱克云, 马柱国, 等. 中国区域1961-2010年降水集中指数(PCI)的变化及月分配特征[C]. 中国大地测量和地球物理学学术大会, 南京, 2014 http://kns.cnki.net/KCMS/detail/detail.aspx?filename=dqxk201406009&dbname=CJFD&dbcode=CJFQ |
| [3] | |
| [4] | 闵晶晶, 孙景荣, 刘还珠, 等. 一种改进的BP算法及在降水预报中的应用[J]. 应用气象学报, 2010, 21(1): 55–62 DOI: 10.11898/1001-7313.20100107 |
| [5] | 刘还珠, 赵声蓉, 陆志善, 等. 国家气象中心气象要素的客观预报——MOS系统[J]. 应用气象学报, 2004, 15(2): 181–191 |
| [6] | 曾晓青, 邵明轩, 王式功, 等. 基于交叉验证技术的KNN方法在降水预报中的试验[J]. 应用气象学报, 2008, 19(4): 471–478 DOI: 10.11898/1001-7313.20080411 |
| [7] | 冯汉中, 陈永义. 处理非线性分类和回归问题的一种新方法(Ⅱ)——支持向量机方法在天气预报中的应用[J]. 应用气象学报, 2004, 15(3): 355–365 |
| [8] | Prasad N, Kumar P, Naidu M M. An Approach to Prediction of Precipitation Using Gini Index in SLIQ Desicion Tree[C]. International Conference on Intelligent Systems Modelling & Simulation, Bangkok, Thailand, 2013 http://ieeexplore.ieee.org/document/6498236/ |
| [9] | Prasad N, Reddy P K, Naidu M M. A Novel Desicion Tree Approach for the Prediction of Precipitation Using Entropy in SLIQ[J].2013 UKSim 15th International Conference on Computer Modelling and Simulation, Cambridge, United Kingdom, 2013 http://ieeexplore.ieee.org/document/6527417/ |
| [10] | Salzberg S L. C4.5: Programs for Machine Learning by J. Ross Quinlan[J]. Machine Learning, 1994, 16(3): 235–240 |
| [11] | 云玉屏, 林克正. C4.5算法在冠状造影数据处理中的应用[J]. 计算机工程与应用, 2008, 44(10): 244–245 DOI: 10.3778/j.issn.1002-8331.2008.10.073 |
 2017, Vol. 42
2017, Vol. 42

