| 不同机载LiDAR点云滤波算法对比分析 |
机载激光雷达(light detection and ranging, LiDAR)技术结合了全球定位系统、激光扫描仪、惯导系统,能够快速高效地获取高精度地面点云数据[1]。目前,该技术已被广泛应用于高压输电线路巡检、水利水电勘测、道路设计、城市规划等领域[2]。机载LiDAR点云数据可以作为数字地面模型(digital terrain model, DTM)的原始数据,是高精度DTM建立的数据保障。对点云中地面点部分数据进行插值等处理步骤后,即可生成DTM。利用机载LiDAR扫描技术可以获取测区的离散点云数据,其中,位于真实地形表面的点云数据被称为地面点,而位于自然植被、树木或人工建筑物表面的点云数据被称为地物点。在利用激光点云数据生成DTM前,需要将地物点从原始数据中全部滤除,该过程被称为点云滤波[3]。
许多学者对不同滤波算法的误差进行了对比,Sithole等[4]开展了一项点云滤波实验,利用8种滤波算法对多组机载点云数据进行滤波处理,并且对比了各组算法的误差,最后得出自适应不规则三角网(triangulated irregular network, TIN)滤波算法的滤波误差最小;Montealegre等[5]对7种滤波算法进行了对比实验,其中包括LAStools工具集的TIN滤波算法和MCC-LiDAR工具的基于多尺度曲率分类的滤波算法(简称多尺度曲率滤波算法),最后得出的结论为MCC-LiDAR滤波得到的整体效果最好,LAStools中TIN滤波算法的精度次之;还有学者提出了新的机载点云滤算法——布料模拟滤波(cloth simulation filtering, CSF)[6]算法。在此基础上,本文从实用角度出发,利用公开数据,对比分析LAStools中的TIN滤波算法、MCC-LiDAR中的多尺度曲率滤波算法和CSF算法,将各算法的滤波结果与参考数据进行比对,对比各算法滤波结果误差的大小,选出一种最适合实际生产的滤波算法。
1 实验数据本文实验数据为国际摄影测量与遥感学会(International Society for Photogrammetry and Remote Sensing, ISPRS)提供的参考点云数据集,该数据集中共有15组点云文件,这些点云数据都具有不同的地形和地物特征,能够充分测试不同滤波算法在不同环境下的滤波效果。同时,这些参考数据都已被人工手动分类,每个点都已被分类为地物点或地面点,因此可以量化地评价各滤波算法的滤波效果。
根据地形差异和坡度的大小,这15组点云数据可以被分成3类[6],结果见表 1。在实验中,分别从每类中选择两组数据进行实验,在第一类数据中选择了数据S31和S51;在第二类数据中选择了数据S11和S22;在第三类数据中选择了数据S52和S53。共选取了6组点云数据进行滤波误差对比实验。
| 表 1 3类点云数据 Tab.1 3 Types of Point Cloud Data |
 |
2 机载点云滤波 2.1 滤波算法
1)渐进三角网滤波算法。该算法由Axelsson[7]提出,其原理是先选取局部区域的最低点作为生成TIN的种子点,然后再利用剩下的点来对三角网格进行迭代加密。计算候选点到所在网格的距离和角度,将满足阈值要求的候选点加入三角网格,使三角网格更加贴近实际地形情况,迭代过程会一直进行,直到没有合适的点加入三角网格为止。
2)多尺度曲率滤波算法。该算法由Evans等[8]提出,是一种基于插值的迭代滤波算法,结合了曲率滤波的优势,并且在插值阶段添加了比例分量。该方法先是采用薄板样条插值(thin plate spline, TSP)方法进行插值,拟合一个地形曲面,然后通过限定曲率阈值,将不满足条件的点标记为地物点,对未分类的点云进行反复迭代,直到原始数据中不存在地物点。TSP方法允许调整点之间的张力,且它的能量函数有合理的物理解释,相对于其他插值方法,该方法能产生更加平滑的曲面。
3) CSF算法。CSF算法由Zhang等[6]提出,在利用其进行滤波处理时,需要利用第三方软件删除原始点云数据中的离群点。其原理是先将原始点云数据进行上下翻转,然后将翻转后的点云数据和用户模拟出来的布料节点投影到同一水平面上,在点云数据中找到布料中每个节点对应的点,并记录下该对应点在投影前的高度,记为IH。在每次迭代过程中,比较布料节点的当前高度和IH的大小,重复迭代,直到达到最大迭代次数或者节点的高程变化足够小,迭代终止。最后计算激光点云到布料节点之间的距离,当该距离大于特定阈值时,该点就被标记为非地面点,反之则被标记为地面点。
CSF算法有5个可以调节的参数:①类别阈值是用来区别激光点是地面点还是地物点的依据,通常设置为0.5 m,能够满足大部分的分类需求;②格网分辨率是指相邻布料节点之间的距离;③时间间隔用来控制重力对粒子位移量的大小;④迭代次数,通常设置为500;⑤布料硬度用来控制布料的松紧程度。实际滤波过程中通常只有格网分辨率和布料硬度两个参数需要修改。
2.2 误差评定标准在定性比较部分,将各滤波结果生成的DTM和参考数据生成的DTM作差,形成DTM差异模型。观察DTM差异模型中误差的分布,可以判断出各滤波算法对实验区域不同地形的适应情况。在定量比较部分,本文计算了滤波算法常用的评价指标一类误差(ET1)、二类误差(ET2)和总误差(ET),对各组滤波结果误差值的大小进行具体比较。其中,一类误差指的是地面点被错误划分成为地物点的比例;二类误差指的是地物点被错误划分为地面点的比例;总误差为错误划分的点占所有点的比例。误差的具体计算公式[9]如下:
| $ \left\{\begin{array}{l} E_{T 1}=E_{O} / P_{G} \\ E_{T 2}=E_{C} / P_{O} \\ E_{T}=\left(E_{O}+E_{C}\right) /\left(P_{G}+P_{O}\right) \end{array}\right. $ | (1) |
式中,EO为地面点被分类为地物点的点数;EC为地物点被分类为地面点的点数;PG为参考数据中地面点的总点数;PO为参考数据中地物点的总点数。
本文所有滤波实验都是在同一台电脑上进行的,中央处理器为Intel(R) Core(TM) i7-7700(3.60 GHz),内存8 GB,装配有64位Windows 10操作系统。本文利用不同滤波方法对6组点云数据进行滤波处理,对于不同的实验数据,每种方法对应的处理时间比较接近。以点数最多的数据S11为例,CSF算法、渐进三角网滤波算法和多尺度曲率滤波算法的处理时间分别为3.3 s、0.237 s、5.27 s。
3 实验结果及分析 3.1 DTM差异模型分析对比DTM差异模型可以得到滤波结果中一类误差和二类误差的分布情况,通过颜色的深浅还能判断出高程差异的大小。从6组实验数据中挑选出3组数据(S51、S22、S53)进行DTM差异分析。图 1为3组数据的DTM差异模型图。图 1中,蓝色色块表示实际地面存在点云,而滤波算法将其滤除的区域,代表了一类误差的分布区域;红色色块为滤波结果中存在点云,而实际参考地面中不存在的区域,代表了二类误差的分布区域。
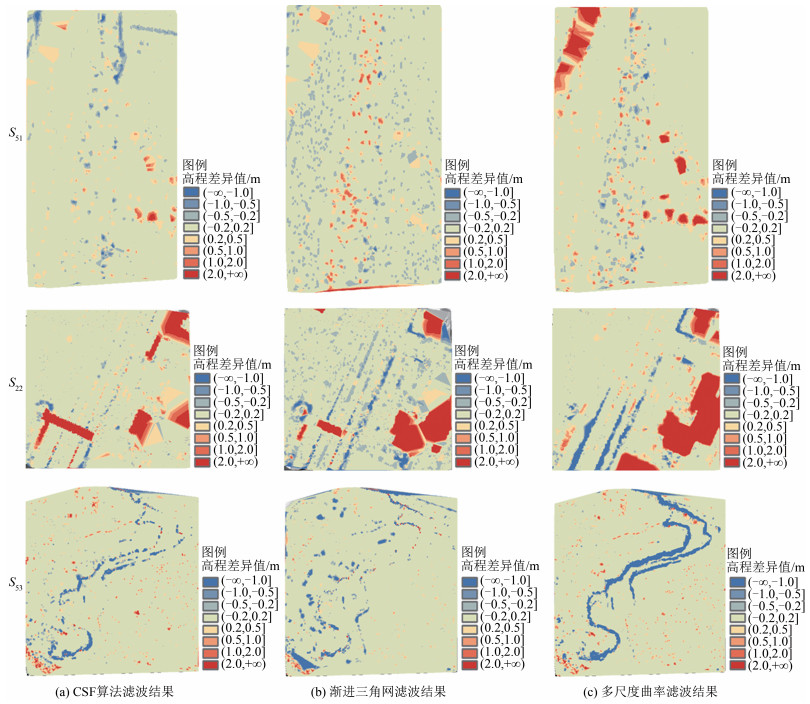 |
| 图 1 3组数据的DTM差异模型 Fig.1 DTM Difference Model for Three Data Sets |
从图 1中S51的DTM差异模型可以看出,3种滤波算法所得到的滤波误差差异较大,CSF算法滤波后的误差相对集中在实验区域中部,该区域植被较多,且地形为斜坡。S51进行CSF算法滤波后,误差以蓝色为主,说明该算法成功将植被从斜坡上滤除,但部分地面点被误分成了地物点;DTM差异模型中还零星存在一些红色色块,大多位于低矮房屋附近,滤波算法没有将其正确滤除。S51渐进三角网滤波结果的误差较为分散,其中红色色块主要集中在植被集中的斜坡地带,建筑物大多都被正确滤除;蓝色色块比较分散,且都较小,说明整个实验区域都存在地面点被误分成地物点的情况。S51的多尺度曲率滤波算法DTM差异模型中,较多地物点被误分成地面点,这些地物点主要集中在房屋边缘和河道两侧;而在中间斜坡地带,地面点和地物点被误分的情况都存在。
在S22的DTM差异模型中,CSF算法没有正确滤除与地面相连的地物(实验区域中的两座桥梁),并且也有部分实验区域边缘的建筑物没有被正确滤除;渐进三角网滤波算法正确滤除了一座点云数量较少的桥,对另一座桥没有正确滤除,也有较多的建筑物点云数据没有被正确分类;多尺度曲率滤波算法正确滤除了两座桥梁,但也有较多建筑物数据没有被滤除。
S53为矿区地形数据,其地形高差大,且地物点分布零散。其CSF算法和多尺度曲率滤波算法的结果中分布了许多红色色块,这表明这两种算法都没有将零散的地物点滤除,而且滤波结果中存在蓝色条带,这些条带位于矿区地形台阶的边缘,滤波算法将这部分地面点误分成了地物点。而S53的渐进三角网滤波结果较好,地物点大都被滤除,台阶地形的边缘也没有出现成片地面点被滤除的情况,但其倾向于将地物点周边的地面点滤除,因此结果中还存在较多的蓝色色块。
通过观察各滤波结果生成的DTM差异模型,能够大致查看出两类误差的分布情况及各类误差的相对大小,但要客观评价各滤波算法的效果还需要对滤波结果的误差进行量化比较。
3.2 误差定量分析表 2展示的是各滤波结果一类误差、二类误差、总误差的计算结果,可以看出,在各组数据的滤波结果中,CSF算法的一类误差均最小,在平坦地形数据S31和S51中,其二类误差也特别小。对于存在陡坡或断裂地形的数据S52和S53, CSF算法的二类误差值较大,这说明在这两组数据中有较大比例的地物点数据被误分成了地面点,但由于总的地物点数量并不多,因此二类误差对总误差的值影响不大。而渐进三角网滤波算法在S52和S53中的二类误差值相对较小,这说明其地物点被误分为地面点的比例相对较低。在平坦地形数据S31中,多尺度曲率滤波算法的一类误差值达到了10.9%,这说明有较多地面点数据被误分成了地物点数据。
| 表 2 误差计算结果 Tab.2 Calculation Results of Errors |
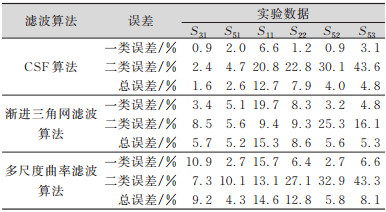 |
渐进三角网滤波算法在S11、S22、S52、S53中的二类误差都取得了最小值,即原始数据中地物点被误分成地面点的比例低,但是一类误差的值都较大,表明有较多地面点被误分成了地物点,这种误差分布规律说明,该算法为了正确分离地物点,是以错误分离地面点为代价的。
图 2是所有滤波结果的总误差直方图,可以看出,CSF算法在全部实验数据中的总误差值最小。对于平坦地形数据S31和S51,总误差最小值和次最小值的差值为4.1%、1.7%,但在地形起伏较大的S22、S52和S53中,总误差的最小值和次最小值之差分别为0.7%、1.6%、0.5%。差值的减小说明,针对平坦地形数据,CSF算法的处理优势较为明显,但对于地形起伏较大的数据,CSF算法和渐进三角网滤波算法的滤波效果接近。
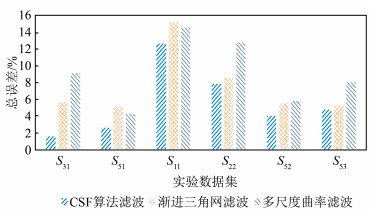 |
| 图 2 各实验数据总误差 Fig.2 Total Error of Each Experimental Data |
从图 3(a)中可以看出,3种滤波算法的一类误差都是在S11数据中取得最大值,S11数据总体地形为斜坡,斜坡上密集分布了许多植被和建筑物。而对于地物分布较为稀疏的S52和S51, 3种滤波算法的误差值均较小。通过以上分析可以看出,一类误差值的大小与实验区域中地物点的密集程度相关。
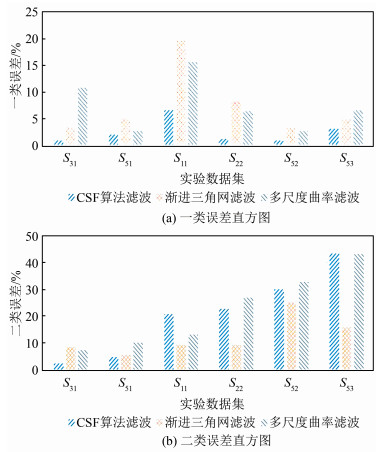 |
| 图 3 实验数据的一类误差、二类误差 Fig.3 Type Ⅰ and Type Ⅱ Errors of Experimental Data |
图 3(b)中,S31和S51属于实验数据中的第一类(平坦地形数据);而S11和S22属于第二类(存在斜坡或阶梯地形的数据);S52和S53为第三类(存在陡坡地形的数据)。从直方图的高低关系可以看出,随着地形坡度的增大,滤波结果的二类误差增大。
3.3 实验结果讨论通过以上对实验结果的分析,可以从定性和定量两方面对3种机载点云滤波算法有一个具体认识。CSF算法在6组数据的滤波结果中,总误差值都最小,且算法需要设置的有效参数少、设置简单,最适用于处理城镇平坦地形数据;但是在复杂地形条件下,其滤波误差会增大,对实验区域边缘的建筑物和与地面相连地物点的滤除效果不佳。渐进三角网滤波算法参数设置较为简单,对于矿区阶梯地形地面点保留效果较好,滤波速度最快;但是该算法在过滤过程中容易将地面点滤除,且进行参数设置时,需要提前知道地表地物尺寸的大小。多尺度曲率滤波算法的处理时间最长,能够滤除与地面相连的桥梁点云数据;但是实际操作时选择合适的参数较困难,需要测试的次数最多,在对平坦地形的建筑物进行滤波时,容易保留建筑物点云数据。
4 结束语机载LiDAR点云滤波是生产DTM的重要步骤,本文以ISPRS提供的专门用来对比滤波算法的参考数据集为实验数据,对CSF算法、渐进三角网滤波算法和多尺度曲率滤波算法进行对比实验,据滤波结果的一类误差、二类误差和总误差来评价不同滤波算法的滤波效果。多组实验结果表明,CSF算法在6组测试数据中的总误差值均最小。在地形坡度较大的S52和S53数据中,渐进三角网滤波算法的总误差值和CSF算法的总误差值接近。多尺度曲率滤波算法虽然也能滤除大部分地物点,但对于地形边界、建筑物周边的点不能正确区分,导致其结果的总误差值较大。对各组测试数据的滤波结果进行对比分析,发现CSF算法是机载激光点云数据的最佳滤波算法,尤其适用于处理地形平坦、地物类别主要为建筑物的城镇点云数据。对于地形坡度较大的山体类型数据,渐进三角网滤波算法同样是一个很好的选择,其速度更快,滤波效率更高。
| [1] |
基于多分辨率方向预测的LiDAR点云滤波方法[J]. 武汉大学学报·信息科学版, 2007, 32(11): 1 011-1 015. |
| [2] |
基于LiDAR数据的等高线树构建研究[J]. 测绘地理信息, 2015, 40(5): 21-24. |
| [3] |
曹红新. 机载LIDAR数据滤波方法研究[D]. 成都: 西南交通大学, 2011
|
| [4] |
Sithole G, Vosselman G. ISPRS Comparison of Filters[R]. Delft: Delft University of Technology, 2003
|
| [5] |
Montealegre A L, Lamelas M T, de la Riva J. A Comparison of Open-Source LiDAR Filtering Algorithms in a Mediterranean Forest Environment[J]. IEEE Journal of Selected Topics in Applied Earth Observations and Remote Sensing, 2015, 8(8): 4 072-4 085. DOI:10.1109/JSTARS.2015.2436974 |
| [6] |
Zhang W M, Qi J B, Wan P, et al. An Easy-to-Use Airborne LiDAR Data Filtering Method Based on Cloth Simulation[J]. Remote Sensing, 2016, 8(6). DOI:10.3390/rs8060501 |
| [7] |
Axelsson P. DEM Generation from Laser Scanner Data Using Adaptive TIN Models[J]. International Archives of Photogrammetry and Remote Sensing, 2000, 23(B4): 110-117. |
| [8] |
Evans J S, Hudak A T. A Multiscale Curvature Algorithm for Classifying Discrete Return LiDAR in Forested Environments[J]. IEEE Transactions on Geoscience and Remote Sensing, 2007, 45(4): 1 029-1 038. DOI:10.1109/TGRS.2006.890412 |
| [9] |
Serifoglu Y C, Yilmaz V, Güngör O. Investigating the Performances of Commercial and Non-Commercial Software for Ground Filtering of UAV-Based Point Clouds[J]. International Journal of Remote Sensing, 2018, 39(15/16): 5 016-5 042. |
 2021, Vol. 46
2021, Vol. 46

