| 马尔科夫链改进的ARIMA-BP神经网络模型研究 |
2. 精密工程与工业测量国家测绘地理信息局重点实验室,湖北 武汉,430079
2. Key Laboratory of Precise Engineering and Industry Surveying of National Administration of Surveying,Mapping and Geoinformation,Wuhan 430079,China
在工程设计施工中,地基沉降监测至关重要。对地基沉降的控制不准确会导致建筑物的功能失效,甚至造成坍塌等严重事故。由于地基沉降规律受到多种因素的制约[1],沉降过程既包含线性规律,又包含非线性规律。本文采用的自回归滑动平均(auto regressive integrated moving average,ARIMA)和反向传播(back propogation,BP)神经网络组合模型中,ARIMA模型能够合理地描述历史数据的线性关系,BP神经网络能够模拟数据的非线性规律。马尔科夫链(Markov Chain)[2]对于受多种因素影响的序列预测具有一定的优越性,适合描述随机波动性较大的过程。本文结合某地基沉降数据,利用ARIMA-BP神经网络组合模型进行预测,并根据马尔科夫理论对预测结果进行改进,结果表明,预测精度有了一定的提高。
1 改进的ARIMA-BP神经网络预测模型 1.1 时间序列分析法时间序列分析法是利用数据的自相关性建立相对最优的模型来分析客观现象的动态特征。其主要模型为ARIMA模型[3]。如果一个时间序列{Yt}的d次差分Wt=∇dYt是一个平稳的ARMA(auto regressive moving average)过程,则称{Yt}为自回归滑动平均求和模型,记为ARIMA(p,d,q),其中,d为差分次数。ARIMA模型的通用表达式为:
| $\begin{align} & {{W}_{t}}={{Y}_{t}}-{{Y}_{t-1}}={{\varphi }_{1}}\left( {{Y}_{t-1}}-{{Y}_{t-2}} \right)+{{\varphi }_{2}}\left( {{Y}_{t-2}}-{{Y}_{t-3}} \right)+\ldots + \\ & {{\varphi }_{p}}\left( {{Y}_{t-p}}-{{Y}_{t-p-1}} \right)+{{e}_{t}}-{{\theta }_{1}}{{e}_{t-1}}-{{\theta }_{2}}{{e}_{t-2}}-\ldots -{{\theta }_{q}}{{e}_{t-q}}= \\ & {{\varphi }_{1}}{{W}_{t-1}}+{{\varphi }_{2}}{{W}_{t-2}}+\ldots +{{\varphi }_{p}}{{W}_{t-p}}+{{e}_{t}}- \\ & {{\theta }_{1}}{{e}_{t-1}}-{{\theta }_{2}}{{e}_{t-2}}-\ldots -{{\theta }_{q}}{{e}_{t-q}} \\ \end{align}$ | (1) |
式中,φ1,φ2,…,φp是自回归系数,p是自回归阶次;θ1,θ2,…,θq是滑动平均系数,q是滑动平均阶次;et是白噪声序列。该模型通常表示为ARIMA(p ,d,q)。
ARIMA模型的建模及预测过程分为以下4个步骤[4]。
1) 模型识别。检验序列的平稳性,对非平稳序列进行差分处理,再对模型定阶。
2) 参数估计。对模型φ、θ等系数进行估计,通常采用最小二乘估计、极大似然估计等。
3) 模型诊断。进行模型适用性检验,分析拟合模型的残差。
4) 预测。用所得时间序列模型进行预测。
1.2 BP神经网络法BP神经网络是人工神经网络中使用最多的一种网络。该网络由输入层、隐含层和输出层[5] 3层组成,如图 1所示。3层的节点个数分别记为N、Q、M。
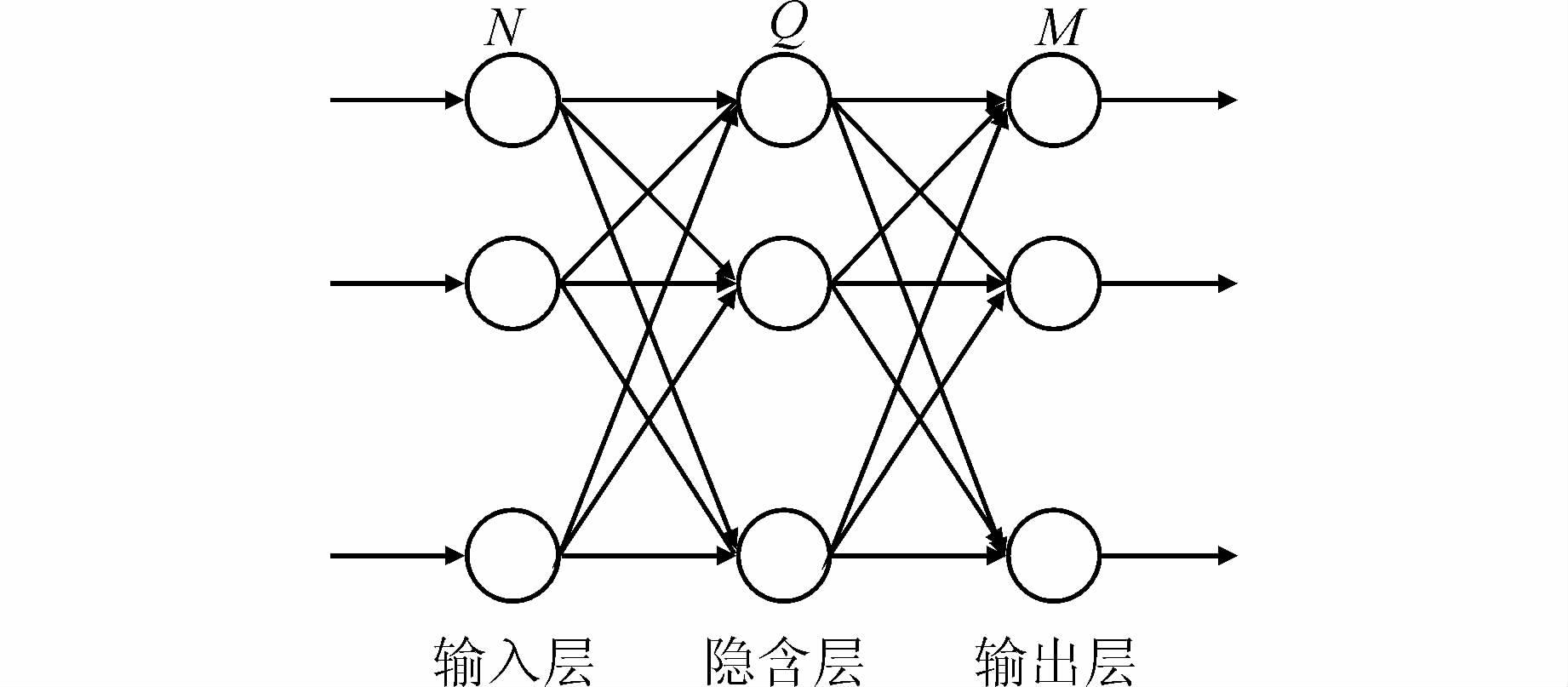 |
| 图 1 BP神经网络结构 Figure 1 Structure of BP Neural Network |
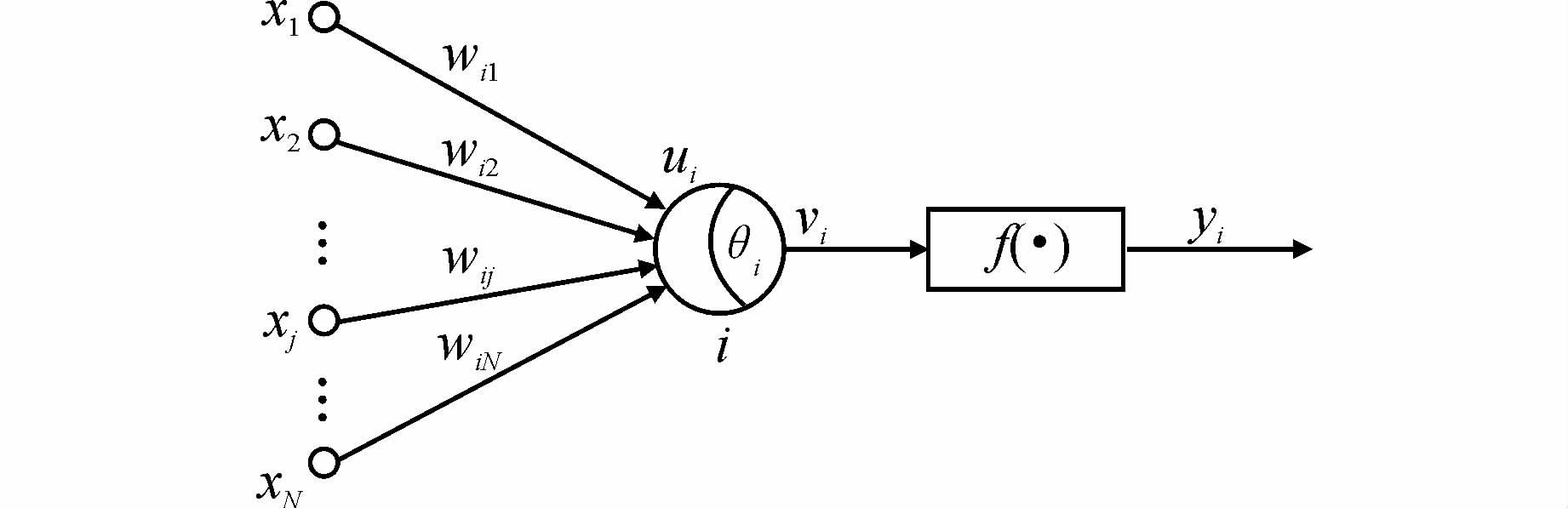 |
| 图 2 神经元模型 Figure 2 Neuron Model |
图 2中,xj(j=1,2,…,N)为神经元j的输入信息;wij为网络的连接权重;ui是输入信号和连接权值内积的结果,是神经元i的输入信号,经过阈值θi的调整,作为激活函数的自变量,得到神经元的输出yi。BP神经网络的算法实现流程如下。
1) 随机赋值所有的权值,给定阈值初始值。
2) 确定输入信号和期望输出。
3) 计算实际输出yi=f(∑wijxi),神经元的激活函数常采用Sigmoid[7]函数:
| $f\left( x \right)={{(1+{{e}^{-ax}})}^{-1}}$ | (2) |
式中,a为常数。
4) 调整权值,从输出节点开始返回到隐含层,权值修正公式为:
| $\begin{align} & {{w}_{ij}}\left( t+1 \right)={{w}_{ij}}\left( t \right)+\eta ~{{\delta }_{j}}{{y}_{i}}+ \\ & b\left[ {{w}_{ij}}\left( t \right)-{{w}_{ij}}\left( t-1 \right) \right] \\ \end{align}$ | (3) |
式中,η为大于0的增益;δj为节点j的误差;b为动量因子,0<b <1。
5) 重复步骤2)~4),直到达到训练要求为止。
1.3 ARIMA-BP神经网络模型ARIMA-BP神经网络模型进行预测有以下几个步骤。
1) 建立合适的ARIMA模型。对样本进行预测,并计算得到拟合误差序列。
2) 对1)中得到的拟合误差序列进行BP神经网络建模,并预测。
3) 用2)中得到的拟合误差的预测值对1)中的ARIMA预测值进行修正,得到ARIMA-BP神经网络模型的预测值。
1.4 利用马尔科夫过程改进ARIMA-BP模型预测结果马尔科夫过程是具有无后效性的随机过程[8]。无后效性是指当序列在某时刻处于已知状态时,序列在该时刻之后的所有时刻状态的概率特性只与该时刻的状态有关,而与序列在该时刻以前的状态无关。当马尔科夫过程的时间离散且状态离散时,该过程称为马尔科夫链。
根据马尔科夫链将数据序列划分为多个不同状态,分别用E1,E2,E3,…,Em来表示。马尔科夫链从状态Ei经过k步转移到Ej的概率称为转移概率Pij(k)为:
| $P_{ij}^{\left( k \right)}=\frac{m_{ij}^{\left( k \right)}}{{{M}_{i}}}$ | (4) |
式中,Mi为状态Ei在过程中出现的次数;mij(k)为状态Ei经过k步转移到Ej的次数,得到1步状态转移概率矩阵为:
| ${{P}^{(1)}}=\left[ \begin{matrix} P_{11}^{\left( 1 \right)} & \cdots & P_{1m}^{\left( 1 \right)} \\ \vdots & {} & \vdots \\ P_{1m}^{\left( 1 \right)} & \cdots & P_{mm}^{\left( 1 \right)} \\ \end{matrix} \right]$ | (5) |
根据切普曼-柯尔莫哥洛夫方程[9],可知k步的状态转移概率矩阵为:
| ${{P}^{(k)}}={{\left( {{P}^{(1)}} \right)}^{k}}$ | (6) |
若某状态Ei的初始状态向量为P0,则经过k步状态转移后的状态向量为:
| ${{P}_{k}}={{P}_{0}}\times {{P}^{(k)}}$ | (7) |
利用马尔科夫过程改进ARIMA-BP预测模型,其步骤如下。
1) 建立ARIMA-BP神经网络模型。
2) 用黄金分割法[10]将预测结果序列的误差分为若干个状态区间,并反归一化到原状态区间。
3) 根据每期误差落入不同的区间结果计算状态转移概率矩阵,并计算未来多步的状态转移概率矩阵。
4) 计算未来n个时间间隔的状态区间,根据1)中的原状态区间得到区间分界值。
5) 选择状态分布概率最大的区间,取该区间的均值作为改进的预测值。
2 实验与分析采用某地基历史45期沉降数据,取前30期作为样本数据,后15期为测试对比数据进行实验。历史实测数据如表 1所示。
| 表 1 地基实测沉降数据 Table 1 Measured Foundation Settlement Data |
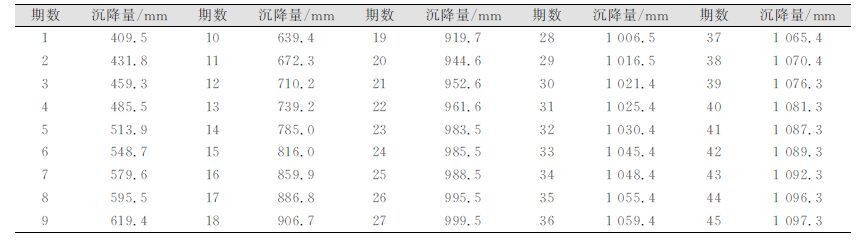 |
2.1 ARIMA模型预测
原始数据为非平稳序列,需要进行差分处理。图 3为沉降数据经二次差分后的时间序列图。由图 3可知,经二次差分后序列大致为平稳状态,确定ARIMA模型差分次数d=2。
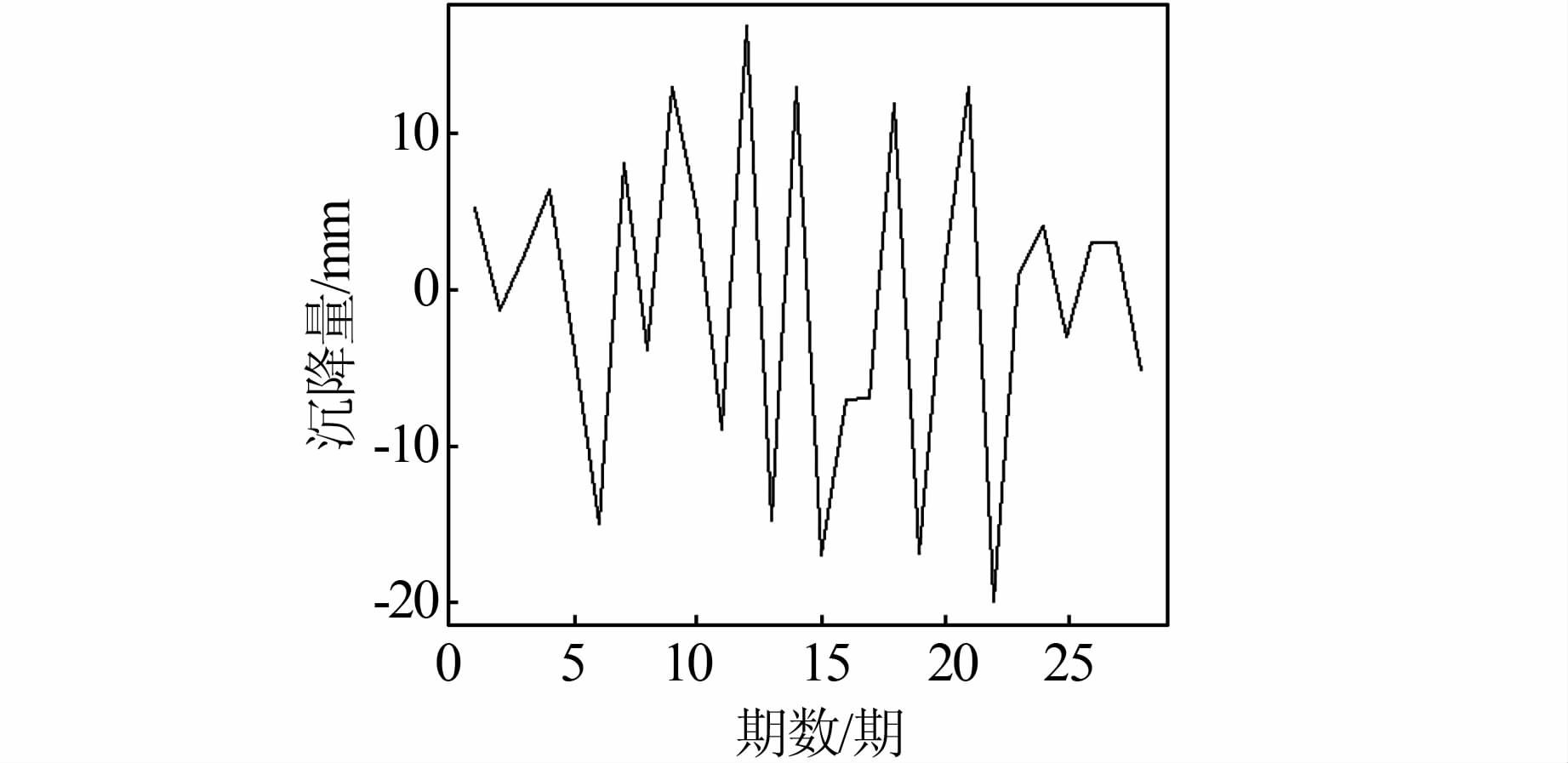 |
| 图 3 沉降量经二次差分后的时间序列图 Figure 3 Time-Series of Twi-Differential Settlement Data |
模型定阶先用自相关函数(autocorrelation function,ACF)和偏自相关函数(partial autocorrelation function,PACF)进行初步判断,如图 4所示。自相关和偏自相关函数的特征如表 2所示。
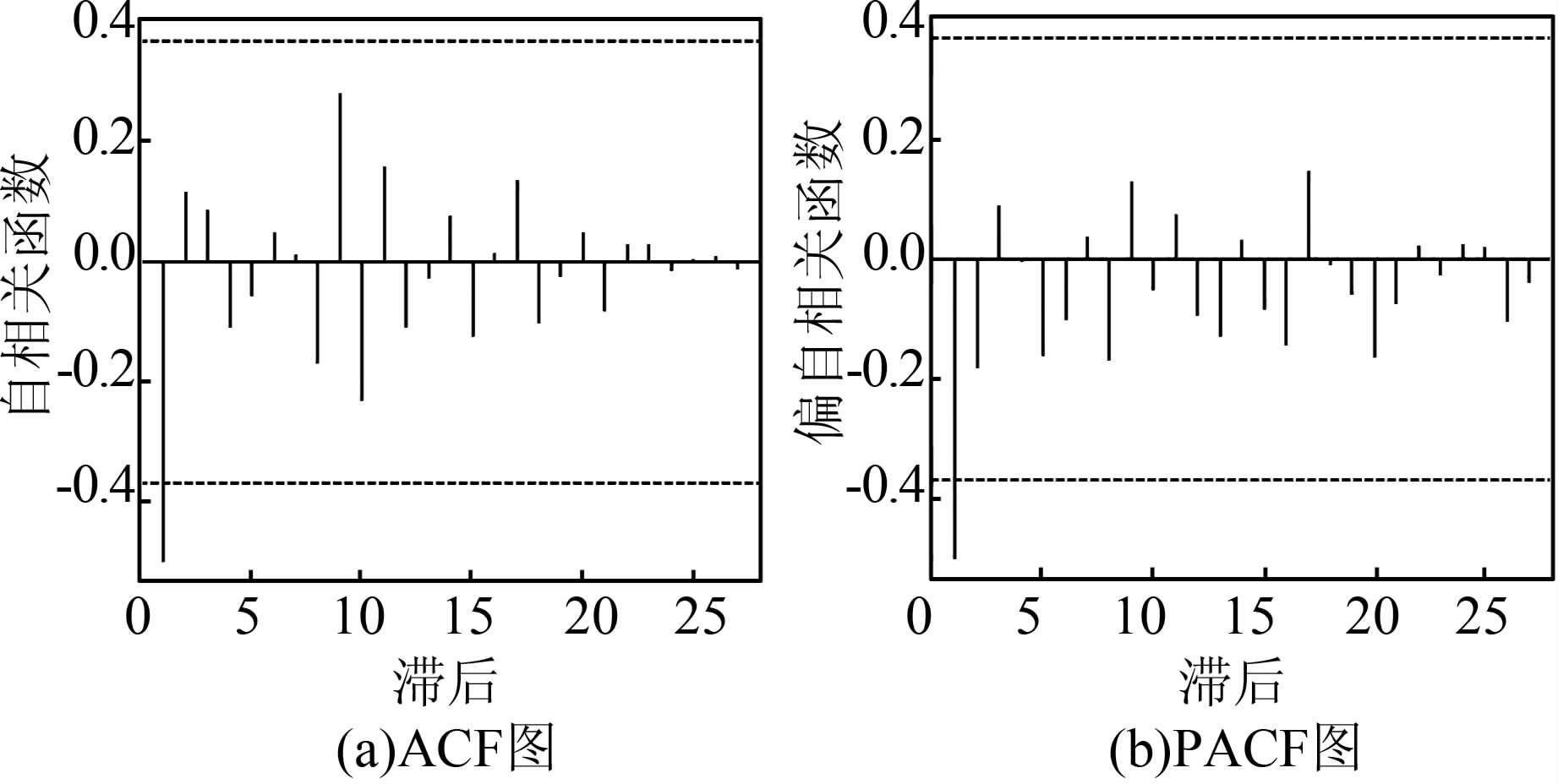 |
| 图 4 自相关和偏自相关函数图 Figure 4 ACF and PACF Charts |
| 表 2 ARMA模型ACF和PACF的一般特征 Table 2 General Features of ACF and PACF in ARMA Model |
 |
由图 4、表 2可以看出,ACF图和PACF图都是拖尾的,且都在滞后1阶后显著减小,初步判定差分后序列模型为ARMA(1,1)模型。再用扩展自相关函数(extended autocorrelation function,EACF)图进一步判断,输出扩展自相关函数图,如图 5所示。图 5表明模型ARIMA(1,2,1)基本符合原始序列。
 |
| 图 5 扩展自相关函数图 Figure 5 EACF Chart |
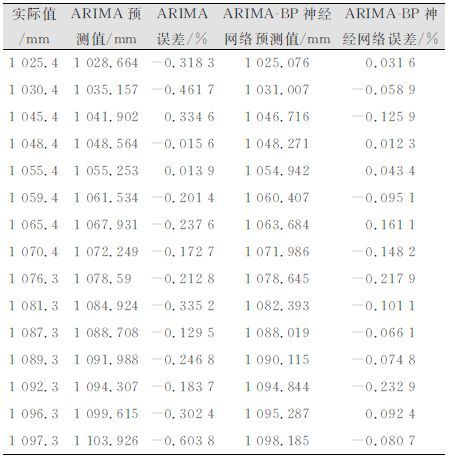
在利用极大似然估计法进行参数估计后,进行模型诊断,分析残差的正态性和自相关性并进行Ljung-Box检验,满足条件后根据 ARIMA(1,2,1)模型对原始序列进行未来15期的预测。预测结果及其误差如表 3所示。
2.2 ARIMA-BP神经网络模型预测采用滚动式[11]的预测方法来预测其误差。以1~5期预测误差为网络输入,第6期为网络输出;2~6期预测误差为网络输入,第7期为网络输出,以此类推到24~29期网络输入,30期为网络输出,组成样本进行训练。经实验,隐含层神经元个数为15时最优。权值训练算法采用L-M[12]优化算法,训练次数设为500,训练精度为10-5,学习速率为0.01。利用MATLAB工具进行预测,网络经过24次训练到达最小误差。
对误差序列进行15步预测,结果与ARIMA模型预测值线性相加得到ARIMA-BP神经网络模型预测值,其结果与相对误差如表 3所示。可以看出,ARIMA-BP神经网络模型在一定程度上提高了预测精度。
| 表 3 ARIMA和ARIMA-BP神经网络模型预测值及误差 Table 3 Forecast and Error Values of ARIMA Model and ARIMA-BP Neural Network Model |
 |
2.3 马尔科夫链改进ARIMA-BP模型预测
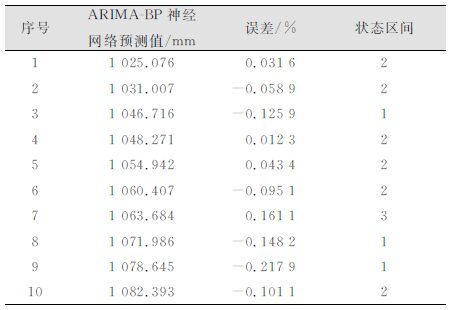
在ARIMA-BP神经网络模型的基础上,取ARIMA-BP神经网络模型预测值的前10期作为马尔科夫改进样本。其平均误差为-0.049 9%,归一化后为0.443 4。利用黄金分割法得到3个状态区间为[0,0.274 0],(0.274 0,0.717 4],(0.717 4,1]。将其反归一化得到该10期误差的状态区间为[-0.217 9,-0.114 1],(-0.114 1,0.054 0],(0.054 0,0.161 1]。依次将这3个区间称为状态区间1、2、3。前10期误差的状态区间分布如表 4所示。
由表 4得1步状态转移概率矩阵为:
| 表 4 误差状态区间分布 Table 4 Distribution of Error State Interval |
 |
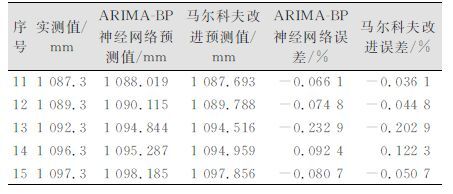
| 表 5 马尔科夫链改进的预测值及误差 Table 5 Forecast and Error Values Improved by Markov Chain |
 |
| 表 6 两种模型的预测精度比较 Table 6 Comparison of Forecast Accuracy of Two Models |
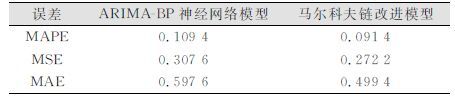 |
由表 5、表 6可以看出,ARIMA-BP模型预测值经马尔科夫链改进后精度有一定的提高。
3 结束语以上对地基沉降预测模型的研究结果表明,ARIMA-BP神经网络模型准确描述了序列的线性部分和非线性部分,比单一ARIMA模型预测精度高。利用马尔科夫链改进ARIMA-BP神经网络模型预测值,其预测结果精度更高,这种改进方法可以有效运用于沉降预测中。由于地基沉降机理的复杂性,沉降量的预测难以达到严格准确,在实际项目中,应结合实际情况进一步检验预测结果。
| [1] |
李磊.地基沉降预测方法分析[D]. 杭州:浙江大学,2004 Li Lei.A Research on the Methods for Predicting Foundation Settlement[D].Hangzhou:Zhejiang University,2004 http://cdmd.cnki.com.cn/Article/CDMD-10335-2004075885.htm |
| [2] |
龙浩, 高睿, 孔德新, 等. 基于BP神经网络-马尔科夫链模型的隧道围岩位移预测[J].
长江科学院院报,2013,30(3) : 40–43.
Long Hao, Gao Rui, Kong Dexin, et al. Forecast of Tunnel’s Surrounding Rock Displacement by BP Neural Network and Markov Chain[J]. Journal of Yangtze River Scientific Research Institute,2013,30(3) : 40–43. |
| [3] | Cryer J D, Chan K S. Time Series Analysis with Applications in R[M]. 2nd ed. Beijing: China Machine Press, 2011 . |
| [4] |
陈艳华, 邹进贵, 李波, 等. ARIMA乘积季节模型在大坝位移监测中的应用[J].
测绘地理信息,2014,39(2) : 35–38.
Chen Yanhua, Zou Jingui, Li Bo, et al. Application of Multiplicative Seasonal ARIMA Model in Dam Displacement Monitoring[J]. Journal of Geomatics,2014,39(2) : 35–38. |
| [5] |
李友坤.BP神经网络的研究分析及改进应用[D].淮南:安徽理工大学,2012 Li Youkun.Analysis and Improvement Applications of BP Neural Network[D].Huainan: Anhui University of Science and Technology,2012 http://cdmd.cnki.com.cn/Article/CDMD-10361-1012421305.htm |
| [6] |
李聪.基于BP神经网络的股票指数期贷价格预测[D].青岛:青岛大学,2012 Li Cong.Forecast of Stock Index Futures’Prices Based on BP Neural Network[D].Qingdao:Qingdao University,2012 http://epub.cnki.net/kns/detail/detail.aspx?QueryID=60&CurRec=1&recid=&FileName=1012346347.nh&DbName=CMFD201301&DbCode=CMFD&pr= |
| [7] |
杨杰, 吴中如, 顾冲时, 等. 大坝变形监测的BP网络模型与预报研究[J].
西安理工大学学报,2001,17(1) : 25–29.
Yang Jie, Wu Zhongru, Gu Chongshi, et al. Dam Deformation Monitoring Model and Forecast Based on BP Algorithm of Artificial Neural Networks[J]. Journal of Xi’an University of Technology,2001,17(1) : 25–29. |
| [8] |
牛东晓, 关哲, 任峰, 等. 基于马尔科夫过程的电力企业市场竞争预测[J].
华北电力大学学报,2004,31(1) : 66–68.
Niu Dongxiao, Guan Zhe, Ren Feng, et al. Market Percentage Prediction Based on Markov Chain in Electric Power Enterprise Competition[J]. Journal of North China Electric Power University,2004,31(1) : 66–68. |
| [9] |
王义民, 于兴杰, 畅建霞, 等. 基于BP神经网络马尔科夫模型的径流量预测[J].
武汉大学学报·工学版,2008,41(5) : 14–17.
Wang Yimin, Yu Xingjie, Chang Jianxia, et al. Prediction of Runoff Based on BP Neural Network and Markov Model[J]. Engineering Journal of Wuhan University,2008,41(5) : 14–17. |
| [10] |
林已杰.一种基于马尔科夫和BP神经网络的软件衰退预测方法研究[D].重庆:西南大学,2010 Lin Yijie.A Research of Software Aging Forecasting Method Based on Markov and Neural Network[D].Chongqing:Xinan University,2010 http://epub.cnki.net/kns/detail/detail.aspx?QueryID=68&CurRec=1&recid=&FileName=2010095132.nh&DbName=CMFD2011&DbCode=CMFD&pr= |
| [11] |
雷可为, 陈瑛. 基于BP神经网络和ARIMA组合模型的中国入境游客量预测[J].
旅游学刊,2007,(4) : 20–25.
Lei Kewei, Chen Ying. Forecast of Inbound Tourists in China Based on the Combination of BP Neural Network and ARIMA Model[J]. Tourism Tribune,2007,(4) : 20–25. |
| [12] |
李炯城, 黄汉雄. 神经网络中LMBP算法收敛速度改进的研究[J].
计算机工程与用,2006,(16) : 46–50.
Li Jiongcheng, Huang Hanxiong. Research on Improvement of Convergence Speed of LMBP Algorithm in Neural Network[J]. Computer Engineering and Application,2006,(16) : 46–50. |
 2016, Vol. 41
2016, Vol. 41

