| 地铁自动化监测精度的研究 |
在中国东南沿海,城市建设较为发达,许多城市建设地铁并投入运营。部分城市的地铁工程涉及沿海或沿江的漫滩区域,这些区域地层多为软土、沙质土,地质条件复杂。随城市发展需要,有些建设项目邻近地铁站或地铁线路,这些项目基坑降水等施工会引起地铁隧道周围地下水位的变化和应力场的变化,导致地铁线路周围土体产生变形,造成地铁地下车站、地铁隧道结构的形变,致使地铁正常结构被破坏,地铁运行面临巨大的安全风险[1, 2]。地铁建设拉动了沿线的经济发展,在地铁保护区范围内的项目投入建设,都需开展地铁保护区监测工作。地铁地下车站与隧道周边外侧50 m范围内为地铁保护区。开展地铁保护区智能化监测研究,连续、长期地进行监测,及时发现和预报险情,在保障地铁工程安全及地铁安全运行具有重大意义[3]。
1 监测方法地铁保护区监测主要包括垂直位移监测(沉降监测)、水平位移监测、收敛监测3种。变形监测主要采用水准仪、全站仪、位移计等设备。目前国内对运营地铁的高精度的实时监控方法研究偏少,水平位移监测一般采用全站仪观测,沉降监测一般采用水准仪观测,收敛监测一般采用位移计或坐标反算的方法[4, 5]。测量方法主要为人工测量与高精度全站仪自动化观测为主。人工测量的方法,自动化程度低,劳动强度大且会与地铁的正常运营相互干扰,工作效率低,后期数据处理工作量非常大。高精度全站仪自动化观测,其观测长度也受到限制。随着地铁工程实时化的监测要求,自动化、智能化监测是今后地铁安全监测的主要发展方向。
1.1 人工辅助监测在地铁保护区监测过程中,自动化、智能化监测是发展方向,但有一定的局限性[6, 7]。如垂直自动化位移测量没有几何水准测量的精度高,管片裂缝自动化观测较难实现等。因此,一般地铁保护区监测采用自动化监测为主,人工监测为辅的方式进行。
1) 人工垂直位移监测。采用1985国家高程基准或工程高程系统,在地铁站附近布设3个稳定的工作基点,定期与长期运营监测深桩点进行联测,工作基点应建在基岩或持力层上,监测时采用往返观测。基本水准网观测按照《国家一、二等水准测量规范》要求执行[8]。各监测点高程初始值在监测工程前施测并计算,为保证施测精度与稳定性,应测量3次,在限差内取3次平均值作为各监测点的高程初始值。某监测点本次沉降量为本次高程与前次高程的差值, 累计沉降量为本次高程与初始高程的差值。
2) 隧道水平收敛监测。在工程开挖施工过程中,由于管片周围土压力的变化,可能导致隧道圆形管片收敛变形,因此需要在施工过程中对其进行收敛监测,监测点示意图如图 1所示。
 |
| 图 1 收敛监测点布置图 Fig.1 Rotation of Convergence Monitoring Points |
管片收敛监测采用手持测距仪或经计量合格的钢尺进行测量。测量前按设计要求的丈量密度在管片中部喷漆标识,手持式激光测距仪或钢尺直接丈量收敛测线的长度,以此计算收敛变化值。复测值与初测值之差即为管径变形值。计算公式为:
| $ {h_i} = {D_i} - {D_0} $ | (1) |
式中,hi为本次变化量; Di为本次收敛值; D0为初始收敛值,即hi为负,表示隧道收敛,hi为正,表示隧道扩散。
3) 管片裂缝监测。当管片出现裂缝时,将及时对管片裂缝进行调查,并拍照存档,拍照时垂直裂缝放置钢圈尺。采用智能裂缝测宽仪进行裂缝观测,该仪器可自动判读裂缝宽度、拍摄裂缝照片,实时读数且精度优于0.01 mm,测试范围可达到0~8 mm。施工开始前各方对隧道现状予以确认,在日常监测过程中发现新增的渗漏、裂缝,或原有渗漏、裂缝情况有明显增加时,及时上报并通知相关单位分析原因,排除隐患,并做好拍照存档工作,以备各方查验。
1.2 自动化监测地铁隧道结构变形监测可分为两部分:①测站点、基准点和监测点的布设; ②道床水平位移、垂直位移和隧道水平收敛自动化监测,自动检测系统组成如图 2所示。
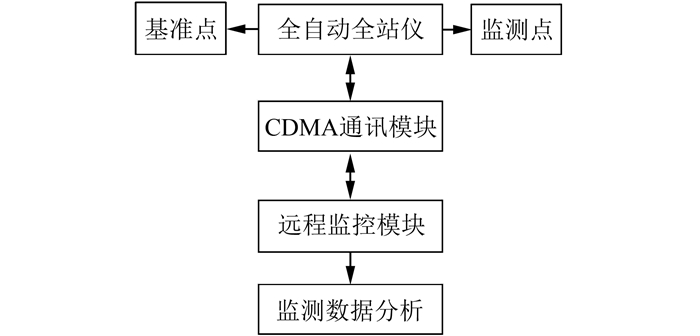 |
| 图 2 自动监测系统组成图 Fig.2 Composition of the Automated Monitoring System |
1) 自动监测系统的基本组成。自动监测系统由基准点、监测点、全自动全站仪、基站、通讯模块、监控模块、计算机、监测数据分析软件8部分组成。通讯方式采用CDMA(code division multiple access)技术,此技术可以实现无线通讯。
工作基站应设在隧道侧壁或不影响通车安全且有良好视野的位置,安装于基站的全自动全站仪与监测系统机房建立通讯联系,一般采用电信或移动的数据传输。由机房控制全站仪对基准点和监测点按一定的顺序进行逐点观测、记录、计算及自校,并将测量结果发送至机房存储,由机房计算机进行计算、整理、分析。具体监测流程如图 3所示。
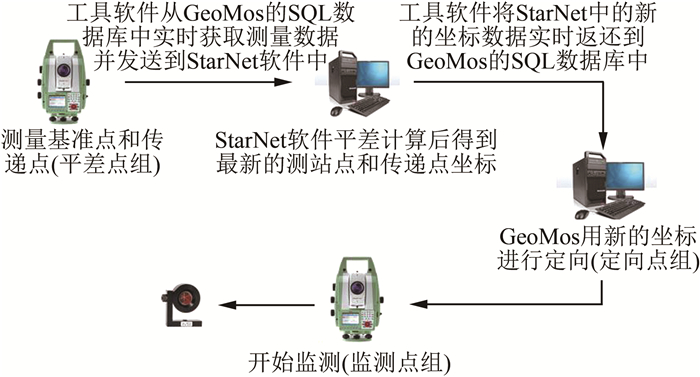 |
| 图 3 自动监测流程图 Fig.3 Flow Chart of Automatic Monitoring |
2) 工作基站及校核点设置。根据段隧道自动化监测技术要求,为使仪器能自动寻找目标,工作基点与变形监测点布设应满足最小仪器视场角要求,即要确保仪器视场角内只有1个监测点。全站仪正常视场角为1°33',对于100 m的距离视场直径为2.7 m。
工作基点的布设应满足保证仪器最小视场角,便于全站仪容易自动寻找目标。设置工作基点时,先安装仪器托架,然后再固定仪器。
3) 监测使用的平面、高程基准点。监测基准点根据实际情况选用,一般在远离施工影响外的10~15环距离的稳定位置布置4个以上稳固基准点(单侧2个以上基准点),自动化监测点布置如图 4所示。
 |
| 图 4 自动化监测点布置图 Fig.4 Automatic Monitoring Site Layout |
4) 监测点布设。在地铁隧道上行线及下行线区间中,基坑施工影响较大范围内(基坑围护结构边界与隧道管壁边界距离小于10 m)每5环布设一个监测断面; 位于施工影响相对较小范围内每10环布设一个监测断面。上、下行线隧道区间各形成监测断面60个。
基坑施工期间影响范围盾构区间,每5~10环设1个观测断面,可根据监测的具体情况适当加密,每个观测断面设4个监测点(道床上2个、侧壁2个),其中道床2个监测点可计算道床差异沉降、侧壁2个监测点可间接计算管径收敛。
基站的仪器托架以角钢预制,配强制对中基座,托架用膨胀螺丝锚固在观测墩或隧道壁上。
5) 盾构隧道结构水平位移和垂直位移自动化监测。根据地铁形变监测的要求和原则,拟采用特种工程测量仪器徕卡TM30系列全站仪进行监测[6]。
6) 计算原理与方法。在监测系统中,利用基准点坐标,采用多重实时差分技术求各变形点的坐标变化量。
2 精度分析 2.1 斜距的精度分析地铁隧道一般位于地下十几米乃至几十米,不受阳光照射,虽有通风井与外界通风,但仍保持相对稳定的温度和湿度。在地下空间监测中,气象改正应为一个极小值。为了实现变形监测的自动化,仪器架设的基准点和监测点应相对固定,宜布设基准网监测,根据基准网的测量信息,实时进行距离的大气折射率差分改正[9, 10]。
在自动极坐标差分测量系统中,监测站与基准点的仪器需固定在隧道侧壁上,保证它们之间的距离稳定不变。设基准站至某监测点的已知斜距为dJ0,在变形监测过程中,某一次实测的斜距为d'J,两者间的差值可以认为是因气象条件变化引起的,按式(2)可求出气象改正比例系数Δd为:
| $ \Delta d = \frac{{d_J^{'} - d_J^0}}{{d_J^{'}}} $ | (2) |
为了保证距离气象改正比例系数Δd的可靠性和准确性,在实际施测中,取多个在限差内的气象改正比例系数Δd的平均值用于距离测量的差分气象改正。
根据平均气象改正系数Δd,分别应用于监测站至每个基准点的距离,真实斜距dJ为:
| $ {d_J} = d_J^{'} - \Delta d \cdot d_J^{'} $ | (3) |
如果同一时刻测得某变形点的斜距为d'P,那么经气象差分改正后的真实斜距为:
| $ {d_P} = d_P^{'} - \Delta d \cdot d_P^{'} $ | (4) |
在地铁结构的变形监测中,所求的变形量均为相对初始值而言的,可以把基准点第一次观测的方位角H0Ji作为基准方位角,为保证基准方位角的准确性和稳定性,须多次观测,在限差范围内求其平均值。后续监测周期对基准点观测的方位角H'Ji与基准方位角相比,有一个“方位角差异”ΔHi:
| $ \Delta {H_i} = H_{{J_i}}^{'} - H_{{J_i}}^0 $ | (5) |
因地铁开动时会引起整个内部空间的振动,这一差异主要是因仪器不稳定引起水平观测零方向的变化。此差异对监测点的测量也有同等的影响。
对地铁结构进行变形监测时,所设立的基准点往往不止一个,一般要求影响区域的两端各两个基准点。由于测量存在偶然误差,且列车的通过会对仪器观测造成影响,故每个基准点的方位角变形差异ΔHi就有大有小,笼统地求平均值可能不能客观地表现这一差异。故提出了“基准角差分”。
假设设置的基准点有3个,分别为J1、J2、J3。3个基准点可以组成C32=3个基准角,可依据式(6)求出每个基准角在两期观测中的变化值:
| $ \Delta {H_{ij}} = \left( {H{{'}_{{J_i}}} - H{{'}_{{J_j}}}} \right) - \left( {H_{{J_i}}^0 - H_{{J_j}}^0} \right) $ | (6) |
在3个基准角的变化值ΔHij中,找出绝对值最小的一个角度,假设为ΔH13,用此角度两个基准点的“方位角差异”(即ΔH1、ΔH3)的平均值,作为仪器方位漂移的改正值[11]。
在监测点每周期的方位角测量值H'P中,同时加入由同周期基准点求得的“方位角差异”ΔH,可准确求得监测点的方位角HP:
| $ {H_P} = H{{'}_P} - \Delta H $ | (7) |
角度的测量误差还应考虑全站仪的系统误差,变形监测全站仪的测角误差一般要求为±0.5″。
2.3 计算公式综合以上各项差分改正,按极坐标计算公式可准确求的每周期各变形点的三维坐标:
| $ \left\{ \begin{array}{l} {X_P} = {d_P}\cdot{\rm{cos}}V\cdot{\rm{cos}}{H_P} + {X^0}\\ {Y_P} = {d_P}\cdot{\rm{cos}}V\cdot{\rm{sin}}{H_P} + {Y^0}\\ \;\;\;\;\;\;{Z_P} = {d_P}\cdot{\rm{sin}}V + {Z^0} \end{array} \right. $ | (8) |
式中,X0、Y0、Z0为监测站的坐标值; V为垂直角。
若以变形点第一周期的坐标值(XP1,YP1,ZP1)作为初始值,则各变形点相对于第一周期的变形量为:
| $ \left\{ \begin{array}{l} \Delta {X_P} = {X_P} - X_P^1\\ \Delta {Y_P} = {Y_P} - Y_P^1\\ \Delta {Z_P} = {Z_P} - Z_P^1 \end{array} \right. $ | (9) |
对式(9)两边微分并换成中误差形式,可导出以下极坐标差分三维坐标测量的精度估算公式:
| $ \left\{ \begin{array}{l} m_{{X_P}}^2 = {\rm{co}}{{\rm{s}}^2}H{z_P} \cdot m_{{d_P}}^2 + d_P^2\cdot{\rm{si}}{{\rm{n}}^2}H{z_P}\cdot{\left( {\frac{{{m_{H{z_P}}}}}{\rho }} \right)^2}\\ m_{{Y_P}}^2 = {\rm{si}}{{\rm{n}}^2}H{z_P} \cdot m_{{d_P}}^2 + d_P^2\cdot{\rm{co}}{{\rm{s}}^2}H{z_P}\cdot{\left( {\frac{{{m_{H{z_P}}}}}{\rho }} \right)^2}\\ m_{{Z_P}}^2 = m_{{h_P}}^2 \end{array} \right. $ | (10) |
式中,HzP、mdp、mhp分别为P点的角度改正、距离改正和高差改正数。
根据点位误差估计公式:
| $ {m_P} = \pm \sqrt {m_X^2 + m_Y^2 + m_Z^2} $ | (11) |
即可得到P点的点位中误差为:
| $ {m_P} = \pm \sqrt {m_{{d_P}}^2 + {{\left( {\frac{{{d_P}}}{\rho }} \right)}^2}m_{H{z_P}}^2 + m_{{h_P}}^2} $ | (12) |
以杭州市某地铁监测项目为例,项目基坑工程的最大设计开挖深度大于10 m,自身风险等级为二级,周边环境风险等级为二级,因此本工程监测等级可认为属于二级。若基坑施工期间出现严重的涌土涌砂、渗漏水乃至支护结构变形过大等异常情况时,则需将本工程等级提高至一级。
基坑距离地铁隧道27 m,影响线路总长167 m,在地铁隧道上行线及下行线区间中,在施工影响地铁隧道范围内每5环(6 m)布置一个监测断面,超过施工范围隧道外延40环按每10环(12 m)布置一个监测断面。监测结果如图 5所示。
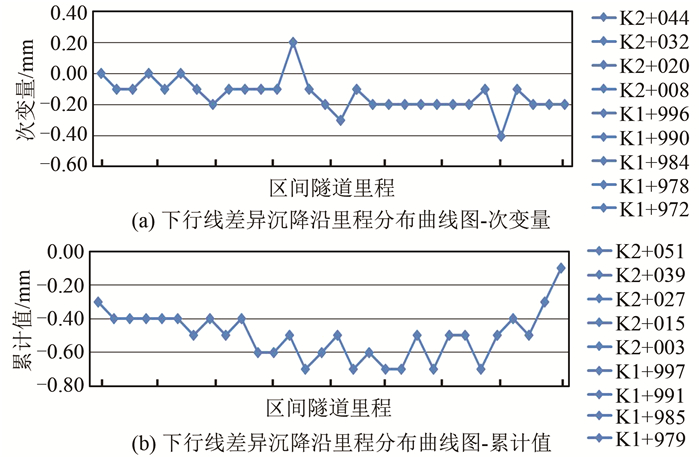 |
| 图 5 轨道水平差异分布图 Fig.5 Distribution of Orbital Settlement Differences |
从图 5中可以看出,水平位移呈平稳的波动状,极值都不大。在整个监测期间,车站主体向东位移,上下行相接的盾构区间除下行线大里程端的盾构隧道向西位移外,其余相接部分均向东位移。整个监测期间,主体基坑开挖后,上下行道床水平位移开始有所变动,至主体基坑回填后稳定,至今未达到报警值。依据监测结果显示,采用自动化监测,辅以人工测量的监测方法满足地铁隧道变形监测的要求。
| [1] |
张正禄, 孔宁, 沈飞飞, 等. 地铁变形监测方案设计与变形分析[J]. 测绘信息与工程, 2010, 35(6): 25-27. |
| [2] |
陈荣波. 城市地铁隧道断面检测系统研究与应用[J]. 测绘地理信息, 2017, 42(1): 115-118. |
| [3] |
徐秀川, 段双全, 宋超, 等. 影响地铁精密导线测距精度的因素及改正措施[J]. 测绘地理信息, 2015, 40(6): 35-37. |
| [4] |
邱冬炜, 梁青槐, 杨松林. 北京地铁隧道结构整体变形监测的研究[J]. 测绘科学, 2008, 33(S3): 16-17. |
| [5] |
赵宇, 谢谟文, 杜伟超. 城市轨道交通地面沉降雷达遥感监测分析[J]. 测绘地理信息, 2017, 42(5): 66-69. |
| [6] |
李豪, 邹进贵, 安祥生, 等. 徕卡MS50全站扫描仪在地铁隧道断面中的应用[J]. 测绘地理信息, 2018, 43(5): 68-71. |
| [7] |
钟金宁, 段伟, 田有良. 应用TM30进行地铁隧道变形自动监测的研究[J]. 测绘通报, 2011(7): 85. |
| [8] |
中国国家标准化管理委员会. 国家一、二等水准测量规范: GB/T 12897-2006[S]. 北京: 中国标准出版社, 2006
|
| [9] |
黄声享, 尹晖, 蒋征. 变形监测数据处理[M]. 武汉: 武汉大学出版社, 2010.
|
| [10] |
梅文胜, 陈雪丰, 周小波, 等. 盾构下穿既有隧道实时监测及其风险控制研究[J]. 武汉大学学报·信息科学版, 2011, 36(8): 923-927. |
| [11] |
陈龙飞, 金其坤. 工程测量[M]. 上海: 同济大学出版社, 1990.
|
 2021, Vol. 46
2021, Vol. 46

