| 小波与时间序列组合模型分析和预测建筑物沉降变形 |
2. 武汉大学灾害监测和防治研究中心, 湖北 武汉, 430079
2. Hazard Monitoring and Prevention Research Center, Wuhan University, Wuhan 430079, China
随着变形监测的快速应用与发展,学者们提出了各种不同的变形数据处理与预测模型,目前比较常用的模型有回归分析模型、灰色系统分析模型、时间序列分析模型、人工神经网络模型等[1]。变形监测中的变形数据都是各种变形因子组合作用的,不同的变形因子在不同的处理模型中所占的比重不同,导致不同的模型有不同的处理结果,难以反映实际的变形情况,用组合模型能够考虑到各种影响因子的组合作用,能更好地反映监测物的变形情况。时间序列分析模型是一种动态模型,对于各类变形监测数据有着很好的兼容性[2, 3],在处理非平稳的时间序列数据时,可用差分化剔除趋势项,但同时也导致因删除有效数据而造成预测精度降低[1]。小波分析模型中的小波变换能够有效地从时序数据中提取误差,基于此,本文结合各模型的优点,提出了利用小波分析和时间序列分析组合的方法来进行建筑物变形监测数据的分析与预报。
1 预测原理与方法步骤建立时间序列分析模型ARIMA(p, d, q)进行变形监测数据预测时,一般需要平稳的时间序列数据,但若观测的数据非平稳且包含有明显趋势时,就需要利用差分处理来去除时序数据的趋势项,留下随机项[3],但是变形监测的观测数据总存在误差,因此,它包含的趋势也会有误差,经差分处理去趋势后有可能造成有用资源的丢失,预测模型的预测精度也会降低。而小波分析在去除噪声方面非常有优势,可以利用小波分析去噪,减小观测数据的趋势误差,以此来提高预测精度[4-8]。
1) 对原始监测数据进行小波去噪。小波去噪的核心是对信号进行小波分解,然后对小波系数进行阈值化处理,由经过处理的小波系数重构原信号,得到真实信号的最优估值。
2) 对去噪后的数据进行时间序列的平稳性检测和平稳化处理。首先,做出去噪后的序列图,观察其平稳性(变形数据一般都呈现出一定的趋势,是非平稳数据,需对其平稳化);然后,对非平稳数据进行d阶差分,将其化为平稳序列。
3) 确定模型。做出平稳序列的自相关图,根据自相关图的截尾特性来确定自回归求和移动平均模型ARIMA(p, d, q)中的p、q值。
4) 对去噪后的数据建立ARIMA(p, d, q)模型。用相关软件进行建模,选出最优的模型,输出建模结果,并对其进行分析。
2 工程实例预测与效果分析长江紫都3期工程C片共有1#~10#建筑物、商业楼、小学建筑物及地下室等。为保证施工期间建筑物的安全性及质量的可控性,需对建筑物及地下设施进行沉降监测。沉降基准点建立在稳定可靠且距离长江紫都3期工程C片及地下室100 m以外的地方。沉降监测点的布设严格按照工程设计要求进行布设,观测严格按照相关标准规范进行。限于篇幅,这里只对长江紫都C块1#楼的监测数据进行分析。
2.1 沉降稳定性初步分析长江紫都C块1#楼各个监测点的沉降变形量如图 1所示,其中n1~n11为1#楼的11个监测点。监测时间从2014年3月1日到2016年1月15日,共686天, 总共监测了32期。
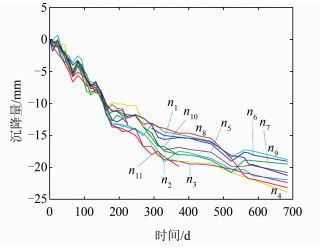 |
| 图 1 1#楼各个监测点的沉降变形图 Figure 1 Settlement and Deformation of the Individual Monitorin Stations of Building 1# |
由图 1可知,各点沉降趋势大致相同,最大沉降量为23.90 mm,最小沉降量为18.80 mm,沉降速度前期较快,后期逐渐变慢,平均沉降速度为0.031 mm/d,说明该建筑物已基本稳定,无异常情况。
2.2 沉降预测为了考察建筑物的沉降变形趋势,运用小波和时间序列组合模型进行分析预测[9]。限于篇幅,这里以n3沉降监测点为例进行分析。
1) 小波去噪。由于SymN系列小波在处理沉降数据上具有优越性,这里采用SymN系列进行去噪处理。经反复试验,对原始信号使用Sym4小波进行3层分解效果最好。分解后,采用Sym4小波基于Stein无偏似然估计SURE阈值的软阈值方法对变形监测数据进行去噪处理和残差分析。表 1列出了n3号点去噪前后的各期数据[10-12]。
| 表 1 去噪前后n3号点沉降数据 Table 1 Settlement Data of n3 Point Before and After Denoising |
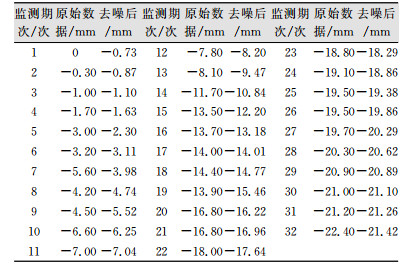 |
由表 1可以看出,去噪后的数据能较好地拟合原数据,可以平滑原数据中噪声引起的不平滑的部分,便于后续步骤的数据分析处理。
2) 序列平稳化及模型参数确定。去噪后的时间序列不是一个平稳的时间序列,它有明显的下降趋势,可对其进行差分处理,采用一阶差分和二阶差分使该序列平稳化。
二阶差分后的序列在零值附近上下波动,其图形比一阶差分后的序列更加平稳,因此,对二阶差分后的数据进行相关分析,得到自相关系数和偏自相关系数图,如图 2所示。由图 2可知,偏自相关系数在k=5后均落于置信区间内,可以取p=5或4,自相关系数在k=1处显著不为零,取q=1。
 |
| 图 2 自相关和偏自相关系数图 Figure 2 Graphs of Auto-Correlation Coefficient and Partial Auto-Correlation Coefficient |
3) 最优模型选择。运用spss软件对信号进行ARIMA(5, 2, 1)和ARIMA(4, 2, 1)建模。两次建模的统计量如表 2所示。
| 表 2 模型统计量 Table 2 Model Statistics |
 |
由表 2可知,在平稳R2的选择上,ARIMA(5, 2, 1)模型比ARIMA(4, 2, 1)略好,但在Ljung-Box统计中Sig.参数的比较方面,ARIMA(4, 2, 1)模型的Sig.值小于0.05,而ARIMA(5, 2, 1)模型的Sig.值远大于0.05,可见,ARIMA(4, 2, 1)模型的可信度更高,因此,选用ARIMA(4, 2, 1)模型进行建模。
4) 建模与预测。这里采用前30期数据进行建模分析,向后预测两期。图 3为对建模后的残差值进行相关性分析得到的自相关图。
 |
| 图 3 残差自相关和偏自相关图 Figure 3 Auto-Correlation and Partial Auto-Correlation of Residual Errors |
由图 3可知,经建模后的残差数据在零附近有很小的波动,可视为白噪声,说明该模型的信息提取比较充分,所建模型比较合适。建模后模型的拟合值与预测值均在限差范围之内,拟合效果较好,模型选择合适。
5) 结果分析。表 3列出了原始数据与建模后的拟合数据,同时也列出了预测的两期数据, 加粗的数据为预测值。
| 表 3 拟合值与原始值 Table 3 Fitting Values and the Initial Values |
 |
由表 3求得均方误差为0.69 mm。两期的预测值与实测值之间的误差分别为0.06 mm和0.05 mm,均在2倍中误差之内,预测精度较高,因此,该组合模型的分析和预测结果比较可信。
3 结束语本文采用小波分析与时间序列组合模型对长江紫都C块1#楼监测数据进行了处理分析和预测,结果表明,1#楼各点沉降趋势大致相同,该建筑物已基本稳定,无异常情况。以n3沉降监测点为例,先用小波分析去除粗差,然后采用ARIMA(4, 2, 1)模型对该建筑物的监测数据进行建模预测,效果较好。另外,用此方法对其他几栋楼的变形监测数据进行处理分析得知,其他各栋楼房的变形稳定,没有异常变形情况。
| [1] |
国计鑫. 小波分析与时间序列组合模型在变形监测分析预测中的应用研究[D]. 长安: 长安大学, 2014 |
| [2] | 黄声享, 尹晖, 蒋征. 变形监测数据处理[M]. 武汉: 武汉大学出版社, 2010 |
| [3] | JonathanD C, ChanK S. 时间序列分析及应用[M]. 北京: 机械工业出版社, 2010 |
| [4] | 李晓霞, 张建雄. 小波分析在变形监测数据处理中的应用[J]. 中州煤炭, 2015, (8): 105–108 |
| [5] | 倪华针, 洪飞. 基于时序分析的变形监测数据分析与预报[J]. 科技广场, 2014, (6): 6–9 |
| [6] | 何永红, 靳鹏伟, 文鸿雁. 基于不同预处理的多小波在变形监测数据处理中对比分析[J]. 工程勘察, 2013, (12): 61–65 DOI: 10.3969/j.issn.1000-1433.2013.12.014 |
| [7] |
朱云. 小波分析在建筑物动态监测数据处理和变形分析中的应用研究[D]. 河南: 河南理工大学, 2008 |
| [8] | 熊俊楠, 王泽根, 徐忠印, 等. 高层建筑物变形监测数据处理方法研究及工程应用[J]. 测绘科学, 2010, 35(S1): 69–71 |
| [9] | 丁宁, 孙英君, 崔健, 等. 高层建筑物变形监测数据处理与分析[J]. 测绘科学, 2011, 36(5): 93–94 |
| [11] | 刘闯, 花向红, 赵杰, 等. 基于小波去噪的高铁沉降预测模型研究[J]. 测绘地理信息, 2015, 40(1): 37–40 |
| [12] |
杜琨. 变形监测数据处理的方法研究[D]. 长沙: 中南大学, 2013 |
 2018, Vol. 43
2018, Vol. 43

