| 城市CORS网的基站稳定性分析研究 |
2. 自然资源部第一海洋研究所, 山东 青岛, 266033
2. The First Institute of Oceanography, MNR, Qingdao 266033, China
连续运行参考站系统(continuous operational reference system,CORS)系统是一种能够提供连续动态定位的空间参考框架和地球动力学参数等服务的信息系统[1],具有动态、实时、快速、高精度的特点[2]。CORS系统通常由用户管理中心、数据中心、参考站、通信系统、用户应用系统组成[3]。
目前,对于小范围内的CORS定位,观测1~2 h即可获得厘米级的定位结果,而对于大范围(数千米)、高精度(毫米或亚毫米级)的定位工作[4],需要长时间的静态观测。
本文结合中国香港的CORS系统,通过长时间静态GPS测量,得到连续测量的GPS数据,采用双差解算方法,分析该CORS网的静态解收敛性和基站坐标移动收敛性,进而对各基站的稳定性进行分析和比较。
1 城市CORS网的组成及分析城市CORS系统是在城市区域范围内,建立由若干个连续运行参考站、数据通信链路、数据中心和用户终端构成的局域网络,综合应用GNSS定位技术、计算机技术、数据通信和互联网(LAN/WAN)技术进行实时差分信息解算,实时地向不同类型、不同需要、不同层次的用户自动地提供经过检验的不同类型的GPS观测值(载波相位、伪距),各种改正数、状态信息,以及其他有关GPS服务项目的系统[5-7]。
香港的CORS系统是由18个CORS站组成,其中包括16个参考站和2个完整性监测站,对整个城市地区能够全覆盖,而本文选取其中的HKFN、HKKT、HKLT、HKSL、HKNP、HKMW、HKON、HKPC、HKSC、HKST、HKSS、HKWS共12个CORS站进行试验研究。
在城市CORS系统运行中,为获取高精度的GPS定位结果,通常要进行长时间的静态观测。通过长时间的连续跟踪观测,卫星的几何图形产生了较大的变化,从而使得卫星空间位置精度因子(position dilution of precision,PDOP)保持在较小的数值,也能够有效消弱随机误差的影响,从而提高观测的可靠性和精确性[8, 9]。
2 数学模型本文基于双差模式对香港CORS网的基站坐标进行解算。其双差模式的数学模型为:
| $ \varphi_r^s(t)=\frac{1}{\lambda} \rho_r^s(t)-N_r^s $ | (1) |
式中,φrs (t) 为t时刻的相位观测值;ρrs (t) 为t时刻的测站到卫星的几何距离;Nrs为t时刻相位的整周未知数。
在历元t时刻,在A、B、C 3个测站上同时对卫星s、k、m,进行观测,其中k为参考星,A为基准站,可得到双差观测方程为:
| $ \left\{\begin{array}{l} \varphi_{A B}^{k s}(t)=\frac{1}{\lambda} \rho_{A B}^{k s}(t)-N_{A B}^{k s} \\ \varphi_{A B}^{k m}(t)=\frac{1}{\lambda} \rho_{A B}^{k m}(t)-N_{A B}^{k m} \\ \varphi_{A C}^{k s}(t)=\frac{1}{\lambda} \rho_{A C}^{k s}(t)-N_{A C}^{k s} \\ \varphi_{A C}^{k m}(t)=\frac{1}{\lambda} \rho_{A C}^{k m}(t)-N_{A C}^{k m} \end{array}\right. $ | (2) |
其中,双差观测值可带入公式$\varphi_{A B}^{k s}(t)=\varphi_B^s(t)-\varphi_A^{\mathrm{s}}(t)+\varphi_B^k(t)-\varphi_A^k(t)$中,由双差观测值系数阵,可得出其相关性为:
| $ \mathit{\pmb{{\Sigma}}}_s=\sigma^2 C C^{\mathrm{T}}=\left[\begin{array}{cccc} 4 & 2 & 2 & 1 \\ 2 & 4 & 1 & 2 \\ 2 & 1 & 4 & 2 \\ 1 & 2 & 2 & 4 \end{array}\right] $ | (3) |
上述相关性矩阵为满秩矩阵,观测值之间的相关性较强,所以在基线网解算中必须要考虑观测值间的相关性[10]。
3 CORS网基站的稳定性分析本实验中,主要是从CORS网的静态解收敛性和基站坐标解算对CORS网基站稳定性进行分析。
3.1 静态解收效性分析在香港CORS系统中对静态解收敛性的分析,采用CORS站位为基准站,在2013年8月20日进行24 h的流动站测量,以流动站的解为真值,计算不同时间的不同方向上的基站分量的较差,得出其收敛度,结果如图 1所示。
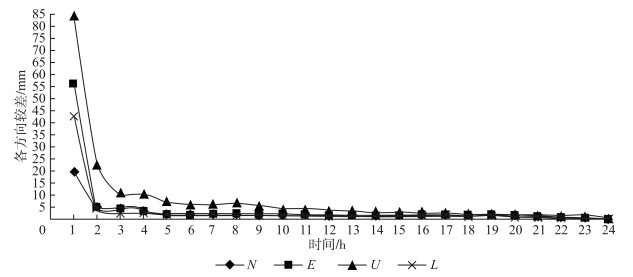 |
| 图 1 基站分量各方向收敛度 Fig.1 Degree of Convergence of Base Station Components in all Directions |
从图 1所示,连续观测3 h,平面N、E分量和基线长度L分量精度达到5 mm左右,而连续观测5 h时,精度即可达到3 mm内,继续观测对其精度影响不大;对高程U分量,需连续观测10 h后,收敛度才到5 mm,且延长观测时间,收敛度会有所提高。因而,在GPS精密测量时,需至少连续观测10 h,才能保证数据达到5 mm的精度。
3.2 CORS网基站坐标解算在对CORS网基站坐标解算,通过长时间观测,采用双差模式对CORS网的基站测量,解算得到其他各个基站的坐标,结合各个不同时间所得到的基站坐标,相互进行比较,从而对基站的稳定性做出分析,对分析后的结果进行统计,得出CORS网的各个基站的稳定性。
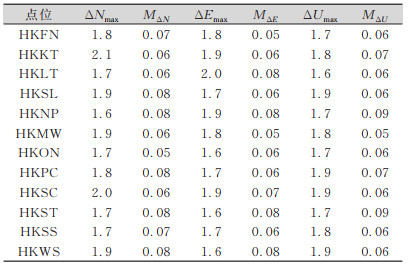
本实验对香港CORS站进行长时间静态测量,数据采集时间为2013-03-05—2013-08-31共180 d,并利用双差模型对观测得到的坐标值进行平差处理,得到CORS网中待测基站的点位算术平均值中误差及移动速度,结果如表 1、表 2所示。
| 表 1 待测基站点位较差统计表/mm Tab.1 Statistical Table of Point Position Difference of the Base Station to be Measured/mm |
 |
| 表 2 各基站的收敛速度/(10-6m·d-1) Tab.2 Convergence Speed of Each Base Station /(10-6 m·d-1) |
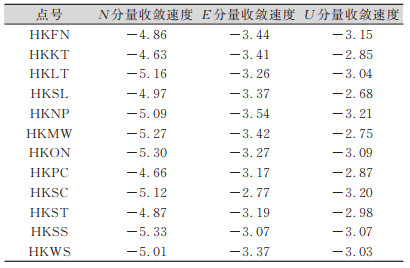 |
从表 1、表 2统计的数据可以看出,经过长时间的静态测量,CORS网基站的坐标值相对变化较小,待测基站各分量的较差小于或等于2.2 mm,算术平均值中误差小于或等于0.1 mm,各基站分量收敛速度小于-5.50×10-6 m·d-1,各个基站的坐标值变化很小,稳定性好,测量精度高。从上述算例结果表明,相比传统GPS精密定位,本文的算法在收敛时间和定位精度方面都有较大的改善,这也验证了该算法的正确性和可靠性。
4 结束语本文主要结合香港CORS网的建立和作用,在参考了许多国内外文献的基础上,处理了大量的数据,得到了一些结论:
1)对CORS系统的基站静态解收敛性分析,可以得到:连续观测4~5 h,平面N、E分量和基线长度L分量的精度可以到达3 mm;对高程U分量,需连续观测10 h,精度才能达到5 mm。所以在进行精密测量时,需连续测量10 h以上才能满足测量的需要。
2)对CORS系统的基站坐标稳定性进行分析,通过坐标解算可以得到基站的坐标值变化很小,稳定性好,测量精度高。CORS站点能够长时间、连续、稳定的高精度观测,并且可以有效提高整体解算精度,增加解算结果的可靠性。
现在,我国很多城市和地区都建立了CORS网,但由于各地经济发展极不平衡,同时各行业各部门对CORS网络的需求也很不相同(比如交通部门、地震部门、规划部门),导致我国CORS网络分布不均衡,这也需要国家对CORS网要统一规划,加强合作。
| [1] |
牟应录, 周星. 省域连续运行卫星定位综合服务系统建设[J]. 地理空间信息, 2015, 13(3): 34-35. |
| [2] |
李昌贵, 吕志平, 赵冬青, 等. CORS网络互联及虚拟CORS关键技术[J]. 测绘通报, 2008(1): 56-58. |
| [3] |
姚宜斌, 冯鑫滢, 彭文杰, 等. 基于CORS的区域大气增强产品对实时PPP的影响[J]. 武汉大学学报·信息科学版, 2019, 44(12): 1. |
| [4] |
高星伟. GPS/GLONASS网络RTK的算法研究与程序实现[D]武汉: 武汉大学, 2002
|
| [5] |
靳祥升, 高琼. 我国城市GPS综合服务系统建设进展[J]. 甘肃科技纵横, 2006(2): 29-30. |
| [6] |
戴连君, 过静珺, 谭志彬, 等. 北京市全球卫星定位综合应用服务系统[J]. 测绘通报, 2004(8): 38-41. |
| [7] |
李建, 吕志平, 乔书波. 连续运行参考站网的演化与发展趋势[J]. 测绘科学, 2008, 33(S3): 44-46. |
| [8] |
张西军, 唐卫明, 曾广鸿, 等. 广州市CORS系统实时动态定位精度测试[J]. 测绘信息与工程, 2008, 33(5): 6-8. |
| [9] |
过静珺, 王丽, 张鹏. 国内外连续运行基准站网新进展和应用展望[J]. 全球定位系统, 2008(1): 1-10. |
| [10] |
王霞迎. BDS/GPS基线解算算法研究[D]. 北京: 中国测绘科学研究院, 2014
|
 2022, Vol. 47
2022, Vol. 47


