| 基于实测数据的高填方工后预测模型研究 |
2. 陕西省特殊土工程性质与处理技术重点实验室,陕西 西安,710043
2. Shaanxi Key Laboratory of Engineering Behavior and Foundation Treatment for Special Soil, Xi'an 710043, China
随着经济的发展、科技的进步和产业结构的调整,中国进入了向现代城市型社会转变的历史时期,然而,中国西部的云贵高原、黄土高原等地区,受山地、黄土沟壑等特殊地形地貌的影响,城市发展受到很大的限制,特别是在耕地不能触碰的红线下,寻找可用于建设的土地,已经成为制约西部地区城市发展和城镇化建设的关键。实施平山造地工程,对未利用的荒山和沟谷通过工程或生物措施改造成为农用地或城市建设用地, 从而拓展城市发展空间,这种方法成为了西部地区城市发展的一种必然选择,但是,平山造地工程的沉降变形往往比较大,在填方体上进行工程建设最容易出现不均匀沉降造成的建筑开裂、管道断裂等工程问题。高填方工程沉降预测及控制是此类工程首要关注的重点。因此,根据施工过程中的监测数据对后续变形进行预测,从而为后续施工顺序安排和必要的安全防护措施准备提供一定的依据[1]。
目前,基于实测沉降时间数据的推算法,因其回避了理论计算的自身缺陷和计算参数值不准等因素,在各种工程中得到了广泛的应用[2],本文主要针对属于静态预测的对数曲线模型、指数曲线模型、双曲线模型以及抛物线模型,指出适于高填方沉降预测的方法[3-10]。
1 回归模型的基本原理 1.1 回归模型简介1) 对数曲线模型。其指数法方程为:
| $ {S_t}{\rm{ = }}a\ln \left( t \right) + b $ | (1) |
式中,t为时间;a、b分别为模型参数。
2) 指数曲线模型。其指数法方程为:
| $ {S_t}{\rm{ = }}\left( {1 - A{{\rm e}^{ - Bt}}} \right){S_m} $ | (2) |
式中,Sm为最终沉降量;t为时间;A、B为系数。
3) 双曲线模型。其指数法方程为:
| $ {S_t} = {S_0} + \frac{t}{{a + bt}} $ | (3) |
式中, t为从满载开始的时间,确定起点时间(t=0),可取填方施工结束日为t=0;S0为初始时t0时刻沉降量;a、b为双曲线的两个参数,将荷载不变后的实测数据经过回归求得的系数。
4) 抛物线模型。对于有些情况,沉降曲线在初期的沉降-时间对数坐标系中可由两部分组成,第一部分可由抛物线来拟合,第二部分即次固结部分可由直线拟合。两部分发生的量级和时间取决于土层固结后达到的孔隙比所对应的当量固结应力,只要运营期的有效应力小于预压期末的固结应力,次固结可以忽略不记。否则,就应该考虑次固结的影响。
实践证明,除有机质含量很高的土外,沉降量主要集中在第一部分,沉降曲线的一般表达式为:
| $ S = a{\left( {\lg t} \right)^2} + b\lg t + c $ | (4) |
式中, 参数a、b、c用最小二乘法确定。
1.2 回归模型预测效果判定为了判定各种回归模型的预测精度,通过3点进行评价:①回归离差平方和;②绝对误差P与止测日期误差P′;③长期沉降大小及规律。其中,绝对误差和止测日绝对误差为:
| $ \left\{ \begin{array}{l} P = \frac{{S - S'}}{S}\\ P' = \frac{{{S_{{\rm{止测日}}}} - {{S'}_{{\rm{止测日}}}}}}{{{S_{{\rm{止测日}}}}}} \end{array} \right. $ | (5) |
式中, S为现场实测沉降量; S′为相同时间的预测沉降量; S止测日为最后一次停止监测时沉降量; S′止测日为相应时间的预测沉降量。
2 实例分析本次选取某高填方工程工作区9个地表沉降监测点的连续监测数据作为拟合预测模型的依据,9个地表沉降监测点对应填土高度范围为22.6~104.4 m, 监测时长为530~955 d。有6个地表点分布于沟横截面填土厚度较大的沟中间位置,2个地表点位于沟横截面填土厚度较小的沟边侧位置且位于原地形斜坡上方,1个地表点位于主沟和支沟交叉位置的两沟横截面中间位置。最后时段沉降速率分布范围为0.01~0.208 mm/d。从填土厚度、位置特征等信息方面考虑,选取的地表点对全区地表点具有一定代表性。
本次试验选取地表点第1年(最接近365 d)工后沉降监测数据为回归依据,对不同的回归模型进行评价,以选取最优模型。如表 1和表 2所示。
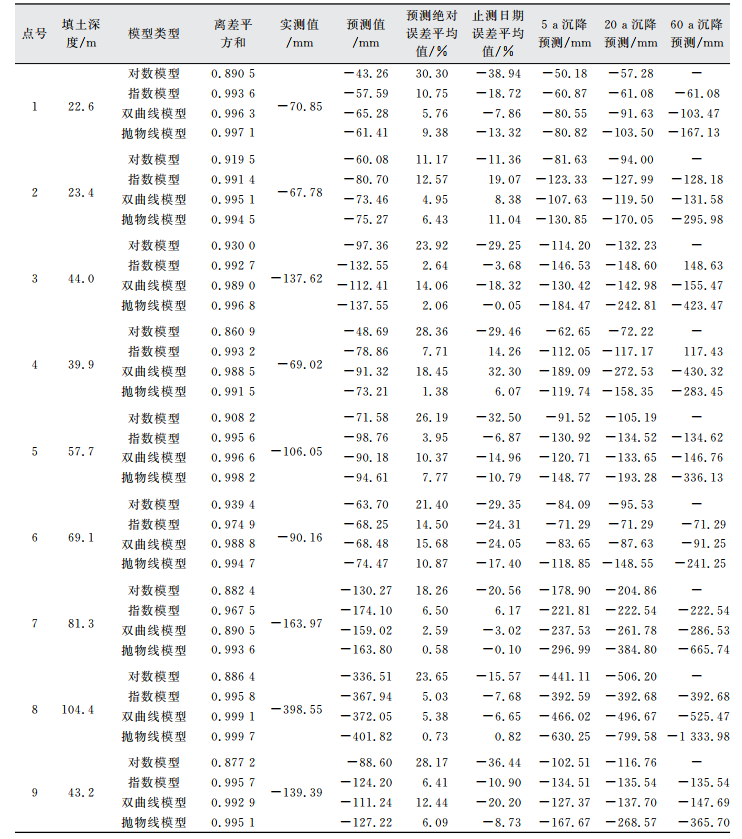
| 表 1 基于1 a监测沉降的回归模型预测结果汇总表 Tab.1 One Year Monitoring Subsidence Prediction Results Summary Based on Regression Model |
 |
| 表 2 基于1 a监测沉降的回归模型预测效果评价指标汇总表 Tab.2 One Year Monitoring Subsidence Prediction Effect Evaluation Summary Table Based on Regression Model |
 |
表 1中统计汇总的回归模型离差平方和、预测沉降量绝对误差平均值和止测期沉降量误差均能反映回归参数模型对于预测黄土高填方工后沉降的效果,离差平方和越大、两种误差越小,说明回归参数模型的预测结果越准确。表 2为每个测点基于1 a实测值回归的4种模型离差平方和、误差平均值、止测期沉降量误差的平均值以及置信水平95%条件下的置信区间。
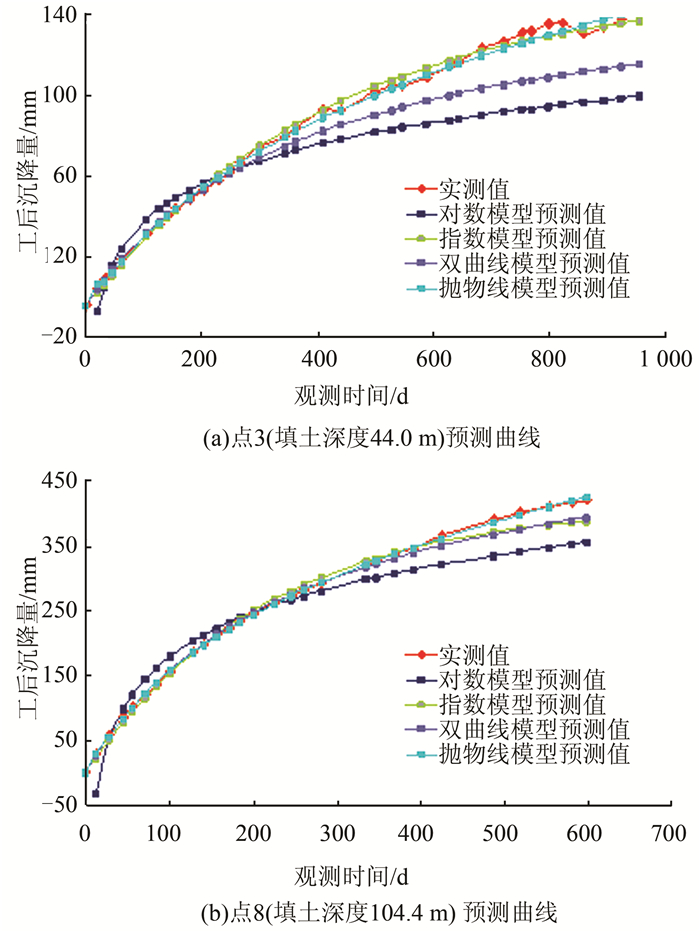 |
| 图 1 基于1 a监测沉降的回归模型沉降预测曲线 Fig.1 One Year Monitoring Settlement Settlement Prediction Curve Based on the Regression Model |
1) 指数模型、双曲线模型和抛物线模型的离差平方和平均值均大于0.98,依次为0.988 9、0.981 8和0.995 6,对数函数的离差平方和平均值仅为0.899 3。
2) 对比预测沉降量绝对误差平均值计算统计结果发现,所有抛物线模型预测沉降量绝对误差平均值最小,为5.03%;指数模型其次,绝对误差平均值为7.78%;双曲线模型绝对误差平均值为9.96%;对数模型绝对误差平均值最大为指数模型,达到23.49%,且有3个绝对误差平均值大于20%。
3) 对比止测期沉降量误差计算结果发现,抛物线模型预测的相对误差平均值最小为-3.61%;其次是指数模型的-3.63%;然后是双曲线模型的-6.04%;最差为对数模型的-27.05%。
3 结束语通过对不同监测时长的地表沉降进行4种曲线模型的回归分析,得到以下几点认识:
1) 在对数曲线模型、指数曲线模型、双曲线模型以及抛物线模型中,对数曲线模型回归预测效果最差,不适合用于黄土高填方工后沉降预测。
2) 指数曲线、双曲线以及抛物线回归预测效果较好,其中指数曲线和双曲线预测结果接近,预测误差基本在20%以内。虽然抛物线整体预测误差最小,基本在10%以内,但预测结果较前两种曲线大。
3) 随着回归分析的所用的监测数据时间越长,预测精度增大,预测效果越好。
| [1] |
王鹏, 孟灵飞, 李篷, 等. 回归分析在建筑物变形监测中的应用[J]. 测绘科学, 2013, 38(2): 187-188. DOI:10.3969/j.issn.1673-6338.2013.02.018 |
| [2] |
明祖涛, 游振兴, 张届, 等. 高速铁路桥隧沉降预测模型的研究[J]. 测绘通报, 2011(8): 17-19. |
| [3] |
黄声享, 尹晖, 蒋征. 变形监测数据处理[M]. 武汉: 武汉大学出版社, 2003.
|
| [4] |
潘林有, 谢新宇. 用曲线拟合的方法预测软土地基沉降[J]. 岩土力学, 2004, 25(7): 1053-1058. DOI:10.3969/j.issn.1000-7598.2004.07.010 |
| [5] |
杨涛, 戴济群, 李国维. 基于指数法的分级填筑路堤沉降预测方法研究[J]. 土木工程学报, 2005, 38(5): 92-95. DOI:10.3321/j.issn:1000-131X.2005.05.017 |
| [6] |
Bater D M, Watts D G.非线性回归分析及其应用[M].韦博成, 译.北京: 中国统计出版社, 1997
|
| [7] |
肖筱南, 欧阳克智. 新编概率论与数理统计[M]. 北京: 北京大学出版社, 2002.
|
| [8] |
王丽琴, 靳宝成, 杨有海. 黄土路堤工后沉降预测新模型与方法[J]. 岩石力学与工程学报, 2007, 26(11): 2370-2376. DOI:10.3321/j.issn:1000-6915.2007.11.026 |
| [9] |
王丽琴, 靳宝成, 杨有海, 等. 黄土路基工后沉降预测模型对比研究[J]. 铁道学报, 2008, 30(1): 43-47. DOI:10.3321/j.issn:1001-8360.2008.01.008 |
| [10] |
徐实. 湿陷性黄土地基铁路路基工后沉降规律研究[J]. 兰州交通大学学报, 2011, 30(4): 58-62. DOI:10.3969/j.issn.1001-4373.2011.04.013 |
 2018, Vol. 43
2018, Vol. 43

