| 非等间距改进灰色模型在基坑变形预测中的应用 |
城市地下工程变形对环境影响的监测及预报问题是关系到城市建设的一个重要课题。我国的预定目标和现在的发展现状预示将进入一个大规模开发地下空间资源的时代。在软土工程施工中,确保基坑,尤其是深基坑开挖的稳定性具有重要意义。
灰色理论自从创建以来,已经得到了广泛的应用,起初的灰色系统要求数据序列是等间距的[1]。但是在基坑工程中,监测的频率是不同的,而且存在数据的丢失,得到的监测序列往往是非等间距的。
国内很多学者对非等间距序列做出了大量研究[2-7],归纳起来大致分为两种:①基于赋权处理的模型;②基于等距处理的模型[3],这两种模型比较适合平稳的观测序列。如尹晖等将其应用到居民楼[3];梁永平等加入小波去噪将其应用到等间距序列的桥墩上[5];张冬菊等结合整体最小二乘将其应用到大坝变形中[7]。这些文献中的数据序列都比较平稳,数据波动小。
基坑工程监测点受基坑开挖的影响,往往会在短时间内产生较大的变形,现有的非等间距灰色模型在基坑应用中精度很低,无法处理突变数据的影响。本文在两种现有模型的基础上对时间做平滑,提出了基于改进赋权处理的动态灰色模型;对观测序列做平滑,提出了基于小波等距处理的动态灰色模型。然后在基坑的不同位置选取监测点进行模型检验,实验表明,这两种改进方法均有较好的适用性和精度。
1 改进模型 1.1 基于改进赋权处理的动态灰色模型设基坑某一监测点的观测序列为:
| $ {X^{\left( 0 \right)}} = \left\{ {{x^{\left( {\text{0}} \right)}}\left( {{t_1}} \right), {x^{\left( {\text{0}} \right)}}\left( {{t_2}} \right), \cdots , {x^{\left( {\text{0}} \right)}}\left( {{t_n}} \right)} \right\} $ |
式中,x(0)(ti)为ti时刻监测点的变形值,现有的赋权处理模型是以时间间隔为权,对原始序列做一次累加处理:
| ${x^{\left( {\text{1}} \right)}}\left( {{t_k}} \right) = \sum\limits_{i = 1}^k {{x^{\left( {\text{0}} \right)}}\left( {{t_i}} \right)} \Delta {t_i}, k = 1, 2, \cdots , n $ | (1) |
式中,
基坑监测点受施工的扰动比较大,在施工期间会受外力作用而在短时间内产生较大的变形,现有的模型并不能处理突变数据,所以需要模型重建。
单位时间内变形值可以表示为:
| $ {{v}_{i}}=\frac{\Delta {{x}^{\left( 0 \right)}}\left( {{t}_{i}} \right)}{\Delta {{t}_{i}}}, i=2, 3, \cdots , n $ | (2) |
式中,
| $ \left\{ \begin{align} &{\Delta {x^{\left( 0 \right)}}\left( {{t_i}} \right) = {x^{\left( 0 \right)}}\left( {{t_i}} \right) - {x^{\left( 0 \right)}}\left( {{t_{i - 1}}} \right)} \\ &{\Delta {t_i} = {t_i} - {t_{i - 1}}} \end{align} \right. $ |
令ρi=βvi, ρi为原始序列叠加的权,ρ1=1。β是为了保证原始序列最大时间间隔的一致:
| $ \beta = \frac{{{t_n} - {t_1}}}{{\sum\limits_{i = 2}^n {{v_i}} }} $ | (3) |
这样定权的优点是当变形速率大时(施工期间),累加序列适当放宽时间;当变形速率较小时(停工期间),累加序列适当压缩时间;当变形速率为负值时,累加序列变小,可以看做时间回退,以此来解决突变问题。
| $ {x^{\left( {\text{1}} \right)}}\left( {{t_k}} \right) = \sum\limits_{i = 1}^k {{x^{\left( {\text{0}} \right)}}\left( {{t_i}} \right)} {\rho _i}, k = 1, 2, \cdots , n $ | (4) |
得到序列:
| $ {X^{\left( {\text{1}} \right)}} = \left\{ {{x^{\left( {\text{1}} \right)}}\left( {{t_1}} \right), {x^{\left( {\text{1}} \right)}}\left( {{t_2}} \right), \cdots , {x^{\left( {\text{1}} \right)}}\left( {{t_n}} \right)} \right\} $ |
建立一阶微分方程:
| $ \frac{{d{x^{\left( 1 \right)}}}}{{dt}} + a{x^{\left( 1 \right)}} = u $ | (5) |
用最小二乘法可以估计参数
| $ \hat \varphi = {\left[{\hat a, \hat u} \right]^{\text{T}}} = {({\mathit{\boldsymbol{B}}^{\text{T}}}\mathit{\boldsymbol{B}})^{ - 1}}{\mathit{\boldsymbol{B}}^{\text{T}}}\mathit{\boldsymbol{Y}} $ | (6) |
式中,
| $ \mathit{\boldsymbol{Y}} = {\left[{{x^{\left( 0 \right)}}\left( {{t_2}} \right), {x^{\left( 0 \right)}}\left( {{t_3}} \right), \cdots , {x^{\left( 0 \right)}}\left( {{t_n}} \right)} \right]^{\text{T}}};\\ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \mathit{\boldsymbol{B}} = \\{\left[{\begin{array}{*{20}{c}} {-{z^{\left( 1 \right)}}\left( {{t_2}} \right)}&{-{z^{\left( 1 \right)}}\left( {{t_3}} \right)}&{\cdots }&{-{z^{\left( 1 \right)}}\left( {{t_n}} \right)} \\ 1&1&{\cdots }&1 \end{array}} \right]^{\text{T}}},\\ {z^{\left( 1 \right)}}\left( {{t_k}} \right) = \frac{1}{2}\left( {{x^{\left( 1 \right)}}\left( {{t_k}} \right) + {x^{\left( 1 \right)}}\left( {{t_{k - 1}}} \right)} \right)。$ |
将求取参数带入微分方程,可得离散解:
| $ {\hat x^{\left( 1 \right)}}\left( {{t_k}} \right) = \left[{{x^{\left( 1 \right)}}\left( {{t_1}} \right)-\frac{{\hat u}}{{\hat a}}} \right]{e^{ - \hat a\left( {{t_k} - {t_1}} \right)}} + \frac{{\hat u}}{{\hat a}} $ | (7) |
还原数据:
| $ {\hat x^{\left( {\text{0}} \right)}}\left( {{t_k}} \right) = \left( {{{\hat x}^{\left( {\text{1}} \right)}}\left( {{t_k}} \right)-{{\hat x}^{\left( {\text{1}} \right)}}\left( {{t_{k - 1}}} \right)} \right){\text{/}}{\rho _k} $ | (8) |
因为预测序列n+1…的ρk是未知的,需要做如下近似:
取j=1, 2…, m表示时序号,则有:
| $ {\hat x^{\left( 1 \right)}}\left( j \right) = \left[{{x^{\left( 1 \right)}}\left( {{t_1}} \right)-\frac{{\hat u}}{{\hat a}}} \right]{e^{ - \hat a\left( {j - 1}\right)}} + \frac{{\hat u}}{{\hat a}} $ | (9) |
还原数据:
| $ {\hat x^{\left( {\text{0}} \right)}}\left( j \right) = \left( {1 -{e^{\hat a}}} \right)\left[{{x^{\left( 1 \right)}}\left( {{t_1}} \right)-\frac{{\hat u}}{{\hat a}}} \right]{e^{ - \hat a\left( {j - 1}\right)}} $ | (10) |
t1对应时序1,若|ρn|比较小,表明变形已经趋向稳定,可以把tn后的每个时刻变形值通过上式拟合出来。
即:
| $\begin{matrix} {{\hat x^{\left( {\text{0}} \right)}}\left( {{t_k}} \right) = \left( {1 - {e^{\hat a}}} \right)\left[{{x^{\left( 1 \right)}}\left( {{t_1}} \right)-\frac{{\hat u}}{{\hat a}}} \right]{e^{ - \hat a\left( {{t_k} - {t_1} + 1} \right)}}} \\ {k = n + 1} \\ \end{matrix} $ | (11) |
若变形不稳定,比如基坑仍在开挖中,则此模型精度虽比现有模型的好,但也不佳,需要等开挖结束后做模型重建。
在预测下一个时刻tn+2的变形时,加入上一个时刻的变形预测值tn+1,去除老的信息t1时刻变形值,重建模型,以此类推,实现动态预测。
1.2 基于小波等距处理的动态灰色模型现有的基于等距处理的灰色模型建模思想是利用时间系数,把非等间距序列处理为等间距序列。处理过程如下:
1) 计算平均时间间隔。
| $\Delta {t_0} = \frac{{{t_n} - {t_1}}}{{n - 1}} $ | (12) |
2) 求每期观测时距与平均观测时距的单位时段系数。
| $ \varphi \left( {{t_k}} \right) = \frac{{{t_k} - {t_1} - \left( {k - 1} \right)\Delta {t_0}}}{{\Delta {t_0}}} $ | (13) |
3) 计算各期观测值差值。
| $ \Delta {x^{\left( 0 \right)}}\left( {{t_k}} \right) = \varphi \left( {{t_k}} \right){\left[{{x^{\left( 0 \right)}}\left( {{t_k}} \right)-{x^{\left( 0 \right)}}\left( {{t_{k-1}}} \right)} \right]} $ | (14) |
4) 重新构造等间距序列。
| ${y^{\left( 0 \right)}}\left( k \right) = {x^{\left( 0 \right)}}\left( {{t_k}} \right) - \Delta {x^{\left( 0 \right)}}\left( {{t_k}} \right) $ | (15) |
等间距序列为:
| $y_1^{\left( 0 \right)} = \left\{ {{y^{\left( {\text{0}} \right)}}\left( 1 \right), {y^{\left( {\text{0}} \right)}}\left( 2 \right), \cdots , {y^{\left( {\text{0}} \right)}}\left( n \right)} \right\} $ |
把非等间距序列通过上述变换处理为等间距序列后,现有的等距处理模型是对等间距序列建立微分方程进行求解。这样的做法与现有的赋权法一样,不能解决基坑工程中监测点中的受施工影响而产生的突变数据。
监测点受到基坑开挖的影响,产生了超出其正常变形值的突变值,我们可以把这部分突变当成噪声来处理。近年来,大量研究表面小波变换在消除噪声,数据平滑方面有比较好的应用,所以在建模过程中引入小波变换。
时间间隔不同产生的变形往往是不一样的,通常时间间隔越大,变形值越大。直接平滑非等间距观测序列没有考虑时间间隔的影响,存在把长时间内产生的较大变形值当作噪声消去的可能。预测结果精度低,适用性差。所以对等距处理后的等间距序列Y做小波去噪,然后再建立微分方程:
| $ {z^{\left( 0 \right)}}\left( k \right) = {y^{\left( 0 \right)}}\left( k \right) + n\left( k \right) $ | (16) |
式中,n(k)表示噪声,选择合适的小波基,分解层数,阈值来做小波去噪[8-10],得到新的等间距序列:
| $ z_1^{\left( 0 \right)} = \left\{ {{z^{\left( {\text{0}} \right)}}\left( 1 \right), {z^{\left( {\text{0}} \right)}}\left( 2 \right), \cdots , {z^{\left( {\text{0}} \right)}}\left( 3 \right)} \right\} $ |
利用z1(0)的一次累加数列z1(1)建立白微分方程:
| $ \frac{{{\text{d}}{z^{\left( 1 \right)}}}}{{{\text{d}}t}} + a{z^{\left( 1 \right)}} = u $ | (17) |
用最小二乘法可以估计参数
| $ \hat \varphi = {\left[{\hat a, \hat u} \right]^{\text{T}}} = {({\mathit{\boldsymbol{B}}^{\text{T}}}\mathit{\boldsymbol{B}})^{ - 1}}{\mathit{\boldsymbol{B}}^{\text{T}}}\mathit{\boldsymbol{Y}} $ | (18) |
式中,
| $ \mathit{\boldsymbol{B}} = {\left[{\begin{array}{*{20}{c}} {-{{\bar z}^{\left( 1 \right)}}\left( {\text{2}} \right)}&{-{{\bar z}^{\left( 1 \right)}}\left( {\text{3}} \right)}&{\cdots }&{-{{\bar z}^{\left( 1 \right)}}\left( n \right)}\\ 1&1&{\cdots }&1 \end{array}} \right]^{\text{T}}},\\ {\bar z^{\left( 1 \right)}}\left( k \right) = \frac{1}{2}\left( {{{\bar z}^{\left( 1 \right)}}\left( k \right) + {{\bar z}^{\left( 1 \right)}}\left( {k - 1} \right)} \right)。$ |
将求取参数带入微分方程,可得离散解:
| $ {\hat z^{\left( 1 \right)}}\left( k \right) = \left[{{z^{\left( 0 \right)}}\left( 1 \right)-\frac{{\hat u}}{{\hat a}}} \right]{e^{ - \hat a\left( {{\text{k - 1}}} \right)}} + \frac{{\hat u}}{{\hat a}} $ | (19) |
| $ {\hat z^{\left( 0 \right)}}\left( k \right) = \left( {1 - {e^{\hat a}}} \right)\left[{{z^{\left( 0 \right)}}\left( 1 \right)-\frac{{\hat u}}{{\hat a}}} \right]{e^{ - \hat a\left( {{\text{k - 1}}} \right)}} $ | (20) |
还原为非等间距序列
| $\begin{matrix} {{{\hat{x}}}^{\left( 0 \right)}}\left( k \right)= \\ {\left( {1 - {e^{\hat a}}} \right)\left[{{x^{\left( 0 \right)}}\left( {{t_1}} \right)-\frac{{\hat u}}{{\hat a}}} \right]{e^{ - \hat a\left( {{t_k} - {t_1}} \right)/\Delta {t_0}}}, k > 1} \\ \end{matrix}\ $ | (21) |
在预测下一个时刻tn+2的变形时,加入上一个时刻的变形预测值tn+1,去除老旧的信息t1时刻变形值重建模型,以此类推,实现动态预测。
2 实例与分析为了说明本文基于改进赋权处理的动态灰色模型和基于小波等距处理的动态灰色模型的适用性和经典,本文采用两个实例进行计算分析比较。并设模型1表示现有的基于赋权处理的灰色模型;模型2表示现有的基于等距处理的灰色模型;模型3表示基于改进赋权处理的动态灰色模型;模型4表示基于小波等距处理的动态灰色模型。文中各模型1、模型2、模型3、模型4中数值表示预测值。
模型精度通过后验差比值C和小误差概率P来检验, 检验标准见表 1。
| 表 1 灰色模型精度等级[5] Tab.1 1 The Precision Grade of Gray Model |
 |
模型精度等级=max{C所在等级,P所在等级}。
2.1 基坑工程开挖道路沉降点预测选用上海市浦东新区的某一基坑工程中的基坑与道路共同沟中的某一监测点GN68。监测数据见表 2所示。受基坑开挖施工的影响,该点随着时间的变化变形并不平稳,含有较多的突变数据,本实例旨在验证本文所述的两种改进模型在这种情况下比现有模型更有优越性。
| 表 2 GN68号点监测数据 Tab.2 GN68Point Monitoring Data |
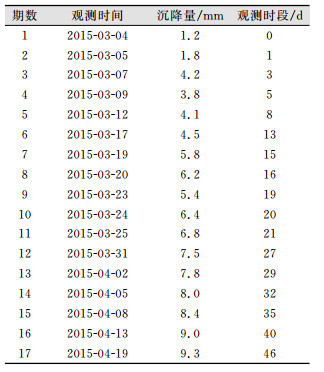 |
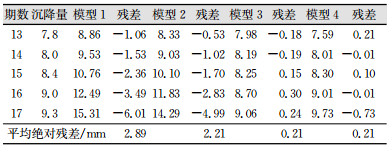
以前12期数据建立模型,后5期数据做预测。不同模型的预测结果见表 3所示。模型精度评价见表 4所示。
| 表 3 GN68号点不同预测模型结果比较/mm Tab.3 Comparison of the Results of Different Prediction Models of GN68 Point/mm |
 |
| 表 4 GN68号点模型精度评价 Tab.4 The Precision Evaluation of GN68 Point Model |
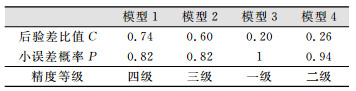 |
从表 3 GN68号点的预测结果可以看出,现有的等距处理模型和现有的赋权处理模型随着期数的增加残差急剧增加,现有的赋权处理模型精度等级四级,现有的等距处理模型精度等级三级,不适合基坑工程监测点的预测预报。而本文所提出的两种模型,基于改进赋权处理的动态灰色模型和基于小波等距处理的动态灰色模型的结果精度很高,基于改进赋权处理的动态灰色模型的最大残差仅有0.3 mm,精度等级一级,基于小波等距处理的动态灰色模型精度相对较低,最大残差达到0.73 mm,精度等级二级。
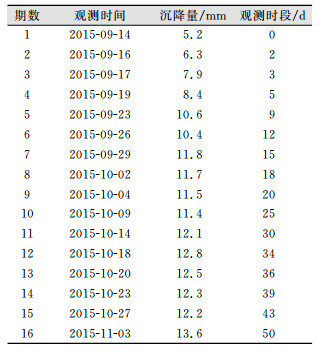
2.2 基坑不同位置沉降点预测为了考察本文所述模型在基坑不同位置的适用性,从基坑其他位置选取两个监测点:坑外地表沉降监测点DB12和地下管线位移监测点M16,具体监测数据见表 5、表 6。
| 表 5 DB12号点监测数据 Tab.5 DB12 Point Monitoring Data |
 |
| 表 6 M16号点监测数据 Tab.6 M16 Point Monitoring Data |
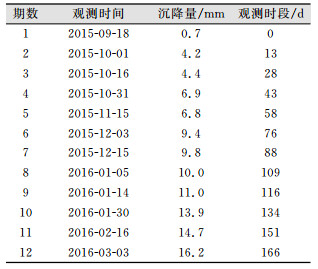 |
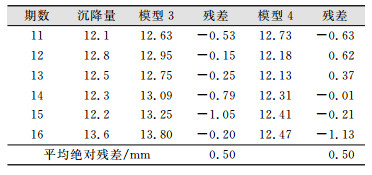
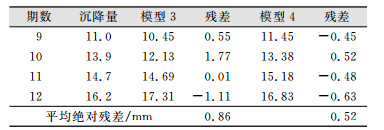
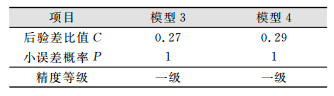
DB12号点选取前10期数据建立模型,后6期数据做预测;M16号点选取前8期数据建立模型,后4期数据做预测。预测结果见表 7、表 8。模型精度评价见表 9、表 10。
| 表 7 DB12号点预测结果/mm Tab.7 DB12 Point Prediction Results/mm |
 |
| 表 8 M16号点预测结果/mm Tab.8 M16 Point Prediction Results/mm |
 |
| 表 9 DB12号点模型精度评价 Tab.9 The Precision Evaluation of DB12 Point Model |
 |
| 表 10 M16号点模型精度评价 Tab.10 The Precision Evaluation of M16 Point Model |
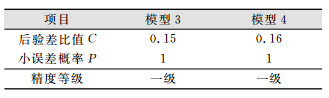 |
从预测结果和模型精度可以看出本文所述两种模型在基坑不同位置的适用性,精度都很好。其中,基于改进赋权处理的动态灰色模型更适用于时间跨度短,数据序列经突变后逐渐平稳的时间序列,基于小波等距处理的动态灰色模型更适合时间跨度较长的时间序列,能够进行一定的突变预测。这两种模型在基坑变形预测上有不错的优势,适合基坑工程监测点的预测预报。
3 结束语本文针对现有的非等间距模型的缺陷,建立了适合基坑工程监测点的非等间距模型,结果表明,本文所述模型精度更高,适合于基坑工程中不同位置的监测点。改进的赋权处理动态灰色模型更适合于时间跨度短,突变后逐渐平稳的监测点,时间跨度变长后精度变低,而基于小波等距的动态灰色模型在时间跨度比较长的序列中也有比较好的应用。在基坑施工中,把两个模型相结合来进行预测,能够保证基坑工程的安全性。综上所述,本文所述模型在基坑的变形处理中值得推广,有很大的实用价值。
| [1] |
邓聚龙. 灰理论基础[M]. 武汉: 华中科技大学出版社, 2002.
|
| [2] |
王穗辉. 误差理论与测量平差[M]. 上海: 同济大学出版社, 2010.
|
| [3] |
尹晖, 周晓庆, 张晓鸣. 非等间距GM(1, 1)建模方法对比分析及应用[J]. 测绘工程, 2017, 26(2): 1-4. |
| [4] |
梁永平, 严丽萍. 基于小波消噪的动态灰色桥墩沉降预测模型[J]. 测绘地理信息, 2017, 42(6): 65-68. |
| [5] |
朱军桃, 李亚威, 等. 建筑物沉降监测中的改进灰色模型[J]. 测绘科学, 2017, 42(11): 85-91. |
| [6] |
陈鹏宇. 非等距GM(1, 1)模型在沉降预测中的应用探讨[J]. 大地测量与地球动力学, 2017, 37(7): 709-714. |
| [7] |
张冬菊, 黄声享. 基于整体最小二乘的灰色模型在大坝变形分析中的应用[J]. 工程勘察, 2017(12): 55-59. |
| [8] |
康超, 黄声享, 李洋洋. 小波去噪和新陈代谢GM(1, 1)相结合应用于变形预报[J]. 测绘地理信息, 2015, 40(6): 46-48. |
| [9] |
魏玉明, 党星海, 杨鹏源, 等. 加权GM(1, 1)模型在变形监测中的应用研究[J]. 工程勘察, 2012, 40(4): 82-84. |
| [10] |
彭振斌, 张闯, 彭文祥, 等. GM(1, 1)模型背景值构造的不同方法与应用[J]. 东北大学学报(自然科学版), 2017, 38(6): 869-873. |
 2019, Vol. 44
2019, Vol. 44

