| 一种多波束声呐数据的可视化截取方法 |
2. 国家测绘地理信息局第七地形测量队, 海南 海口, 570203;
3. 海岛(礁)测绘技术国家测绘地理信息局重点实验室, 山东 青岛, 266590
2. The 7th Institute of Topographic Surveying, National Administration of Surveying, Mapping and Geoinformation, Haikou 570203, China;
3. Key Laboratory of Surveying and Mapping Technologyon Island and Reef, National Administration of Surveying, Mapping and Geoinformation, Qingdao 266590, China
随着计算机技术、高精度定位技术等相关高新技术的迅速发展, 多波束声呐测量系统获得了极大的发展, 在水深测量中已成为主要的测量方式[1]。多波束声呐测量系统能够在与航迹垂直的平面内一次给出成百上千个测量点, 是一种全覆盖式的测量[2], 因此导致数据量急增, 呈现出海量数据特性。针对此问题, 需要从海量的多波束声呐数据中截取特定区域的数据。
多波束声呐数据类型包括水深、反向散射强度和水柱影像数据, 精密水深数据能够获取目标的三维形状, 反向散射强度成像能够反演目标属性, 兼有二维声图像和三维目标探测的功能, 能够直观反映出海底的实际情况[3]。CARIS HIPS&SIPS是应用最为广泛的多波束数据后处理软件之一, 尤以海量多波束测量数据处理见长, 但是该软件并没有特定区域数据的截取功能。Fledermaus软件、Hypack软件同样没有特定区域数据的截取功能。但Surfer软件可以利用“白化”(blank)功能截取特定区域的地形数据[4], 该软件是一个功能齐全的三维可视化和表面建模软件, 被广泛用于地形数据格网化以及三维可视化等方面[5], 但是在数据处理时, 使用“白化”功能需要边界数据文件(.bln), 即边界点的具体坐标, 缺点是操作复杂, 且只能针对格网化后的数据(.grd)进行处理, 并不能获得特定区域的原始多波束声呐数据; ArcGIS软件中的ArcToolbox, 利用提取分析功能中的按掩膜提取, 可以实现区域数据的截取, 但是同样只能截取格网化后的多波束数据, 并不能截取原始的多波束数据。
可视化截取是保证多波束声呐数据高效处理的重要环节, 针对这一关键问题, 本文提出了一种多波束声呐特定区域数据的可视化截取算法。以多波束水深数据为研究对象(其他数据的处理方法类似), 在构建格网DEM(digital elevation model)模型的前提下, 完成多波束声呐数据的可视化; 结合数据分块算法与动态调度, 以及多边形截取模型, 实现特定区域数据的快速截取。
1 多波束声呐数据的可视化截取方法多波束声呐数据的可视化截取的关键技术是数据可视化与准确、快速地截取, 本文分别通过绘制格网DEM的阴影地貌图、分块建模来实现。可视化截取的主要实现步骤如下:①首先将多波束数据通过反距离加权插值方法进行格网化, 获得标准格网文件[6]; ②绘制格网DEM的阴影地貌图, 实现数据的可视化; ③对数据进行数据分块处理以及动态调度, 提高数据截取的速度; ④通过在地貌图上选取闭合多边形区域构建多边形截取模型, 实现多波束声呐特定区域数据的快速截取。
1.1 海底地形可视化 1.1.1 阴影法可视化技术阴影法是根据假定光源对地面照射所产生的明暗程度, 用浓淡不一的墨色或彩色沿斜坡绘制其阴影, 得到随光照近似连续变化的色调, 造成明暗对比, 使地貌的分布、起伏和形态特征具有一定的立体感, 直观的表达地面起伏变化, 在二维平面上显示出三维地貌[7], 便于观测者手工准确地选择截取区域。
基于规则格网DEM, 计算每个格网点的相对辐射值, 进而转换成光照强度, 最后绘制出阴影地貌图[8]。其相对辐射值的计算公式为:
| $ {I_R} = {G_{{\rm{max}}}} \times ({\rm{cos}}\left( {A-\alpha } \right){\rm{sin}}S{\rm{cos}}\beta + {\rm{cos}}S{\rm{sin}}\beta ) $ | (1) |
式中, IR为格网点灰度值; Gmax为最大灰度值, 一般取255;A为格网点的坡向, 范围是0~360°; S为格网点的坡度[9], 范围是0~90°; α为太阳方位角, 即光源的方向, 范围是0~360°; β为太阳高度角, 即太阳光与地面的夹角, 范围是0~90°。其中, 太阳方位角与太阳高度角人为确定, 可见, 得到光照强度的关键点是求取格网点的坡度与坡向。
坡度S和坡向A的计算公式分别为:
| $ S = {\rm{arctan}}\sqrt {f_x^2 + f_y^2} \times 180/\pi $ | (2) |
| $ A = 180^\circ-{\rm{arctan}}\frac{{{f_y}}}{{{f_x}}} + 90^\circ \frac{{{f_x}}}{{\left| {{f_x}} \right|}} $ | (3) |
式中, fx是东西方向的水深变化率; fy是南北方向的水深变化率。本文采用三阶反距离平方权差分法计算fx和fy。根据3×3的局部窗口进行计算, 图 1为差分DEM计算图(其中(a, b, …, i)为各格网点的水深值)。
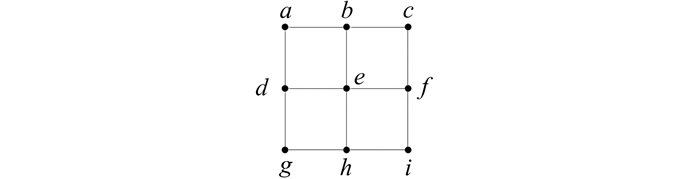 |
| 图 1 差分DEM计算示意图 Fig.1 Schematic Diagram of Differential DEM |
判断出需要参与计算的网格点, 最终计算出中心格网点的fx和fy:
| $ {f_x} = \frac{{c-a + 2\left( {f-d} \right) + i-g}}{{8d}} $ | (4) |
| $ {f_y} = \frac{{a-g + 2\left( {b-h} \right) + c-i}}{{8d}} $ | (5) |
由于多波束声呐数据量大, 在图形绘制过程中容易出现画面停顿及显示延迟现象[10]。为了解决上述问题, 提高绘制与刷新的速度, 本文采取了双缓存绘图算法。
双缓存实现的具体方法如下:1)首先定义一个显示设备对象; 2)定义一个位图对象; 3)建立与屏幕显示兼容的内存显示设备; 4)创建兼容位图; 5)将位图选择贮存; 6)先用背景色将位图清除干净; 7)绘制地形图; 8)将内存中的位图拷贝到屏幕上进行显示; 9)释放资源。
1.2 数据截取方法 1.2.1 数据分块与动态调度策略由于多波束声呐数据量巨大, 海量的数据规模会超出计算机内存的存储极限, 因此, 在截取数据之前, 必须对数据进行分块, 划分成若干规模较小的地形子块, 根据需要将数据动态地调入, 从而提高数据截取的速度。
数据分块是指将同一层面上的数据分割成大小合适的地形数据子块[11], 然后将所需要的地形子块加入内存进行处理。本文采取的地形数据划分方法是均匀分块, 即把整个地形平均划分成M×N个子块, 每一个地形子块的大小均相同。
数据动态调度是指依据需求高效准确地加载需要的地形数据块、释放不需要的数据块, 主要通过预加载和多线程加速实现。
预加载就是定义一个稍大的区域, 除了从外存中读取所需范围内的数据块, 再预先读取周边的一些地形子块到内存缓存中, 从而在数据更新时不需要直接从外存读取更新的地形子块, 直接从内存中读取, 从而加快数据处理效率。本文采用九宫格缓冲区预处理方法, 就是确定多边形截取区域的顶点之后, 在内存中加载该地形子块以及该子块对应的8个相邻地形子块。
多线程加速是指在一个进程中同时运行两个线程:主线程负责地形绘制, 子线程负责数据调度。多线程加速流程图如图 2所示。
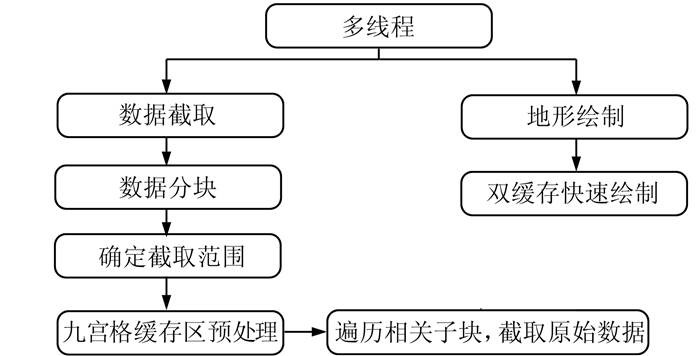 |
| 图 2 多线程流程图 Fig.2 Flow Chart of Multithread |
确定多边形截取区域的顶点之后, 采取九宫格缓冲区预处理方法, 从内存中加载各个顶点所在地形子块以及该子块对应的8个相邻地形子块; 然后, 依次判断各个地形子块的4个顶点的坐标是否属于截取范围, 若其中至少一个顶点坐标属于截取范围, 则遍历该子块的原始多波束声呐数据, 进而获取该子块在截取范围内的所有数据; 若4个顶点的坐标均不属于截取范围, 则该子块的所有数据不再进行遍历。
数据分块算法与动态调度策略不必加载和遍历所有的原始多波束声呐数据, 在一定程度上提高了数据截取的速度。
1.2.2 数据截取根据在阴影地貌图上所选取的闭合多边形区域, 构建多边形截取模型; 分别获取各个边界点的屏幕坐标, 进而转换成实际坐标, 确定截取范围; 再依据数据分块算法以及数据动态调度, 判断多波束声呐原始数据的各离散点是否属于截取范围; 最终输出该截取范围内的所有多波束原始数据。
坐标转换过程中, 须根据格网DEM绘制的阴影地貌图进行屏幕坐标计算, 完成实际坐标转换。由于DEM是标准的格网数据, 因此可以根据格网点所在的行数和列数进行绘制。即首先确定第一行第一列的格网点在屏幕中的坐标, 再依据图幅范围和横纵方向的格网点数依次确定每个格网点的屏幕坐标。以VC6.0开发平台为例, 阴影地貌图在VC6.0客户区的位置及格网点坐标计算如图 3所示。
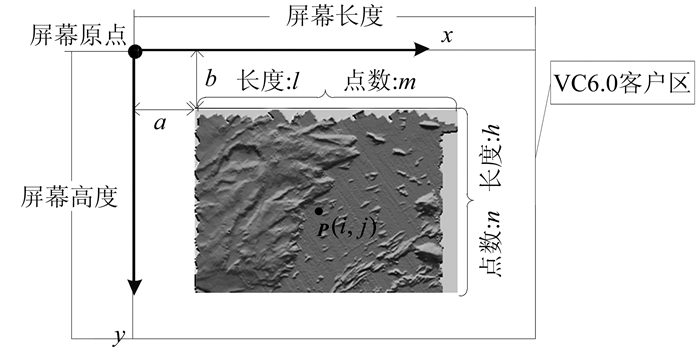 |
| 图 3 坐标计算示意图 Fig.3 Schematic Diagram of Coordinate Calculation |
由图 3可知, x坐标值的变化量Δx与y坐标值的变化量Δy为:
| $ \left\{ \begin{array}{l} \Delta x = {x_{{\rm{max}}}}-{x_{{\rm{min}}}}\\ \Delta y = {y_{{\rm{max}}}}-{y_{{\rm{min}}}} \end{array} \right. $ | (6) |
x轴方向相邻两格网点间的x坐标差值xp与y轴方向相邻两格网点间的y坐标差值yp分别为:
| $ \left\{ \begin{array}{l} {x_p} = \Delta x/m\\ {y_p} = \Delta y/n \end{array} \right. $ | (7) |
单位长度的x坐标差值xl与y坐标差值yl分别为:
| $ \left\{ \begin{array}{l} {x_l} = \Delta x/l\\ {y_l} = \Delta y/h \end{array} \right. $ | (8) |
假设已知第一行第一列格网点的实际坐标为(xmin, ymin), 则可知第i行第j列格网点P的实际x坐标与y坐标分别为:
| $ \left\{ \begin{array}{l} {x_{i, j}} = {x_{{\rm{min}}}} + j \times {x_p}/{x_l} = {x_{{\rm{min}}}} + j \times \\ (\Delta x/m)/(\Delta x/l) = {x_{{\rm{min}}}} + j \times l/m\\ {y_{i, j}} = {y_{{\rm{min}}}} + i \times {y_p}/{y_l} = {y_{{\rm{min}}}} + i \times \\ (\Delta y/n)/(\Delta y/h) = {y_{{\rm{min}}}} + i \times h/n \end{array} \right. $ | (9) |
由若干个类似P点的格网点构成闭合的多边形区域即可构建多边形截取模型。根据上述算法, 完成坐标转换, 得到多边形顶点实际坐标, 进而确定截取数据的范围。
2 实验与分析为了验证本文算法的有效性, 对实测多波束数据进行了可视化截取。研究数据为南海某海域多波束测深数据, 平面覆盖范围约390 km×280 km, 水深范围约为320 ~7 200 m。采用Seabeam 2100系统采集, 其测量范围为50~11 000 m, 包括12 kHz和36 kHz两个工作频率。在Surfer软件中同样设置太阳方位角为315°和太阳高度角为45°, 显示该格网DEM, 如图 4所示。
 |
| 图 4 Surfer软件显示的地形图 Fig.4 Topographic Map Displayed by Surfer Tool |
2.1 地形可视化结果分析
通过反距离加权插值算法格网化得到规则格网DEM, 设置太阳方位角为315°, 太阳高度角为45°, 基于VC6.0绘制阴影地貌图, 以实现数据的可视化, 显示效果如图 5所示。
 |
| 图 5 海底阴影地貌图 Fig.5 Seafloor Shadow Geomorphological Map |
比较图 4和图 5可知, 采用相同的数据源、太阳方位角和太阳高度角, 本文提出的可视化算法与Surfer软件功能类似, 能够正确地显示出海底地形的整体起伏变化; 并且由于采取了双缓冲绘图, 使得地形图的绘制与显示速度与Surfer软件没有明显差别; 但本文算法在地形起伏较大区域表达的精细程度不如Surfer软件, 并没有遗漏重要的特征物。
2.2 多边形区域数据截取结果分析本文采用的标准格网文件维数为1 500×1 100, 共165万个水深格网点, 对应的原始数据有8 000万水深散点。在绘制的阴影地貌图上选取了4个边界点, 组成了闭合多边形截取区域, 如图 6所示。
 |
| 图 6 截取区域 Fig.6 Area of Extracted Data |
通过上述计算方法, 程序自动获取4个边界点的屏幕坐标, 进而转换成实际坐标, 最终得到选取的闭合区域内的多波束原始数据。
为判断提取的原始数据是否正确, 将此数据进行格网化, 得到相应的格网DEM, 并且绘制该格网DEM的阴影地貌图, 如图 7所示。
 |
| 图 7 截取后的多波束数据阴影地貌图 Fig.7 Shadow Geomorphological Map of Extracted Data |
由图 6和图 7可知, 所提取的原始多波束数据的范围, 与选取的多边形区域范围一致。采用本文的可视化截取算法能够实现多波束声呐特定区域数据的多边形快速截取, 便于高效分析海底特定目标物以及恢复数据编辑过程中误删的特征物。
3 结束语针对多波束内业处理中, 高效分析海底目标地物以及恢复误删的特征物的需求, 本文对多波束声呐数据的可视化截取问题进行了研究。在构建格网DEM模型的基础上, 实现数据的可视化; 根据数据分块算法构建多边形截取模型, 实现多波束声呐特定区域数据的可视化快速截取。
根据实测数据分析表明, 该方法具有较好的直观性。其中的数据可视化功能便于在地貌图上准确选取所需区域; 截取效率和精度高, 能够从测区的海量数据中快速而准确地截取特定区域多波束声呐的原始数据。
| [1] |
阳凡林, 李家彪, 吴自银, 等. 浅水多波束勘测数据精细处理方法[J]. 测绘学报, 2008, 37(4): 444-457. |
| [2] |
赵建虎. 现代海洋测绘[M]. 武汉: 武汉大学出版社, 2012.
|
| [3] |
Djikpesse H, Sobreira J F F, Hill A, et al. Recent advances and trends in subsea technologies and Seafloor properties characterization[J]. The Leading Edge, 2013, 32(10): 1 214-1 220. DOI:10.1190/tle32101214.1 |
| [4] |
吴卫国. Surfer:网格化与白化处理在数据扩边中的应用—以1:5万水系沉积物测量成图为例[J]. 物探与化探, 2015, 39(3): 602-605. DOI:10.11720/wtyht.2015.3.28 |
| [5] |
孟静娟, 赵俐红, 阳凡林, 等. SUFER在海底地形表达中的应用[J]. 科技创新与应用, 2014(23): 294. |
| [6] |
张锦明, 郭丽萍, 张小丹. 反距离加权插值算法中插值参数对DEM插值误差的影响[J]. 测绘科学技术学报, 2012, 29(1): 51-56. |
| [7] |
赵玮丹, 江文萍, 李鸣. 数字地貌晕渲的信息量度研究[J]. 测绘地理信息, 2016, 41(3): 64-66. |
| [8] |
陈艳丽, 李少梅. 基于坡度坡向的地貌晕渲实现研究[J]. 测绘科学, 2008, 33(S3): 181-182. |
| [9] |
陈楠, 王钦敏, 汤国安, 等. 6种坡度提取算法的应用范围分析—以在黄土丘陵沟壑区的研究为例[J]. 测绘信息与工程, 2006, 31(4): 20-22. |
| [10] |
冯志红, 赵拥军, 李光茂. 消息调度模型下一种改进的双缓存地图漫游算法[J]. 测绘科学, 2013, 38(4): 86-90. |
| [11] |
赵庆. 大规模地形数据调度与绘制技术研究与实现[D]. 成都: 电子科技大学, 2011
|
 2018, Vol. 43
2018, Vol. 43


