| GNSS多系统伪距差分定位算法及结果分析 | [PDF全文] |
2. 羲和时空(武汉)网络科技有限公司,湖北 武汉,430079
2. Xihe Space Time (Wuhan) Network Technology Co., Ltd., Wuhan 430079, China
伪距差分定位是差分GNSS定位技术的一种,相较于载波差分定位,伪距差分无需解算周跳和模糊度,定位时间短,效率高[1];相较于伪距单点定位,伪距差分通过改正数消除了空间相关误差,从而克服了电离层和对流层模型改正时,由于模型不准确而导致的改正误差,拥有更高的定位精度。通常,在距基准站20 km以内,伪距差分的定位精度可以达到亚m级[2]。
随着中国BDS导航系统和欧盟Galileo导航系统的建设,多系统组合导航定位已成为发展趋势之一[3]。多系统组合导航定位提供了更多的可用卫星,改善了卫星的空间几何结构,从而提高了卫星导航系统的可用性、可靠性和精确性。
多系统伪距差分定位具有伪距差分定位时间短、精度较高的优点,也具备了多系统组合的更多可用卫星和良好卫星空间结构的优点,具有很高的应用价值。近年来国内外有许多学者对多系统伪距差分进行了研究。文献[4]通过内插模型,将多个基准站的改正数归算到某一虚拟参考站上,再播发给用户,完成GPS/BDS伪距差分;文献[5]利用卡尔曼滤波替代普通伪距差分定位中的最小二乘,进行动态的GPS/BDS伪距差分;文献[6, 7]分别研究了GPS/GLONASS双系统单基准站和GPS/GLONASS双系统多基准站伪距差分定位。文献[8]研究了GPS/BDS/GLONASS 3系统基于多基准站的伪距差分,其处理方法与文献[4]类似,通过将同一网格内的参考站改正数归算到网格中心点后,再播发给用户。文献[3]首次研究了系统间偏差(inter-system bias, ISB)在GPS/BDS/GLONASS/Galileo伪距差分中的应用,在初始若干个历元将各系统间的ISB当做待估参数并进行初始化后,便可将待估参数减为3个坐标参数和1个钟差参数,其结果表明,在可见卫星数少(小于8)且对接收机各系统间ISB特性充分了解时,加入ISB较传统的伪距差分水平方向可提高60%,高程方向可提高50%。
在上述研究中,对多系统伪距差分的研究基本围绕着双系统和3系统进行,未考虑到Galileo系统。文献[3]研究考虑加入ISB在4系统伪距差分中的提高效果,由于ISB不仅和卫星系统有关,也和接收机型号有关,故而该方法不具有普适性。在Galileo提供初始服务后,可接收到的Galileo卫星越来越多,这使GPS/BDS/GLONASS/Galileo 4系统组合定位可行。因此,本文采用了一组CORS(continuous operation reference station system)站4系统静态数据和1组车载4系统动态数据,采用单基准站伪距差分的方法,对4系统伪距差分定位的精度进行了分析和评定,并与GPS单系统、GPS/BDS双系统和GPS/BDS/GLONASS 3系统伪距差分的定位结果进行了对比。此外,为了进一步提高伪距差分的定位精度,本文在伪距差分前用Hatch滤波对伪距观测值进行了平滑处理。
1 伪距差分定位模型GPS/BDS/GLONASS/Galileo伪距差分定位系统,其空间部分由GPS卫星、BDS卫星、GLONASS卫星和Galileo卫星组成,地面部分是由基准站B和流动站M组成。在研究多系统时必须考虑ISB,系统间偏差包含了系统时间偏差和系统间信号的接收机硬件延迟[9]。由于系统间偏差的存在,4系统伪距差分定位需要为每个系统设置一个钟差参数,因而对4系统伪距差分,需要设置3个坐标参数和4个接收机钟差参数共7个待估参数[10]。
基准站B对卫星j的伪距观测方程为:
| $ \left\{ \begin{array}{l} {P^j}_B = {\rho ^j}_B + c({\rm{d}}{t^s}_B - {\rm{d}}{t^j}_s) + {I^j}_B + {T^j}_B + {\varepsilon ^j}_B\\ {\rho _B} = {\rm{ }}\sqrt {{\rm{(}}{X_B} - {X_j}){^2} + {\rm{ (}}{Y_B} - {Y_j}){^2} + {\rm{ (}}{Z_B} - {Z_j}{)^2}} \end{array} \right. $ | (1) |
式中,PBj为基准站B至卫星j的伪距观测值;ρBj为基准站B至卫星j的几何距离;dtBs、dtsj分别为接收机钟差和卫星j钟差,其中,s代表卫星导航系统,其取值为G、C、R和E,分别代表GPS、BDS、GLONASS和Galileo;IBj、TBj分别为基准站B的电离层误差和对流层误差;εBj为伪距观测噪声及其他非模型化误差;(XB, YB, ZB)为基准站已知坐标;(Xj, Yj, Zj)为根据卫星j发射信号时刻的卫星位置。
由式(1)可以得到基准站B对卫星j的伪距改正数为:
| $ \Delta {\rho ^j}_B = {P^j}_B - {\rho ^j}_B = c({\rm{d}}{t^s}_B - {\rm{d}}{t^j}_s) + {I^j}_B + {T^j}_B + {\varepsilon ^j}_B $ | (2) |
流动站M对卫星j的伪距观测方程为:
| $ {P^j}_M = {\rho ^j}_M + c({\rm{d}}{t^s}_M - {\rm{d}}{t^j}_s) + {I^j}_M + {T^j}_M + {\varepsilon ^j}_M $ | (3) |
式中,PMj为流动站M至卫星j的伪距观测值;ρMj为流动站M至卫星j的几何距离;dtMs、dtst分别为接收机钟差和卫星j钟差; IMj、TMj分别为流动站M的电离层误差和对流层误差;εMj为伪距观测噪声及其他非模型化误差。
在一定的空间范围内,基准站与流动站的大气误差(电离层、对流层延迟)具有空间相关性,此时可近似认为基准站与流动站的对流层延迟和电离层延迟相等,即IBj≈IMj,TBj≈TMj,因此,流动站M对卫星j的观测方程加上改正数后为:
| $ \left\{ \begin{array}{l} {P^j}_M - \Delta {\rho ^j}_B = {\rho ^j}_M + c({\rm{d}}{t^s}_M - {\rm{d}}{t^s}_B) + {\varepsilon ^j}_M\\ {\rho ^j}_M = {\rm{ }}\sqrt {{\rm{(}}{X^0}_M - {X_j}){^2} + {\rm{ (}}{Y^0}_M - {Y_j}{)^2} + {\rm{ (}}{Z^0}_M - {Z_j}{)^2}} \end{array} \right. $ | (4) |
式中,(XM0, YM0, ZM0)为流动站M的近似坐标。
令tMB, s=dtMs-dtBs,即在估计时,将流动站M的接收机钟差和基准站B的接收机钟差之差作为一个参数进行估计,其中,s代表卫星导航系统。
将tMB, g(流动站M与基准站B接收机GPS钟差之差)、tMB, c(流动站M与基准站B接收机BDS钟差之差)、tMB, r(流动站M与基准站B接收机GLONASS钟差之差)、tMB, e(流动站M与基准站B接收机Galileo钟差之差)和流动站坐标XM, YM, ZM设为7个未知参数,利用改正后的伪距观测值构建观测方程。(XM0, YM0, ZM0)为流动站M的初始坐标,对应的改正项为δx, δy, δz,通过泰勒级数展开对伪距观测方程进行线性化[8],线性化后的误差方程可表示为:
| $ \mathit{\pmb{V}} =\mathit{\pmb{A}}\delta \mathit{\pmb{X}} - \mathit{\pmb{LP}} $ | (5) |
式中,P为GPS/BDS/GLONASS/Galileo系统在融合系统中的权比分配矩阵。通常多系统组合的定权方差有基于高度角的先验定权方法和验后方差估计定权法。本文同一系统内观测值根据卫星高度角定权,系统间权比分配根据各系统的广播星历和各系统的伪码速率,文献[11, 12]给定了固定的权比,系统间权比为GPS:BDS:GLONASS:Galileo=5:3:2:5。
当共视卫星多于7颗时,流动站M通过最小二乘法进行解算为:
| $ \delta \mathit{\pmb{X}} = {\rm{ (}}\mathit{\pmb{A}}{^{\rm{T}}}\mathit{\pmb{PA}}{{\rm{)}}^{-1}}\mathit{\pmb{A}}{^{\rm{T}}}\mathit{\pmb{PL}} $ | (6) |
式(6)通过迭代计算,当满足给定的收敛阈值时结束循环,进而求出δX中改正项δx, δy, δz,即可按照[XM YM ZM]-1=[X0+δx Y0+δy Z0+δz]-1求出流动站M的三维坐标(XM YM ZM)。
2 实验验证与结果分析基于上述的模型和方法,笔者编制了GNSS多系统伪距差分定位的基准站差分改正数生成程序模块和流动站差分定位程序模块,以便对上述的伪距差分定位方法及定位效果进行测试验证。
在基准站差分改正数生成模块和流动站差分定位模块,程序会进行周跳探测与相位平滑伪距处理[13]。基准站差分改正数生成程序部分,对伪距观测值进行平滑后,通过已知的基准站坐标和平滑后的伪距观测值,计算出差分改正数并传递给流动站差分定位模块;在流动站差分定位模块进行伪距平滑并且接收到差分改正数后,程序根据接收到的改正数对相应的伪距观测值进行改正,再利用改正后的伪距观测值进行单点定位,求出流动站的坐标。
2.1 静态实验实验静态数据选用的是香港昂坪(HKNP)和香港坪洲(HKPC)的CORS站的观测数据。实验数据时段为2017年6月5日0点到12点(UTC)共12 h,采样率1 s,基线长约为15.4 km,截止高度角设为10°。本次实验选取HKNP作为基准站,HKPC作为流动站,数据解算时采用单频,GPS、BDS、GLONASS、Galileo的频点选择分别是L1、B1、L1、E1。
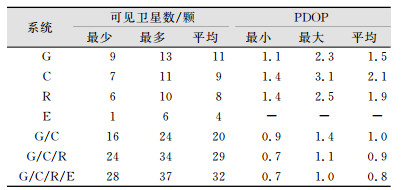
表 1给出了各系统的平均可见卫星数和卫星在空间分布的平均几何强度因子(position dilution of precision, PDOP)值。表 1中的G、C、R、E分别代表GPS、BDS、GLONASS和Galileo。图 1是观测时段内各系统可见卫星数目和对应的PDOP以及GPS/BDS/GLONASS/Galileo 4系统组合的可见卫星数目和PDOP值。从表 1和图 1可以看出,在观测时段内,每增加一个卫星系统,平均可增加4~11颗卫星,4系统的组合卫星数始终多于28颗,可见卫星数目有大幅度提高,卫星数的增加改善了空间的星座结构,其PDOP值不超过1.0,可保证良好的定位精度。由于Galileo卫星数目较少,无法进行单系统定位,所以PDOP值中没有Galileo系统的PDOP统计。
| 表 1 各系统可见卫星数目及PDOP Tab.1 Number of Available Satellites and PDOP for Different System |
 |
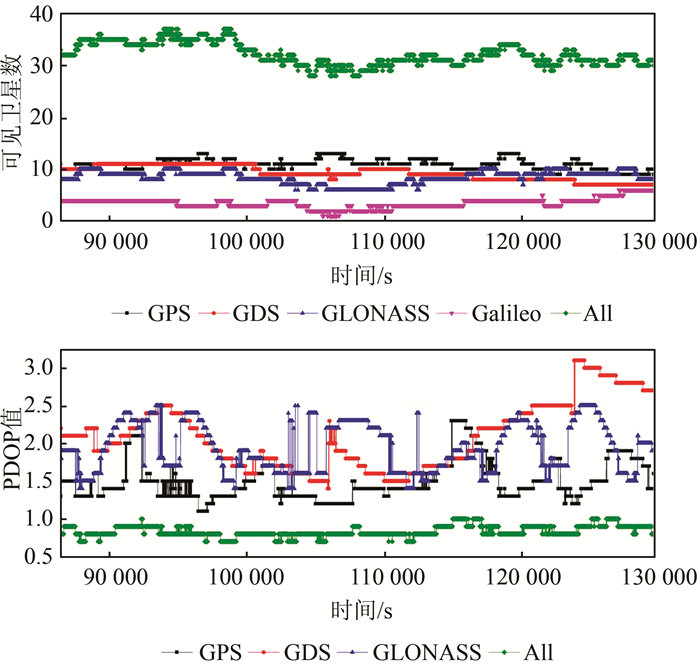 |
| 图 1 各系统可见卫星数目及PDOP Fig.1 Number of Available Satellites and PDOP for Different System |
为了分析GPS/BDS/GLONASS/Galileo 4系统伪距差分定位性能,分别以GPS单系统、GPS/BDS双系统、GPS/BDS/GLONASS 3系统以及GPS/BDS/GLONASS/Galileo 4系统共4种方案进行伪距差分定位解算,并将GPS/BDS/GLONASS/Galileo 4系统的定位结果与HKPC站已知精确坐标求差,将所得各分量偏差转化到站心坐标系(E,N,U)下,偏差时间序列如图 2所示。
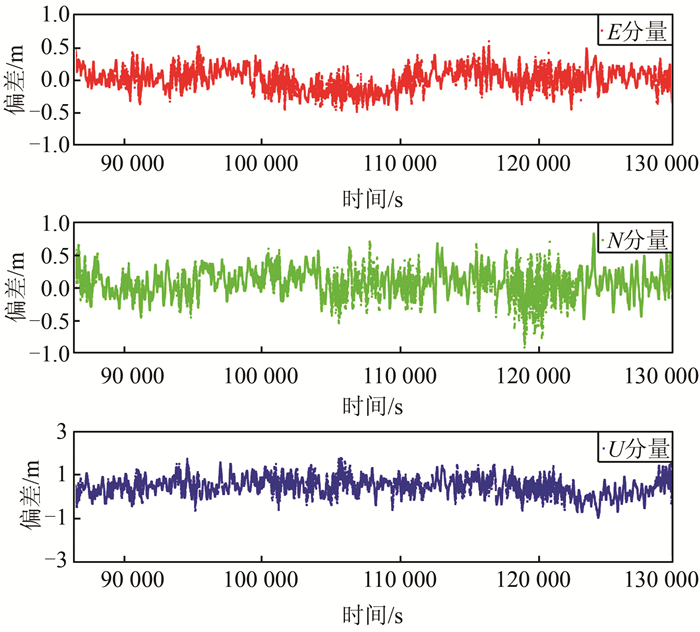 |
| 图 2 静态4系统E、N和U方向偏差时间序列图 Fig.2 Bias Time Series of E, N and U for Four Systems of Static Mode |
为进一步分析,表 2中统计了各解算模式偏差的RMS值以及相对于GPS单系统解算模式的改进率。
| 表 2 静态4种解算方案RMS Tab.2 RMS of Four Solutions of Static Mode |
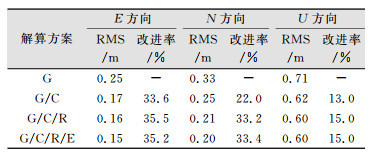 |
由表 2可以看出,GPS/BDS/GLONASS/Galileo 4系统伪距差分在E、N、U各分量较GPS单系统分别提高了35.2%、33.4%、15.0%,提高效果显著。GPS/BDS/GLONASS/Galileo 4系统伪距差分相较于GPS/BDS/GLONASS 3系统伪距差分的改进率并没有较为明显的提高,这是因为现阶段可接收到的Galileo卫星数目较少,增加的冗余观测值不多,但可以看到,在N方向,GPS/BDS/GLONASS/Galileo 4系统的RMS较GPS/BDS/GLONASS 3系统伪距差分的RMS有一定的提高。
2.2 动态实验动态数据采集于2016年10月27日,采集地点为武汉梁子湖大道。基准站架设在梁子湖大道路旁,选用Trimble NetR9接收机,天线型号为Trimble Zephyr Geodetic,采样率为1 s,截止高度角为10°。流动站数据采集来自车载数据,将天线安装在车顶支架上,天线型号与基准站天线型号一致,为Trimble Zephyr Geodetic天线,接收机为NovAtel 638,截止高度角10°,采样率1 s。为获取动态数据,安装了天线的车在梁子湖大道来回折返。实验数据时段为3:00:00~4:59:59(UTC),共2 h公共时段。数据解算时采用单频,GPS、BDS、GLONASS、Galileo的频点选择分别是L1、B1、L1、E1。
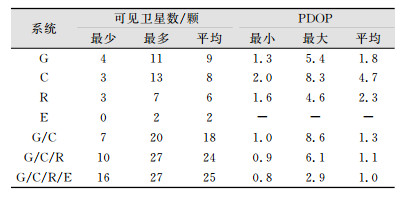
表 3给出了各系统的平均可见卫星数和平均PDOP值。图 3为公共时段内各系统的可见卫星数目及PDOP值。从表 3和图 3可以看出,4系统的可见卫星数目至少有16颗,足够进行伪距差分定位,且其PDOP均值为1,通常在PDOP小于2.5 h即可保证良好的定位精度,可见4系统的可用性较单系统有很大的提高。
| 表 3 各系统可见卫星数目及PDOP Tab.3 Number of Available Satellites and PDOP for Different System |
 |
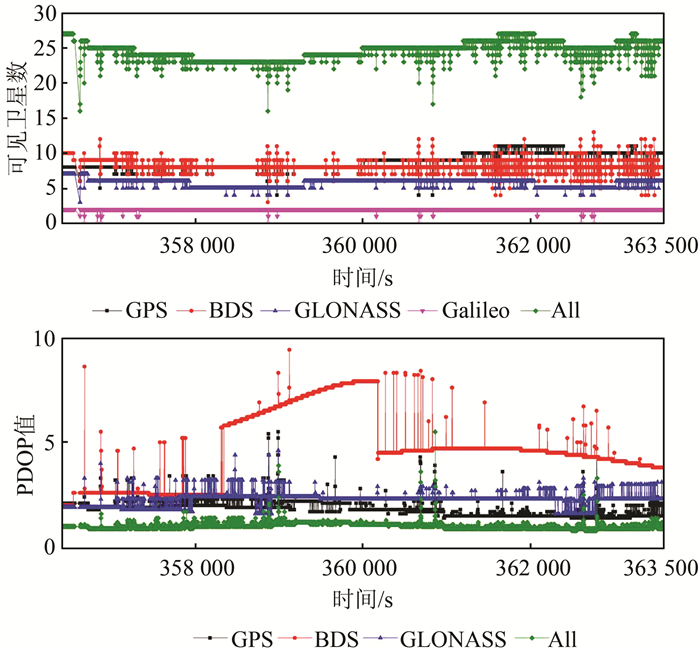 |
| 图 3 各系统可见卫星数目及PDOP Fig.3 Number of Available Satellites and PDOP for Different System |
图 4为观测时段内基准站与流动站之间距离变化图。通过图 4可以看出,搭载天线和接收机的车在不断折返跑,从斜率可看出汽车的移动速度较为均匀。
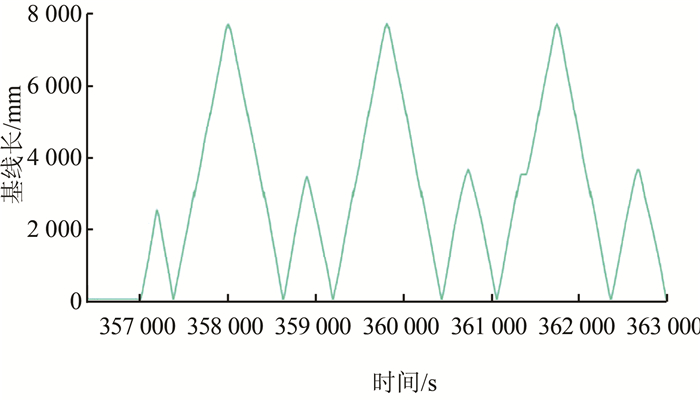 |
| 图 4 基线长度时间序列图 Fig.4 Baseline Length Time Series |
为了研究GPS/BDS/GLONASS/Galileo 4系统的定位精度,用NovAtel公司研发的GrafNav GNSS数据处理软件,采用实时动态测量(real-time kinematic, RTK)模式进行求解。目前RTK短基线(< 20 km)的精度可以达到cm级,其精度远高于伪距差分,因此,用RTK的结果当作真值参考值,进行后续的评定和分析。
分别以GPS单系统、GPS/BDS双系统、GPS/BDS/GLONASS 3系统以及GPS/BDS/GLONASS/Galileo 4系统这4种方案进行伪距差分解算,并将解算的结果与RTK结果对应历元进行比较,统计偏差。4种方案的偏差时间序列图如图 5所示。
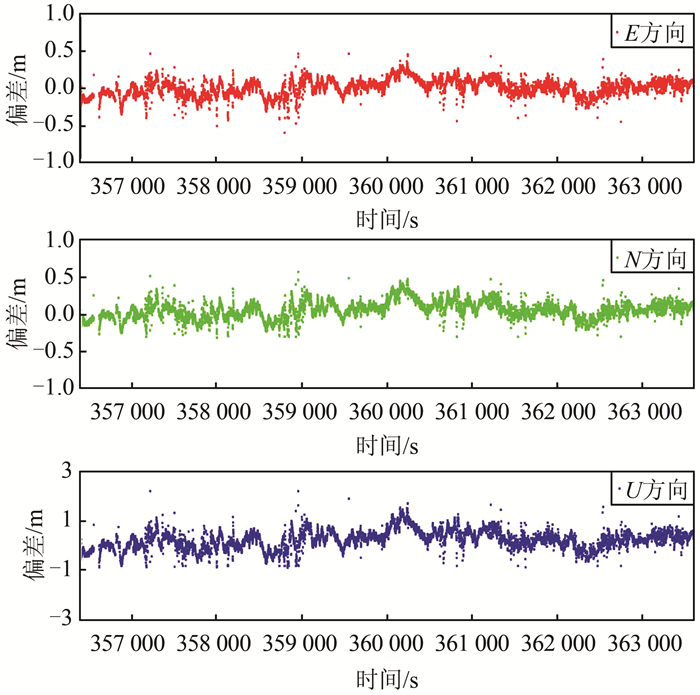 |
| 图 5 E、N和U方向偏差时间序列图 Fig.5 Bias Time Series of E, N and U for Four Systems of Kinematic Mode |
为进一步分析GPS/BDS/GLONASS/Galileo 4系统的伪距差分定位性能,统计4种解算方案的均方根(root mean square, RMS)、其相对于GPS单系统伪距差分的改进率和各解算方案最大偏差绝对值,如表 4所示。
| 表 4 动态4种解算方案RMS统计 Tab.4 RMS of Four Solutions of Kinematic Mode |
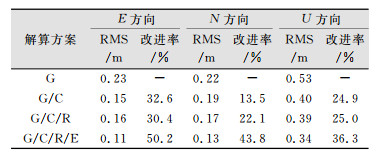 |
通过表 4可以看出,GPS/BDS/GLONASS/Galileo 4系统的伪距差分定位相对于GPS单系统的伪距差分定位,其E、N、U各分量分别提高了50.2%、43.8%、36.3%,可见GPS/BDS/GLONASS/Galileo 4系统的伪距差分定位的定位精度提高效果显著。
表 5给出了4种解算方案的在E、N、U 3个方向偏差的最大偏差绝对值。从表 5可以看出,4系统伪距差分定位相比于另外3种解算方案的最大偏差更接近参考值,这说明,多系统伪距差分相较于单系统伪距差分定位结果更加稳定。
| 表 5 各解算方案最大偏差绝对值/m Tab.5 Maximum Absolute Bias of Each Solution/m |
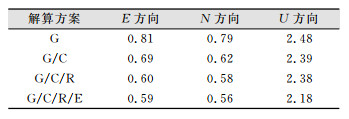 |
通过§2.1与§2.2中的解算及分析结果可以看出,多系统的伪距差分定位相较于单系统伪距差分定位有不同程度的提高。§2.1中静态数据的4系统伪距差分的偏差RMS的E、N、U分量分别为0.15 m、0.20 m、0.60 m;§2.2中动态数据的4系统伪距差分的偏差RMS的E、N、U分量分别为0.11 m、0.13 m、0.34 m。本文实验中的动态数据解算结果较静态数据更好,定位精度更高。这是因为:①选用的两个香港CORS站有近350 m的高差,而选用的动态数据流动站和基准站的高差几乎为0,这就使得动态数据中,流动站和基准站的空间相关误差几乎一致,伪距差分后可认为已完全消除,而静态数据中,由于高差的存在使得两个站的空间相关误差相差较大,从而伪距差分后仍有残留的对流层和电离层延迟误差;②静态数据中,流动站距基准站15.4 km,动态数据中,流动站与基准站的距离始终小于8 km,随着流动站距基准站距离变大,两站的空间相关误差的相关性降低,伪距差分后残余的空间相关误差就越大,从而伪距差分的精度降低。
3 结束语本文在简要给出GNSS差分定位算法的基础上,通过实测静态数据和车载动态数据对本文算法的正确性和差分定位性能进行了验证评估,可得到如下的具体结论。
1) 对静态和动态的伪距差分,多系统相较于单系统都有提升。静态伪距差分中,相较于GPS单系统伪距差分,多系统在水平方向通常有30%以上的提高,高程方向有12%以上的提高;动态伪距差分中,不同的多系统组合相较于单系统有着不同程度的提高,其中GPS/BDS/GLONASS/Galileo在水平方向提高可到40%以上,高程方向也能够达到36.33%。
2) 本文给出的差分定位算法是正确的,结果表明伪距平滑的GPS/BDS/GLONASS/Galileo 4系统伪距差分定位,在静态距基准站15 km,高差350 m时,水平方向RMS可达到0.3 m,竖直方向RMS可达0.7 m,在动态距基准站8 km以内时,水平方向RMS可达0.2 m,竖直方向RMS可达0.5 m。伪距差分的定位精度会随着离基准站的距离的增加而降低,对更远的静态或动态4系统伪距差分的精度有待进一步研究与分析。
| [1] |
邓健, 王庆, 潘树国, 等. 基于多参考站的分米级GPS伪距差分定位方法[J]. 东南大学学报(自然科学版), 2010, 40(2): 316-319. DOI:10.3969/j.issn.1001-0505.2010.02.019 |
| [2] |
李征航, 黄劲松. GPS测量与数据处理[M]. 武汉: 武汉大学出版社, 2010.
|
| [3] |
Liu Hui, Shu Bao, Xu Longwei, et al. Accounting for Inter-System Bias in DGNSS Positioning with GPS/GLONASS/BDS/Galileo[J]. Journal of Navigation, 2017, 70(4): 1-13. |
| [4] |
陈振. BDS/GPS网络伪距差分定位方法研究[D].北京: 中国测绘科学研究院, 2016
|
| [5] |
Kang Chuanli. A Differential Dynamic Positioning Algorithm Based on GPS/BeiDou[J]. Procedia Engineering, 2016, 137: 590-598. DOI:10.1016/j.proeng.2016.01.296 |
| [6] |
高星伟, 葛茂荣. GPS/GLONASS伪距差分的数据处理[J]. 测绘通报, 2000(6): 1-3. DOI:10.3969/j.issn.0494-0911.2000.06.001 |
| [7] |
Przestrzelski P, Bakula M, Galas R. The Integrated Use of GPS/GLONASS Observations in Network Code Differential Positioning[J]. GPS Solutions, 2016. |
| [8] |
周万振, 秘金钟, 李得海, 等. BDS/GPS/GLONASS融合网格伪距差分定位性能分析[J]. 测绘科学, 2016, 41(12): 5-9. |
| [9] |
Cai Changsheng, Gao Yang. A Combined GPS/GLONASS Navigation Algorithm for Use with Limited Sate-llite Visibility[J]. Journal of Navigation, 2009, 62(4): 671-685. DOI:10.1017/S0373463309990154 |
| [10] |
蒋军, 刘晖, 舒宝, 等. 基于RTCM2.x与RTCM3.x的两种伪距差分模式对比分析[J]. 测绘地理信息, 2018, 43(6): 58-61. |
| [11] |
尚梦云, 高晖, 常青, 等. GPS/GLONASS/BDS三系统组合定位的定权方法[J]. 太赫兹科学与电子信息学报, 2014, 12(3): 374-379. |
| [12] |
李灯熬, 吴刚, 赵菊敏, 等.BDS/GPS/GLONASS/GALILEO四系统组合定位方法研究[C].第六届中国卫星导航学术年会, 西安, 2015
|
| [13] |
谢翔, 喻小东, 郭际明, 等. 单频相位平滑伪距差分技术监测动态目标分析[J]. 测绘地理信息, 2013, 38(2): 14-16. |
 2019, Vol. 44
2019, Vol. 44

