| 地面摄影RTK辅助SFM算法的影像定向 |
地面影像的三维重建应用广泛(如交通事故勘查、地图等)。基于这些应用,影像定向精度和三维结构真实坐标和尺度十分重要。
运动恢复结构(structure from motion, SFM)算法是目前流行的影像定向方法,对影像数据要求低,成本比较低廉,受外部环境约束小,通用性好。SFM算法主要分为增量式SFM算法和全局式SFM算法两类。增量式SFM算法首先挑选两张影像作为“种子”开始重建,然后递增式逐张添加影像,估计影像位置姿态,要进行多次光束法平差,稳健性强,但是算法效率低,而且受累积误差的影响[1]。全局式SFM算法首先估计相对位姿,然后利用旋转平均[2]和平移平均恢复所有影像的全局位姿,最后进行一次光束法平差。该算法效率高,不受累积误差的影响,但是对外点极其敏感[3]。传统基于SFM算法的地面影像定向缺少位置姿态信息,无法恢复结构的绝对坐标和真实尺度。针对这一问题,地面摄影实时动态(real-time kinematic, RTK)可以采集影像位置姿态信息,然而由于RTK采集的坐标和角度与摄影测量定义不同,因此需要进行转换。heading pitch roll(HPR)和GPS转换摄影测量外方位元素通常有两种方法:①将像空间坐标系到物方坐标系的旋转矩阵分解到一系列中间坐标系中进行计算,然后将分解计算的所有旋转矩阵结合[4]。例如,刘军等[5]通过将旋转分解为“地辅坐标系-地心坐标系-导航坐标系-IMU坐标系-传感器坐标系-像空间坐标系”的连续坐标转换,求中间坐标系的旋转矩阵,然后将旋转矩阵顺序相乘。针对物方坐标系是投影坐标系的情况,袁修孝等[6]提出用补偿矩阵消除地球曲率和子午线偏差对角度变换的影响,并针对高斯投影推导了严密的角度补偿公式。②通过假设虚拟像点和物方点计算摄影测量角元素[7],该算法在笛卡尔坐标系和投影坐标系都适用。
本文考虑到地面影像定向的精度要求和恢复绝对位置和真实尺度的需要,提出地面摄影RTK辅助SFM算法的地面影像定向方法,以实时解算定向结果,恢复场景的绝对坐标和真实尺度。
1 地面摄影RTK工作原理 1.1 坐标系定义1)大地坐标系是以参考椭球面为基准建立起来的坐标系。地面点的位置用大地经度、大地纬度和大地高表示。
2)空间直角坐标系是以参考椭球体中心为原点,X轴指向本初子午线和赤道的交点,椭球体的旋转轴为Z轴,指向北为正,Y轴垂直于XOZ平面的右手坐标系。
3)北东天坐标系是原点位于载体中心,X轴指向北,Y轴指向东,Z轴指向参考椭球法线方向的左手坐标系。
4)物方坐标系是描述点在物方空间绝对坐标的坐标系,通常物方坐标系为平面投影加上高程系统或者为椭球切(割)面坐标系。
5) RTK坐标系是以RTK相位中心为原点,X轴指向RTK背面,Y轴指向右侧,Z轴指向上方的左手坐标系。
1.2 地面摄影RTK转角系统 1.2.1 HPR角度地面摄影RTK的姿态角为HPR转角系统,表示RTK坐标系到北东天坐标系的旋转角。绕X轴旋转的为横滚角,绕Y轴旋转的为俯仰角,绕Z轴旋转法的为航向角。
1.2.2 旋转矩阵1) RTK坐标系到北东天坐标系。北东天坐标系转到RTK坐标系经过以下3步:①北东天坐标系绕Z轴顺时针旋转航向角ψ;②绕第一次旋转后的Y轴逆时针旋转俯仰角θ;③绕第二次旋转后的X轴顺时针旋转横滚角ϕ。
旋转矩阵
| $ \begin{array}{c} \mathit{\boldsymbol{R}}_b^n = {\mathit{\boldsymbol{R}}_z}\left( \psi \right){\mathit{\boldsymbol{R}}_y}\left( \theta \right){\mathit{\boldsymbol{R}}_x}\left( \phi \right) = \left[ {\begin{array}{*{20}{c}} \begin{array}{c} \cos \psi \\ \sin \psi \\ 0 \end{array}&\begin{array}{c} - \sin \psi \\ \cos \psi \\ 0 \end{array}&\begin{array}{c} 0\\ 0\\ 1 \end{array} \end{array}} \right]\left[ {\begin{array}{*{20}{c}} \begin{array}{c} \cos \theta \\ 0\\ \sin \theta \end{array}&\begin{array}{c} 0\\ 1\\ 0 \end{array}&\begin{array}{c} - \sin \theta \\ 0\\ \cos \theta \end{array} \end{array}} \right]\left[ {\begin{array}{*{20}{c}} \begin{array}{c} 1\\ 0\\ 0 \end{array}&\begin{array}{c} 0\\ \cos \phi \\ \sin \phi \end{array}&\begin{array}{c} 0\\ - \sin \phi \\ \cos \phi \end{array} \end{array}} \right] = \\ \left[ {\begin{array}{*{20}{c}} \begin{array}{c} \cos \psi \cos \theta \\ \sin \psi \cos \theta \\ \sin \theta \end{array}&\begin{array}{c} - \sin \psi \cos \phi - \cos \psi \sin \theta \sin \phi \\ \cos \psi \cos \phi - \sin \psi \sin \theta \sin \phi \\ \cos \theta \sin \phi \end{array}&\begin{array}{c} \sin \psi \sin \phi - \cos \psi \sin \theta \cos \phi \\ - \cos \psi \sin \phi - \sin \psi \sin \theta \cos \phi \\ \cos \theta \cos \phi \end{array} \end{array}} \right] \end{array} $ | (1) |
式中,b表示RTK坐标系;n表示北东天坐标系。
2)北东天坐标系到空间直角坐标系。空间直角坐标系转到北东天坐标系经过3步:①空间直角坐标系绕其Z轴逆时针旋转l度;②绕第一次旋转后的Y轴顺时针旋转(90°+λ);③地心直角坐标系为右手系,而北东天坐标系为左手系,将第二次旋转后的Z轴反向。旋转矩阵为
| $ \mathit{\boldsymbol{R}}_n^e = \left[ {\begin{array}{*{20}{c}} \begin{array}{c} - \sin \lambda \cos l\\ - \sin \lambda \sin l\\ \cos \lambda \end{array}&\begin{array}{c} - \sin l\\ \cos l\\ 0 \end{array}&\begin{array}{c} \cos \lambda \cos l\\ \cos \lambda \sin l\\ \sin \lambda \end{array} \end{array}} \right] $ | (2) |
式中,e表示空间直角坐标系;λ、l分别是RTK相位中心的纬度和经度。
1.3 转换方法 1.3.1 角元素的计算取RTK坐标系下的4个点A、B、C、O,其中,O为RTK坐标系的原点。将大地坐标转置后赋值给
1)计算A、B、C、O在空间直角坐标系的坐标:
| $ \left\{ {\begin{array}{*{20}{l}} {{O_e} = f_g^e\left( {\begin{array}{*{20}{l}} {\lambda , }&{l, }&h \end{array}} \right)}\\ {{X_e} = \mathit{\boldsymbol{R}}_n^e\mathit{\boldsymbol{R}}_b^n{X_b} + {O_e}, \forall X \in \left\{ {A, B, C} \right\}} \end{array}} \right. $ | (3) |
式中,
2)计算A、B、C的大地坐标Xg:
| $ {X_g} = f_e^g\left( {{X_e}} \right), \forall X \in \left\{ {A, B, C} \right\} $ | (4) |
式中,
3)计算A、B、C、O在物方坐标系的坐标
① 物方坐标系为投影坐标系:
| $ {X_p} = f_g^p\left( {{X_g}} \right), \forall X \in \left\{ {A, B, C, O} \right\} $ | (5) |
式中,
② 物方坐标系为切(割)面直角坐标系:
| $ {X_p} = f_e^p\left( {{X_e}, {\lambda _0}, {l_0}, {h_0}} \right), \forall X \in \left\{ {A, B, C, O} \right\} $ | (6) |
式中,
4)计算RTK坐标系到物方坐标系的旋转矩阵
| $ \left\{ {\begin{array}{*{20}{l}} {\left[ {\begin{array}{*{20}{c}} {{\mathit{\boldsymbol{A}}_p} - {\mathit{\boldsymbol{O}}_p}}&{{\mathit{\boldsymbol{B}}_p} - {\mathit{\boldsymbol{O}}_p}}&{{\mathit{\boldsymbol{C}}_p} - {\mathit{\boldsymbol{O}}_p}} \end{array}} \right] = \mathit{\boldsymbol{R}}_b^p\left[ {\begin{array}{*{20}{c}} {{\mathit{\boldsymbol{A}}_b}}&{{\mathit{\boldsymbol{B}}_b}}&{{\mathit{\boldsymbol{C}}_b}} \end{array}} \right]}\\ {\mathit{\boldsymbol{R}}_b^p = \left[ {\begin{array}{*{20}{c}} {{\mathit{\boldsymbol{A}}_p} - {\mathit{\boldsymbol{O}}_p}}&{{\mathit{\boldsymbol{B}}_p} - {\mathit{\boldsymbol{O}}_p}}&{{\mathit{\boldsymbol{C}}_p} - {\mathit{\boldsymbol{O}}_p}} \end{array}} \right]{{\left[ {\begin{array}{*{20}{c}} {{\mathit{\boldsymbol{A}}_b}}&{{\mathit{\boldsymbol{B}}_b}}&{{\mathit{\boldsymbol{C}}_b}} \end{array}} \right]}^{ - 1}}} \end{array}} \right. $ | (7) |
式中,p表示物方坐标系。
5)计算像空间坐标系到物方坐标系的旋转矩阵:
| $ \mathit{\boldsymbol{R}}_c^p = \mathit{\boldsymbol{R}}_b^p\mathit{\boldsymbol{R}}_c^b $ | (8) |
式中,
影像投影中心和RTK相位中心存在偏差,影像投影中心在RTK坐标系的XOZ平面上,假设坐标为(dx, 0, dz),坐标值通过实际测量得到,线元素(Xs, Ys, Zs)通过计算公式如下:
| $ \left[ {\begin{array}{*{20}{c}} {{X_s}}\\ {{Y_s}}\\ {{Z_s}} \end{array}} \right] = \mathit{\boldsymbol{R}}_b^p\left[ {\begin{array}{*{20}{c}} {{\rm{d}}x}\\ 0\\ {{\rm{d}}z} \end{array}} \right] + {\mathit{\boldsymbol{O}}_p} $ | (9) |
SFM算法利用影像的相对位姿恢复影像的全局位姿和三维结构,分为3步:①利用匹配估计像对的相对位姿;②根据相对位姿恢复影像的全局位姿,利用三角定位计算物方点的坐标;③利用光束法平差[8]优化模型。通过RTK获取地面影像的位置姿态,便可得到地面影像的位置初值,结合全局式SFM算法估计影像的绝对位姿。RTK辅助SFM算法定向的步骤如下:
1)利用RTK采集数据。利用RTK采集坐标和HPR角度,根据角元素推导方法计算RTK坐标系到物方坐标系的旋转矩阵
2)进行尺度不变特征变换(scale-invariant fea‐ture transform, SIFT)和匹配,以及匹配点的粗差剔除。如果两张影像上匹配点对的数量大于等于50,则认为这两张影像构成一个像对,根据所有像对构建影像关系图G=(V, E),其中,V代表影像;E代表影像对,提取影像关系图的极大双边连通分量Gmax=(Vmax, Emax)。
3)估计像对的本质矩阵,分解本质矩阵得到像对的相对旋转矩阵。本质矩阵的计算采用5点算法配合稳健估计ACRANSAC(automatic random sam‐ple consensus)[9],本质矩阵分解可以得到4组结果,对每组结果都进行前方交会,计算所有的物方点,并统计在摄像机前方的物方点数量,设4组结果在摄像机前方的物方点数量最大值为M,次大值为m,当m与M的比值小于0.7时,选择数量值最大的结果作为正确结果。
4)剔除错误的相对旋转矩阵。由本质矩阵分解的相对旋转矩阵存在粗差,需要进行粗差剔除。搜索影像中所有构成闭合环的三元组
| $ \Delta \mathit{\boldsymbol{R}} = {\cos ^{ - 1}}\left( {\frac{1}{2}{\rm{tr}}\left( {\begin{array}{*{20}{c}} {{\mathit{\boldsymbol{R}}_{ki}}}&{{\mathit{\boldsymbol{R}}_{ij}}}&{{\mathit{\boldsymbol{R}}_{jk}}} \end{array}} \right) - 1} \right) $ | (10) |
式中,tr表示求矩阵的迹。
当∆R大于5°时,则删除该三元组,然后根据保留的相对旋转关系重新构建影像关系图,并提取影像关系图的极大双边连通分量Gr=(Vr, Er)。
5)恢复全局旋转矩阵R。相对旋转矩阵和全局旋转矩阵的约束关系为:
| $ \left\{ {\begin{array}{*{20}{l}} {{\mathit{\boldsymbol{R}}_j} = {\mathit{\boldsymbol{R}}_{ij}}{\mathit{\boldsymbol{R}}_i}, \left( {i, j} \right) \in {E_r}}\\ {{\mathit{\boldsymbol{R}}_i}{\mathit{\boldsymbol{R}}_i}^{\rm{T}} = 1, \left| {{\mathit{\boldsymbol{R}}_i}} \right| = 1, i \in {V_r}} \end{array}} \right. $ | (11) |
式(11)的约束方程可以通过最小二乘求解,并通过奇异值分解(singular value decomposition, SVD)得到满足正交约束的旋转矩阵。
6)计算相对平移向量t。利用三视图最小化重投影误差的约束估计t,首先寻找所有已知姿态的影像中两两互为匹配对的三视图(i, j, k),三视图重投影误差为:
| $ \rho \left( {{\mathit{\boldsymbol{t}}_i}, {\mathit{\boldsymbol{X}}_p}} \right) = \left\| {\left( {\mathit{\boldsymbol{x}}_p^i - \frac{{\mathit{\boldsymbol{R}}_i^1{\mathit{\boldsymbol{X}}_p} + \mathit{\boldsymbol{t}}_i^1}}{{\mathit{\boldsymbol{R}}_i^3{\mathit{\boldsymbol{X}}_p} + \mathit{\boldsymbol{t}}_i^3}}, \mathit{\boldsymbol{y}}_p^i - \frac{{\mathit{\boldsymbol{R}}_i^2{\mathit{\boldsymbol{X}}_p} + \mathit{\boldsymbol{t}}_i^2}}{{\mathit{\boldsymbol{R}}_i^3{\mathit{\boldsymbol{X}}_p} + \mathit{\boldsymbol{t}}_i^3}}} \right)} \right\| $ | (12) |
式中,R、t的上标表示矩阵的行,在t1=[0 0 0]的约束下利用线性规划求解式(12)的最小L∞范数解。
然后利用全局旋转矩阵和局部平移向量计算两两视图的相对平移向量,同时更新相对旋转矩阵。
7)恢复全局平移向量T。考虑相对平移向量的尺度统一问题,影像相对位姿和全局平移向量应该满足如下方程:
| $ \left\| {{T_j} - {\mathit{\boldsymbol{R}}_{ij}}{T_i} - {\lambda _{ij}}{\mathit{\boldsymbol{t}}_{ij}}} \right\| = 0, \forall i, j $ | (13) |
把式(13)化为最小化L∞范数的问题,利用线性规划求解。
8)计算所有物方点的三维坐标。首先利用并查集算法[10]串点,然后通过三角定位算法计算物方点。
9)利用RTK和SFM算法分别计算的影像位置求解七参数,通过七参数转换把影像的位姿和物方点转到绝对坐标系下。
10)光束法平差整体优化。
3 实验及分析本文采用地面摄影RTK采集的影像、GPS和HPR角度作为实验数据,分两组进行实验:①推算影像角元素,计算RTK地面点的坐标,验证转换公式;② RTK辅助SFM算法定向。经过实际测量,RTK杆高1.666 7 m,影像投影中心在RTK坐标系中的坐标为(0.017, 0, -0.236 2)m。
3.1 实验1:计算影像角元素和RTK地面点坐标 3.1.1 实验数据和方法1)推算影像角元素。利用RTK在任意位置上采集一组影像,根据本文角元素计算方法推算影像的角元素,角元素采用3×3矩阵表示或3个角度值Omega Phi Kappa(OPK)。假定Smart3D计算的角元素为真值,计算角元素真值与估计值的差值。实验1像空间坐标系定义X轴指向图像右侧,Y轴指向图像底部,Z轴指向相机前方,忽略RTK坐标系和像空间坐标系的角度误差,则像空间坐标系到RTK坐标系的旋转矩阵
| $ \mathit{\boldsymbol{R}}_c^b = \left[ {\begin{array}{*{20}{c}} \begin{array}{l} 0\\ 1\\ 0 \end{array}&\begin{array}{l} 0\\ 0\\ - 1 \end{array}&\begin{array}{l} 1\\ 0\\ 0 \end{array} \end{array}} \right] $ | (14) |
2)计算RTK地面点坐标。RTK放置在一已知坐标的地面点上,将RTK朝不同方向,倾斜不同角度采集几组影像,地面点在RTK坐标系中的坐标为(0.017, 0, -0.236 2)m,根据线元素计算公式推算地面点的坐标,计算坐标真值与估计值的差值。
3.1.2 实验结果和分析表 1记录的是Smart3D计算的角元素和利用RTK推算的角元素分别在OPK 3个角度上的差值,差值集中在1°~4°。表 2记录的是地面点坐标真值与不同倾斜角度下的计算值的坐标差,差值在2 cm左右。倾斜改正有精度损失,所以垂直改正的精度较高,从表 2可以看出,点1和点2的首行坐标差值是垂直观测的结果。由于本实验的角元素“真值”为Smart3D计算的结果,而实验中Smart3D是将影像内参、外参、畸变参数一起优化计算的,所以角元素的结果受其他参数的影响。考虑到角元素“真值”的误差,RTK坐标系和像空间坐标系的安装角度误差以及RTK原始数据的误差等多种因素对实验结果的影响,本文认为该实验结果足以验证转换公式的正确性。
| 表 1 角元素角度差 Tab.1 Angle Difference of Angular Elements |
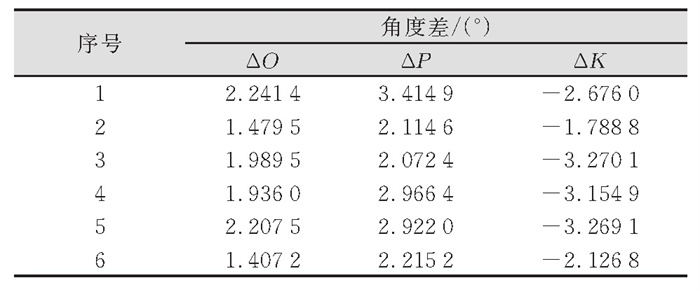 |
| 表 2 地面点真值和计算值坐标差 Tab.2 Difference Between True and Calculated Coordinates of Ground Points |
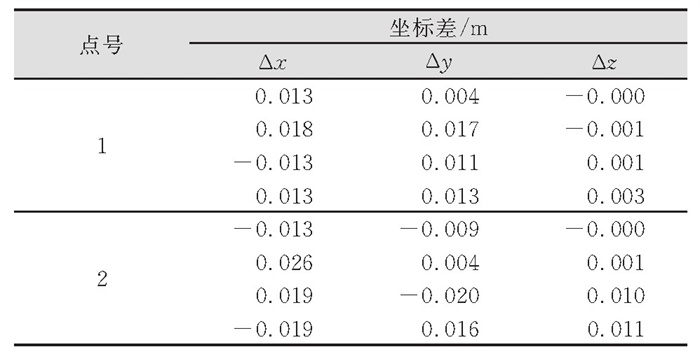 |
3.2 实验2:RTK辅助的SFM算法定向 3.2.1 实验数据和方法
利用RTK采集30张影像作为实验数据,摄影焦距为20 mm,拍摄平均距离约13 m。利用转换公式计算影像投影中心坐标,辅助SFM算法进行影像定向。为检验该方法可行性,将其与Smart3D软件的定向结果进行对比,并提供3个控制点和3个检查点进行精度评价,保证SFM算法和Smart3D的外部约束条件相同。
3.2.2 实验结果和分析表 3为控制点和检查点的物方中误差统计结果,可以看出,两种方法的控制点物方中误差均在mm级,检查点物方中误差均在5 cm内。图 1为控制点和检查点重投影误差的统计结果,P1、P2、P3代表控制点,H1、H2、H3代表检查点。如图 1所示,RTK辅助SFM定向方法控制点重投影误差低于1个像素,检查点重投影误差低于2.5个像素。结果表明,RTK辅助SFM定向方法可以达到Smart3D同等精度。
| 表 3 控制点和检查点物方中误差/m Tab.3 Mean Square Errors of the Object Space Coordi‐nates of Control Points and Check Points/m |
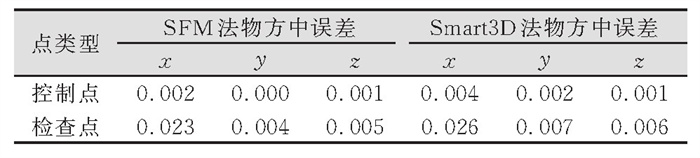 |
 |
| 图 1 控制点检查点重投影误差 Fig.1 Reprojection Errors of Control Points and Check Points |
4 结束语
本文推导了地面摄影RTK计算影像外方位元素的公式,并提出地面摄影RTK辅助SFM算法的影像定向方法。相对于地面控制点,地面摄影RTK可以实时获取影像的初始外方位元素,实现实时相片解算和三维坐标的获取,无需或只需少量控制点就能获得场景的绝对坐标和真实尺度。实验结果表明,本文利用GPS和HPR计算外方位元素的公式正确,利用RTK辅助SFM算法的影像定向方法可以得到精确的具有地理坐标和真实尺度的定向结果。
| [1] |
Moulon P, Monasse P, Marlet R. Adaptive Structure from Motion with a Contrario Model Estimation[C]. 2013 Asian Conference on Computer Vision, Daejeon, Korea, 2013.
|
| [2] |
Chatterjee A, Govindu V M. Efficient and Robust Large-Scale Rotation Averaging[C]. 2013 IEEE International Conference on Computer Vision, Sydney, Australia, 2013.
|
| [3] |
Wilson K, Snavely N. Robust Global Translations with 1DSfM[C]. 2014 European Conference on Computer Vision, Zurich, Switzerland, 2014.
|
| [4] |
Bäumker M, Heimes F J. New Calibration and Computing Method for Direct Georeferencing of Image and Scanner Data Using the Positiong and Angular Data of an Hybrid Inertial Navigation System[J]. Proceedings of the National Academy of Science of the United States of America, 2001, 43: 197-212. |
| [5] |
GPS/INS系统HPR与OPK角元素的剖析与转换[J]. 测绘科学, 2006, 31(5): 54-56. |
| [6] |
高斯-克吕格投影坐标系下POS角元素的转换方法[J]. 测绘学报, 2011, 40(3): 338-344. |
| [7] |
Zhao H T, Zhang B, Wu C S, et al. Development of a Coordinate Transformation Method for Direct Georeferencing in Map Projection Frames[J]. ISPRS Journal of Photogrammetry and Remote Sensing, 2013, 77: 94-103. DOI:10.1016/j.isprsjprs.2012.12.004 |
| [8] |
光束法平差简史与概要[J]. 武汉大学学报·信息科学版, 2018, 43(12): 1 797-1 810. |
| [9] |
Moisan L, Moulon P, Monasse P. Automatic Homographic Registration of a Pair of Images, with a Contrario Elimination of Outliers[J]. Image Processing on Line, 2012, 2: 56-73. DOI:10.5201/ipol.2012.mmm-oh |
| [10] |
Moulon P, Monasse P. Unordered Feature Tracking Made Fast and Easy[C]. The 9th Eupropean Conference on Visual Media Production, London, UK, 2012.
|
 2021, Vol. 46
2021, Vol. 46

