| 雷达探测范围地形可视域分析方法 | [PDF全文] |
雷达的探测范围受两方面的影响,一是雷达的发射功率等;二是地形、大气等雷达周围环境的作用[1]。如何高效展示雷达探测范围以及大气环境、复杂地形等复杂环境因素对雷达探测性能的影响,是复杂环境下雷达性能分析和计算电磁学的重要研究内容之一[2]。
目前,获取雷达探测范围的有效途径一般采用复杂地形条件和大气环境下的可视域分析方法,这需要建立正确合理的雷达探测范围可视域分析模型,为快速、真实、准确地绘制出雷达探测范围提供重要的手段。本文引入了等效地球半径[3],有效化简了复杂大气环境下的雷达探测范围地形可视域分析模型,并进行了算法实现和性能分析。
1 地形可视域分析原理及模型 1.1 可视域分析基本原理地形可视域分析采用的地形基础数据是数字高程模型(digital elevation model, DEM)数据。通过两点之间的可视性分析计算,以观察点为基点,沿着待分析路径逐点检查观察点至目标点的可视性分析[4]。
如图 1,在仅考虑地形条件下,结合数字高程模型DEM进行分析,以某一方向为观察方向,观察点为点A,视线分别为AB、AC,分别与剖面1和剖面2交于点O和点P,其中点O的高度层为L1,点P的高度层为L2,由图 1可知,阴影区域a和b不可视。
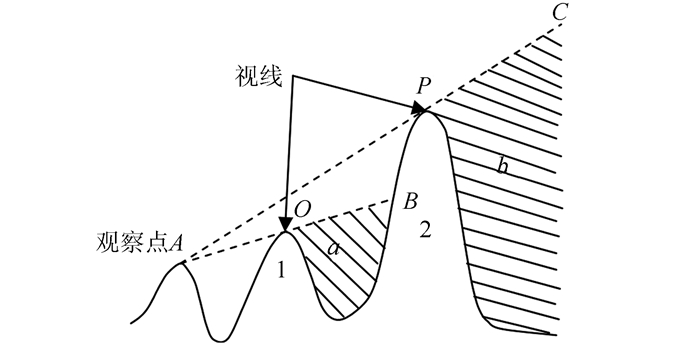 |
| 图 1 地形剖面 Fig.1 Topographical Profile Graph |
1.2 雷达探测范围数学模型
可视域分析算法的研究虽然基于两点之间的通视分析,但是忽略了大范围特别是无线电波在大气层中产生的折射影响,因此根据相关专业在电磁波覆盖范围等分析中的主要做法,为顾及无线电波在空气中传播折射的影响而引入等效地球半径[3]。
以雷达探测飞机为例进行可视域分析,假设地球为均匀球体,飞机距雷达距离为S机,障碍物距雷达距离为S障,飞机高度为H机,障碍物高度为H障,雷达高度为H雷。等效地球半径为R地,地心角为α,雷达与切点的角度为α切,雷达与障碍物角度为α障,雷达与飞机角度为α机。β为雷达顶端的角度,雷达到障碍物与雷达到地心连线之间夹角为β障。如图 2所示。
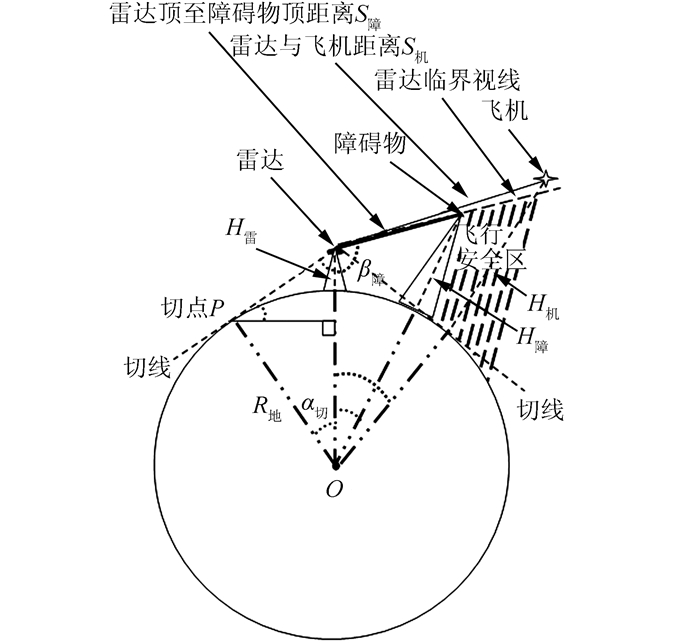 |
| 图 2 基于等效地球半径的雷达通视原理图 Fig.2 Radarvisibility Schematic Based on Equivalent Earth Radius |
若不考虑地形因素,等效地球半径为R地,雷达对某一高度层的理论最大探测距离为S探,则可将图 2简化为图 3。
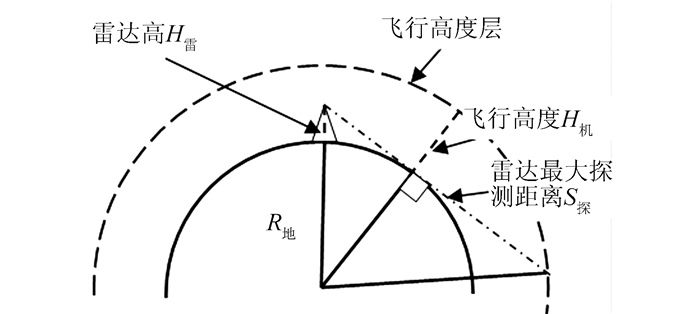 |
| 图 3 不考虑地形起伏情况的雷达通视性 Fig.3 Radar Visibility Without Considering Terrain Fluctuation |
由图 3可知:
| $ \begin{array}{l} {S_探} = {\left( {{{\left( {{R_地} + {H_雷}} \right)}^2}-R_地^2} \right)^{\frac{1}{2}}} + \\ \;\;\;{\left( {{{\left( {{R_地} + {H_机}} \right)}^2}-R_地^2} \right)^{\frac{1}{2}}} \end{array} $ |
在此条件下,其他方向的最大探测距离也等于S探,雷达的可视范围(即探测区范围)在二维平面上就是一个以雷达位置为圆心,以S探为半径的圆形范围,如图 4所示。
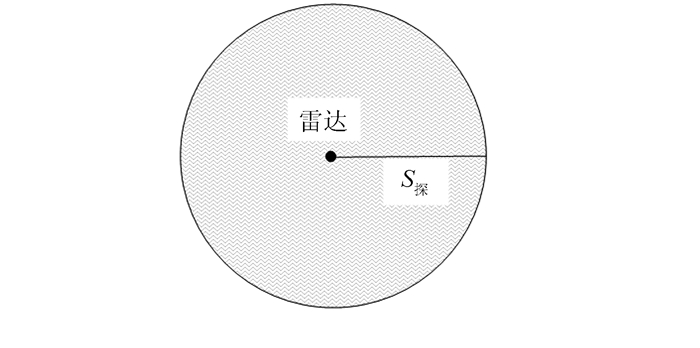 |
| 图 4 不考虑地形起伏情况的雷达探测范围 Fig.4 Radar Detection Range Without Considering Terrain Fluctuation |
当飞机在此高度层飞行时,与雷达的距离S≤S探时,即进入雷达探测区范围,就会被雷达发现。而实际的地形条件复杂多样,当考虑到地形条件的影响时,如有障碍物(高为H障,与雷达距离为S障),雷达的探测距离就会大大缩短,如图 5所示。
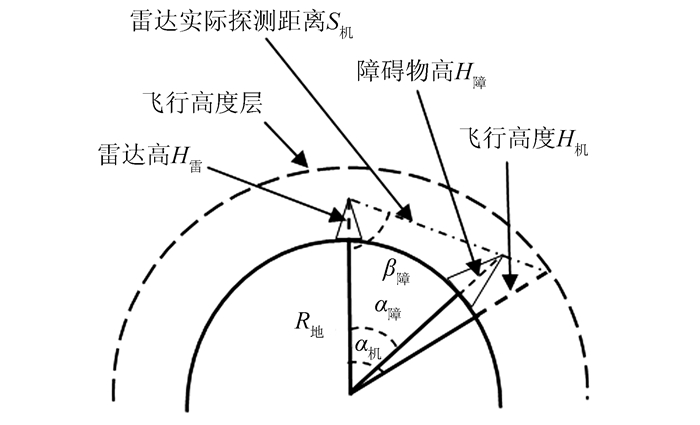 |
| 图 5 考虑简单地形起伏情况的雷达通视性 Fig.5 Radar Visibility Considering Simple Terrain Fluctuation |
由图 4计算可得到雷达探测距离计算公式,其中π取值3.141 592 6,则有:
| $ \begin{array}{l} {\beta _障} = \arccos \left( {\frac{{\left( {{{\left( {{R_地} + {H_雷}} \right)}^2} + S_障^2-{{\left( {{R_地} + {H_障}} \right)}^2}} \right)}}{{2 \times {S_障} \times \left( {{R_地} + {H_雷}} \right)}}} \right)\\ {\alpha _机} = \pi-{\beta _障}-\arccos \left( {\sin \left( {{\beta _障}} \right) \times \frac{{{R_地} + {H_雷}}}{{{R_地} + {H_机}}}} \right)\\ {S_机} = {\left( {{\left( {{R_地} + {H_雷}} \right)}^2} + {{\left( {{R_地} + {H_机}} \right)}^2-}\right.}\\ {\left.{ 2 \times \left( {{R_地} + {H_雷}} \right) \times \left( {{R_地} + {H_机}} \right) \times \cos \left( {{\alpha _机}} \right)} \right)^{\frac{1}{2}}} \end{array} $ |
由此可得,在某一方向的障碍物影响下,雷达的临界探测距离为S机。当飞机与雷达的距离S>S机时,飞机处于安全区,反之,则飞机被雷达发现。
然而,在实际情况下,飞机与雷达之间的地形条件可能会非常复杂,会出现不同情况的障碍物,如图 6所示。
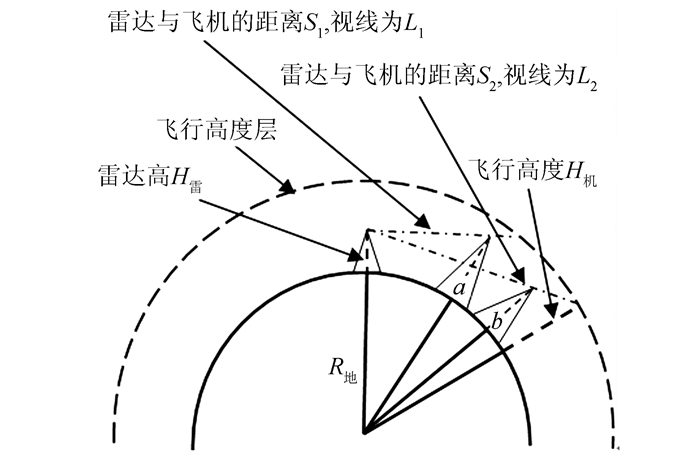 |
| 图 6 考虑复杂地形情况的雷达通视性 Fig.6 Radar Visibility Considering Complex Terrain Fluctuation |
在某一方向上存在障碍物a和b,当飞机与雷达的距离S < S1时,飞机会被雷达探测到;当飞机与雷达的距离S1 < S < S2, 飞机处于视线L1与L2之间时,由于被障碍物a所遮挡而不会被发现,因此,在此情况下雷达的临界探测距离为S1。
当在雷达的某一探测方向上出现多个障碍物时,雷达的临界探测距离实际就是雷达与飞机之间的最短可视距离(也就是斜率最大的探测视线长度),这一长度值也是雷达能够探测到飞机的最大探测距离,此长度必然小于或等于(无障碍物情况)理论最大探测距离S探。
同理,可以计算出其他方向的最短距离S,构成一个不规则雷达威胁区的探测范围,如图 7所示。
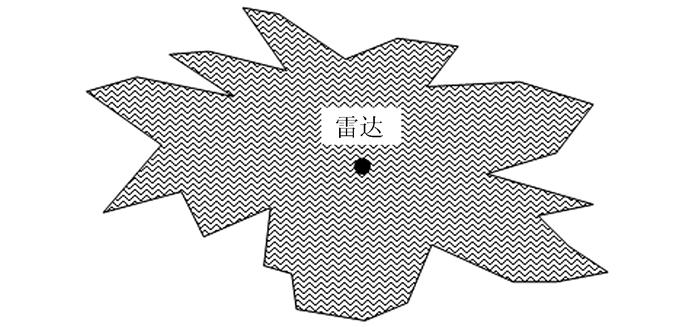 |
| 图 7 基于实际地形的雷达探测范围 Fig.7 Radar Detection Range Based on Real Terrain |
2 地形可视域算法设计与实现
本文研究的雷达探测区是指雷达的平面探测范围。其基本原理是建立在地理空间地形分析基础上的可视域分析方法[5-10],计算雷达在同一高度层各个方位的最大探测距离,然后再将该高度层各个方位的最大探测距离点连成一条闭合曲线,从而得到该高度层的雷达平面探测范围。
以某一地区DEM数据作为地理信息分析基础数据,根据基于地形分析的雷达低空探测区可视域分析原理以及理论模型,为雷达探测区范围计算设计合理有效的算法。
1) 设定雷达可视域分析高度层h(如1 000 m);
2) 确定雷达位置,获取雷达位置坐标(X, Y);
3) 计算该雷达理论最大探测距离S探;
4) 以雷达为中心点,以某一方向为起始方向计算该方向上雷达的最大探测距离。
① 以中心点为起始点,在该方向上每隔一定步长L(如100 m)为间隔取点,并通过DEM数据分析获取该点的高程值(即障碍物高度);
② 计算每一个障碍物到分析高度层的通视距离;
③ 对该方向上所有通视距离进行比较,获取最小值S;
④ 验证该最小值S,若满足S≤S探,则该方向的雷达最大探测距离为S,否则为S探,最后得到该方向的雷达实际最大探测距离S。
⑤ 沿着起始方向,每隔一定角度间隔γ(如1′)选取一个探测方向进行计算,获取该方向上的雷达实际最大探测距离S,计算该最大距离探测点的位置坐标(X0,Y0);
⑥ 获取各个方向上的实际最大探测距离S,分别计算该最大距离探测点的坐标(Xn,Yn);
⑦ 将各个方向上的最大距离探测点连成一条闭合曲线来形成一个闭合面,即得到该雷达的探测区范围。
3 地形可视域算法性能分析利用§2算法进行可视域分析时,分析结果的精度受到诸多条件的影响[11-20],比如DEM基础数据的分辨率和精度、步长和间隔角度的参数取值。理论上,DEM数据的分辨率和精度越高,分析步长和间隔角度越小,得到的分析结果越接近雷达实际探测范围,但是分析的时间也会变长。因此需要综合考虑需求进行可视域分析。
对1 000 m高度层,选用不同参数进行分析,其中步长为L,间隔角度为α:①步长500 m,间隔角度为10′;②步长100 m,间隔角度为1′;③步长30 m,间隔角度为1′。
通过分析,图 8为L=500 m,α=10′时可视域分析结果;图 9为L=100 m,α=1′时可视域分析结果;图 10为L=30 m,α=1′时可视域分析结果。
 |
| 图 8 当L=500 m,α=10′时可视域分析结果 Fig.8 Results of Visibility Analysis when L=500 m and α=10′ |
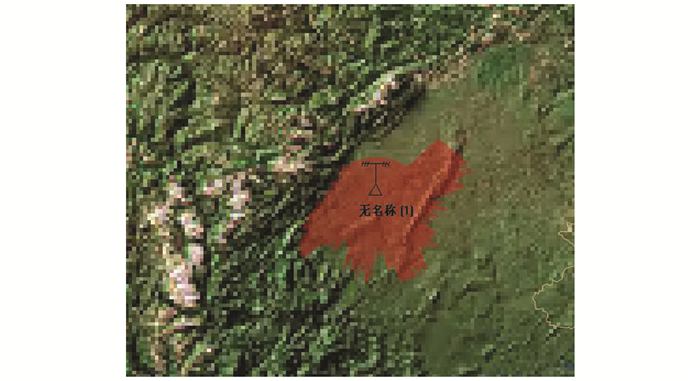 |
| 图 9 当L=100 m,α=1′时可视域分析结果 Fig.9 Results of Visibility Analysis when L=100 m and α=1′ |
 |
| 图 10 当L=30 m,α=1′时可视域分析结果 Fig.10 Results of Visibility Analysis when L=30 m and α=1′ |
通过对比,当分析步长和间隔角度小时,所得到的雷达探测范围也小。据每一个扫描方向最终获取得是该方向上可视线长度最小(即可视线斜率最大)的障碍物可视距离,并以此作为该方向上雷达所能探测到的最大距离的原则来分析可知,则障碍物取的越多,所获取的DEM高程点数据越密集,雷达探测范围应该越小,当参数值小到一定程度(与DEM数据的精度和分辨率相关),雷达的探测区范围变化会越来越小,趋于某一稳定范围,该范围则最接近雷达实际探测范围。因此,可视域分析算法具有一定的实用性,在一定程度上正确地反映了雷达在复杂地形条件下探测区范围。
4 结束语本文提出了一种基于等效地球半径的雷达探测范围地形可视域模型分析方法,它是建立在地形可视域分析原理基础上的一种雷达可视域分析方法,并详尽阐述了该方法的基本原理和可视域分析数学模型建立的过程,然后根据其原理和模型设计了相应的算法并进行了实现,结果更加真实地反映了雷达在实际情况下的探测效果,能够为雷达网络优化部署等提供重要依据。
| [1] |
周鹏.复杂地形下雷达探测威力图的仿真算法及可视化研究[D].上海: 上海交通大学, 2013 http://www.docin.com/p-1205850512.html
|
| [2] |
白玉兵.复杂环境下雷达探测范围可视化研究[D].长沙: 湖南大学, 2013 https://www.doc88.com/p-1691941287014.html
|
| [3] |
刘少毅, 张卫柱, 赵永刚, 等. 基于等效地球半径和地形的电磁波覆盖范围分析[J]. 测绘科学, 2015, 40(5): 29-32. |
| [4] |
周丹.基于GIS可视域分析的矿山环境视觉污染评价[D].南京: 南京大学, 2011 http://cdmd.cnki.com.cn/Article/CDMD-10284-1011126806.htm
|
| [5] |
孙涛, 谢晓方, 孙永芹. RSG地形的矢量视域改进算法[J]. 计算机工程与应用, 2010, 46(28): 160-162. |
| [6] |
徐健, 蔡忠亮, 赵军, 等. 以自我为中心的电子地图空间信息组织与可视化[J]. 测绘地理信息, 2017, 42(1): 73-77. |
| [7] |
靳海亮, 李留磊, 袁松鹤, 等. 一种用于三维城市建筑物的可视域分析算法[J]. 测绘通报, 2018(1): 103-106. |
| [8] |
刘子轩, 艾廷华. 自适应显示环境可视化表达的线要素图形化简[J]. 测绘地理信息, 2017, 42(1): 78-82. |
| [9] |
沈笑云, 曹博, 张思远, 等. 开阔区域ADS-B地面站信号覆盖仿真分析[J]. 计算机仿真, 2015, 32(3): 94-99. DOI:10.3969/j.issn.1006-9348.2015.03.021 |
| [10] |
封瑜. 甚高频覆盖范围研究与仿真计算[J]. 青海师范大学学报(自科版), 2017, 33(3): 30-36. |
| [11] |
王栋, 刘林, 张顺发, 等. 基于SRTM高程数据的变步长海面快速可视域分析方法[J]. 指挥控制与仿真, 2017, 39(4): 117-120. DOI:10.3969/j.issn.1673-3819.2017.04.025 |
| [12] |
周宏宇, 李朝阳. 低空地空通信覆盖分析与仿真[J]. 信息通信, 2017(3): 171-172. DOI:10.3969/j.issn.1673-1131.2017.03.091 |
| [13] |
杨坤.可视域分析算法的并行化与容错研究[D].南京: 南京师范大学, 2014
|
| [14] |
鲁旭虎. 二次雷达信号连续覆盖需求和可靠性分析[J]. 空中交通, 2015(2): 49-51. |
| [15] |
丁一, 江崇波, 苑克磊, 等. 基于GIS通视分析的长岛海域溢油陆岸监测系统选址——以大黑山为例[J]. 广西科学院学报, 2016, 32(2): 88-91. DOI:10.3969/j.issn.1002-7378.2016.02.004 |
| [16] |
尹长林, 许文强. 基于3DGIS的城市规划可视性分析模型研究[J]. 测绘科学, 2011, 36(4): 142-144. |
| [17] |
熊皓, 王爱玲. 关于等效地球半径的概念和定义问题[J]. 电波科学学报, 1997, 12(1): 10-14. |
| [18] |
刘伟, 戴浩. 有源干扰条件下雷达探测范围通视分析模型的MapX仿真方法[J]. 军事运筹与系统工程, 2007, 21(1): 41-45. DOI:10.3969/j.issn.1672-8211.2007.01.009 |
| [19] |
王树文. 计算机模拟雷达网平面探测范围的一种绘制方法[J]. 空军雷达学院学报, 1999, 13(3): 51-53. |
| [20] |
吕智. 地球球面和大气折射对气象雷达目标探测的影响[J]. 现代电子技术, 2012, 35(12): 119-122. DOI:10.3969/j.issn.1004-373X.2012.12.040 |
 2019, Vol. 44
2019, Vol. 44

