| 基于CATS软件的连续运行参考站噪声分析 |
2. 深圳市地籍测绘大队, 广东 深圳, 518034
2. Shenzhen Cadastral Surveying and Mapping Office, Shenzhen 518034, China
近20余年来, 国际GNSS服务组织(International Global Navigation Satellite System Service, IGS)基准站以及各等级连续运行参考站(continuously operating reference stations, CORS)积累的GPS观测数据为大地测量学和地球动力学研究提供了宝贵的数据基础。研究基准站坐标时间序列特征不仅有助于了解各种地球物理现象对基准站位置的影响规律, 而且可以对各种误差模型进行修改, 进一步提高基准站位置精度[1]。
事实上, GPS观测数据中普遍存在各类噪声, 包括与时间无关的白噪声和包括与时间无关的白噪声和与时间相关的有色噪声[2-5]。经数据处理后, 这些噪声会传递到坐标时间序列中。Nilolaidis[6]分析了全球许多GPS基准站后认为坐标时间序列的噪声更接近于白噪声和闪烁噪声的叠加。由于忽略了这一点, 通常基于白噪声假定得到的速率估计结果存在一定偏差[7], 尤其在地质条件和板块运动较为稳定的地区, 由于GPS位移量很小, 若低估观测噪声的误差影响将会导致地壳形变大小甚至方向上出现错误。因此, 考虑有色噪声的影响显得格外重要。本文基于深圳市5个CORS站近6年观测数据, 来确定最优噪声模型。
1 GPS坐标时间序列的噪声分析方法本文利用武汉大学自主开发的PANDA软件, 基于非差数据处理策略解算2010~2015年深圳CORS参考站观测数据, 解算获得各参考站单日解坐标时间序列。图 1为石岩站坐标时间序列。从图 1中可以看出, 南北分量、东西分量线性趋势较为明显, 而垂直分量上则呈现出较为明显的年周期性。
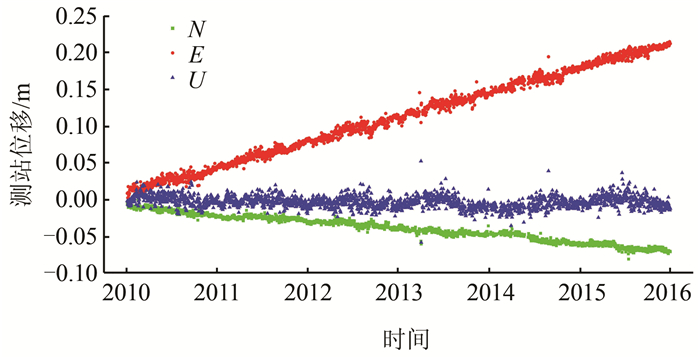 |
| 图 1 石岩站坐标时间序列 Fig.1 Coordinate Time Series of SZSY Station |
1.1 各站坐标分量的单日序列函数模型
为了分析参考站坐标时间序列中的线性项、周期项以及噪声项, 对各站坐标分量的单日解序列建立函数模型[6]为:
| $ \begin{array}{l} y\left( {{t_i}} \right) = a + b{t_i} + c{\rm{sin}}\left( {2{\rm{ \mathsf{ π} }}{t_i}} \right) + d{\rm{cos}}\left( {2{\rm{ \mathsf{ π} }}{t_i}} \right) + e{\rm{sin}}\left( {4{\rm{ \mathsf{ π} }}{t_i}} \right) + f{\rm{cos}}\left( {4\pi {t_i}} \right)\\ + \sum\limits_{{\rm{ }}j = 1}^{{n_i}} {{g_i}H\left( {{t_i} - {T_{hj}}} \right)} + \sum\limits_{j = 1}^{{n_h}} {{h_i}H\left( {{t_i} - {T_{hj}}} \right){t_i}} + \sum\limits_{j = 1}^{{n_k}} {{k_i}{\rm{exp}}\;} {\rm{ }}\left( { - \frac{{\left( {{t_i} - {T_{hj}}} \right){t_i}}}{{{\tau _j}}}} \right) \times \\ H\left( {{t_i} - {T_{hj}}} \right) + {v_i} \end{array} $ | (1) |
式中, ti(i=1, …, N)为以年为单位的时间; 待定系数a为序列线性项的截距; b为线性速率; c、d和e、f分别为年周期和半年周期项的系数; gi表示由于各种原因引起的阶跃式坐标突变(如远场大地震引起的同震位移等); H为阶跃函数, 这里假定发生这种突变的时间Thj是已知的, 在此时刻之前H的值为0, 在此时刻之后H的值为1;后面两项是用来描述某时刻发生的突变事件对测站运动速率的改变, 使用于更复杂、更精准的情况; vi为残差值, 代表观测值与拟合值间的差异, 即本文将要分析的噪声信号。利用该参数模型可以有效地估计参考站时间序列季节性变化, 同时也能明显地反映连续参考站的位置和速度信息。
由于研究对象是与地壳形变无关的噪声信息, 所以对于各参考站坐标时间序列都必须按照式(1)扣除线性项、周期项以及各种原因造成的偏移量。可以运用统计软件SPSS或时间序列分析软件CATS拟合出式(1)中系数a~f, 将坐标时间序列扣除已知项, 得到如图 2所示的残差序列, 进而对噪声特性进行分析。从图 2可以看出, 扣除了线性项、周期项和阶跃项后的的残差序列表现稳定, N、E方向的残差范围均在1 cm以内, 而U方向残差变化范围相对较大。频谱分析法和最大似然估计法是两种常用的噪声分析方法。
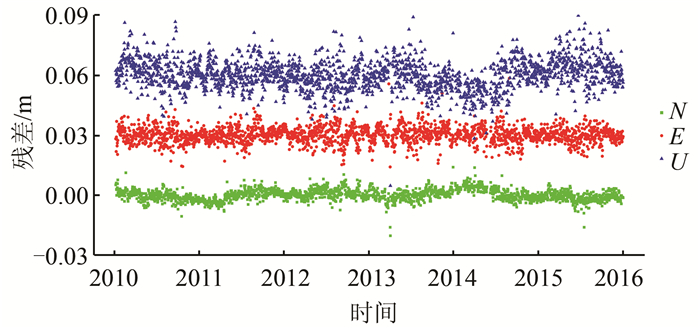 |
| 图 2 石岩站NEU分量残差序列 Fig.2 Residual Series of SZSY Station |
1.2 频谱分析法
自然界中许多现象的噪声具有幂律性质, 即噪声功率谱密度P(f)与它对应的噪声频率f之间存在某种幂次关系:
| $ P{\rm{ }}f{\rm{ }} = {P_0}{f^\alpha } $ | (2) |
等式两边取对数有:
| $ {\rm{ln}}P\left( f \right){\rm{ }} = {\rm{ln}}{P_0} + \alpha {\rm{ln}}f $ | (3) |
式中, P(f)为功率谱密度, f为该类噪声的频率; P0和α是待定参数。由式(3)可以看出, 谱指数α是功率谱密度P(f)对噪声频率f分布图的斜率。对噪声来说, 不同的谱指数对应不同的噪声特性。若α=0, 则对应的是白噪声; 若α=-1, 则对应的是闪烁噪声; 若α=-2, 则对应的是随机游走噪声[8]。因此, 求出功率谱密度和谱指数是确定噪声性质的关键。
1.3 最大似然估计法最大似然估计(maximum likelihood estimation, MLE)是一种非线性的最小二乘法, 目的在于找到与时间序列最相近的参数模型。通过调整协方差矩阵使得似然函数取得最大值, 即可得到与该时间序列最相近的噪声模型。假设观测值服从高斯正态分布, 最大似然函数可表示为[8, 9]:
| $ l{\rm{ }}\left( {\mathit{\boldsymbol{\hat v}}, \mathit{\boldsymbol{C}}} \right){\rm{ }} = \frac{1}{{{{\left( {2{\rm{ \mathit{ π} }}} \right)}^{N/2}}{{({\rm{det}}\mathit{\boldsymbol{C}})}^{1/2}}}}{\rm{exp}}(-0.5\mathit{\boldsymbol{\hat v}}{^{\rm{T}}}\mathit{\boldsymbol{C}}{^{-1}}\mathit{\boldsymbol{\hat v}}) $ | (4) |
式中, det是矩阵的行列式; C是假定噪声的协方差阵; N是时间序列的长度;
| $ {\rm{ln}}\left[{l\left( {\mathit{\boldsymbol{\hat v}}, \mathit{\boldsymbol{C}}} \right)} \right]{\rm{ }} = - \frac{1}{2}[{\rm{ln}}\left( {{\rm{det}}\mathit{\boldsymbol{C}}} \right){\rm{ }} + {{\mathit{\boldsymbol{\hat v}}}^{\rm{T}}}\mathit{\boldsymbol{C}}{^{-1}}\mathit{\boldsymbol{\hat v}} + N{\rm{ln}}(2{\rm{ \mathit{ π} }})] $ | (5) |
协方差矩阵C可以表达若干随机噪声过程, 如白噪声(WH)、可变白噪声(VW)、闪烁噪声(FN)、随机游走噪声(RW)、幂律噪声(PL)、一阶高斯马尔科夫噪声(GM)等, 以及它们之间的各类组合[1]。
频谱分析需要数据均匀采样, 且依赖于频谱平均, 无法使用最长时段的时间序列数据辅助估计频谱成分。最大似然估计法可以同时估计噪声类型、周期性振幅、测站速度及不确定度, 并且可以避开频谱分析的以上局限, 被认为是目前最准确的噪声分析方法[10, 11]。
2 时间序列分析软件CATSCATS[12]是由Williams设计开发的独立C程序, 是比较连续GPS坐标时间序列中随机噪声过程的软件。CATS软件的运行分为两个步骤:①使用最小二乘法计算式(1)中的线性部分的参数, 包括截距、斜率、偏移以及周期项的振幅; ②利用线性计算后的残差求得特定噪声模型的参数及振幅大小。
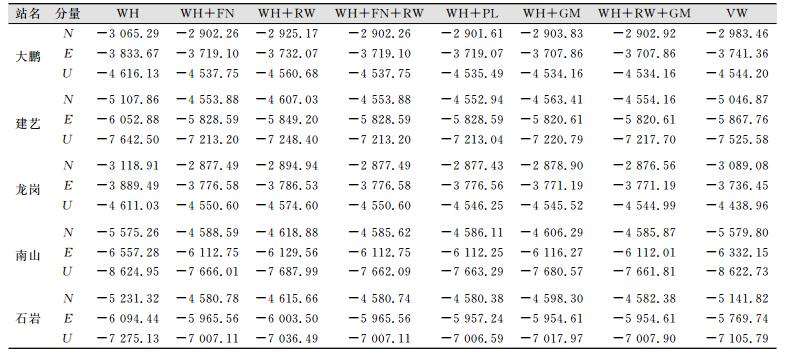
2.1 计算各参考站MLE值由于各参考站所处环境不同, 产生噪声的来源可能有会差异, 其噪声特性可能也不完全相同。同时考虑到测站变化的周期性特征, 有色噪声的确定性以及GPS技术中可能存在的高斯马尔科夫随机误差[10], 本文选取WH、WH+FN、WH+RW、WH+FN+RW、WH+PL、WH+GM、WH+RW+GM、VW共8种噪声模型, 下面采用CATS软件计算5个参考站各类噪声模型组合的最大似然估计值, 计算结果如表 1所示。
| 表 1 深圳CORS各参考站MLE值 Tab.1 MLE Values of Shenzhen CORS Stations |
 |
2.2 确定最优噪声模型
根据式(5)可得到不同噪声模型组合的极大似然对数值, 数值越大, 结果越可靠。蒙特卡罗模拟实验表明, 当两种模型的MLE之差δML>3.0时, 两种模型具有可区分性(95%的显著水平)[1, 13]。图 3给出了WH模型与其他7种模型之间的平均δML值, 即各参考站其他7种模型与WH模型差值的平均值。
 |
| 图 3 WH模型与其他7种模型之间的平均δML值 Fig.3 Average δML Values with Respect to the WH Model |
从图 3可以看出, MLE值最大的4种噪声模型从大到小是WH+RW+GM、WH+PL、WH+FN和WH+FN+RW, 且WH+PL、WH+FN和WH+FN+RW模型的MLE值之差δML < 3.0, 可区分度较低。同时, 为了确保结果的可靠性, 不能简单地以MLE值的大小作为最优噪声模型取舍的标准。当噪声模型包含的未知参数越多, 其MLE值也往往越大。本文选用Langbein等提出的保守估计准则判断不同模型的优劣[9, 14]。首先, 计算假设WN+FN组合模型的MLE值=0;然后, 依次将其余各类模型组合的MLE值分别与0假设作比较, 如果MLE差值大于设定的阈值, 则拒绝0假设, 认为该模型最优, 否则接受零假设。本文中将接受WH+PL模型的阈值设为0, 接受WH+RW+GM、WH+FN+RW模型的阈值设为2.6。
经统计, WH+PL为最优噪声模型组合。尽管如此, 基于以下几点原因, 本文仍采用WH+FN作为最优模型。①WH+FN与WH+PL的MLE均值之差δML=1.56, 可区分度很低, 两种模型都可以较好地表达本文中坐标时间序列的噪声特性; ②闪烁噪声FN是谱指数为-1的幂律噪声, 而幂律噪声PL求出的各参考站分量的非整数谱指数接近于-1, 如表 2所示; ③若采用WH+PL模型作为最优, 会造成各参考站谱指数不统一, 且随着时间序列长度的增加, 谱指数也会相应改变, 这为研究小范围区域参考站的噪声特性带来不必要的麻烦。因此, 选择WH+FN模型作为最优, 虽然保守一些, 但可靠性较强。
| 表 2 各参考站的谱指数 Tab.2 Spectrum Index of CORS Stations |
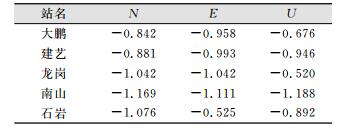 |
另外, 表 2中谱指数的最小值是南山站的垂直分量, 且该站水平分量的谱指数也均小于-1。在南山站建成的十余年来, 其周边的建筑物明显增多, 可能正是由于周围地表载荷增大导致地表逐渐变形, 进而对该站点位坐标尤其是垂直分量造成影响, 在坐标时间序列中表现为一定量的随机游走噪声。
3 结束语本文基于深圳CORS站观测数据, 求得参考站坐标时间序列, 在此基础上利用CATS软件求出多组噪声模型的MLE值, 运用保守估计准则判断出最优噪声模型为WH+FN, 并从地表负载的角度解释了南山站坐标时间序列中有存在随机游走噪声的可能性。下一步的方向是研究各种地球物理现象对基准站位置的影响规律, 并对各种误差模型进行修改, 进一步提高参考站位置精度。
本文中也存在一定不足之处。在确定参考站最优模型时, 本文利用5个参考站的δML均值做整体判断, 并没有逐个测站确定最优模型然后进行数学统计。主要原因是测站数目较少, 得出的统计结果将会包含较大的偶然误差。今后10个参考基站全投入使用, 数据将更精准可靠。
致谢
深圳市地籍测绘大队提供了CORS站6年观测数据, IGS组织提供了精密星历和钟差, Williams博士提供了CATS软件及软件使用手册和相关论文, 表示衷心的感谢!
| [1] |
袁林果, 丁晓利, 陈武, 等. 香港GPS基准站坐标序列特征分析[J]. 地球物理学报, 2008, 51(5): 1 372-1 384. |
| [2] |
Mao Ailin, Harrison C G A, Dixon T H. Niose in GPS Coordinate Time Series[J]. Journal of Geophysical Research:Solid Earth, 1999, 104(B2): 2 797-2 816. DOI:10.1029/1998JB900033 |
| [3] |
韩英, 符养. GPS高程数据时间序列分析[J]. 武汉大学学报·信息科学版, 2003, 28(4): 425-428. |
| [4] |
乔学军, 王琪, 吴云, 等. 中国大陆GPS基准站的时间序列特征[J]. 武汉大学学报·信息科学版, 2003, 28(4): 413-416. |
| [5] |
徐北海, 徐旭, 刘淑官, 等. 时间序列分析方法在变形数据处理中的应用研究[J]. 测绘地理信息, 2016, 41(1): 61-64. |
| [6] |
Nikolaidis R. Observation of Geodetic and Seismic Deformation with the Global Positioning System[J]. Cancer Research, 2002, 71(8): 714. |
| [7] |
黄立人. GPS基准站坐标分量时间序列的噪声特性分析[J]. 大地测量与地球动力学, 2006, 26(2): 31-33. |
| [8] |
Langbein J. Noise in Two-Color Electronic Distance Meter Measurements Revisited[J]. Journal of Geophysical Research:Solid Earth, 2004, 109(B4): 1-16. |
| [9] |
Williams S, Bock Y, Fang P, et al. Error Analysis of Continuous GPS Position Time Series[J]. Journal of Geophysical Research:Solid Earth, 2004, 109(B3): 412-430. |
| [10] |
李昭, 姜卫平, 刘鸿飞, 等. 中国区域IGS基准站坐标时间序列噪声模型建立与分析[J]. 测绘学报, 2012, 41(4): 496-503. |
| [11] |
Zhang J, Bock Y, Johnson H, et al. Southern California Permanent Geodetic Array:Error Analysis of Daily Position Estimates and Site Velocities[J]. Journal of Geophysical Research:Solid Earth, 1997, 102(B8): 18 035-18 055. DOI:10.1029/97JB01380 |
| [12] |
Williams S D P. CATS:GPS Coordinate Time Series Analysis Software[J]. GPS Solutions, 2008, 12(2): 147-153. DOI:10.1007/s10291-007-0086-4 |
| [13] |
Chen Wu, Gao Shan, Hu Congwei, et al. Effects of Ionospheric Disturbances on GPS Observation in Low Latitude Area[J]. GPS Solutions, 2008, 12(1): 33-41. DOI:10.1007/s10291-007-0062-z |
| [14] |
Langbein J. Noise in GPS Displacement Measurements from Southern California and Southern Nevada[J]. Journal of Geophysical Research:Solid Earth, 2008, 113(B5): 1-12. |
 2018, Vol. 43
2018, Vol. 43


